浅谈学生数学错解的成因及对策

☉江苏省江浦高级中学 徐爱勇

一、问题的提出

根据布鲁纳的认识发展理论，学习本身是一种认知过程.在这个过程中，个体的学习总是要通过已知的内部认识结构，对输入信息进行整理加工，以一种易于掌握的形式加以存储.也就是说，学生能从原有的知识结构中提取最有效的旧知识帮助吸纳新知识.这样，新旧知识在学生的头脑中发生积极的相互作用和联系，导致原有知识结构的不断分化和重新组合，使学生获得新知识.但是，这个过程并非总是一次性成功的，需要通过不断的练习来完成.

数学学科的特点决定学生学习知识不是简单地吸收，而是通过思维活动把前人的成果转化为自己的思维结果.这个转化称为“建构”.知识建构，是靠不断主动修正错误，并能在新环境中解决新问题.而学生在学习数学的过程中，势必要做一定量的习题.这是一项长期的系统工程，在这个系统中一个重要的环节就是对数学错解的开发和利用.一个显然的事实，我们对待数学错解的态度直接决定着学生数学思维能力发展的走向.

为此，本文力图对“学生数学错解”的成因进行一些会诊，并给出相应的一些对策.从而期望能够达到改变我们的教学方法，提高课堂教学效率，启迪学生的数学思维，最终达到优化学生思维品质的目的.

二、成因及对策

症状1——不良学习习惯的影响

学生的不良学习习惯是造成学生把题做错的一个重要原因.具体地说，主要有以下方面：不认真审题；做完题后不检查；解答表述不规范，只写计算结果不写计算过程；计算粗心大意等.而这些不良的学习习惯就是“会而不对，对而不全”的根源.在教学和学习过程中，学生经常遇到这种情况：对一些习题或考试试题自己完全会解答，但做完或考试结束后总会丢失一些分，教师感到惋惜，自己也深感遗憾.教师在评讲试题错误时虽指出了错误原因，但由于不良习惯的影响，下次遇到同类问题时学生仍然出现相同的错误.

错解：很多学生在解答此题时，第一反应便是设直线l的方程为y=k（x-2），从而较快地求出方程为3x-4y-6=0.

成因：他们所犯的错误是忽略了题目“直线l过点P（2，0）”这一条件，与所设直线l的方程为“y=k（x-2）”这一形式之间的相互推出关系，造成解答不完整的主要原因是未认真审题.如果认真审题就会发现所设直线方程的局限性，也就不会犯以上错误.但由于没有养成认真审题的良好习惯，虽然教师评讲后当时也知道，但下次遇到同一问题仍然会看到题时马上凭直观感知就仅仅设直线方程的“点斜式”（若是在考场中为了抓紧时间更会是这样），从而又重复地出现犯过的错误.

对策：（1）“找对象”，我们可以把各个知识板块中类似的问题进行“合并同类项”，如：

①若关于x的方程kx2-（2k-1）x+k=0有实数根，则实数k的取值范围为________.

②已知集合P={x|x2+x-6=0}，Q={x|mx-1=0}，若P∩Q=Q，则满足条件的实数m所组成的集合为________.

③已知数列{an}的前n项和Sn=n2+n+2，则an=________.

④动点P到A（1，1）和直线x+2y=3的距离相等，则点P的轨迹方程为________.

从而，使学生对这类错误能够形成较系统的认识，最终达到从“通过题目找问题”到“通过问题找题目”的跨越.

（2）“写提醒”，如：贴标签，注意认真审题！条件是否漏掉！计算仔细些！…把这些激励和督促自己的口头语言转换成书面语言，贴在文具盒、书桌的右上角、床头等，以便于在以后的考试中加强提醒.

（3）“做比赛”，如利用研究性学习课，把班级的同学分成几个小组，轮流由学生自主对此类问题进行考查，做到常抓不懈.

症状2——原有思维定势的影响

思维定势是指已有的思维活动经验在反复使用中所形成的比较稳定的、定型化了的思维路线、方式、程序和模式（在感性认识阶段也称作“刻板印象”）.当解决某一问题的思维定势一旦形成，就会在见到类似情景时自觉地运用原有思维方式进行思考与解决问题.思维定势有积极的和消极的.积极定势可以促进问题的快速解决，消极定势则会阻碍人们对新问题的解决.在学生学习中消极的思维定势则会对新的学习产生干扰.

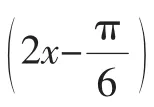
成因：本题错解的原因是对三角函数“依图识性”把握不够到位.究其原因，是由于从y=sinx与y=cosx的图像的对称中心点的结论产生了负迁移，故而产生了错解.

（2）“进一步”，再引导学生对一个具有对称中心的函数，从代数的角度提炼其规律.（预设：学生不难发现，函数图像的对称中心未必在函数图像上.）

（3）“回头看”，最后还引导学生反思解题过程中犯错的节点所在，力图把消极的思维定势转化为积极的思维定势.从而，加深对概念的深层次的理解，最终达到准确把握概念的实质，做到真正地理解.

症状3——整体意识缺乏的影响

在解题过程中，要随时注意整体与局部的关系，不能以局部的性质代替整体，从而，避免错误发生.

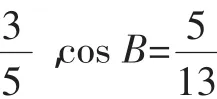
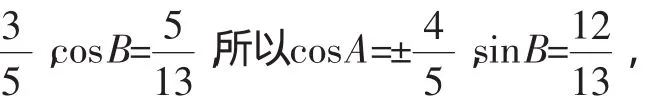
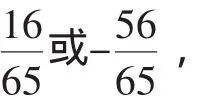
为了避免此类错误的发生，我们应该帮助学生树立整体的思想，即在一次整体变换过程中，确保变换的各个部分应该是和谐共存的.

对策：（1）“摆擂台”，我们在讲评时可以把错误的解法和正确的解法虚拟地转化为同学甲和同学乙的解答过程，并用实物投影展示出来，从而引起学生思维上强烈的碰撞.

（2）“找代言”，我们引导学生进行讨论辨析，因势利导地设置一些问题，使学生通过分析、诊断，尽可能地由学生自主提炼出代数变形过程中的一些注意点.

（3）“寻变式”，解决完此题后，我们可以带领学生做如下变式，以加深其体会.

变式3：已知函数f（x）=x3+ax2+bx+a2在x=1处有极值10，则实数a，b的值分别为________.

症状4——符号理解不全的影响

数学问题的表达中往往充满着许多数学符号，解决它需要学生具有较强的抽象思维能力.若对抽象的数学符号所表示的意义理解不够深刻，很容易导致错解的发生.

案例4：已知f（x）=2+log3x，x∈［1，9］，求函数y=［f（x）］2+f（x2）的值域.

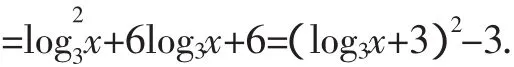
又因为x∈［1，9］，所以log3x∈［0，2］，

所以y=（log3x+3）2-3在log3x∈［0，2］上单调递增，

所以6≤y≤22，即函数的值域为［6，22］.

成因：对于上述解答，不少学生认为是对的.但是，我们稍作分析，可以发现，虽然这里考虑到了函数的定义域，并由x∈［1，9］得到log3x∈［0，2］.但“x∈［1，9］”并不是函数y=［f（x）］2+f（x2），即y=（log3x+3）2-3的定义域，而是函数f（x）=2+log3x的定义域.因此，解答是错误的.从而，我们不难求出函数y=［f（x）］2+f（x2）的定义域为［1，3］，则值域为［6，13］.

对策：（1）“查字典”，引导同学们翻阅课本，找到教材中对“定义域”最原始的描述，即“回到定义中去”.

（2）“做记录”，数学学习过程中，出现这样的错误是难免的.但是，要提高学习效率，就必须减少重复错误的次数.做较为详细的记录，重复刺激的次数越多，痕迹越深，记忆效果就越好.

（3）“定期练”，根据心理学知识，在记忆的最初阶段，遗忘速度很快，后来逐渐减慢，相当长时间之后，几乎就不再遗忘.所以，定期的训练，就显得十分有必要.

三、结束语

辨析问题错解的原因，是想从根本上寻找错解的原因，认清什么是错误的，错在何处，为何产生这种错误，从而探索避免错误发生的对策以及解决问题的正确思路，提高解答数学问题的准确性；通过辨析，训练学生数学思维的严谨性、深刻性、灵活性、批判性与独创性，使学生的数学素养得到有效的提升.

1.王富英.“错误重复现象”产生的原因及消除对策.数学通报，2011（7）.

2.徐爱勇.数学错解中的定“性”分析.中学数学研究（广州），2012（5）.

3.王光明，杨蕊.数学学习中的“懂而不会”现象.中学数学教学参考，2012（10）.

4.李晓峰.建立成长题库：一种提高数学成绩的设想和方法.中学数学月刊，2012（11）.