考虑连接特性的子结构频响综合方法及实现
王 威 胡于进 凌 玲
华中科技大学,武汉,430074
0 引言
子结构综合方法在航天器设计、汽车NVH分析等复杂结构的动力学特性分析中有着广泛的应用。传统上把子结构综合方法分为两大类[1]:基于模态的子结构综合(component-modesynthesis,CMS)[2]和基于频响函数(frequencyresponse function,FRF)的子结构综合(FRF-basedsubstructuring,FBS)[3]。它们分别用于理论模型和试验模型的综合,而工程中通常存在混合模型的综合问题,即有限元建模的理论模型与试验测试获得的试验模型的综合[4]。混合模型的综合主要采用基于频响函数的综合,但基于频响函数的综合存在对整个子结构频响矩阵求逆运算的问题,这导致计算效率和精度不高[5]。Jetmundersen等[6]发展了一种子结构导纳综合方法(RC方法),计算时只需对连接部分的频响矩阵求逆,使计算精度和效率得到较大提高,但该方法仅适用于两个独立子结构之间的综合。Ren等[7]在此基础上发展出一种多子结构综合方法即GRC(generalizedreceptancecoupling)方法,能够得到非独立子结构之间的综合。值得指出的是,GRC方法只考虑了刚性连接特性的处理,而工程实际中结构的连接基本都是柔性连接,为此,Liu等[8]提出了一种考虑弹性连接介质的综合方法,但该方法实质上是把连接件当作一个子结构进行处理,连接件与被连接件之间仍为刚性连接,未将连接参数从子结构系统中独立出来,不便于使用和实际操作。对于一些常用的连接模型,如弹簧连接、轴套连接等,如何用特征参数来表达其连接刚度和阻尼等信息,使其与子结构完全独立,具有更明确的物理意义是一个有意义的研究课题。因此,本文以GRC方法为基础,用统一的参数模型来实现连接部分的独立化、模块化处理,使子结构之间的连接不再局限于刚性连接,实现了刚性连接和柔性连接的统一。同时,基于所提出方法,研发了多子结构混合建模及综合求解系统。
1 基于频响的子结构综合方法
在GRC方法中,子结构系统的定义为

通过引入刚性连接条件,得到整体结构的频响矩阵:

式中,下标n、j分别表示综合后整体结构的内部自由度和界面自由度。
该方法在计算过程中涉及矩阵求逆,但只需对连接处的频响矩阵求逆。采用奇异值分解方法(SVD)求逆[9],可以有效降低测试误差对综合结果的影响。
2 考虑参数化连接特性的子结构频响综合方法
2.1 子结构之间的连接模型
参数化的连接模型是指一些常用的连接,如弹簧连接、轴套连接、螺栓连接等,其连接特性可以用刚度和阻尼表示。对于柔性连接,传统上两个子结构间的连接可以用弹性元件和阻尼元件来模拟[10],即每个连接自由度都用一个等效刚度和等效阻尼来表示其连接特性,如图1所示。
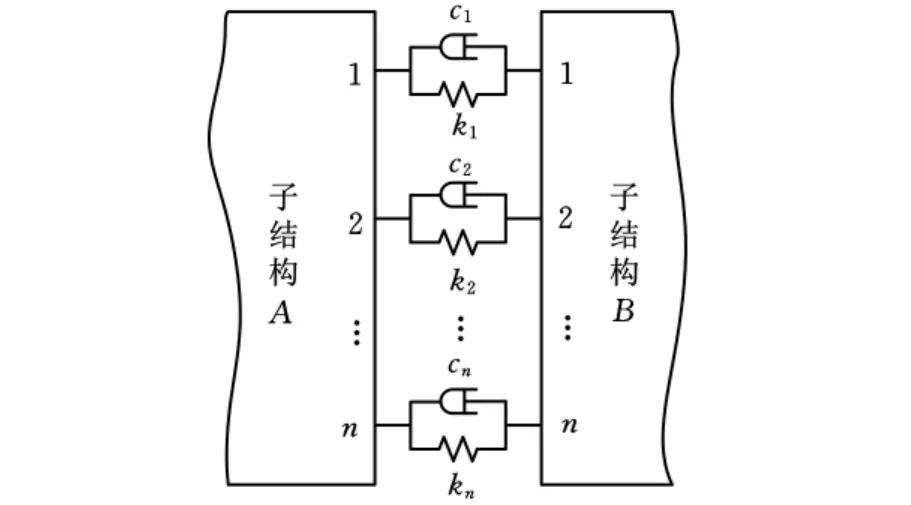
图1 柔性连接模型
根据连接部件的力平衡条件,子结构A和B在连接处界面自由度的振动位移和作用力满足如下关系:
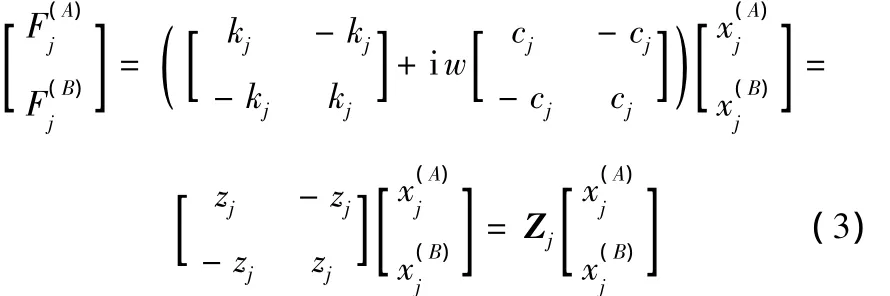


其中,ZC为连接部分的n×n阶阻抗矩阵,ZC=[zij]n×n,矩阵 ZC中的任一项zij为连接阻抗,其物理意义为第i个连接自由度产生单位位移时第j个连接自由度上需要施加的作用力。当不同连接自由度之间没有耦合项时,ZC可以化为对角阵。
2.2 引入连接后的子结构综合
简单起见,用b'、c'表示连接部件的界面自由度,用a、b和c表示连接后综合结构的自由度。原有子结构系统位移和力之间的关系如下:

根据式(4)的推论,连接处的阻抗矩阵计算公式为
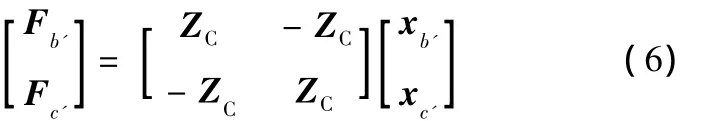
引入连接处的位移协调和力平衡条件:

将式(5)~式(7)联立,可得

将式(8)代入式(9),得

将式(5)~(8)式联立,得

将式(10)代入式(11),可得综合结构的频响函数矩阵:
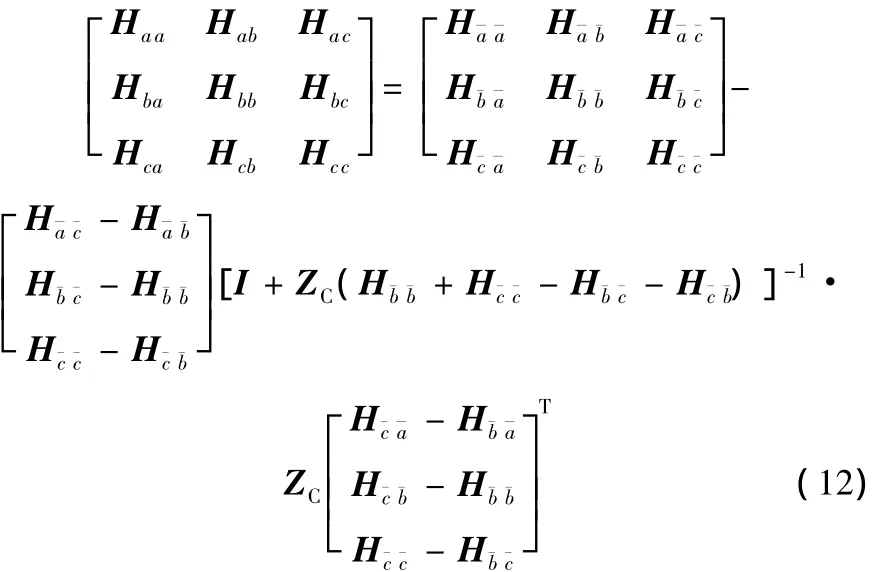
从式(12)提取出中间项,可以证明得到

将式(13)代入式(12),得到最终的综合结果:
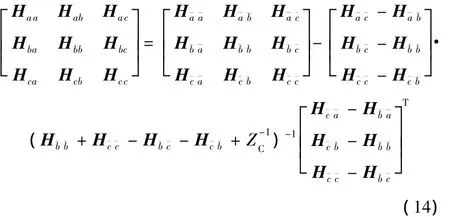
将式(14)与式(2)相比可以发现,二者在形式上相似,但式(14)的中间项在求逆时引入了连接处部件的阻抗矩阵。根据2.1节中子结构之间的连接模型,当连接点之间的刚度趋向于无穷大时,Z-1C趋向于零矩阵,退化为刚性连接。式(14)很好地实现了刚性连接和柔性连接的统一处理,且矩阵求逆的阶次并未增加,可以应用于不同连接类型的子结构综合。
3 考虑连接特性的子结构频响综合方法实现
本文要实现的是多子结构(包括试验模型和理论模型)在不同连接特性下的混合综合,系统结构可以按照功能划分为输入模块、预处理模块、综合计算模块和后处理模块,实现流程如图2所示。
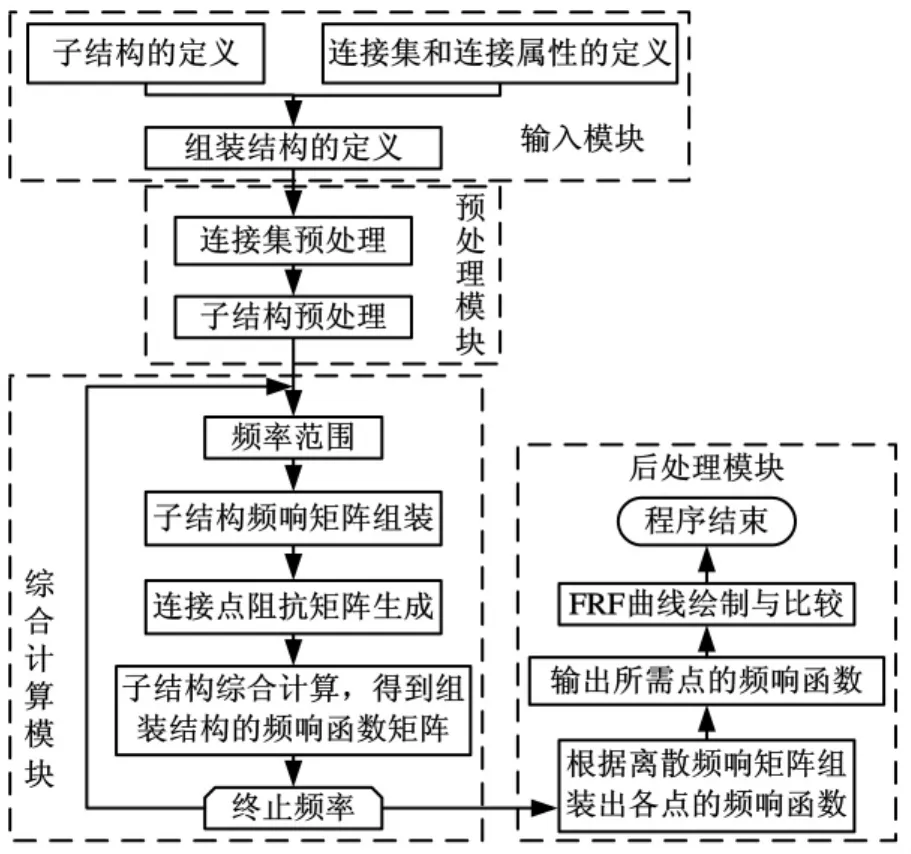
图2 子结构频响综合整体流程
3.1 输入模块
输入模块包括以下三个部分:
(1)子结构的定义。子结构分为试验子结构和理论子结构。试验子结构用试验得到的激励点和响应点之间的频响函数数据表示,理论子结构用有限元计算得到的模态或频响数据表示。子结构的定义如图3所示。

图3 子结构定义模块
(2)连接集和连接属性的定义。连接集用来定义子结构之间需要连接的节点编号和自由度。定义连接属性时,需要预设不同的连接方式(刚性连接、弹簧连接、动刚度连接等),定义不同自由度之间的连接刚度和阻尼,为后续的连接阻抗计算做准备。
(3)组装结构的定义。定义完所有的子结构、连接集和连接属性之后,根据计算要求将其引入相应的组装结构中,就完成了组装结构的定义,可以进行后续的处理和计算。
3.2 预处理模块
预处理模块包括连接集的预处理和子结构的预处理。连接集的预处理主要用于调整个子结构频响矩阵的生成顺序,为后续子结构系统的整体频响矩阵组装和结果矩阵中各频响函数的定位做准备。
对子结构的预处理包括试验子结构的预处理和理论子结构的预处理。子结构预处理的目的是为了得到各个子结构在各离散频率点的频响函数矩阵,其预处理流程如图4所示。

图4 子结构预处理模块
在理论子结构的预处理中,按照传统的模态分析理论,可以根据结构模态信息计算得到频响函数矩阵[12]。由于计算过程涉及多重循环,运算次数较多,在程序的内层循环中用向量运算代替浮点数之间的乘法运算,同时,将运算过程中的中间变量存储下来,以空间换时间,运算效率可以显著提高。
3.3 综合计算模块
由于实验测试和理论计算所得的频响函数数据通常是一系列离散频率点的响应值。同时,考虑到连接特性一般都含与频率相关的阻尼项,因此,在综合过程中,连接特性的阻抗矩阵计算和组装结构的综合计算都必须在各自离散的频率点进行。综合计算模块具体过程由以下三个步骤来实现:
(1)子结构系统频响矩阵的组装。子结构系统整体频响矩阵的组装是一个繁琐而复杂的工作,首先需要对每个子结构按照内部节点集和连接点集进行分块取值。分块完毕后,在子结构系统频响矩阵中,对所有子结构的所有分块矩阵进行定位和组装,最终形成式(1)的形式。
(2)连接部分阻抗矩阵的生成。在已定义的连接集和连接属性中,根据预设的连接模型计算方法得到各连接自由度之间的连接阻抗。然后,按照连接点顺序将其组装成矩阵,即可得到离散频率处的阻抗矩阵。
(3)子结构频响综合计算。用式(14)进行理论计算。在式(14)中,需要对中间矩阵求逆,还要进行数次矩阵乘法运算,这样的过程需要在每个离散频率点进行,矩阵运算的次数将会很多。为了提高计算效率,在具体实现过程中,本文采用了Intel MKL数学计算库,并用奇异值分解对矩阵求逆,提高了运算结果的可靠性。
3.4 后处理模块
后处理模块主要从综合计算所得的离散频响矩阵序列中组装形成不同激励点和响应点之间的频响函数,并对每个频响函数进行定位,然后,根据需求进行幅值、相位等处理,输出幅频、相频曲线。
4 算例研究
4.1 模型描述
图5所示模型为Esfandiari等[13]提供的一个桁架模型,本文将该桁架结构分为两个子结构,子结构之间用柔性连接处理。子结构1左端铰接,子结构2右端简支。所用杆单元的材料为钢,弹性模量为20GPa,各杆的截面面积列于表1。子结构1和子结构2 的连接对为(1,8)、(7,11),分别在X和Y方向用弹性单元连接,连接刚度为108N/m。

图5 子结构及组合结构有限元模型

表1 桁架中各杆的截面面积
4.2 计算结果分析
首先建立子结构1和子结构2的有限元模型,得到模态计算结果。将两个子结构按照柔性连接进行理论子结构之间的频响综合,计算得到节点10X方向的激励和响应的频响函数(在频响计算中,通常用节点编号加自由度方向表示激励和响应)。将子结构综合结果与整体模型频响计算结果比较,幅频曲线如图6所示。从图6可以看出,子结构频响综合结果与整体结构频响计算结果几乎完全一致,说明该方法有效。
我们通过对子结构1计算得到的频响函数分别施加5%和10%的随机误差(用来模拟试验数据)。子结构2仍然采用理论模态结果计算得到精确的频响函数。沿用之前的柔性连接条件,计算得到模拟试验模型和理论模型的频响综合结果,并与整体结构的频响函数比较,观察综合结果对误差的敏感性。图7、图8分别表示子结构1的频响数据施加5%和10%的随机误差后的综合结果。通过对图7、图8的比较可知,随着模拟试验数据随机误差的增大,综合结果与整体结果之间的误差也会增大,但二者的整体趋势仍然保持一致。说明当试验误差不是太大的时候,该方法在处理试验数据和理论模态混合综合方面有效。
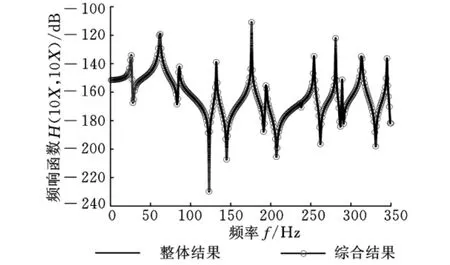
图6 理论子结构综合结果

图7 引入5%随机误差后的混合综合结果

图8 引入10%随机误差后的综合结果
5 结语
本文在GRC方法基础上,引入了子结构之间参数化的连接特性,实现了子结构频响综合过程中刚性连接和弹性连接的统一处理,且矩阵求逆的阶次并未增加,可以应用于不同连接类型的子结构综合。同时,实现了试验子结构和理论子结构的统一处理,即混合建模,并开发出相应的混合建模求解系统。数值计算表明,在模拟试验数据加入一定随机误差的情况下,综合结果与整体结果也有较好的适应度。
[1]Cuppens K,Sas P,Hermans L.Evaluation of the FRF Based Substructuring and Modal Synthesis Technique Applied to Vehicle FE Data[C]//Proceedings of the International Conference on Noise and Vibration Engineering.Leuven,Belgium,2002:1143-1150.
[2]Heylen W,Lammens S,Sas P.Modal Analysis Theory and Testing[M].Leuven,Belgium:Katholieke Universiteit,1998.
[3]吴仕超,蔡国平.考虑界面转角自由度的频域子结构法研究[J].振动工程学报,2011,24(3):323-326.
Wu Shichao,Cai Guoping.FRF Based Substructuring Technique Considering Rotational Degrees of Freedom of Interface[J].Journal of Vibration Engineering,2011,24(3):323-326.
[4]董兴建,孟光.实验模型和有限元模型的混合建模方法[J].振动与冲击,2009,28(7):38-72.
Dong Xingjian,Meng Guang.A Free - interface Component Mode Synthesis Method Based on Residual Dynamic Flexibility[J].Journal of Vibration and Shock,2009,28(7):38-72.
[5]Imergun M,Robb D A,Ewins D J.Structural Modification and Coupling Dynamic Analysis Using Measured FRF Data[C]//Proceedings of the 4th International Modal Analysis Conference.London,1987:1136-1141.
[6]Jetmunderson B, Bielawa R L, Flannelly R.Generalized Frequency Domain Substructure Synthesis[J].Journal of the American Helicopter Society,1988,33(1):55-64.
[7]Ren Y,Beards C F.On Substructure Synthesis with FRF Data[J].Journal of Sound and Vibration,1995,185(5):845-866.
[8]Liu W,Ewins D J.Substructure Synthesis via Elastic Media[J].Journal of Sound and Vibration,2002,257(2):361-379.
[9]Tsai J S,Chou Y F.The Identification of Dynamic Characteristics of a Single Bolt Joint[J].Journal of Sound and Vibration,1988,125(3):487-502.
[10]廖伯瑜,周新民,尹志宏.现代机械动力学及其工程应用[M].北京:机械工业出版社,2003.
[11]Mao Kuanmin,Li Bin,Wu Jun,et al.Stiffness Influential Factors-based Dynamic Modeling and Its Parameter Identification Method of Fixed Joints in Machine Tools[J].International Journal of Machine Tools & Manufacture,2010,50:156-164.
[12]李德葆,陆秋海.试验模态分析及应用[M].北京:科学出版社,2001.
[13]Esfandiari A,Bakhtiari- Nejad F,Sanayei M,et al.Structural Finite Element Model Updating Using Transfer Function Data[J].Computers and Structures,2010,88:54-64.

