直梁圆角型柔性铰链的回转精度分析
赵 磊 巩 岩
中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室,长春,130033
0 引言
柔性铰链利用其自身的弹性变形而非刚性元件的运动来传递或转换运动、力或能量,相对于传统运动铰链,具有运动分辨率高、无摩擦、无需润滑、制造工艺简单等优点,广泛应用于光刻物镜[1-4]、微动工作台[5-8]、电子扫描显微镜[9]、超精密加工机床[10-12]等领域。
理想铰链转动时,其转动中心是固定不动的,而柔性铰链依靠自身弹性变形产生运动,其转动中心随着载荷变化而移动,因此会引起转动误差。其转动误差可以通过柔性铰链几何中心的偏移量表示。国内外学者围绕柔性铰链的精度进行了相关研究工作。文献[13-14]基于卡氏第一、第二定理建立了圆弧型、椭圆型、抛物线型、双曲线型以及直梁圆角型柔性铰链回转精度的理论模型,但其模型中没有考虑剪切引起的应变能。文献[15]同样基于卡氏第一、第二定理给出了直梁圆角型、抛物线型以及正割曲线型柔性铰链回转精度的解析计算公式,但其推导过程中同样没有考虑剪切引起的应变能的影响。文献[16]采用有限元法分析了圆弧型、直梁圆角型和椭圆型柔性铰链的回转精度,结果表明:当铰链的长度、宽度和最小厚度相等,且施加的外载荷和铰链偏转相同时,直梁圆角型柔性铰链相对回转精度最高。文献[17]分析了加工误差对柔性铰链精度的影响。
上述针对柔性铰链回转精度的分析大都是基于卡氏第一、第二定理采用能量法进行的推导,本文则根据材料力学悬臂梁理论,在考虑轴向拉伸、弯曲和剪切等作用下,针对直梁圆角型柔性铰链的回转精度进行了分析。首先,基于悬臂梁理论推导了柔性铰链几何中心平面内线性变形量Δx、Δy的解析计算方法,建立了柔性铰链回转精度矩阵的闭环解析模型,并给出了当r≪t时回转精度矩阵各项参数的简化计算公式。然后,建立了直梁圆角型柔性铰链的有限元模型,通过比较解析值和有限元仿真值,验证了回转精度矩阵闭环解析模型的正确性。最后,分析了柔性铰链的材料参数和结构参数对其回转精度的影响。
1 直梁圆角型柔性铰链的回转精度
直梁圆角型柔性铰链如图1所示,铰链为直梁片状结构,两端与基体采用圆角方式连接。直梁圆角型柔性铰链的主要几何参数有铰链高度h、铰链长度l、铰链厚度t及圆角半径r。建模时将柔性铰链的右端固定,左端为自由端,x轴正方向从柔性铰链的固定端指向变形端,y轴垂直于直梁薄片平面。
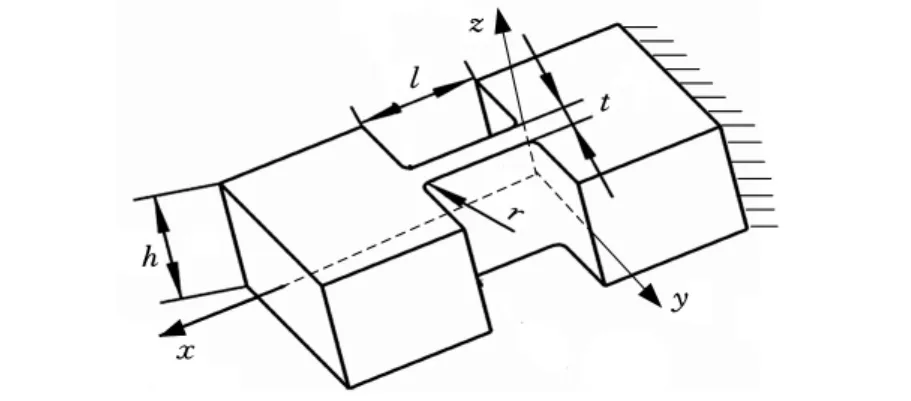
图1 直梁圆角型柔性铰链
图2所示为直梁圆角型柔性铰链的截面图。图中0-1段和3-4段为圆角部分,1-3段为直梁部分。直梁圆角型柔性铰链是厚度t随x变化的变截面梁,其函数表达式为

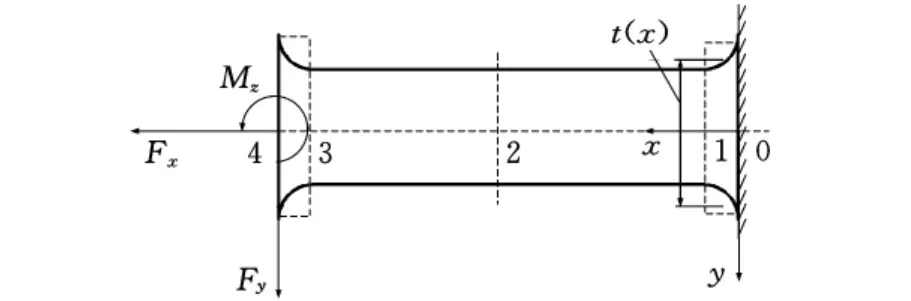
图2 直梁圆角型柔性铰链截面图
柔性铰链的回转精度是指在自由端4点处外载荷Fx、Fy、Mz作用下柔性铰链几何中心2点处的位姿变化量Δx、Δy。当柔性铰链的变形量较小时,可以认为其变形为线弹性变形,建模时应考虑轴向拉压、弯曲和剪切的影响。
1.1 Fx引起的x方向线性变形
柔性铰链几何中心2点处x方向的线性变形主要是由力Fx拉压引起的。
根据拉压胡克定律,得到0-1段变截面梁的轴向变形量为
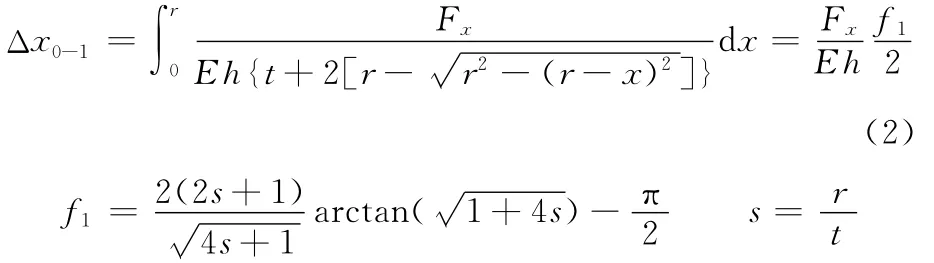
式中,E为柔性铰链材料的弹性模量。
根据拉压胡克定律,得到1-2段等截面梁的轴向变形量为

柔性铰链几何中心2点沿x轴方向的变形量为0-1段和1-2段变形量的总和,因此有
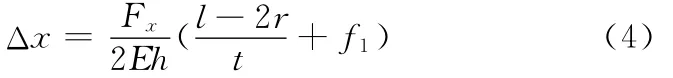
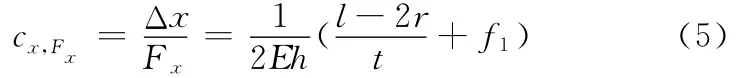
当r≪t时,式(4)、式(5)分别简化为

1.2 Fy引起的y方向线性变形
力Fy引起的沿y方向变形主要由弯矩变形和剪切变形组成。
Fy弯矩引起的0-1段变截面梁沿y方向的变形量为

Fy弯矩引起的1-2段等截面梁沿y方向的变形量为
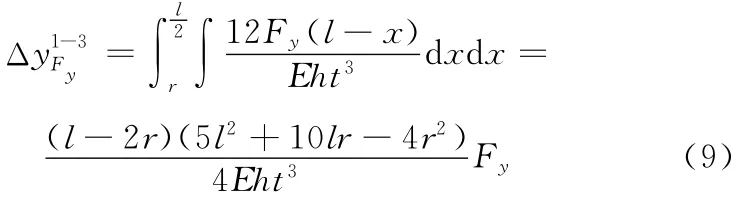
Fy剪切引起的0-1段变截面梁沿y方向的变形量为
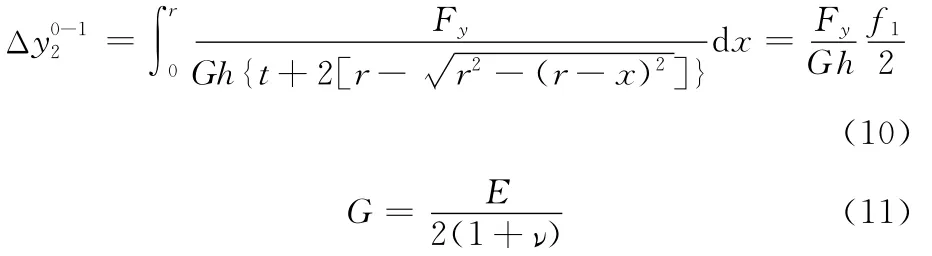
式中,G为柔性铰链材料的切变模量;ν为柔性铰链材料的泊松比。
Fy剪切引起的1-2段等截面梁沿y方向的变形量根据剪切胡克定律有
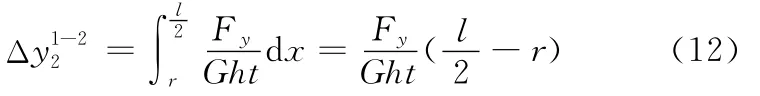
于是得到Fy作用下柔性铰链几何中心2点沿y方向的总变形量为
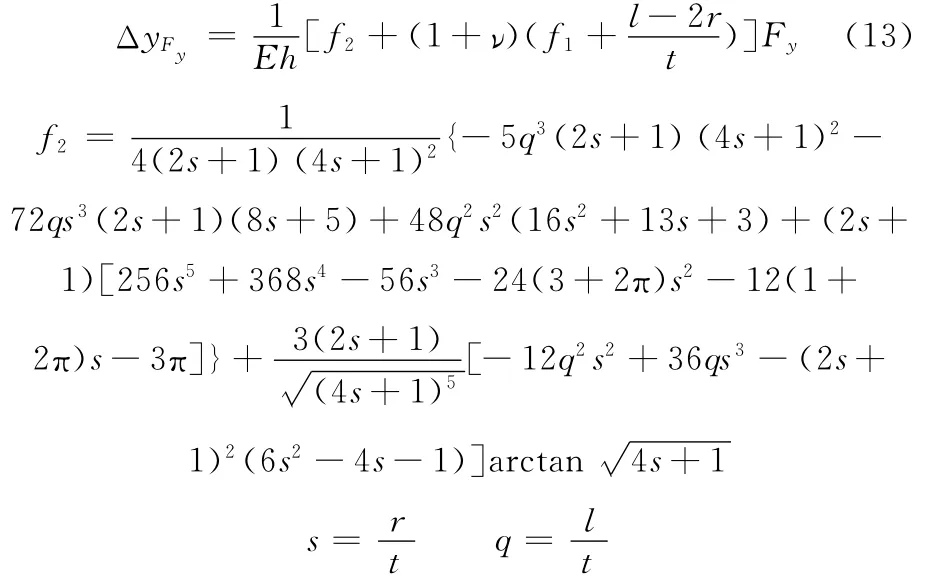
于是得到柔性铰链的回转精度矩阵参数为
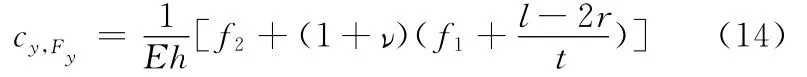
当r≪t时,式(13)、式(14)可简化为

1.3 Mz引起的y方向的线性变形
施加力矩Mz时,0-1段变截面梁沿y方向的变形量为

施加力矩Mz时,1-2段等截面梁沿y方向的变形量为

由Mz引起的沿y方向的变形量为0-1段、1-2段变形量的总和,因此有

于是得到柔性铰链的回转精度矩阵参数为
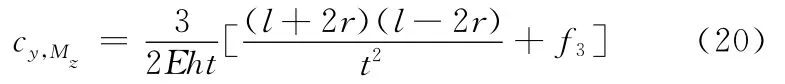
当r≪t时,式(19)、式(20)可简化为
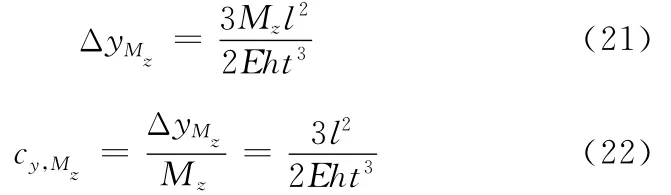
1.4 柔性铰链的回转精度矩阵闭环模型
根据式(5)、式(13)、式(20)可以得到直梁圆角型柔性铰链几何中心2点处平面内的偏移量Δx、Δy与平面内力/力矩Fx、Fy、Mz的关系,将公式转换成矩阵形式为
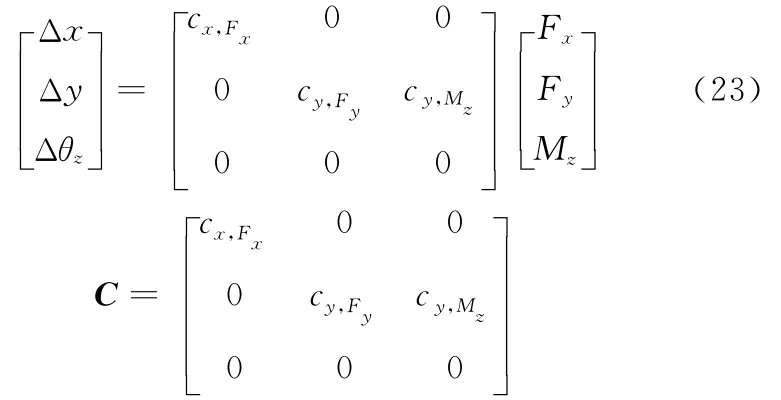
式中,C为柔性铰链平面内的回转精度矩阵。
2 直梁圆角型柔性铰链回转精度的有限元验证
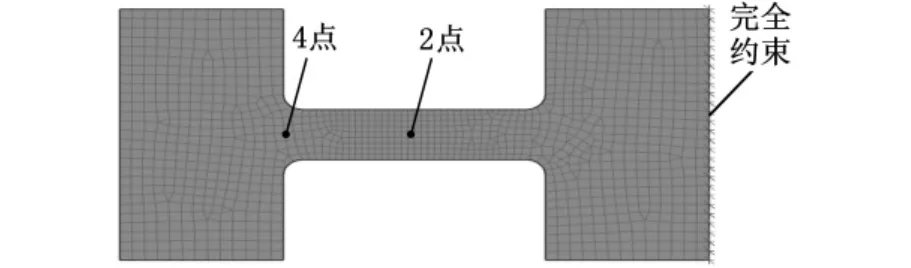
图3 直梁圆角型柔性铰链有限元模型
为了验证推导得到的直梁圆角型柔性铰链回转精度闭环解析式,采用UG NX NASTRAN软件对直梁圆角型柔性铰链进行了有限元建模仿真和分析。直梁圆角型柔性铰链的有限元模型如图3所示。柔性铰链的材料参数和结构参数分别为:弹性模量E=141GPa,泊松比ν=0.259,铰链高度h=11mm,铰链厚度t=1mm,铰链长度l=4mm,圆角半径r=0.3mm。建模时,柔性铰链的右端完全约束,在左侧的直梁自由端4点处施加单位力Fx、Fy和单位力矩Mz,观察柔性铰链几何中心2点的偏移量Δx、Δy。图4为单位力Fx、Fy和单位力矩Mz综合作用下的直梁圆角型柔性铰链的变形图,图中虚线所示为柔性铰链变形前的位置,由图可知施加单位载荷时,偏移量Δy远大于偏移量Δx。

图4 直梁圆角型柔性铰链仿真分析结果
回转精度矩阵各参数的有限元仿真分析结果与解析计算值如表1所示,两者的相对误差控制在5%以内,从而验证了直梁圆角型柔性铰链回转精度的闭环解析式的正确性。

表1 回转精度矩阵各参数的解析值与仿真值
3 材料参数和几何参数对柔性铰链回转精度的影响
柔性铰链的回转精度是通过其几何中心2点的偏移量来表示的,相同外载荷作用下,几何中心2点的偏移量越小,其回转精度就越高。为了便于分析,取加载到自由端4点的外载荷为单位力和单位力矩,于是式(23)可以表示为

由式(24)可知,柔性铰链回转精度与材料弹性模量E和泊松比ν有关系,其中,弹性模量E越大,回转精度越高;泊松比ν越大,回转精度越低;柔性铰链回转精度与铰链高度h成反比,即柔性铰链高度h越大时,其回转精度越高。
为了分析铰链厚度t、铰链长度l及圆角半径r对回转精度的影响,以及量纲一参数s和q对偏移量Δx、Δy的影响,假设s=r/t,q=l/t,且0≤s≤1,3≤q≤10,如图5所示。由图5可知,柔性铰链几何中心2点的偏移量Δx随着s的增大而近似线性减小,随着q的增大而线性增大;Δy随着s的增大而非线性减小,随着q的增大而非线性增大。因此,当柔性铰链的厚度t确定时,圆角半径r越大,铰链长度l越小,其回转精度就越高。
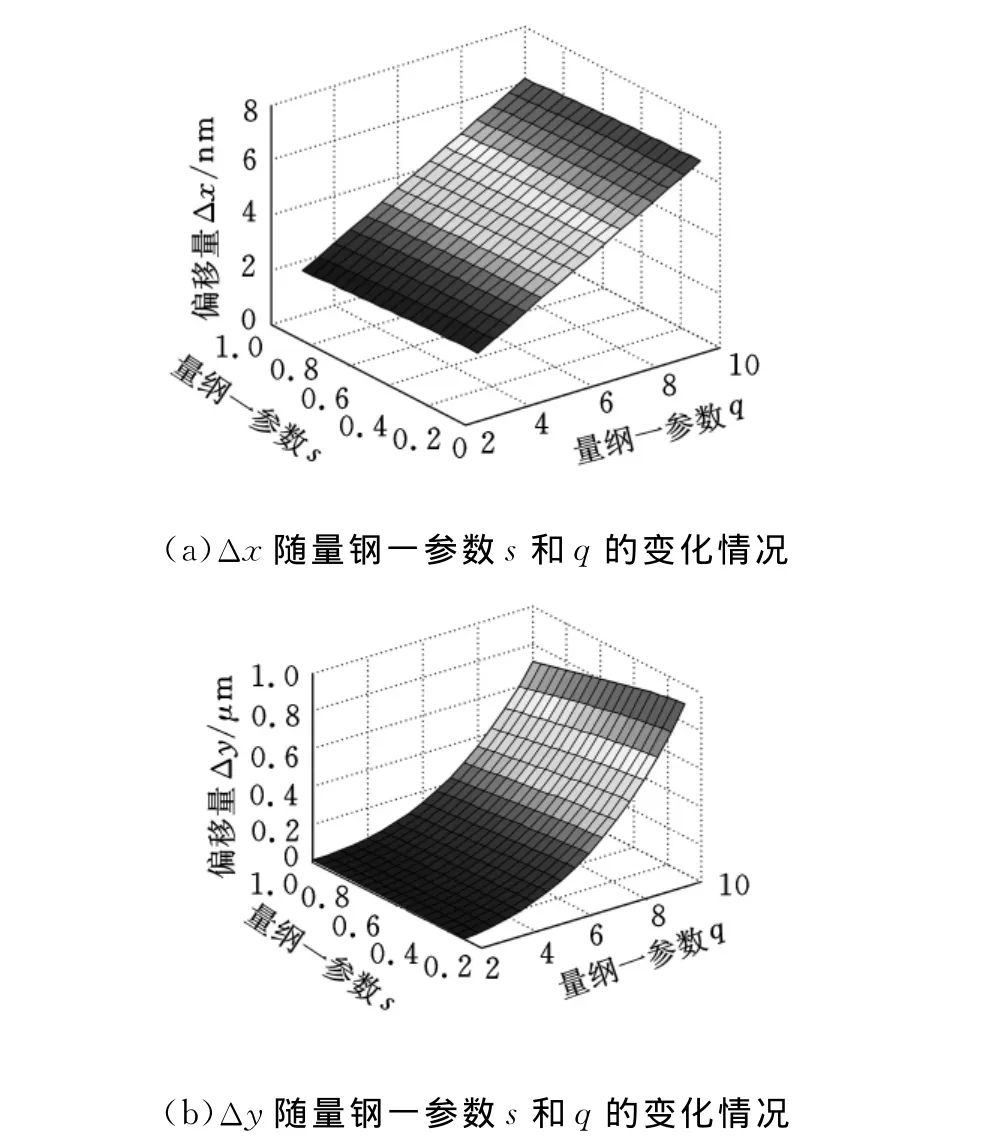
图5 回转精度随量钢一参数s和q的变化图
为了分析柔性铰链的厚度t对其回转精度的影响,若假定0.5mm≤t≤4mm,h=11mm,r=0.3mm,l=4mm,则Δx、Δy均随着t的增大而非线性减小,且其减小的速率均随着t的增大越来越小,如图6所示。
4 结论
本文基于悬臂梁理论推导了直梁圆角型柔性铰链几何中心点2的偏移量Δx、Δy的解析计算方法,建立了柔性铰链平面内回转精度矩阵的闭环解析模型,给出了r≪t时回转精度矩阵模型的简化计算公式。采用与有限元分析结果相比较的方式对解析模型进行了验证,结果表明两者的相对误差小于5%,从而验证了回转精度矩阵闭环解析模型的正确性。分析了柔性铰链的材料参数(弹性模量E、泊松比ν)以及结构参数(铰链高度h、铰链厚度t、铰链长度l和圆角半径r)对回转精度的影响,结果表明:
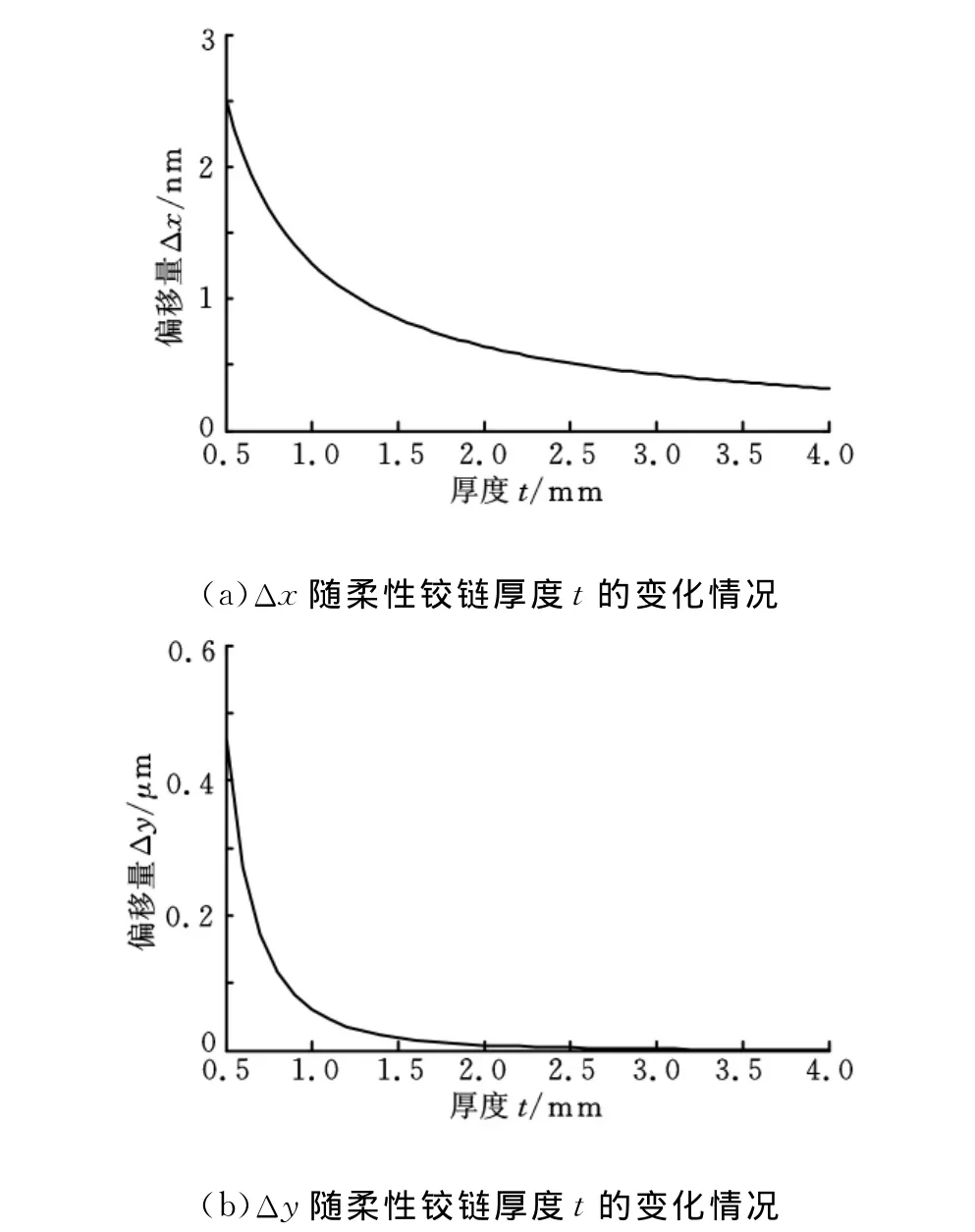
图6 回转精度随柔性铰链厚度t的变化图
(1)直梁圆角型柔性铰链材料的弹性模量E越大、泊松比ν越小,其回转精度越高。
(2)直梁圆角型柔性铰链的高度h越大时,其回转精度越高。
(3)当量纲一参数0≤s≤1,3≤q≤10时,随着s的增大、q的减小,回转精度越来越高。因此当柔性铰链的厚度t一定时,圆角半径r越大,铰链长度l越小,其回转精度就越高。
(4)当柔性铰链的结构参数h、r、l一定,且0.5mm≤t≤4mm时,随着t的增大,回转精度非线性增高,变化速率越来越小。
本文建立的直梁圆角型柔性铰链回转精度矩阵闭环解析模型,可为柔性铰链以及柔顺机构的设计优化提供理论依据。
[1]Shibazaki Y,Shi K.Apparatus for Holding Optical Element,Barrel,Exposure Apparatus and Device Producing:US,0183064[P].2007-08-09.
[2]Rau J,Schoeppach A,Weber U.Objective with at Least One Optical Element:US,7239462[P].2007-07-03.
[3]Michael T R H,Hilgers R,Merz E,et al.Optical Imaging Device,Particularly an Objective,with at Least One Optical Element:US,6191898[P].2001-02-20.
[4]张景和,廖江红,刘伟,等.二元光学元件激光直接写入设备的研制[J].仪器仪表学报,2001,22(2):154-157.
Zhang Jinghe,Liao Jianghong,Liu Wei,et al.Manufacture of Laser Direct Lithography Equipment of Binary Optics Elements[J].Chinese Journal of Scientific Instrument,2001,22(2):154-157.
[5]Ryu J W,Gweon D,Moon K S.Optimal Design of a Flexure Hinge BasedXYθZWafer Stage[J].Precision Engineering,1997,21:18-28.
[6]Kuan Y Y,Lu Tienfu.Kinetostatic Modeling of 3-RRR Compliant Micro-motion Stages with Flexure Hinges[J].Mechanism and Machine Theory,2009,44:1156-1175.
[7]吴鹰飞,李勇,周兆英,等.蠕动式X-Y-θ微动工作台的设计实现[J].中国机械工程,2001,12(3):263-266.
Wu Yingfei,Li Yong,Zhou Zhaoying,et al.Design and Develepment of an Inchworm Type ofX-Y-θMicro Stage[J].China Mechanical Engineering,2001,12(3):263-266.
[8]王林,李达成,曹芒.X射线干涉仪中单晶硅微动工作台的研制[J].仪器仪表学报,2000,21(6):654-656.
Wang Lin,Li Dacheng,Cao Mang.High-accuracy Silicon Translation Stage for X-ray Interferometry[J].Chinese Journal of Scientific Instrument,2000,21(6):654-656.
[9]Smith S T,Chetwynd D G,Bowen D K.Design and Assessment of Monolithic High Precision Translation Mechanisms[J].J.Phys.E:Sci.Instrum.,1987,20:977-983.
[10]Kim H S,Kim E J,Song B S.Diamond Turning of Large Off-axis Aspheric Mirrors Using a Fast Tool Servo with On-machine Measurement[J].Journal of Materials Processing Technology,2004,146:349-355.
[11]吴丹,谢晓丹,王先逵.快速刀具伺服机构研究进展[J].中国机械工程,2008,19(11):1379-1385.
Wu Dan,Xie Xiaodan,Wang Xiankui.Research Review of Fast Tool Servo[J].China Mechanical Engineering,2008,19(11):1379-1385.
[12]戴一帆,杨海宽,王贵林,等.压电陶瓷驱动的超精密快刀伺服系统的设计与研制[J].中国机械工程,2009,20(22):2717-2721.
Dai Yifan,Yang Haikuan,Wang Guilin,et al.Design and Development of an Ultra-precision Fast Tool Servo System Driven by Piezoelectric Ceramic[J].China Mechanical Engineering,2009,20(22):2717-2721.
[13]Lobontiu N,Paine J S N,Garcia E,et al.Design of Symmetric Conic-section Flexure Hinges Based on Closed-form Compliance Equations[J].Mechanism and Machine Theory,2002,37(5):477-498.
[14]Lobontiu N,Paine J S N.Corner-filleted Flexure Hinges[J].ASME Mech.Design,2001,123(3):346-352.
[15]张志杰,袁怡宝,朴伟英.典型柔性铰链回转精度性能计算与分析[J].纳米技术与精密工程,2007,5(3):200-204.
Zhang Zhijie,Yuan Yibao,Piao Weiying.Rotation Precision Calculation and Analysis of Typical Flexure Hinges[J].Nanotechnology and Precision Engineering,2007,5(3):200-204.
[16]Xu W,King T G.Flexure Hinges for Piezo-actuator Displacement Amplifiers:Flexibility,Accuracy and Stress Considerations[J].Precision Engineering,1996,19(1):4-10.
[17]Ryu J W,Gweon D G.Error Analysis of a Flexure Hinge Mechanism Induced by Machining Imperfection[J].Precision Eng.,1999,21(2):83-89.

