基于分段遗传算法的桁架拓扑优化设计
王 琦 饶碧波 王源博 李 应
南昌航空大学,南昌,330063
0 引言
桁架(多杆)结构被广泛用于飞机、汽车等结构设计中。特别是在飞机结构设计中,除满足强度、刚度和可靠性要求外,还力求结构质量最小[1]。拓扑优化是结构设计的一种常用方法。对于1975年美国密西根大学Holland教授提出的遗传算法(genetic algorithm,GA)[2],多数研究者将工作重点置于改进简单遗传算法或将其与其他算法混合后运用到实际工程优化问题中去。如,浙江工业大学的范佳静等[3]将改进遗传算法用于制造单元模型的优化求解;合肥工业大学的许闻清等[4]运用改进的遗传模拟退火算法求解动力总成悬置系统的优化设计;许素强等[5]在国内首次运用遗传算法解决桁架结构的拓扑优化;唐文艳等[6]和黄冀卓等[7]分别在ε-松弛技术和结构有限元分析的基础上,引入新型拓扑变量,改造拓扑模型,运用改进遗传算法进行桁架拓扑优化,大大提高了优化精度。张喜清等[8]采用有限元分析方法对变速箱箱体减重问题进行了拓扑优化;赵龙彪等[9]将基于比例微分控制思想的优化准则运用到拓扑优化中,取得了良好的效果。简单遗传算法的工程应用目前存在的问题是:早熟或难以收敛,难以求解复杂的约束优化问题[2,10-11]等。具体到结构优化方面,还存在以下问题:当处理约束问题时,优化效果常受制于优化模型及罚函数参数(罚参数)的设计[5,7,10-11];另外,设计变量和结构分析次数增多,将降低遗传算法的收敛速度,且其时间复杂度也是一个有待解决的问题。为提高遗传算法的应用效率,本文将简单遗传算法加以若干改进,提出分段遗传算法,并通过桁架结构拓扑优化的算例,验证了改进算法的可行性和有效性。
1 分段遗传算法步骤与简析
1.1 分段遗传算法步骤
分段遗传算法将遗传算法的运行过程分为“粗搜”和“精搜”两个阶段,其程序流程如图1所示。
图1中,把初始种群中适应度最高的一个个体作为最优个体进行保留,对剩余的2K个个体进行遗传操作[2],产生新一代种群。
1.1.1 个体适应度最佳保留原则
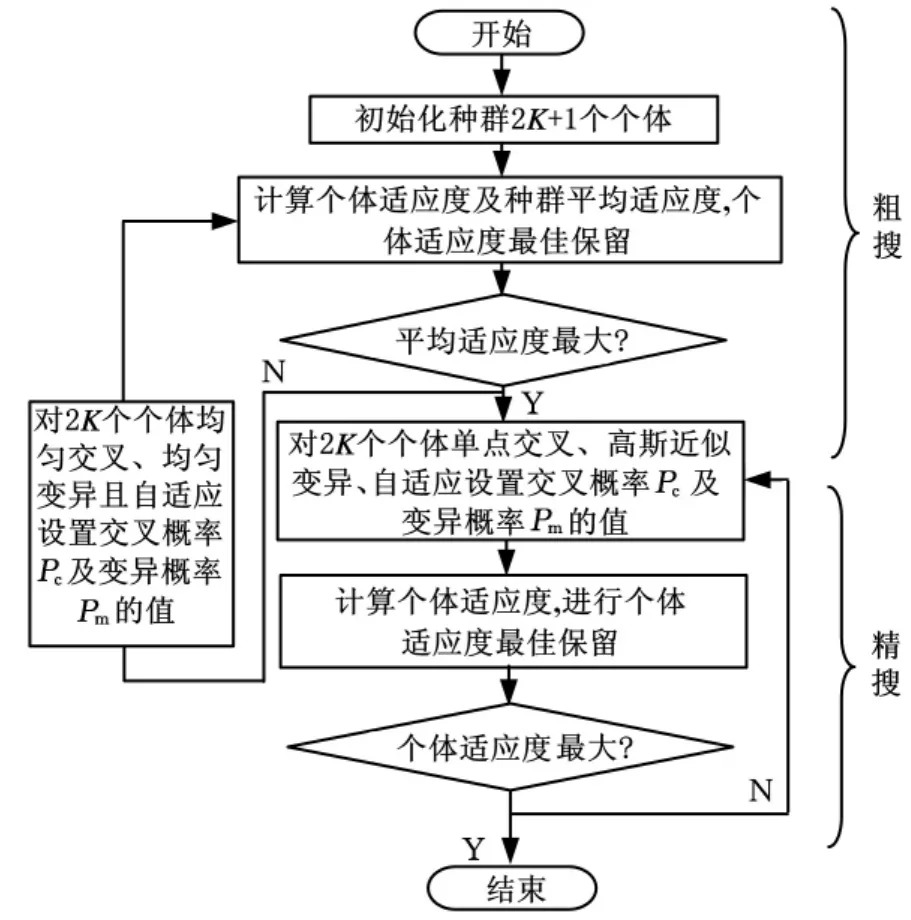
图1 分段遗传算法程序流程
(1)若新一代种群中的最优个体优于上一代种群中的最优个体,但上一代种群中的最优个体又优于新种群中适应度最差的个体,则保留新一代种群中的最优个体,并用上一代种群中的最优个体替换新种群中适应度最差的个体,连同其他新个体参与下一轮遗传操作。反之,若上一代种群的最优个体不优于新种群中适应度最差的个体,则不作替换,保留新一代最优个体,剩余新个体参与下一轮遗传操作。
(2)若新一代种群中的最优个体不优于上一代种群中的最优个体,则上一代种群中的最优个体仍然保留,全部新个体参与下一轮遗传操作。
1.1.2 “粗搜”阶段
(1)均匀交叉:两个配对个体每个基因座上的基因都以相同的交叉概率进行交换。
(2)均匀变异:以某一较小变异概率改变个体每个基因座上的原有基因值。上述Pc和Pm的取值与个体适应度的关系分别如图2和图3所示。
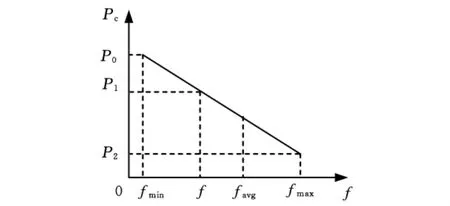
图2 自适应交叉概率
在图2和图3中,fmin为某一代种群中个体的最小适应度值;favg为某一代种群的平均适应度值;f为某一代种群中某个个体的适应度值;fmax为某一代种群中个体的最大适应度值。
计算交叉概率Pc及变异概率Pm的表达式为
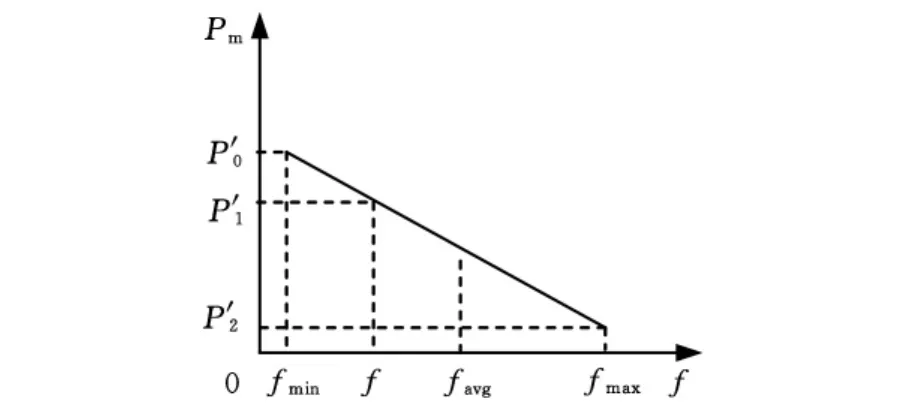
图3 自适应变异概率
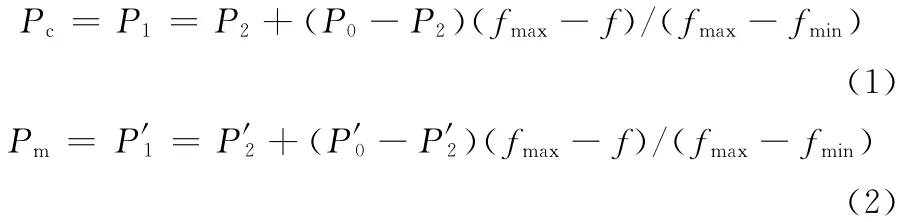
其中,P0、P2、P′0、P′2之取值,视适应度函数及其尺度变换的具体情况而定,但在多数情况下,它们的经验参考值分别是:P0=0.9,P2=0.6,P′0=0.1,P′2=0.001[8]。
当新种群的平均适应度等于上一代种群的平均适应度时,则新一代种群进入“精搜”阶段。
1.1.3 “精搜”阶段
(1)单点交叉:交换交叉点右边的部分基因。
(2)高斯近似变异:用正态分布的一个随机数来替换原有的基因值。
1.2 分段遗传算法简析
在算法运行的前期,均匀交叉和均匀变异易于使个体位置靠前的部分基因得到调整,搜索范围迅速扩大,故可称为“粗搜”;在后期,单点交叉和高斯近似变异又易于保护个体位置靠前的部分基因不受破坏,使得搜索能控制在一定范围内,故称为“精搜”。一般连续函数极值点附近点的函数值普遍大(小)于定义域内其他点的函数值。由此可知:如果算法在“粗搜”阶段找到一个平均适应度最高的种群点,则全局最优解就应在该种群点附近或其中。本文1.1节所设计的最优个体保留及Pc和Pm的自适应设置,不仅可使迭代中出现的最优值得以保留不致丢失,而且能在加快收敛速度的前提下,基本保证平均适应度达到最大值之前,各代种群的平均适应度逐代增大,而一旦某代种群的平均适应度等于它前一代种群的平均适应度,则表明该代种群的平均适应度已经达到最大值。以此作为“粗搜”阶段结束的判定条件。这样设立的判定条件,不仅可以避免设定阈值时的繁琐试验过程,而且对于不同的优化问题具有一定的通用性。以该平均适应度达到最大值的种群点为操作对象,进入“精搜”阶段,调整交叉、变异类的各种相关遗传操作因子,转入局部区域重点搜索,最终快速找到全局最优解。
2 算例验证
2.1 拓扑优化数学模型
一般情况下,带约束非线性规划问题的数学模型为

其中,g(x)= (g1(x),g2(x),…,gm(x)),j=1,2,…,m。对可行域S={x|gj(x)≤0}引入外点惩罚函数:
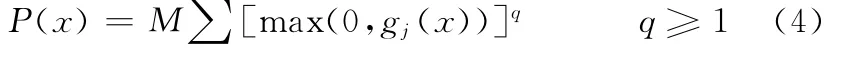
在选区内构造一个单调递增且趋于无穷的罚因子列:0<M1<M2<…<Mk<…,构成一系列无约束非线性规划问题:
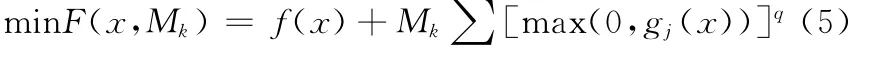
从而将原带约束非线性规划问题转化为一系列无约束非线性规划问题。
一般地,拓扑优化的数学模型(TP)为[5]:

式中,Ai、ρi、Li分别为第i杆之截面积、密度和杆长,其中,Ai为截面积设计变量;n为杆件总数;m为节点总数;p为载荷总数;ND为结构维数,即2或3;σi为第i杆之许用应力值为第j节点在i方向的允许位移值。
在上述模型中,式(7)和式(8)为约束条件。对拓扑优化而言,一般允许截面积为零,此时,相应地取消应力约束。同理,当连接某节点的各杆截面积均为零时,该节点的位移约束也应取消。
2.2 无约束化处理
力与位移约束,其分段形式为
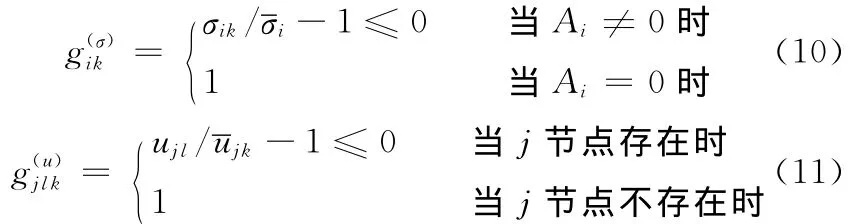
综上,可用外点罚函数法将原问题(TP)转化为遗传算法(GA)所要求的形式,即

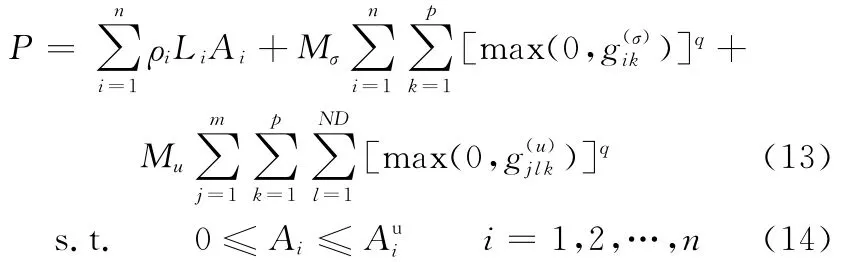
式中,Mσ、Mu分别为应力约束罚参数和位移约束罚参数。
2.3 算例
选用3个桁架结构拓扑优化作为算例,对上述拓扑模型,分别用简单遗传算法与分段遗传算法进行求解。
2.3.1 九杆结构
九杆结构如图4所示,有5个节点,9根杆件,同时有应力、位移两种约束。各杆参数值为:弹性模量E=29GPa,密度ρ=0.83g/mm3,许用应力取值分别是:-18MPa≤≤20MPa(i=1,2,9),-12MPa ≤≤ 20MPa(其 余),uji=±1.5mm(i=2,4,5;j=1,2)。在节点4处,有一载荷Px,取值为100N,在节点2处,有一载荷Py,取值为-100N;变量链化关系为:A1=A2,A3=A4,A5=A6,A7=A8。
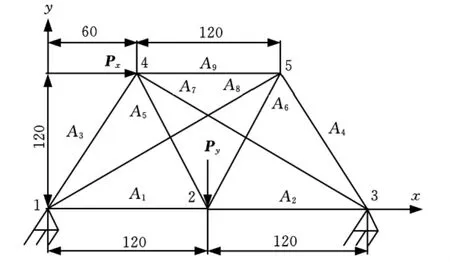
图4 九杆结构
在应用简单遗传算法进行优化时,各参数设置为:Mσ=2000,Mu=1,种群尺度SP=50,Pc=0.9,Pm=0.005,终止代数T=100。使用分段遗传算法进行优化时,除保留Mσ=2000、Mu=1、T=100外,其余参数设置调整为:SP=51,Pc及Pm按式(1)和式(2)进行自适应设置。运用2种算法对九杆结构进行优化,优化拓扑如图5所示,所得数据见表1,其进化曲线如图6所示。
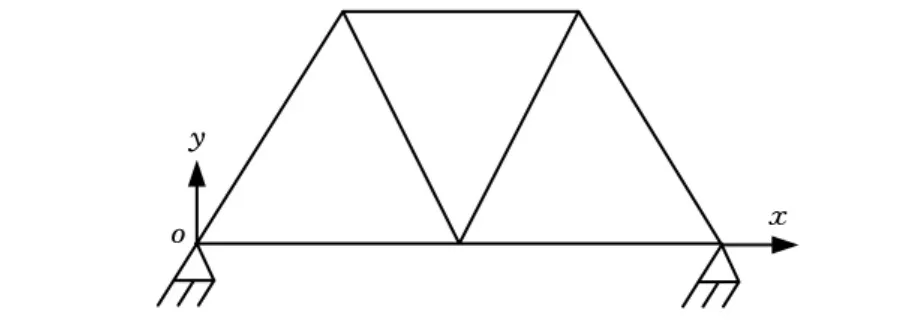
图5 九杆结构优化拓扑
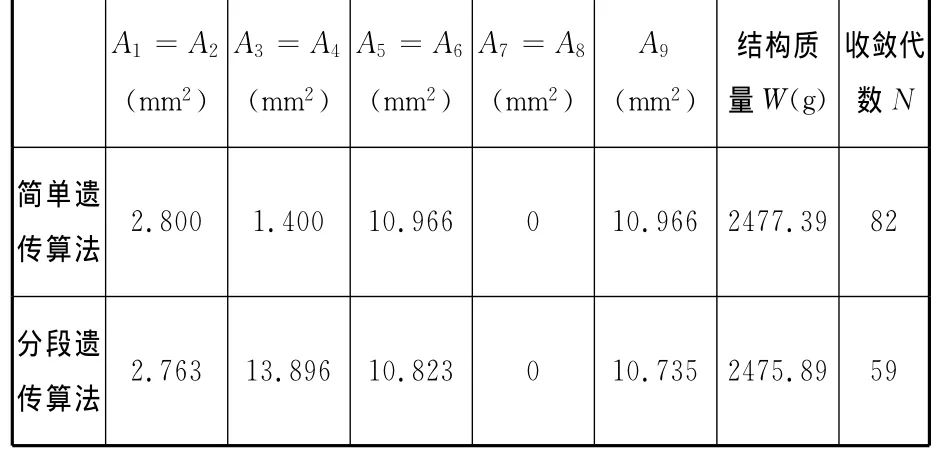
表1 九杆结构优化数据
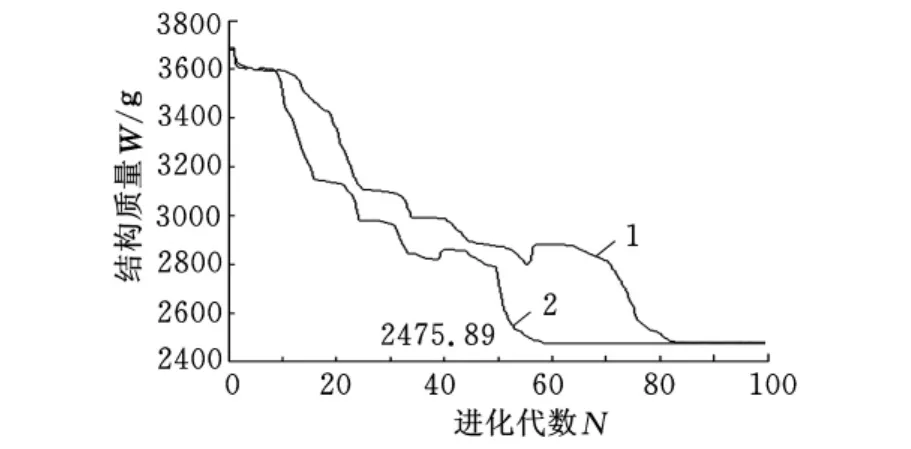
图6 九杆结构进化图
2.3.2 十杆结构
图7所示为十杆结构,该结构有6个节点、10根杆件,即有10个独立的设计变量。对于全部杆件有:E=10TPa,ρ=0.1g/mm3=±25GPa。在节点2和节点4上各有一个向下的载荷P,取值为100N;节点1、2、3、4的ui=±2mm(i=1,2,3,4)。
运用简单遗传算法优化时的控制参数为:Mσ=1000,Mu=1,SP=50,Pc=1.0,Pm=0.01,T=100。使用分段遗传算法进行优化时,除保留Mσ=1000、Mu=1、T=100外,其余参数设置与2.3.1节相同。运用2种算法对十杆基础结构进行优化,优化拓扑如图8所示,所得数据见表2,进化曲线如图9所示。
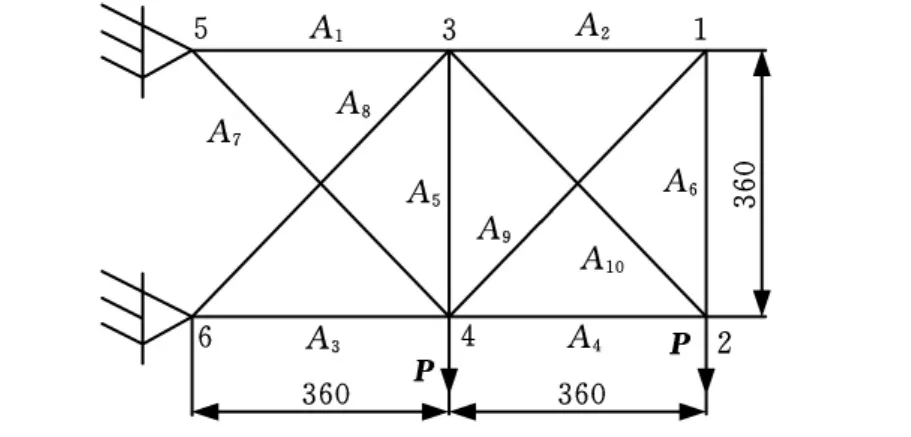
图7 十杆结构
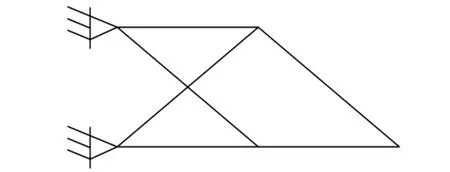
图8 十杆结构优化拓扑
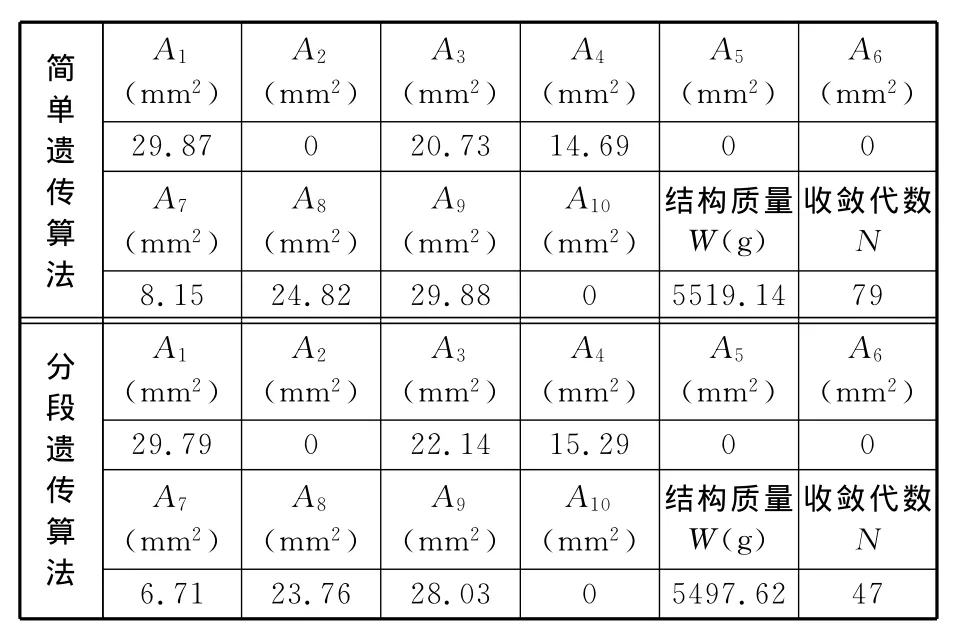
表2 十杆结构优化数据
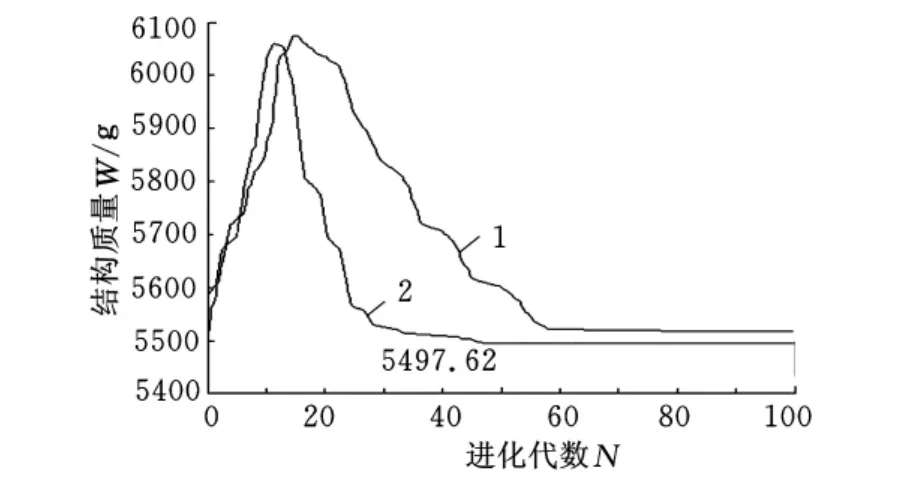
图9 十杆结构进化图
2.3.3 七十二杆结构
七十二杆空间桁架为一塔架结构,共有72根杆件,20个节点,如图10所示。对于全部杆件有:E=10TPa,ρ=0.1g/mm3,σi=±25GPa。位移约束为塔顶4个节点在空间三坐标方向的位移值不得超过±0.25mm,各杆件的截面积最小值为0.1mm2。
由于结构对称,可将整个结构分为4层,每层可分为4组,共16组,因此,72根杆件可设置为16个设计变量。顶层杆件的分组情况见表3。该结构受到2个工况载荷,见表4。
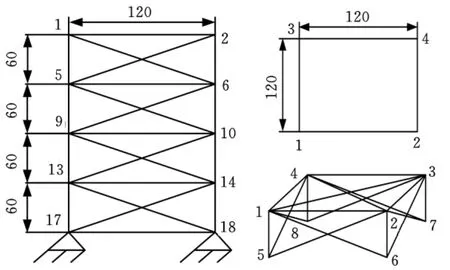
图10 七十二杆结构

表3 七十二杆结构顶层杆分组情况
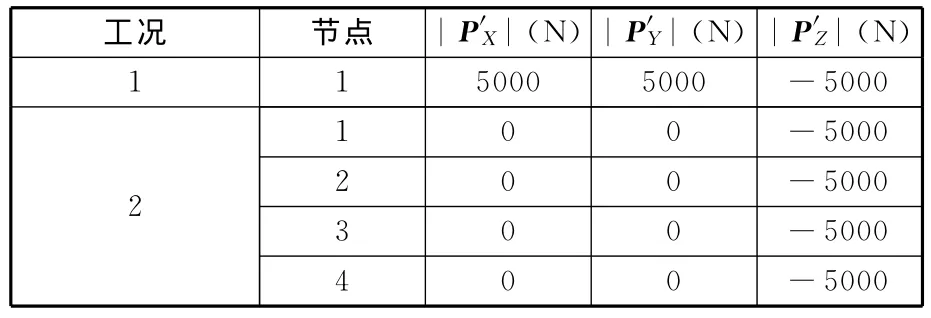
表4 七十二杆结构工况荷载情况
运用简单遗传算法优化时的控制参数为:Mσ=1000,Mu=1,SP=50,Pc=1.0,Pm=0.01,T=200。在使用分段遗传算法进行优化时,除保留Mσ=1000、Mu=1、T=200外,其余参数设置与2.3.1节相同。运用2种算法对七十二杆结构进行优化,结构优化拓扑如图11所示。所得数据见表5和表6。进化曲线如图12所示。
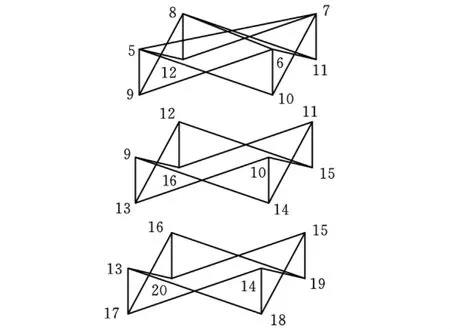
图11 七十二杆结构优化拓扑
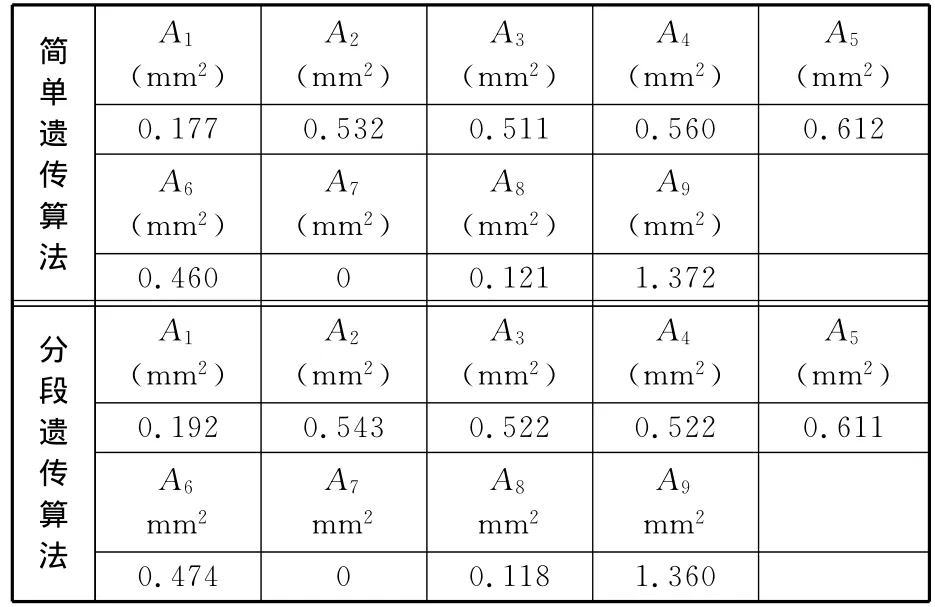
表5 七十二杆结构优化数据(1)
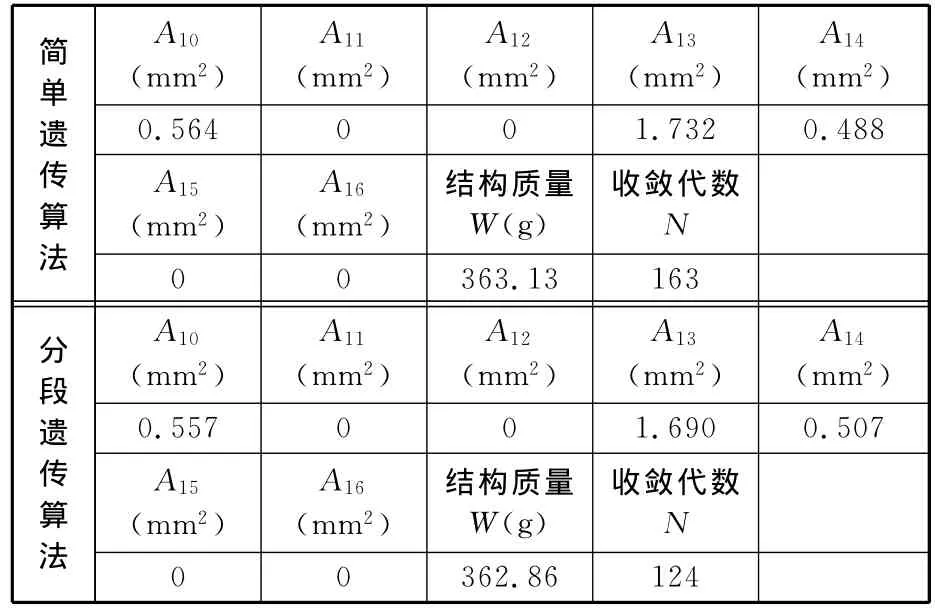
表6 七十二杆结构优化数据(2)
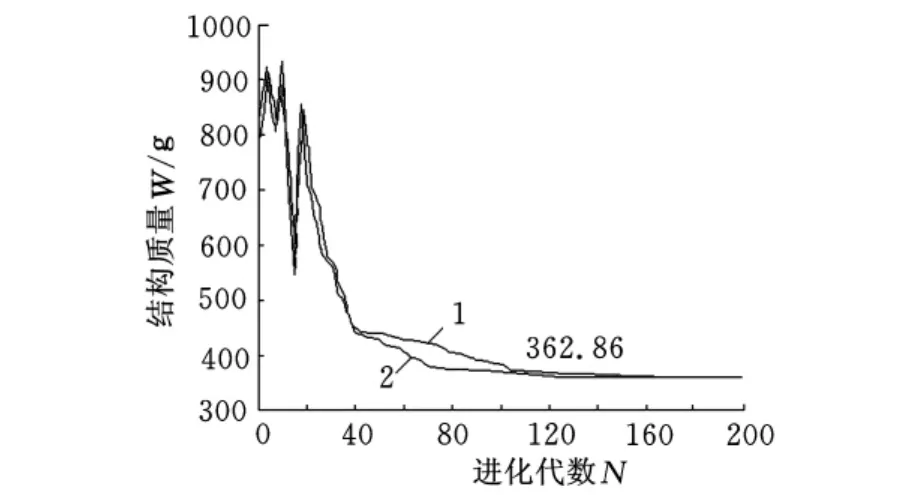
图12 七十二杆结构进化曲线
3 结束语
虽然本文的分段遗传算法操作步骤及程序编制稍显繁复,不及直接使用简单遗传算法工具箱快捷,但相比其他改进遗传算法更简单,且具一定的通用性。3个桁架结构拓扑优化的算例表明:当优化较为复杂的桁架结构时,无论是收敛速度还是收敛精度,分段遗传算法都优于简单遗传算法,说明本文分段遗传算法的方案是可行、有效的。
[1]王志瑾,姚卫星.飞机结构设计[M].北京:国防工业出版社,2007.
[2]雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[3]范佳静,冯定忠.基于改进遗传算法的制造单元设计研究[J].中国机械工程,2011,22(1):39-44.
Fan Jiajing,Feng Dingzhong.Study on Manufacturing Cellular Design Based on Advanced Genetic Algorthm[J].China Mechanical Engineering,2011,22(1):39-44.
[4]许闻清,陈剑.基于改进遗传模拟退火算法的动力总成悬置系统优化设计[J].中国机械工程,2011,22(1):878-881.
Xu Wenqing,Chen Jian.Optimization Design of Powertrain Mounting System Based on Improved Genetic Simulated Annealing Algorithm[J].China Mechanical Engineering,2011,22(1):878-881.
[5]许素强,夏人伟.桁架结构拓扑优化与遗传算法[J].计算结构力学及其应用,1994,11(4):436-445.
Xu Suqiang,Xia Renwei.Topological Optimization of Truss Structure via the Genetic Algorithm[J].Computational Structural Mechanics and Applications,1994,11(4):436-445.
[6]唐文艳,顾元宪,郭旭.求解具有奇异性的桁架拓扑优化的遗传算法[J].计算力学学报,2004,21(2):191-195.
Tang Wenyan,Gu Yuanxian,Guo Xu.Genetic Algorithm Applied in Solving Topology Optimization of Truss Structures with Singular Optima[J].Chinese Journal of Computational Mechanics,2004,21(2):191-195.
[7]黄冀卓,王湛.基于遗传算法的离散型结构拓扑优化设计[J].工程力学,2008,25(5):32-38.
Huang Jizhuo,Wang Zhan.Topology Optimization Design for Discrete Structures Using Genetic Algorithm[J].Engineering Mechanics,2008,25(5):32-38.
[8]张喜清,项昌乐,刘辉.多工况下变速箱箱体结构的拓扑优化设计[J].中国机械工程,2011,22(15):1779-1883.
Zhang Xiqing,Xiang Changle,Liu Hui.Topology Optimization Design of Gearbox Housing under Multiple Loading Cases[J].China Mechanical Engineering,2011,22(15):1779-1883.
[9]赵龙彪,高亮,陈志敏,等.基于比例微分优化准则的拓扑优化方法[J].中国机械工程,2011,22(3):345-350.
Zhao Longbiao,Gao Liang,Chen Zhimin,et al.A Proportional and Differential Optimality Criterion Method for Topology Optimization[J].China Mechanical Engineering,2011,22(3):345-350.
[10]王小平,曹立明.遗传算法——理论、应用与软件现实[M].西安:西安交通大学出版社,2002.
[11]Bendsoe M P,Sigmund O.Topology Optimization:Theory,Method and Applications[M].New York:Springer,2003.

