LMD的LabVIEW实现及在滚动轴承故障诊断中的应用
唐贵基,王晓龙
(华北电力大学 机械工程学院,河北 保定 071003)
2005年Smith Jonathan S在EMD理论基础上提出一种新的时频分析方法——局部均值分解法(Load Mean Decomposition,LMD),该方法同样具有自适应性,可以将任何一个复杂的多分量复合信号分解成多个乘积函数(Product Function,PF)分量及一个余量相加的形式,PF分量能够真实地反映原信号的信息[1]。相对于EMD来说,LMD受端点效应影响较小,并且可以避免EMD 算法自身存在的问题,用于故障诊断,具有一定的优势。鉴于LMD在故障诊断领域良好的应用前景以及LabVIEW软件在信号分析处理方面的广泛应用,根据LMD算法理论开发出LabVIEW的LMD模块,将更有利于测试系统的搭建。
1 LMD算法简介
对于给定的信号x(t),LMD算法流程为[2]:
(1)确定原信号x(t)的所有局部极值点ni。
(2)计算相邻极点的均值和包络估计值
(1)
(2)
(3)均值和估计值分别用直线连接后进行滑动平均处理,得到局部均值函数m11(t)和包络估计函数a11(t)。
(4)获得包络信号a1(t)和纯调频信号s1n(t)。
h11(t)=x(t)-m11(t),
(3)
s11(t)=h11(t)/a11(t),
(4)
如果s11(t)的包络估计函数a12(t)≠1,则将其作为原始数据重复上述过程,直到其包络估计函数a1(n+1)(t)=1,则得到纯调频信号s1n(t),则包络信号为
(5)
包络信号a1(t)即为瞬时幅值,通过纯调频信号s1n(t)即可求得瞬时频率f1(t)为
(6)

(5)求得乘积函数分量。将包络信号a1(t)和纯调频信号相乘即可得到第1个乘积函数分量,即
PF1(t)=a1(t)s1n(t)。
(7)
原信号x(t)减去PF1(t)后获得新信号u1(t),将u1(t)作为原始数据重复上述过程k次,直到余量uk(t)为单调函数或常数。
2 LMD算法的LabVIEW程序实现
LMD算法通过图形化编程语言LabVIEW实现,经过模块化划分后的主程序框图如图1所示。
LMD主程序中包含极值延拓、样条插值、分量判别、分量求取、余量判别、瞬时频率求取、形态学滤波共7个子VI。其中极值延拓、分量求取和瞬时频率求取这3个子模块较为重要。
2.1 极值延拓子模块
同EMD算法相比,LMD算法的端点效应程度较轻,但为了使分解过程更准确,仍需对端点进行处理。如图2所示,该模块采用包络极值延拓法[3]来减少分解过程中端点效应的影响。
2.2 样条插值子模块
由于利用滑动平均法来平滑均值和包络函数会产生相位差,而且平滑步长的选择主观性过大,分解过程存在较大误差[4]。如图3所示,为了减小误差,该模块采用三次样条插值方法代替滑动平均法,局部均值函数可由上、下包络线相加后求平均值得到,包络估计函数可由上、下包络线相减取绝对值后求平均值得到[5]。
2.3 分量判别子模块
分量判别子模块通过判断当前信号是否满足PF分量判别依据来控制循环过程,如果满足条件,则直接输出PF分量序列;如果未满足条件,则持续循环,直到获得一个PF分量。
2.4 分量求取子模块
分量求取子模块可通过当前获得的包络估计函数序列和纯调频信号序列直接计算出PF分量和瞬时幅值序列。
2.5 余量判别子模块
为了避免分解过程进入死循环,通过余量判别子模块对残余分量进行控制,判断当前信号是否分解结束,是否需要进一步继续分解。
2.6 瞬时频率求取子模块
由于瞬时频率在极值点附近存在畸变的情况,因此采用“直接法”[6]来求取PF分量的瞬时频率,该方法简单有效,并且不会出现没有物理意义的负频率,计算获得的瞬时频率均为正值,程序框图如图4所示。

图4 瞬时频率求取子模块程序框图
2.7 形态学滤波子模块
LMD模块对仿真信号分解后获得的瞬时幅值和瞬时频率曲线存在少许毛刺,形态学滤波子模块利用形态学滤波算法[7]对其进行平滑处理。
3 轴承故障诊断实例检验
采用QPZZ故障诊断试验台模拟N205圆柱滚子轴承故障,并利用开发的LMD模块对测得的振动数据进行分析处理,以此来验证该模块的可靠性及有效性。采用压电加速度传感器对振动信号进行数据采集,采样频率设置为12 800 Hz。1 440 r/min转速时,N205轴承故障的特征频率见表1。

表1 N205滚动轴承故障的特征频率 Hz
3.1 滚子故障诊断
滚子发生故障时,由于滚子在自转的同时也随保持架一起旋转,因此损伤点所处位置及受载呈周期性变化,系统固有频率信号、保持架转频信号、滚子故障特征频率信号互相调制生成滚动体故障信号[1],故障信号的时域波形及频谱如图5所示。
从图5可以看出,时域波形上出现明显规律性冲击,频谱中出现边频调制的现象,由此说明轴承出现局部损伤。对故障信号进行LMD分解后得到6个PF分量,省略掉余量后各分量波形如图6所示。
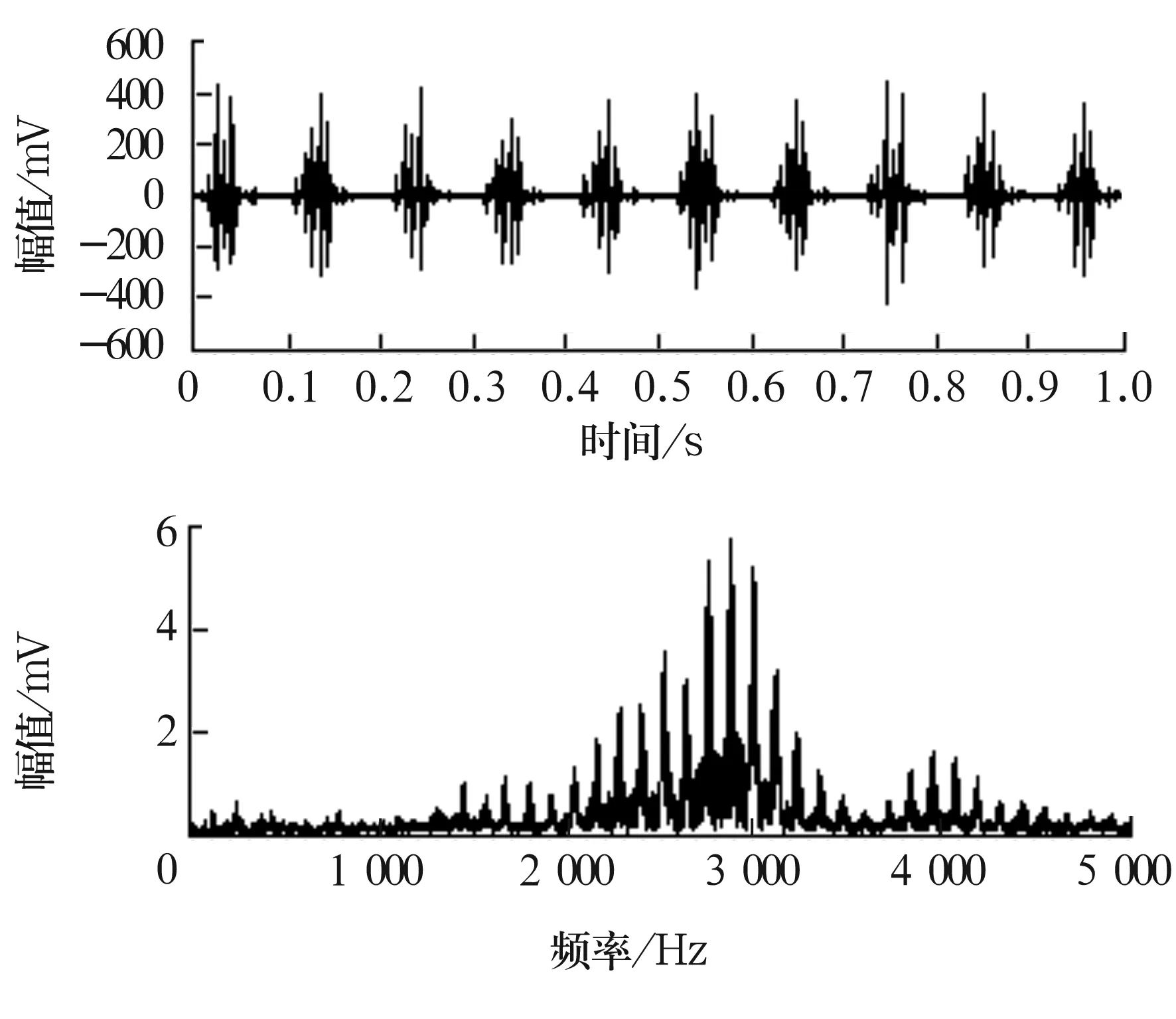
图5 滚子故障信号的时域波形及频谱
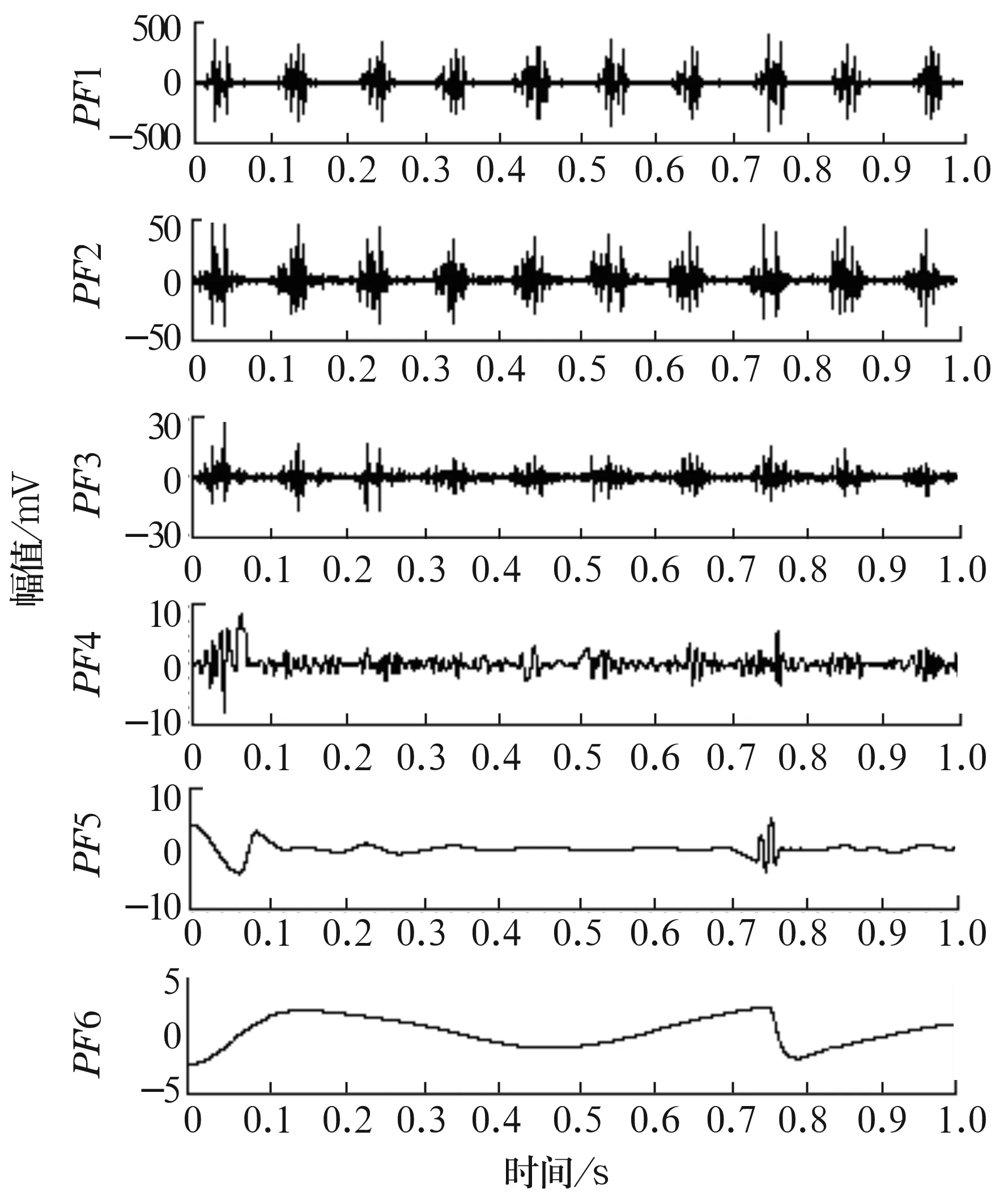
图6 滚子故障信号LMD分解结果
选取经过LMD分解获得的PF1分量的瞬时幅值曲线做进一步频谱分析,得到的频谱如图7所示。从图中发现,频谱中有6处相对明显的谱线,并出现调制现象,间隔频率为保持架的旋转频率。104,113和133 Hz为保持架转频调制边频带;10和20 Hz分别为保持架的转频及2倍频;123 Hz为滚子故障特征频率。结果与理论计算相吻合,由此可以说明,滚子存在局部缺陷。

图7 滚动体故障信号PF1分量的瞬时幅值曲线的频谱
3.2 内圈故障诊断
内圈发生故障时,由于内圈随转轴一起旋转,因此内圈上的故障点与滚子的接触位置及承受的载荷也呈周期性变化,系统固有频率信号、轴转频信号、内圈故障特征频率信号相互调制生成内圈故障信号[8],故障信号的时域波形及频谱如图8所示。
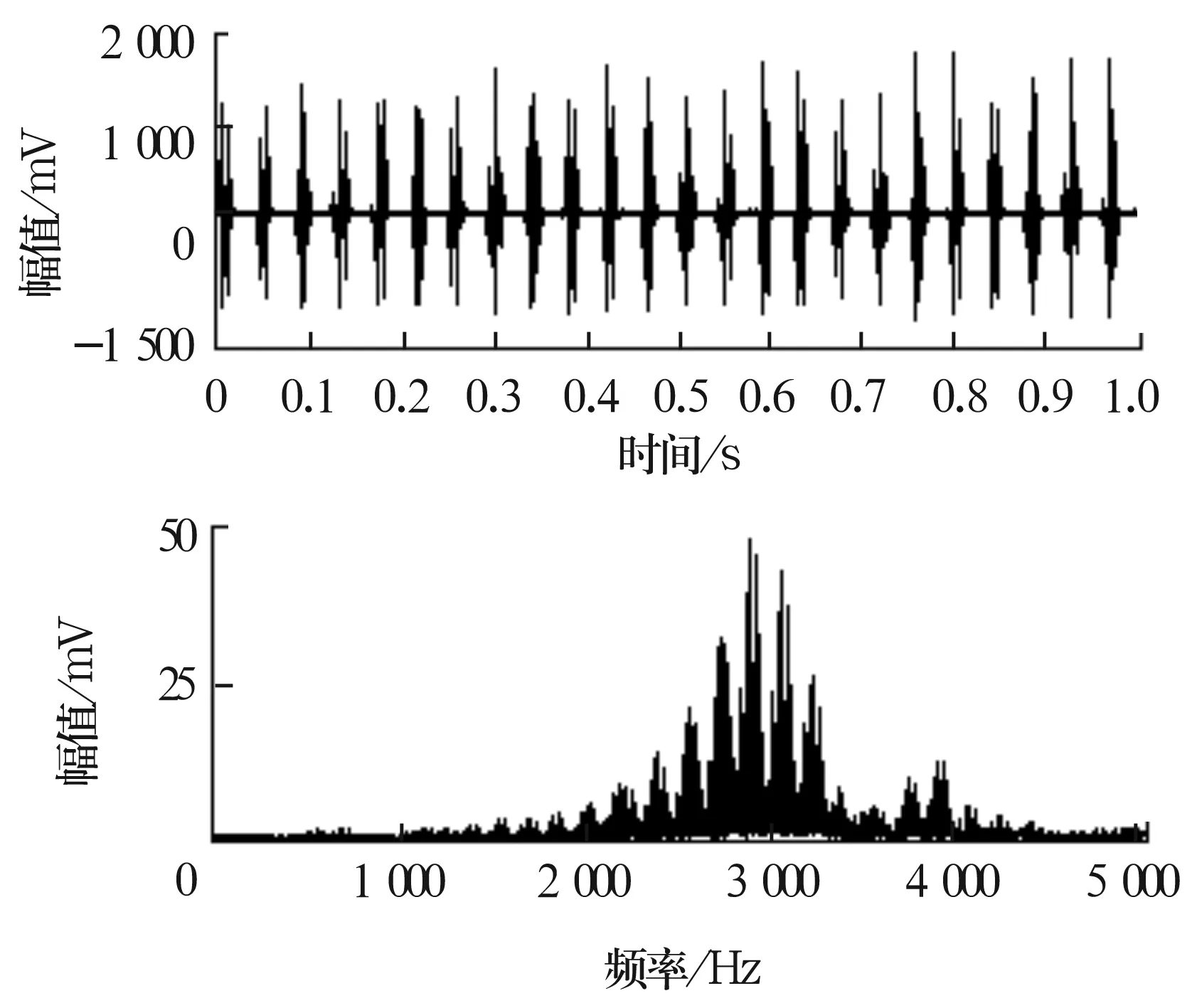
图8 内圈故障信号的时域波形及频谱
从图8可以看出,由于内圈存在局部缺陷并且接触位置及受载大小的不断变化,时域波形和频谱上同样出现规律性冲击和边频调制的现象。在此省略内圈故障信号的LMD分解结果,只选取分解后得到的PF1分量的瞬时幅值曲线作频谱分析,结果如图9所示。

图9 内圈故障信号PF1分量的瞬时幅值曲线的频谱
从图中发现,频谱有6处峰值比较明显,同样出现调制现象,间隔频率为轴的转频,124,148和196 Hz为轴转频调制边频带;24和48 Hz分别为轴的转频及2倍频;172 Hz为内圈故障特征频率。由此可以断定,内圈存在局部缺陷。
3.3 外圈故障诊断
外圈发生故障时,由于外圈固定,因此故障所处的位置及受载的大小保持不变,故障信号是以系统固有频率为高频载波,外圈特征频率为调制频率的调制信号[7],信号的时域波形及频谱如图10所示。

图10 外圈故障信号的时域波形及频谱
与前两种故障不同,由于外圈损伤点所处位置及受载大小基本不变,因此时域波形上的振动冲击的振幅比较均匀,外圈故障信号LMD分解获得的PF1分量的瞬时幅值曲线的频谱如图11所示。

图11 外圈故障信号PF1分量的瞬时幅值曲线的频谱
从图中发现,频谱在116和233 Hz处存在明显的峰值,分别对应着轴承外圈故障特征频率及2倍频,分析结果与理论计算相符,因此判定,外圈存在局部故障。
4 结束语
同EMD算法一样,LMD算法也是一种适合处理非线性非平稳信号的时频分析方法,该方法可以有效地应用于齿轮、轴承或转子系统的故障诊断。在LabVIEW平台上将LMD算法程序化,并通过对实测轴承故障信号的分析,证明基于LabVIEW平台开发的LMD模块能够准确地对故障信号进行分析,顺利提取出轴承的故障特征频率信息。

