形态变换与峭度在轴承故障诊断中的应用

滕明春，石林锁，王新军，李建毅

(第二炮兵工程大学 五系，西安 710025)

在轴承的故障诊断中，消噪是信号处理的基础。较为经典的方法是采用数字或模拟滤波器，常见的小波分析及EMD在消噪中取得了一定的进展。但是小波去噪中，小波基、分解层数以及阈值的确定是一个难题[1];EMD得到的模态分量含有干扰成分，影响故障的准确判断[2]。形态滤波属于非线性滤波，在对信号进行滤波时，针对的是信号的几何结构特征而与信号的频率无关，因此在图像处理中的形状识别、边缘检测等方面得到了广泛的应用。近年来，不少学者将形态滤波应用到轴承故障信号滤波中[3-4]。

对轴承故障的特征提取，目前较为通用的方法是包络分析[5]。但是该方法需要依靠经验确定解调参数，实际应用比较麻烦。因此，结合形态滤波、小波包分解、峭度和形态梯度变换，提出先将信号经过广义形态滤波组滤波；再进行小波包分解，并计算每个频段的峭度值；而后选取最大峭度值所在频段进行形态梯度变换以提取冲击成分；最后根据冲击成分的频域特点实现轴承故障状态的诊断。

1 遗传算法优化的广义组合滤波器组

在形态滤波器中，组合形态滤波器比开闭、闭开滤波器具有更小的均方根和统计偏移，而广义组合滤波器又能够克服组合滤波器在构建中采用相同尺度结构元素带来偏移的不足，因此应用最为广泛。广义组合滤波器的定义为

(1)

式中：GCO,GOC为广义闭开、开闭滤波器。

对于形态滤波器，结构元素的选择是关键，常用的结构元素有直线形、三角形、圆形、正弦形和钻石形等。对于振动信号的滤波，采用三角形、圆形和直线形3种形状的结构元素可以取得较好的效果[6]。应用的经验表明，圆形结构元素对白噪声去噪效果较好，三角形结构元素对脉冲噪声去噪效果较好[7]。在实测信号的去噪处理中，由于与结构元素相似的细节能够更好地得到保存，因此所选结构元素应尽可能与待分析信号的特征接近。但在进行故障诊断时，故障信号中冲击成分的形态特征往往是难以预知的，此时很难确定采用哪一种结构元素较好。同时噪声的种类往往不止一种，采用单一的结构元素，难以取得较为满意的效果。此外，结构元素的长度和高度也将影响滤波的效果。结构元素的高度通常比信号小一个数量级[8]，而长度对滤波的效果影响更大，其选取取决于波形的宽度和采样的频率。文献[9]认为应该取为振动信号基频周期内采样点数的1/12；文献[10-11]认为采用长度为故障周期长度0.6～0.8倍的扁平形结构元素最为有效。但是在实际中，冲击的长度往往也难以预知。因此，有必要寻找一种根据信号自适应选取结构元素及其长度的方法。

综上所述，利用遗传算法对结构元素和长度进行优化，进而确定最优模型，以期达到令人满意的去噪效果。采用一维振动信号中常用的三角形、圆形和直线形3种结构元素组成滤波器组，对3种结构元素所占权重和长度进行编码。考虑到在对滤波效果进行评价时，常采用信噪比和均方根误差作为评价指标，而信噪比又由信号和噪声的能量之比取对数得到，且能量之比不变号，因此采用信号和噪声的能量比与均方根误差之商作为适应度函数。其既满足了适应度函数定号的要求，又符合信噪比大、均值误差小的信号降噪要求。初始种群的生成由两部分组成，权重和长度分别随机生成。在计算适应度值时，为保证消噪后的信号不与原始信号产生偏倚，对权重进行归一化。将信号送入广义组合形态滤波器组中，对于每一个个体，首先通过单个结构元素构成的广义组合形态滤波器滤波，前一结构元素的长度由个体决定，后一个结构元素的长度按照经验[12]，取为前一长度的2倍；然后将3种结构元素滤波的结果按照权重进行加权，计算信号和噪声的能量比和均方根误差；最后将信号和噪声的能量比以均方根误差之商作为适应度值。

2 峭度

峭度作为时域分析中常用的指标，主要用来衡量振动信号的振幅偏离正态分布的程度。其定义为

(2)

式中：N为信号的长度；x(i)为离散振动信号；μx为均值；σx为标准差。文献[13]指出，当信号的峭度值K远大于3时，说明是信噪比很高的故障信号。通过比较小波包分解后不同频段的峭度值，利用峭度值最大的原则，就可以判断出共振频率所在的频段。

3 形态梯度变换

形态学膨胀和腐蚀只能分别提取信号中的正、负脉冲信息，对于实际信号中同时具有正、负冲击的提取，则需要采用膨胀腐蚀结合构建得到的形态梯度算子。形态梯度变换(MG)的定义为信号经过膨胀和腐蚀之后的数字差分。MG可以用来检测加于稳态信号之上的暂态信号。

Ggrad=(ρ⊕b)(x)-(ρΘb)(x)。

(3)

在一维信号处理中，形态梯度算子可用于检测加于稳态信号之上的暂态信息，由于同时考虑了正、负冲击，是提取冲击信息的有力工具[14]。

4 优化的形态滤波器组的仿真试验

信号x=3sin(2π30t)+5cos(2π50t)加入均值为0，标准差为δ的随机白噪声和幅值为A的正、负脉冲信号，以检验优化广义组合形态滤波器组的滤波能力。采样频率取为1 024，采样点数为1 024。滤波效果的好坏由信噪比、均方根误差和峰值误差进行判断，其定义依次为

(4)

(5)

(6)

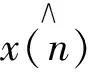
表1给出了不同参数设置下，含噪信号、广义组合滤波器滤波后信号以及遗传优化滤波得到的广义组合滤波器组滤波后的信号相对于正常信号的信噪比、均方根误差和峰值误差。很明显，遗传优化得到的滤波器组降噪后的信号，信噪比比广义组合滤波器降噪后的信号更高，均方根误差和峰值误差也要更小，证明优化的滤波器相对于广义组合滤波器具有更好的滤波效果。

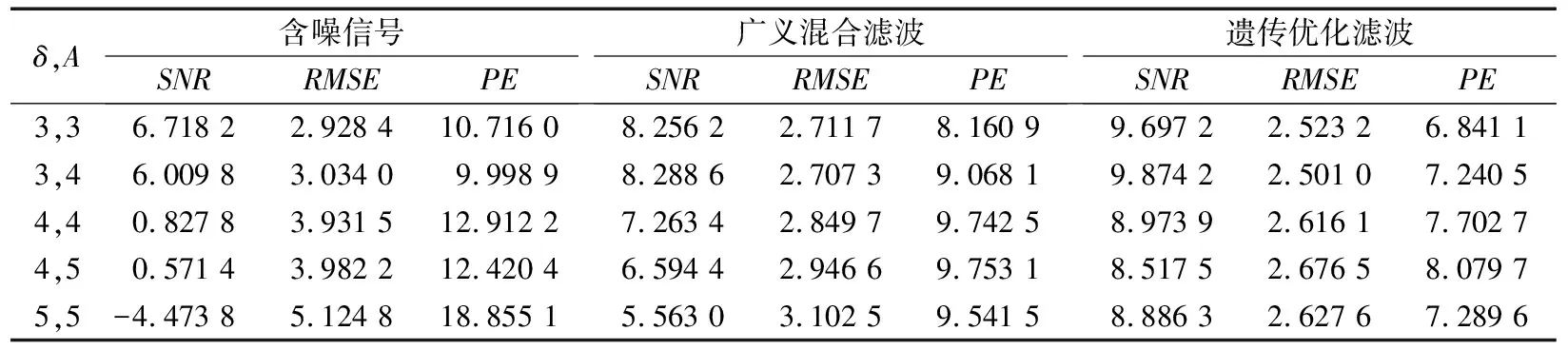
表1 各种参数下滤波效果

5 基于优化形态滤波器组、峭度和形态梯度变换的故障诊断

实测的轴承信号中，振动信号中含有以特征频率为载波，转频为调制频率的冲击成分，此时信号的峭度值将大大增强。提出一种基于优化形态滤波器组、峭度和形态梯度变化的故障诊断方法，首先采用遗传优化得到的形态滤波器组对信号滤波；而后对信号进行小波包分解后，选取峭度值最大的频段进行形态梯度变换；最后利用梯度变换有效提取出故障信号中冲击成分的优点，得到故障信号的特征频率。具体步骤如图1所示。

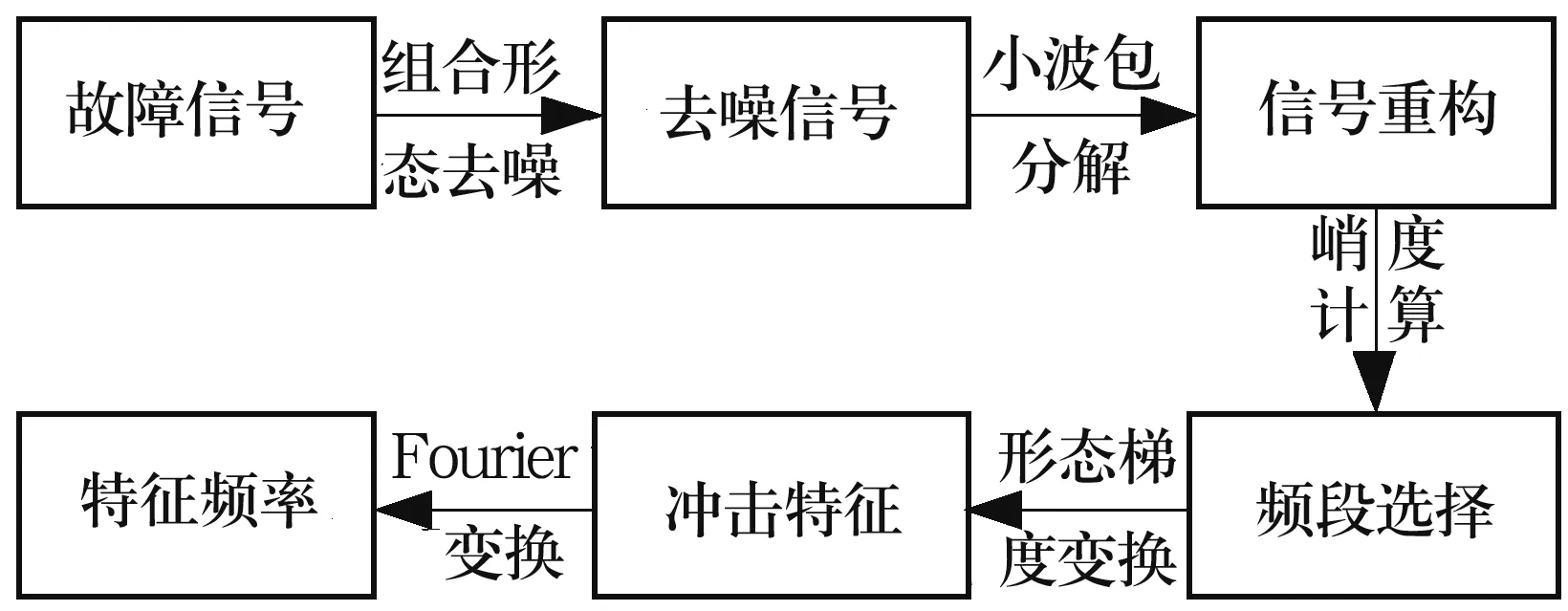
图1 故障特征频率提取流程

6 实测故障信号分析

为了检验提出的方法在故障特征提取中的效果，进行了如下试验。试验对象为KOYO1205轴承，在轴承内沟道上利用电火花加工出面积大约为3.58 mm2的点蚀。振动加速度传感器安装于故障轴承的轴承座上。在25 N·m的径向加载下，直流电动机输出转速大约为600 r/min(即fr=10 Hz)，钢球数Z=12，钢球直径Dw=7.12 mm，球组节圆直径Dpw=38.5 mm，接触角φ=0°，采样频率为48 000 Hz。经计算，内圈故障特征频率为71.1 Hz，外圈故障特征频率为48.9 Hz，钢球故障特征频率为26.1 Hz。采集信号的时域、频域分别如图2、图3所示。可以看出，由于噪声的影响，无论是时域还是频域，均无法判断有无故障。

图2 原始信号时域图

图3 原始信号的频域图

为了能够提取出轴承的故障特征，首先用组合形态滤波器组对实测信号进行滤波，而后对滤波后的信号采用db3小波基进行4层小波包分解。按照小波包系数进行重构，分别求得各频段的峭度值，如图4所示。

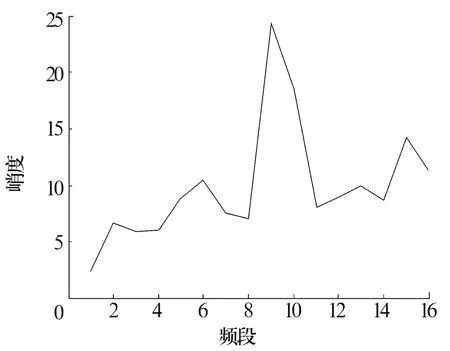
图4 分解后的各频段峭度值

由图4可知，第9频段的峭度值最大，故认为共振频率在第9频段。对重构后的第9频段进行形态梯度变换，提取其中的冲击成分，如图5所示。可以看出，冲击成分明显，具有显著的周期性。

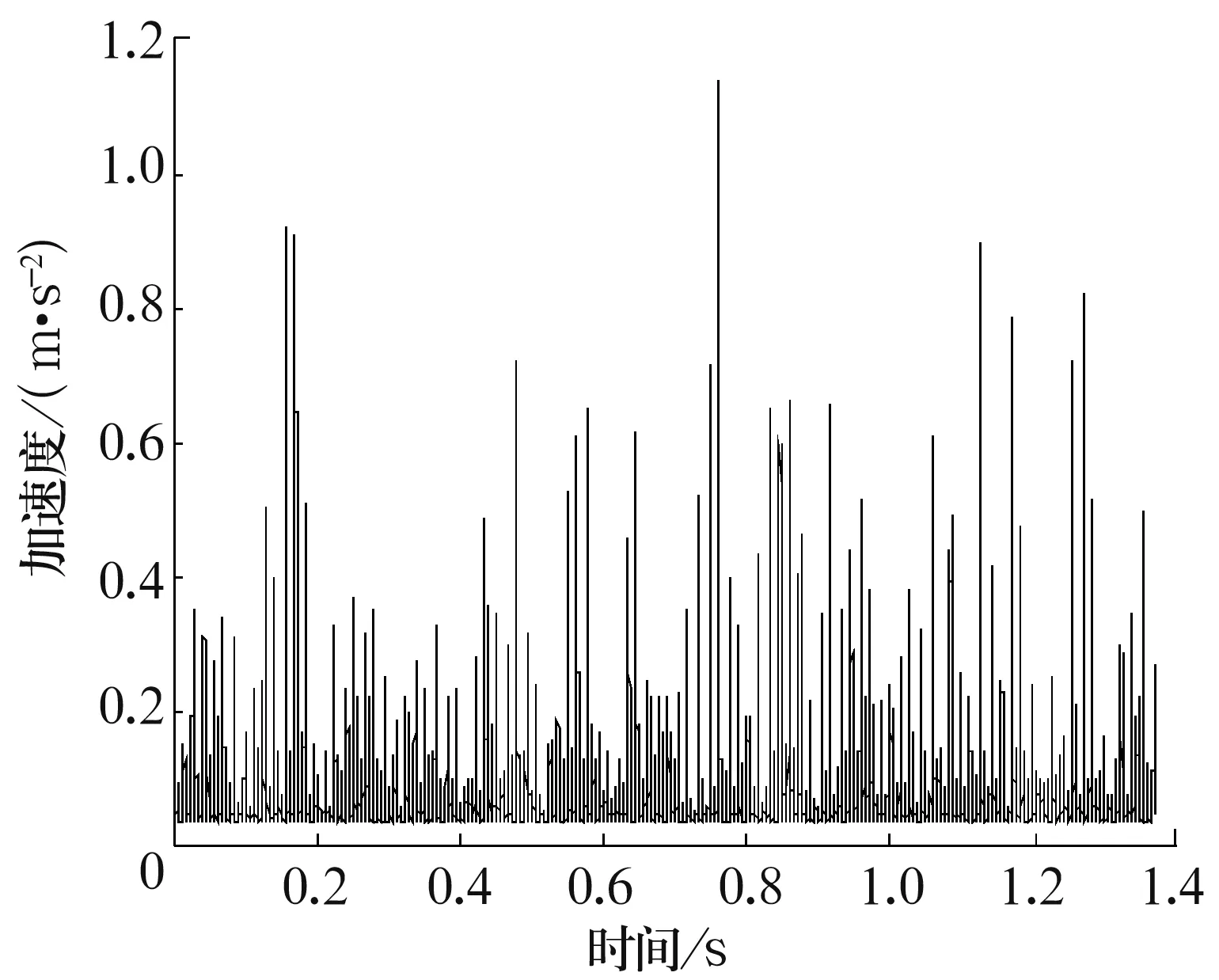
图5 冲击信号的时域图

直接对冲击成分进行Fourier变换，得到的结果如图6所示，冲击信号频域图的局部放大图(0～500 Hz)如图7所示。

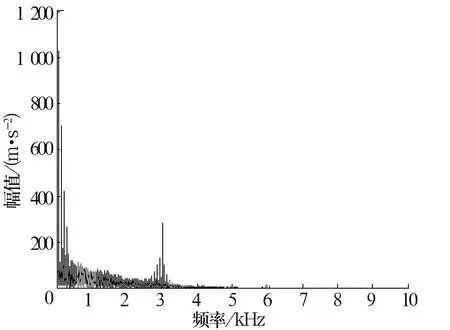
图6 冲击信号的频域图

由图7可以清晰地看出，轴的回转频率10.25 Hz、故障通过频率71.04 Hz及通过频率的2，3和4倍频。在71.04 Hz的两侧具有明显的调制信号，10.26 Hz约等于轴承的回转频率10.25 Hz。与内圈故障特征频率理论计算值基本一致，但由于钢球非纯滚动,得到的特征频率并不严格等于理论计算值。综上可以判定，轴承内圈含有故障，与实际相符，证明了该方法的有效性。

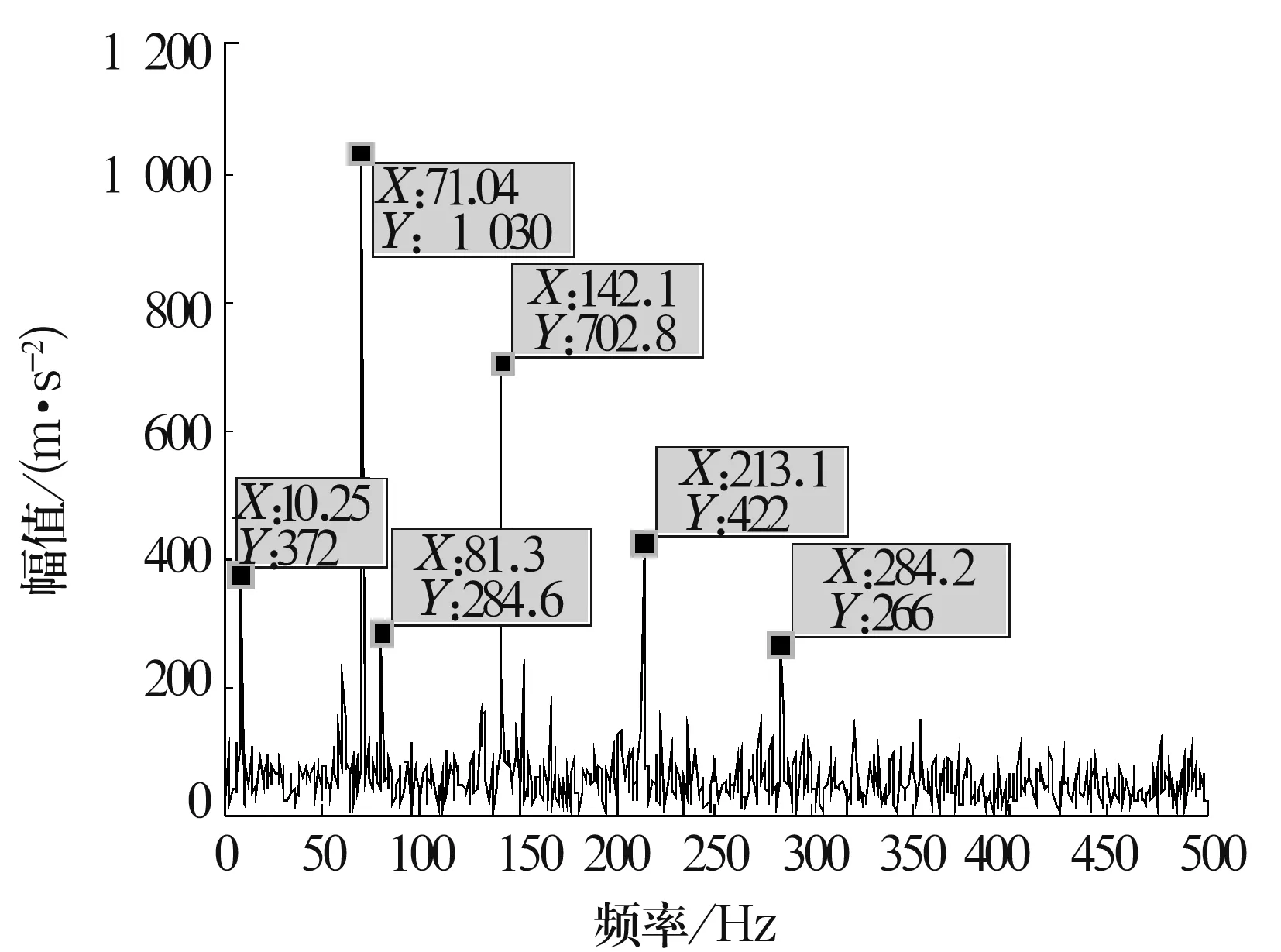
图7 冲击信号的局部放大图

7 结论

提出了结合形态滤波、小波包分解、峭度和形态梯度变换的特征提取方法，并成功应用于轴承故障诊断实例中，结果表明：

(1)遗传算法优化得到的滤波器组相对于广义组合滤波器来说，自适应地选择了结构元素和长度，因此去噪后的信号具有更高的信噪比，更低的均方根误差和峰值误差；

(2)峭度作为一个无量纲指标，用来度量机械故障的程度，能够很好地确定出共振频率所在的频段，有利于提取出冲击成分；

(3)形态梯度变换作为一种凸显信号边缘的工具，可以方便地提取出故障信号中的冲击成分。