基于EMD和排列熵的轴承异常检测方法研究

冯辅周，饶国强，张丽霞，司爱威

(装甲兵工程学院 机械工程系，北京 100072)

排列熵算法是一种新的动力学突变检测算法，能够较好地反映时间序列数据的微小变化，其应用领域也正从医学、生物、图像处理等领域延伸到机械故障诊断中[1-4]。经验模式分解(EMD)赋予了瞬时频率合理的定义、物理意义和求法，初步建立了以瞬时频率为表征信号交变的基本量，以基本模式分量为时域基本信号的时频分析方法体系[5]。通过EMD可以实现振动信号不同频带的有效分离，然后利用排列熵算法对分解后的分量进行异常检测，可以有效提高异常检测的实际效果。

1 EMD和排列熵异常检测原理

EMD通过一种“筛”的过程将任意信号分解为若干个本征模式函数(IMF)及一个余项之和，从而反映信号的内部特征。EMD不再受Fourier变换的限制，可以根据被分析信号本身的特点，自适应选择基函数对信号进行分解，自动确定信号在不同频带的分辨率，因此在分辨率上消除了小波分析的基函数选择依赖性和分析结果的模糊不确定性，具有更准确的谱结构和自适应分解特性，比较适用于非线性、非平稳的信号分析。

排列熵是一种衡量一维时间序列复杂度的平均熵参数，在反映一维时间序列复杂度的性能方面与LyaPunov指数相似，但与LyaPunov指数、分形维数等复杂度参数相比，具有计算简单、抗噪声能力强等特点[6]。该算法包括延迟时间和嵌入维数2个参数，参数的选择仍然是人为主观或凭经验确定，在此引入相空间重构的方法来对排列熵模型参数进行自适应确定，异常检测总体流程如图1所示。

图1 自适应异常检测流程图

2 轴承异常检测

采用NASA轴承试验台振动信号数据，试验装置和测点如图2所示。采样频率为20 kHz，设计了4个测点，每隔10 min采集一组数据，数据长度为20 480，共记录984组，每组数据对应一个数据文件，描述了轴承从正常工作状态到故障状态的全寿命过程信息。选取测点1处的振动加速度信号进行分析处理，如图3所示。

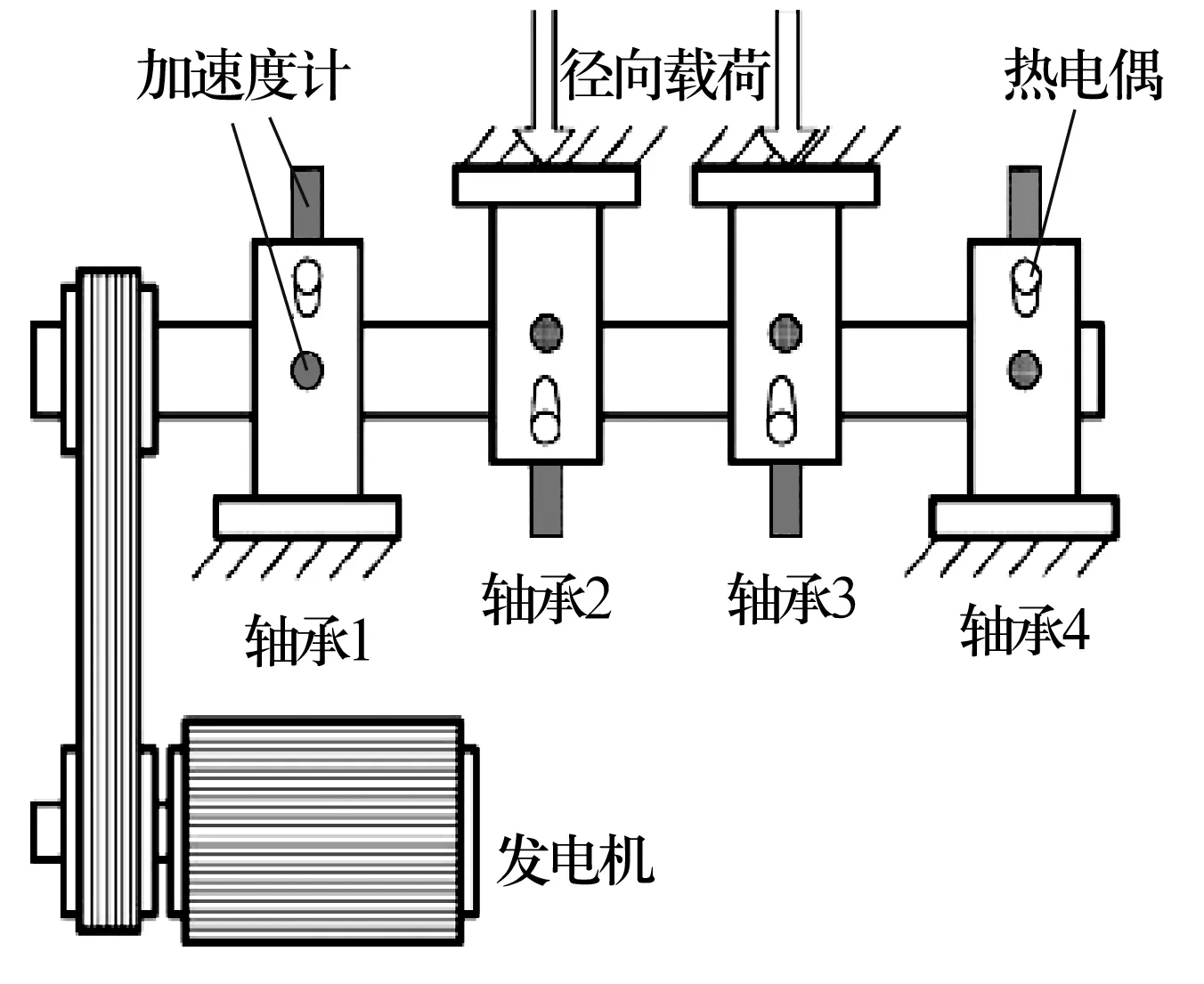
图2 轴承试验装置和测点示意图

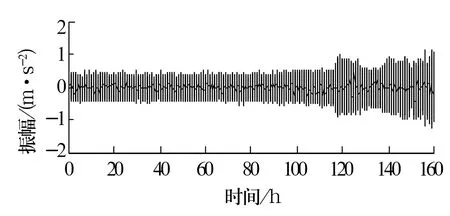
图3 测点1振动信号

2.1 EMD分解

从特征时间尺度出发，首先把信号中特征时间尺度最小的模态分量分离出来，然后分离特征时间尺度较大的模态函数，最后分离特征时间尺度最大的分量，因此可以把EMD方法看成是一组高通滤波器。

随着运行时间的延长，轴承出现异常，体现在振动信号中增加了某个频率成分，通过EMD分解可以将信号中不同频带的信号进行分离，而异常信息就有可能隐藏于某个分量当中，然后通过排列熵算法对包含异常信息的IMF分量进行分析，能够更好地检测出异常突变情况。选取长度为1 024的振动信号，如图4所示，对该段信号进行EMD分解，结果如图5所示。试验轴承为外圈故障，异常信息主要集中在高频部分，因此，主要对IMF1分量进行分析。

图4 正常信号

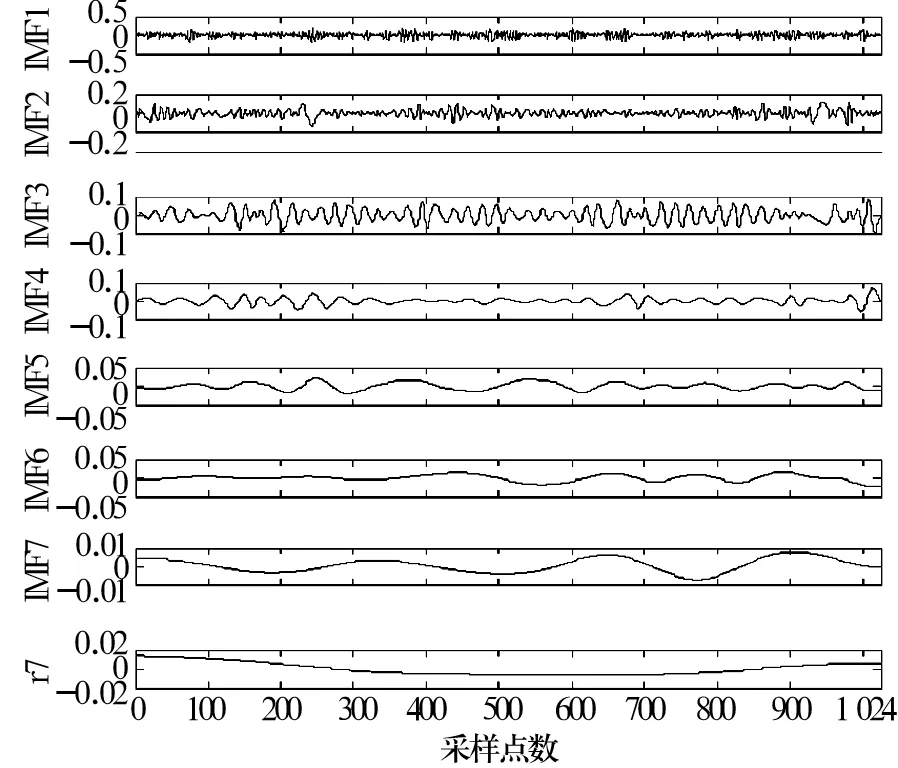
图5 EMD分解后各分量图

2.2 熵参数优化确定

延迟时间τ和嵌入维数m是排列熵算法的主要参数，对于较好地实现异常检测有一定的影响。根据排列熵算法的基本流程，对于相空间重构进行研究，采用互信息和假近邻法分别确定τ和m。

2.2.1τ的确定

自相关函数法仅能提取序列空间的线性相关性，然而互信息法包含了时间序列的非线性特征，并且计算结果远远优于自相关法，因此选取互信息法确定延迟时间τ。延迟时间取值是当互信息函数第一次达到极小值点时对应的时间。对于IMF1分量[7-8]，其延迟时间与互信息的关系如图6所示。

图6 互信息随时间延迟的变化曲线

从图6可知，当τ=1时互信息第一次取得极小值，因此延迟时间τ=1。

2.2.2m的确定

伪近邻点法表示空间数据点统计概率，其受噪声的影响相对较小。确定嵌入维数的方法是：对实测时间序列,计算虚假最近邻点的比例,然后增加m, 直到伪近邻点的比例小于5%或伪近邻点不再随着m的增加而减少时,此时对应的m为最小嵌入维数。对于IMF1分量，已知τ=1，计算得到的嵌入维数和伪近邻率之间的关系如图7所示[9-10]。判据是指判断某一空间点是否为伪近邻点的边界阈值，为了减小单一判据的不确定影响，在此选择两种判据方法作为判断是否为伪近邻点的标准。图中判据方法1选择的阈值为15，判据方法2选择的阈值为2，为了综合两种判据的效果，引入了联合判据作为m的选择依据，如图7所示，因此可确定m=4。该方法存在的不足是需要主观选择判据阈值。

图7 伪近邻率随嵌入维数的变化曲线

2.3 排列熵异常检测

对于试验测得的每组数据，首先将其分为20段，每段长度为1 024，按照异常检测的总体思路求出每段排列熵值，然后取20段的平均排列熵值作为一组数据的一个特征值，求出轴承全寿命每组数据的特征值，结果如图8所示。排列熵曲线在起始阶段有一个逐渐减小的过程，然后在一个较为平坦的区间内振荡，紧接着排列熵值出现了不同程度的下降和上升，变化速度越来越快。

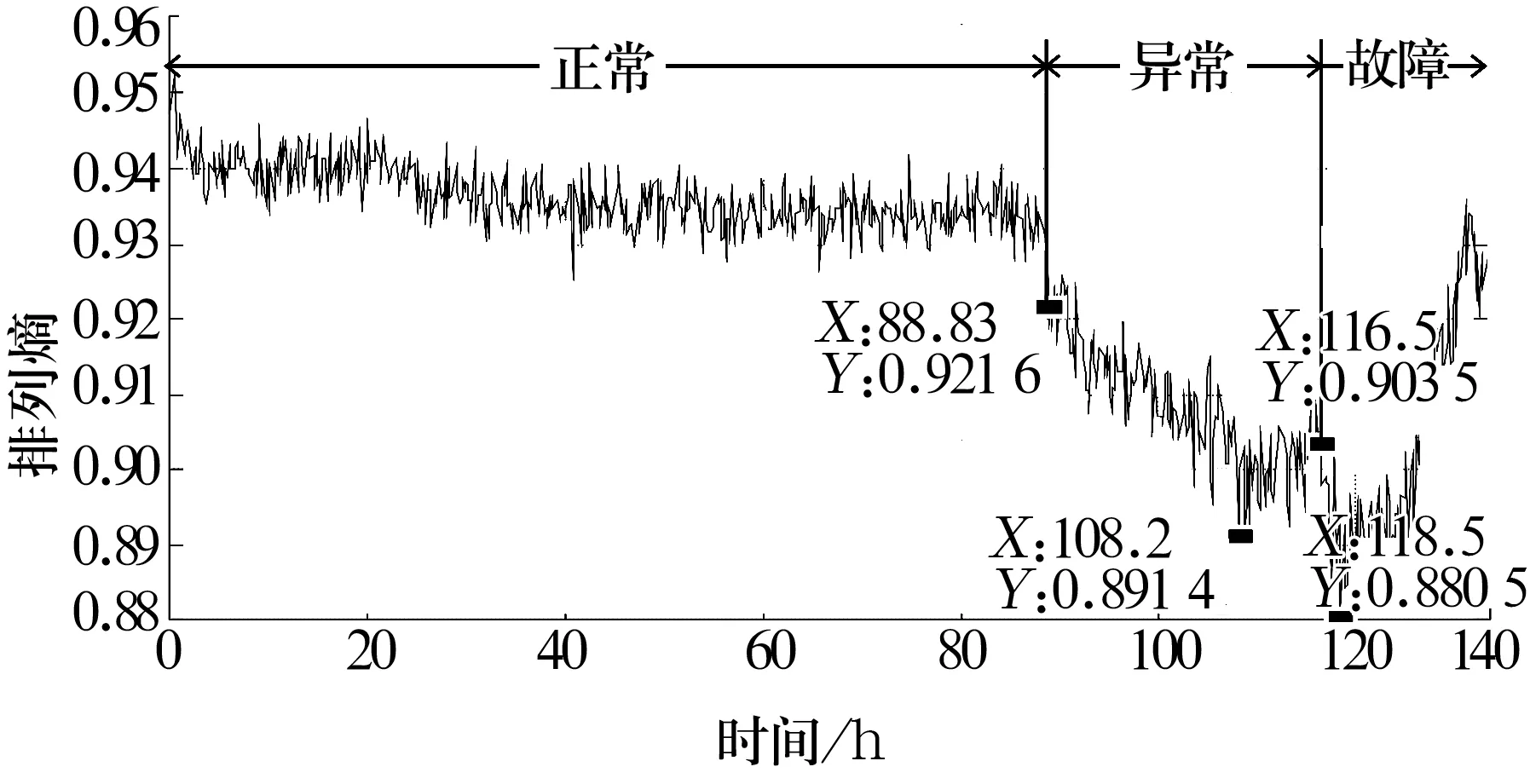
图8 排列熵变化曲线

图3所示的轴承原始振动信号在117 h左右信号幅值发生了明显的突变，对应的实际试验情况是此时轴承外圈出现了故障，但是在故障发生之前，信号没有发生明显的变化。通过排列熵特征的分析可知，特征值曲线在88.83 h以前基本在一个相对较为稳定的区段内波动，表示轴承运行正常；在88.83 h，特征值发生了明显的向下跳变，表明轴承异常开始发生；在88.83～108.2 h特征值出现整体下降，下降过程非常明显；在108.2～116.5 h段排列熵曲线出现一个稍微上升的变化，但是也基本上保持稳定；在116.5～118 h,排列熵曲线又发生明显的下降，下降幅度比较大，特征值达到最低，表明轴承故障已经发生。排列熵值的变化是由轴承运行过程中外圈从发生异常到产生故障而引起的，因此，排列熵特征对于轴承运行状态的判断具有很好的表征意义。

3 结束语

将EMD和排列熵算法相结合应用于轴承异常检测，实现了轴承运行过程中的正常、异常与故障等状态发生时刻的有效检测与区分。该方法的主要优势有：(1)异常检测的效果更加突出、明显；(2)计算过程比较简单，算法适应性好，检测效果直观明显，尤其对于机械设备在平稳运行过程中的异常在线监测，具有很好的应用前景。