加入临时路径的移动机器人路径跟踪模糊控制

孙涛，师五喜

天津工业大学 电气工程与自动化学院，天津 300387

加入临时路径的移动机器人路径跟踪模糊控制

孙涛，师五喜

天津工业大学 电气工程与自动化学院，天津 300387

1 引言

近年来，许多学者对非完整移动机器人系统的跟踪控制问题进行了大量研究[1-6]，根据参考轨迹是否为时间的函数，跟踪控制分为轨迹跟踪和路径跟踪。对于轨迹跟踪问题，文献[1-4]基于运动学模型分别提出了反步法、神经网络方法、模糊神经网络方法和输入输出线性化方法。对于路径跟踪问题，文献[5]研究了机器人质心恰好位于轮轴几何中心时的路径跟踪问题；文献[6]研究了机器人质心不在轮轴几何中心，但位于两驱动轮中轴线上时机器人的几何路径跟踪问题。众所周知，所设计的机器人最终是要有负载的，而负载的位置将直接影响整个机器人系统的质心位置，通常情况下质心位置是任意的，且其准确位置不好确定。因此文献[5-6]假设机器人质心位于轮轴几何中心或两驱动轮的中轴线上，对有负载的机器人系统是不合适的。由于质心位置不好确定，所以移动机器人系统是一类典型的不确定、非线性系统。

近年来，将神经网络与PID[7-8]、模糊逻辑系统与PID[9-11]相结合用以实现路径跟踪的控制方法层出不穷，这类方法既发挥了智能控制的灵活适应性，又利用了PID控制精度高以及控制平滑的优点，两者相得益彰，效果良好。Das等人设计的模糊控制器进一步包含了驱动器模型[12]，使其可在实际中应用。邹细勇等设计了一种分阶段模糊控制器[13]，在路径跟踪的不同阶段，采取不同的比例因子。高健等针对偏差处于不同区域（小、中、大）分别设计控制器[10]，将角度偏差范围分为小（0°～5°）、中（5°～25°）、大（25°以上）三个区域，因为在每个采样周期，1°的变化对小、中、大偏差情况有不同的影响，因此对于不同偏差范围，设计了各自的模糊控制器。该方法在不同区域设计了不同的模糊控制器，使得实时计算量偏大。

为克服以上方案的不足，本文在研究质心位置不确定的移动机器人系统几何路径跟踪问题时，引入临时路径，使机器人先从初始位置出发沿临时路径行进，当移动到期望路径附近时，再让机器人跟踪期望路径。由于机器人初始位置就在临时路径上，且只有当移动到期望路径附近时才跟踪期望路径，所以只需要针对小偏差情况设计一个模糊控制器即可，并引进积分环节以消除稳态误差。本文方法的特点是不管初始位置在何处，都可以设计出一个临时路径让机器人趋近期望路径，在小偏差范围内设计一个模糊控制器完成期望路径的跟踪。

2 移动机器人运动学模型

本文所研究的两轮差速移动机器人在直角坐标系Ox1x2中的模型，如图1所示。

图1 两轮差速移动机器人模型

该机器人前两轮为同轴独立驱动轮，轮间距为d，依靠两轮的驱动力使机器人移动，利用两轮旋转的速度差实现机器人的转向。后轮是无动力从动轮，对机器人底盘未加运动学约束，仅起到辅助支撑作用。P为两轮轴线中点，u1是P点前进速度，即机器人线速度，x3表示移动机器人相对轴x1的转角，u2=为机器人角速度，u1和u2为控制量。该坐标系中任一点以(x1，x2，x3)表示其位置和姿态。C为机器人质心，由于负载等因素的影响，一般地，质心C与P不重合，设L为点C与点P的距离，当质心位于两轮轴的前半部时，L为正，否则为负。图1中所示L为负。γ表示机器人质心C偏离中轴线的角度，假设γ∈(-π/2，π/2)。

设点C的坐标(x1，x2，x3)，由几何关系得质心C与P的位置关系为：

对上式求导并将式（1）代入，得移动机器人以质心C为参考点的运动学模型为：

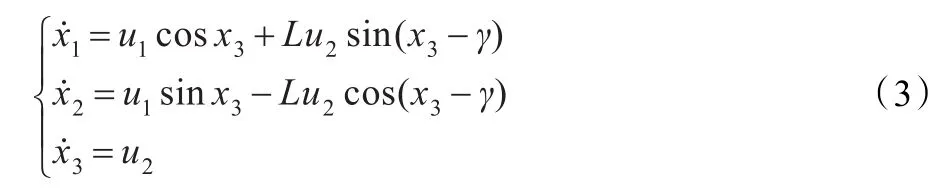
根据路径跟踪问题的提法[5]，本文的控制目标为：针对运动学模型为式（3）的移动机器人，给定光滑几何路径f(x1，x2)=0，当参数L与γ未知时，在控制量u1和u2的作用下，使其沿该给定路径运动，即对于一个任意给定的小正数δ，存在时刻t1＞0，当t＞t1时，跟踪误差z=f(x1，x2)＜δ。

为实现以上目标，本文引入临时路经，使从给定初始点出发的机器人，先延临时路径行进，当移动到期望路径附近时，再跟踪期望路径。整个跟踪过程仅需一个模糊控制器。

3 临时路径设计

本文临时路径的设计思路如下，为研究问题方便，文中只对期望路径为直线和圆的情况进行了研究。

若期望路径为直线，如图2，P(x10，x20)为初始位置，期望路径为直线f(x1，x2)=kx1-x2+b=0，临时路径设计为以Ot(x1t，x2t)为圆心，半径为Rt的圆。

图2 期望路径为直线的临时路径设计

P点到期望直线距离的一半为临时圆的半径，即

临时圆圆心Ot位于垂直于跟踪直线且过P点的直线上，该直线方程为：

另外，圆心到直线距离为Rt，通过以下联立方程：

可解得临时圆圆心。

若期望路径为圆且初始点在圆外，如图3，P(x10，x20)为初始位置，期望路径为圆f(x1，x2)=(x1-x1r)2+(x2-x2r)2-R2=0，临时路径设计为过P点的圆的切线ktx1-x2+bt=0。

图3 期望路径为圆且初始点在圆外的临时路径设计

期望圆圆心到该切线距离等于半径且切线过P点，通过以下联立方程：

可解得切线方程。

若期望路径为圆且初始点在圆内，如图4，P(x10，x20)为初始位置，期望路径为圆f(x1，x2)=(x1-x1r)2+(x2-x2r)2-R2=0，临时路径设计为以Ot(x1t，x2t)为圆心、半径为Rt的圆。

图4 期望路径为圆且初始点在圆内的临时路径设计

临时圆的半径等于期望圆的半径减去OP两点距离的一半，即

临时圆圆心Ot在OP两点确定的直线上，该直线方程为：

解得临时圆圆心。

当设计完临时路径后，在小偏差范围内就可以设计模糊控制器了。

4 模糊控制器设计

模糊控制器采用常见的控制器，以跟踪误差z和误差变化率z˙为输入，以机器人角速度u2（控制器中以u表示）为输出。这种双输入单输出结构的模糊控制器具有非线性PD控制规律，利于保证系统的稳定性，减少超调，削弱振荡现象，动态性能好；线速度u1设为一常值。

通常在实施模糊控制时，由于论域划分的有限性，控制效果不够精细，存在一定的稳态误差。虽然通过论域细分，可以在一定程度上减小稳态误差，但无法消除，且增加了控制器设计的复杂性。本文引入积分环节，可在不增加控制规则的基础上，有效提高控制精度。本文方案中的模糊控制相当于粗调，积分环节相当于细调，两者结合，既保留了模糊控制良好的动态特性，又利用了积分环节的特点消除系统的稳态误差，控制器设计简单有效，其结构图如图5。

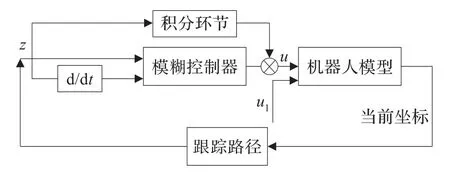
图5 模糊控制系统结构图

对模糊控制器的两输入变量各定义7个模糊集合：NB、NM、NS、ZO、PS、PM、PB，对输出变量定义7个模糊集合：LB、LM、LS、ZO、RS、RM、RB，论域皆设为[-3，3]。

模糊控制实践表明，隶属函数曲线的具体形状，取为三角形、梯形还是正态分布形，对控制器性能影响不大，而各模糊子集隶属函数对论域的覆盖面积以及控制器特性有一定影响。面积越小，分辨率则越高，引起的输出变化大，控制灵敏度高，反之灵敏度低。当偏差较大时采用低分辨率隶属函数，输出平稳，当偏差较小或接近零时采用高分辨率函数，对误差及时反应。

本文设计的控制器基于小误差情况，因此采用全交迭三角形隶属度函数，如图6和图7所示。采用此类隶属度函数，分辨率高，可以对误差快速反应，且能有效降低计算量，增加系统鲁棒性。

图6 输入变量隶属度函数

图7 输出变量隶属度函数

根据人工驾驶经验获得模糊控制规则，如表1所示。

表1 模糊控制规则

5 仿真结果

图8 跟踪直线情况

对于式（3）的机器人运动学模型，取重心参数L=-0.3 m， γ=π/6，线速度u1=0.3 m/s，采样周期0.01 s，使用Matlab进行仿真。

期望路径为直线x2=0即x1轴，机器人初始点（0，-4，5π/6），临时路径设计为圆x12+(x2+2)2-4=0。输出量为角速度，论域为[-3，3]，而实际角速度不可能过大，因此比例因子设为1/6，即将输出量限制在[-0.5，0.5]之间，符合实际情况，并引入积分环节消除静差。跟踪结果如图8所示。

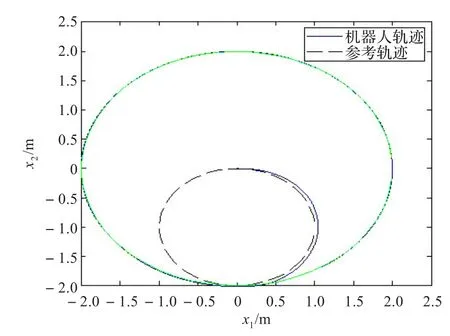
图10 初始点在圆内时跟踪圆情况

图9 初始点在圆外时跟踪圆情况

从跟踪过程可以看出，机器人从初始位置出发，先跟踪设计的临时路径，当移动到期望路径附近时，跟踪路径切换到期望路径，完成整个跟踪，其中的路径切换平稳迅速，在跟踪过程中引入了积分环节，消除了稳态误差，且无振荡现象，效果良好，验证了该方法的有效性。

6 实验结果

6.1 实验条件

本文以上海英集斯自动化技术有限公司的智能机器人MT-AR为平台进行实验。该机器人为轮式结构，前两轮为同轴驱动轮，后侧配一万向轮起平衡支撑作用，其模型与文中研究的机器人模型一致。图11为机器人系统及实验场地。

图11 实验用机器人及实验场地

该机器人由上位机、驱动系统和电机三部分组成。

上位机为工业级计算机，实现人机交互，通过串口与下位机通讯，发送命令和反馈信息。

驱动系统核心采用TI公司的DSP芯片TMS320LF2407，作为一种专门针对控制领域而开发的高性能16位定点DSP芯片，具有功耗低，响应快，集成度高的特点，尤其在电机控制方面优势明显。

实验过程中，通过程序控制DSP输出两路PWM信号分别控制左右电机，信号经6N137高速光耦，与之后的模拟驱动电路隔离。驱动电路采用IR2110加单极性H桥电路的结构，IR2110开关速度快，输入及输出电压几乎无相位滞后，且功耗较低。单极性H桥电路实现电机正反转，需正确配置死区定时器以防止H桥电路击穿。两电机各装一只500线增量式光电编码器，正交编码脉冲单元可对其输出的脉冲信号进行鉴相和四倍频，实时反馈电机转速，以便进行下一步控制。

电机为两只空心杯转子直流电机，加速平稳，电磁干扰小，效率高。减速箱为二级减速，减速比33∶1。

6.2 实验方案

首先根据模糊规则建立7行7列的模糊控制表，存于DSP内存中，如表2所示。

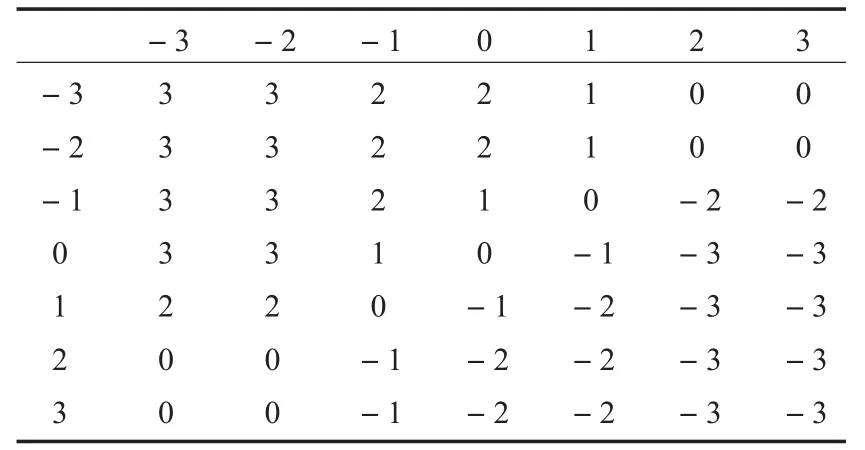
表2 模糊控制表

针对两轮差速驱动机器人有：

其中，u1表示机器人的线速度，这里设为常值0.3 m/s；u2表示机器人的角速度即模糊控制的输出u；vr表示机器人右轮速度；vl表示机器人左轮速度；d表示两轮间距，实验值为401 mm。

机器人坐标按下式计算：

其中，x1，i、x2，i和x3，i分别是移动机器人在ti时刻的横坐标、纵坐标和其与x轴正向夹角，x1，i+1、x2，i+1和x3，i+1分别是移动机器人在ti+1时刻的横坐标、纵坐标和其与x轴正向夹角。

程序设计中首先对系统初始化，其中EVA和EVB的初始化是关键，包括设置EVA的T1定时器用于产生中断，中断时间0.1 s，T2定时器用于左电机编码器计数，EVB的T3定时器产生两路PWM控制左右电机，T4定时器用于右电机编码器计数。为实现路径跟踪，每次中断时由编码器返回两轮转速，按式（8）计算机器人当前位置，计算误差和误差变化率，经模糊化转化为模糊量，按该模糊量查询规则表，获得模糊输出量，再乘以比例因子，最终得到调整后的角速度；由式（7）计算相应的vr和vl，据此改变比较寄存器的值，用调整后的PWM控制电机，最终实现路径跟踪。

6.3 实验结果

实验参数同仿真以观察跟踪效果。取重心参数L=-0.3 m，γ=π/6，线速度u1=0.3 m/s，中断周期0.1 s，所得实验数据导入Matlab画图，同仿真进行对比。

期望路径为直线x2=0即x1轴，初始点为(0，-4，5π/6)时，临时路径设计为圆+(x2+2)2-4=0。跟踪结果如图12所示。

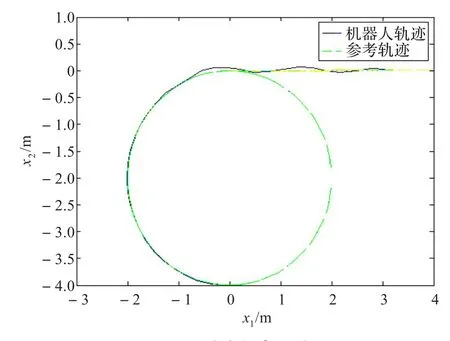
图12 跟踪直线实验情况

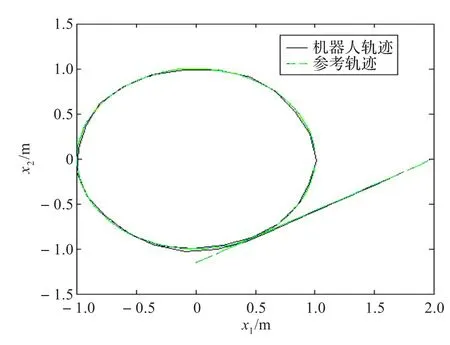
图13 初始点在圆外时跟踪圆实验情况

由实验结果看出，整体运行效果与仿真结果基本一致，跟踪路径切换平稳。实验结果令人满意，验证了本文算法的有效性。

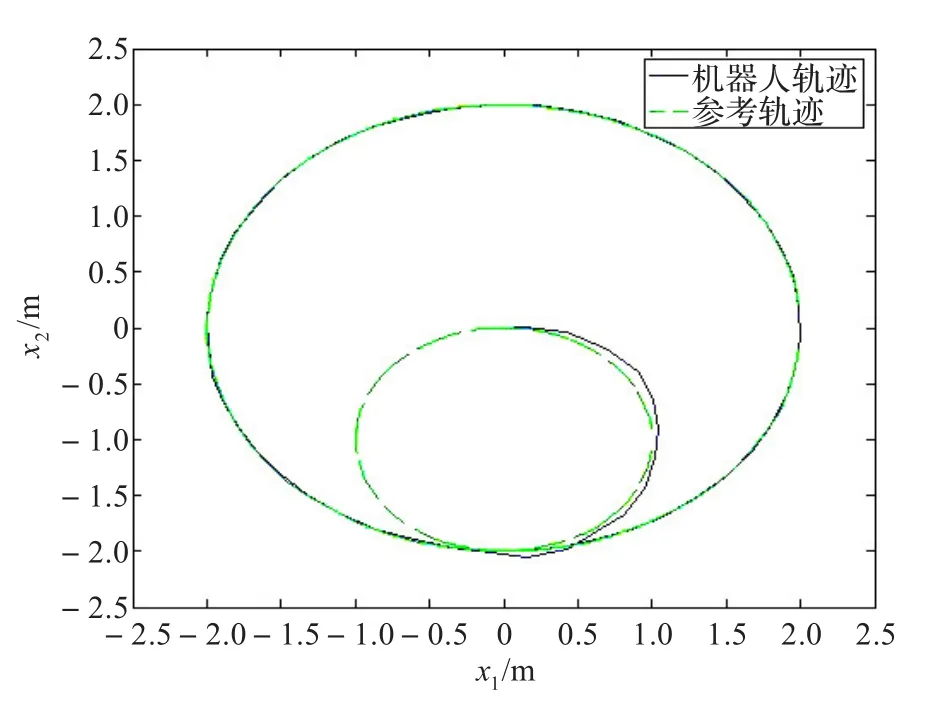
图14 初始点在圆内时跟踪圆实验情况

7 结论

对于移动机器人路径跟踪问题，在建模时一般都假定其重心在某一位置，而实际上重心位置跟其结构有关，是不确定的，在机器人负载后还会变化，因此本文针对重心位置任意的机器人建立模型，采用模糊控制方法实现路径跟踪控制，并加入积分环节以消除静差。在模糊控制器设计中，需要针对机器人位置或角度误差范围设计多个控制器，方法过于复杂且计算量偏大，本文引入临时路径思想，设计一个模糊控制器即可完成任意初始位置的路径跟踪。针对直线与圆的仿真和实验结果表明，本文方法简单有效，跟踪效果良好。当期望路径为其他光滑曲线方程时，通常设计临时路径为过初始点且与该期望路径相切的直线或圆弧，通过平面解析几何知识中的曲线位置关系，结合已知条件解得临时路径方程。

[1]Kanayama Y，Kimura Y，Miyazaki F，et al.A stable tracking controlmethodforanautonomousmobilerobot[C]//ProceedingsofIEEEInternationalConferenceonRobotics and Automation，Cincinnati，OH，USA，1990：384-389.

[2]Yuan G，Yang S X，Mittal G S.Tracking control of a mobile robot using a neural dynamics based approach[C]//Proceedings of IEEE International Conference on Robotics and Automation，Seoul，South Korea，2001：163-168.

[3]Hu Y，Yang S X.A fuzzy neural dynamics based tracking controller for a nonholonomic mobile robot[C]//Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics，Kobe，Japan，2003：205-210.

[4]Kim D H，Oh J H.Tracking control of a two-wheeled mobile robot using input-output linearization[J].Control Engineering Practice，1999，7（3）：369-373.

[5]马保离，霍伟.移动机器人的路径跟踪问题[J].机器人，1995，17（6）：359-362.

[6]孙多青，霍伟，杨枭.含模型不确定性移动机器人路径跟踪的分层模糊控制[J].控制理论与应用，2004，21（4）：489-500.

[7]Fierro R，Lewis F L.Control of a nonholonomic mobile robot using neural networks[J].IEEE Transactions on Neural Networks，1998，9（4）：589-600.

[8]Ge S Z，Wang C.Direct adaptive NN control of a class of nonlinear systems[J].IEEE Transactions on Neural Networks，2002，13（1）：214-221.

[9]李啸，张洪钺，李骥.基于模糊PID的轮式移动机器人轨迹控制[J].机器人技术与应用，2002（5）：30-33.

[10]高健，黄心汉，彭刚，等.基于Fuzzy-PID的移动机器人运动控制[J].控制工程，2004，11（6）：525-528.

[11]徐建安，邓云伟，张铭钧.移动机器人模糊PID运动控制技术研究[J].哈尔滨工程大学学报，2006，27（B07）：115-119.

[12]Das T，Kar I N.Design and implementation of an adaptive fuzzy logic-based controller for wheeled mobile robots[J]. IEEE Transactions on Control Systems Technology，2006，14（3）：501-510.

[13]邹细勇，徐德，李子印.非完整移动机器人路径跟踪的模糊控制[J].控制与决策，2008，23（6）：655-659.

SUN Tao,SHI Wuxi

School of Electrical Engineering and Automation,Tianjin Polytechnic University,Tianjin 300387,China

A fuzzy control scheme of path tracking for mobile robots with uncertainty is presented.A temporary path is designed for the path tracking,which makes the robot move along the designed temporary path first,when it is near the desired path,the robot will go along it then.The whole tracking process is controlled by one fuzzy controller,which reduces the computation burden, and an integration term is added into the controller to eliminate the steady-state error.The performance of proposed approach is demonstrated through simulation and experiment examples.

temporary path;tracking control;fuzzy control

对含不确定性的移动机器人系统设计了路径跟踪模糊控制方法。该方法引入临时路径，使机器人先从初始位置出发沿临时路径行进，当移动到期望路径附近时，再让机器人跟踪期望路径。整个控制过程只需要一个模糊控制器，极大地减少了工作量，并引进积分环节以消除稳态误差。仿真和实验结果验证了该方法的有效性。

临时路径；跟踪控制；模糊控制

A

TP242.6

10.3778/j.issn.1002-8331.1110-0605

SUN Tao,SHI Wuxi.Fuzzy control for path tracking of mobile robots with temporary path.Computer Engineering and Applications,2013,49（13）：228-233.

天津市自然科学基金（No.10JCYBJC07400）。

孙涛（1986—），男，硕士研究生，主要研究领域为移动机器人智能控制；师五喜（1964—），男，博士，教授，主要研究领域为智能控制。E-mail：suntao30920@163.com

2011-11-02

2012-01-30

1002-8331（2013）13-0228-06

CNKI出版日期：2012-03-21http://www.cnki.net/kcms/detail/11.2127.TP.20120321.1738.051.html