复杂调制形式脉压雷达信号的识别方法

李建，张国毅，王长宇

空军航空大学 航空信息对抗系，长春 130022

复杂调制形式脉压雷达信号的识别方法

李建，张国毅，王长宇

空军航空大学 航空信息对抗系，长春 130022

1 前言

为了解决探测距离与探测精度之间的矛盾，许多雷达都采用了脉冲压缩技术。要实现脉冲压缩，就必须对雷达信号进行脉内调制，早期的脉压雷达一般采用线性调频和二相编码。然而，为了提高自身的生存概率，如今的脉压雷达采用了各种复杂的调制形式，例如：正弦调频、频率编码和多相编码等，这给电子对抗雷达侦察带来了非常大的挑战。

近年来，针对复杂调制形式脉压雷达信号的识别问题，相关研究人员提出了很多方法。文献[1]提出针对低截获概率雷达信号的识别方法，但该方法识别的类型有限且分类特征并不明显；文献[2]提出了结合AR模型功率谱估计分析法和小波变换模极大值法的识别方法，能在0 dB时，较好地实现对相位编码、频率编码和简单的脉内混合调制类型的雷达信号的识别，但该方法的步骤繁多且无法识别多相编码等信号；文献[3-4]分别提出一种基于核Fisher判别分析（KFDA）的数字调制信号分类器的设计方法和一种基于多频带能量算子的FSK信号分类方法，这两种方法主要针对通信类的信号，识别的调制类型有限。要满足现代电子对抗雷达侦察的需要，识别方法需要具备以下的特性：（1）能识别主流的复杂脉压雷达调制信号；（2）能提取出较明显的分类特征，方便人工校验；（3）有较强的抗噪声性能。而以上研究提出的方法均无法全部满足这些要求。

为此，提出一种能完成对线性调频（LFM）信号、正弦调频（SFM）信号、频率编码（2FSK、4FSK）信号、多相编码（Frank码、P1～P4码）信号和二相编码（BPSK、QPSK）信号进行识别的方法。该法通过对信号的ZAM-GTFR进行Radon变换，提取最佳旋转角将信号分为两类信号：第一类为时频脊线具有一定倾斜角的信号，包括LFM、Frank码信号和P1～P4码信号；第二类为时频脊线平行时间轴的信号，包括BPSK、QPSK、2FSK、4FSK和SFM信号。通过提取最佳旋转角对应的信号ZAM-GTFR的Radon变换的模值中满足一定条件的尖峰数，将两大类信号区分开。仿真结果表明，该方法能在-3 dB下达到94%的平均正确识别率。

2 信号模型

脉压雷达信号按调制形式可分为相位调制、频率调制和混合调制信号。但无论哪种调制形式，其数学表达式都可以表示为[5]：

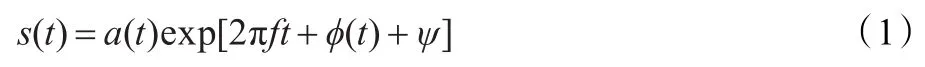
其中，a(t)为脉冲信号的幅度包络：a(t)=Arect(t/T)，A为脉冲幅度，T为脉宽，f为信号的载频，ϕ(t)为调制编码函数，ψ为初相。不同的调制形式主要体现在ϕ(t)上，每一类信号具体的ϕ(t)表达式详见文献[5]。

本文主要识别的调制类型有频率调制中的线性调频（LFM）信号、正弦调频（SFM）信号和频率编码信号（2FSK和4FSK）；相位编码中的二相编码（BPSK）、四相编码（QPSK）信号和多相编码（Frank码和P1～P4码）信号。它们在现代脉冲压缩雷达中得到了广泛的应用[6]，研究识别这些信号的方法有重要的意义。

3 ZAM-GTFR时频法与Radon变换原理

3.1 ZAM-GTFR时频法原理

现代脉压雷达采用的调制形式具有时变的特点且峰值功率越来越低，分析这种信号二次时频分析工具有着非常好的效果。在二次时频分析工具中，Wigner-Ville Distribution（WVD）具有最高的时频聚集性，非常适合分析线性调频类调制信号。然而它却存在较强的交叉干扰项，这种特性导致WVD在分析具有非线性时频特点的信号时性能不佳。为解决这个问题，研究人员提出了基于核函数的改进法。总的说来这些方法可分为固定核法[7]和自适应核法[8]。自适应核法需要在不同的时间自适应选择不同的窗函数，这种方法太过复杂难以实现。固定核法虽然具有稍差的时频聚集精度，但这同时换来了较强的抗噪声性能，同时也能明显区分各类调制信号。在固定核法中，ZAM-GTFR法具有较高的时频聚集性、抗噪声性能和较低的交叉项[9]。因此，该方法具有较强的通用性，既能在分析线性类调频信号时拥有较高的时频聚集度，又能在分析非线性类调频信号时避免交叉项的干扰。另外，该方法作为时频分析工具的一种能够在低信噪比下提取时变信号的瞬时频率，给情报分析人员提供了直观的识别特征，能够满足识别中人工校验的要求。

基于上述分析，本文将其作为分类的变换工具。若信号为x(t)，其ZAM-GTFR表达式如下[9]：

其中，*表示取共轭，g(τ)表示窗函数，A(t，τ)表示t时刻的自相关函数。

为了在计算机上实现该算法需要对其进行离散化，离散的ZAM-GTFR表达式如下：

其中，m≤L，M=2L+1。

图1给出了在5 dB的条件下，分别利用WVD和信号的ZAM-GTFR对正弦调频信号进行处理的结果。

图1 正弦调频信号的时频特征

从图1中可知，在分析正弦调频信号时，ZAM-GTFR有着较强的抗噪声性能和较小的交叉项。它的时频聚集性虽然比WVD低，但其特征明显足以区分出信号的类型。

3.2 Radon变换原理

Radon变换是一种直线积分投影变换，它是图像处理技术中一种用于检测直线的有力工具。任意二维函数f(t，ω)的Radon变换定义为[10]：

图2给出了Radon变换的原理示意图。

图2 Radon变换坐标关系图

如图2所示，将原直角坐标旋转α角度得到新的直角坐标(u，v)，以不同的u轴平行于v轴积分，得到的变换就是Radon变换。由此可知直线斜率k=-cotα。

根据坐标旋转公式可以得到这两个坐标系之间的关系：

4 信号识别原理

4.1 基于斜率的信号分类

根据信号的斜率，把Frank码、P1～P4码信号和LFM信号分为第一类；把SFM、2FSK、4FSK、BPSK和QPSK信号分为第二类。

多相码编码中的Frank码、P1码和P2码衍变于步进频率，P3码和P4码来自线性频率，因此，这几种多相码的时频特征类似线性调频信号。LFM信号和多相编码信号在时频面上呈现出一条或数条时频脊线，如图3所示。

线性调频信号的时频脊线斜率可正可负；多相编码信号中除了P2码信号时频脊线的斜率为负外，其他几种编码信号的均为正。据此，这一类信号可归类为具有一定倾斜角的信号。

正弦调频信号、频率编码信号和相位编码信号的ZAM-GTFR的时频脊线都是平行于时间轴的，如图4所示。

如图4（a）所示，频率编码信号的时频图呈现出数条平行横轴的时频脊线。如图4（b）所示，相位编码信号基本呈现出一条直线，只是不同的编码呈现出一定的小毛刺。理论上，正弦调频信号在时频面应该是一条曲线。然而，如图4（c）所示，经过ZAM-GTFR变换后的结果却是在正弦曲线的波峰和波谷有着非常高的能量，在曲线的其他地方能量较低，时频脊线近似平行于时间轴。总的说来，这几种信号的时频脊线都可归类为倾斜角为零的信号。

根据以上分析，可以基于斜率将信号分为两大类。而区分这两大类信号，时频脊线倾斜角的计算是关键。Radon变换是有效的直线检测工具，它能在图像的倾斜角方向取得最大的信号能量积累，积累的过程也是对随机起伏噪声的抑制。因此，本文利用Radon变换来提取信号的ZAM-GTFR中时频脊线的倾斜角。为了方便表述，下文将信号ZAM-GTFR的Radon变换简写为RZT。图5给出了0 dB条件下信号RZT在不同旋转角度下的模极大值。

图5中横坐标的角度是Radon变换的旋转角，图中峰值对应的旋转角被称为最佳旋转角。由图5可知，第一类信号最佳旋转角不为90°，第二类信号的最佳旋转角均为90°。而Radon变换的旋转角和信号的倾斜角是互为余角的。因为第一类信号的时频脊线具有一定倾斜角，所以其最佳旋转角不为90°；因为第二类信号时频脊线的倾斜角为零，所以其最佳旋转角为90°。因此，只要判断信号RZT的最佳旋转角θ是否为90°，即可将两类信号分开。

按如下方法将两大类信号分开：若θ在85°～95°之间，则将信号判为第二类信号；否则判为第一类信号。为了提高算法的抗噪性，本文采用中值滤波器对Radon变换后的结果作一定的平滑以消除毛刺。

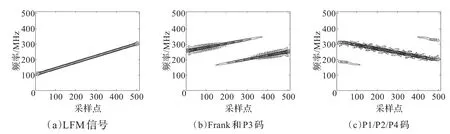
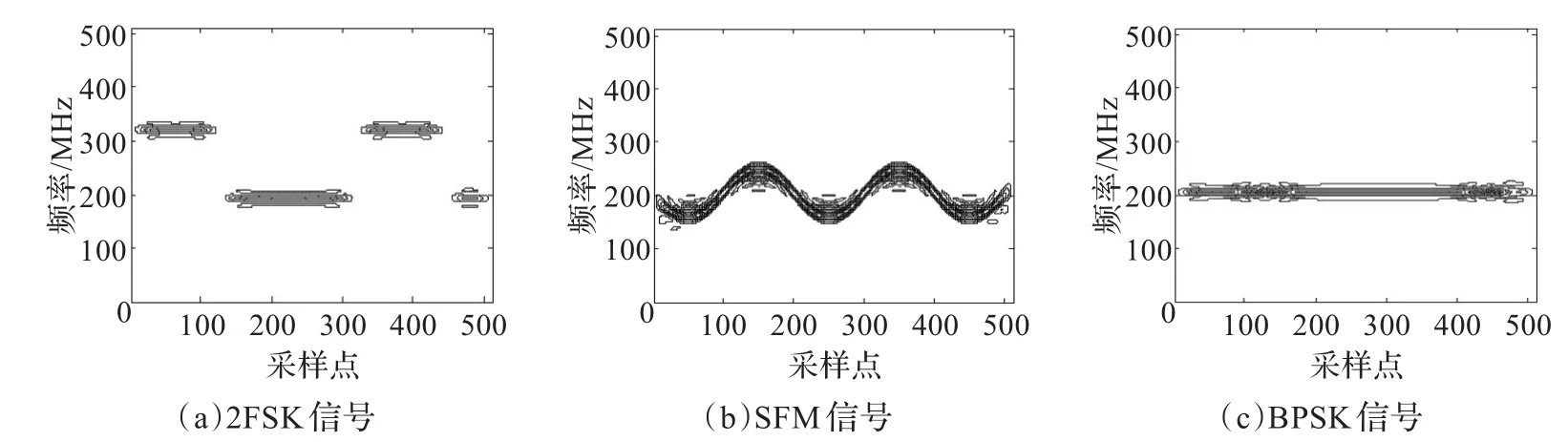
图4 第二类信号的ZAM-GTFR

图5 信号RZT在不同旋转角的模极大值

图6 最佳旋转角对应的信号RAT的模值

4.2 对第一类信号的分类

该步骤主要完成多相编码信号和LFM信号的分类。如图3所示，在经过ZAM-GTFR变换后，Frank码、P3码信号与P1码、P2码、P4码和LFM信号在时频特征上有一定的差异，但P1/P2/P4码信号和LFM信号在低信噪比条件下区分不明显。

经过大量仿真实验后发现，多相编码信号和LFM信号在经过RAT（Radon-Ambiguity Transform）[11]后具有比较明显的区分特征。图6给出了0 dB条件下信号在最佳旋转角度的RAT的模值。

如图6所示，多相编码信号和LFM信号经过RAT后具有了明显的区分特征。多相编码信号最佳旋转角对应的RAT的模值图呈现出数条平行的时频脊线，而LFM信号的只有一条脊线。另外，AF（Ambiguity Function）可看做信号自相关函数的傅里叶变换。计算AF可以利用ZAM-GTFR的中间结果，不会增加过多的计算量[9]。

如图6所示，多相编码信号和LFM信号的最大区别就在于其RAT的主脊线两侧对称的存在两处明显的副脊线。通过大量仿真实验，本文发现理想的多相编码信号RAT的副脊线峰值与主脊线峰值的比值是固定的，如表1。

表1 最高峰值与次高峰值之比

因此，可以通过判断其RAT的明显的脊线条数来区分无噪声条件下的多相编码信号和LFM信号。设定阈值λ，令其略小于表1中的0.35（本文取0.32），搜索大于λ的尖峰数C，若C大于1判为多相码；否则判为LFM信号。仿真发现，这种方法仅在较高信噪比时适用，一方面，随着信噪比不断下降，LFM信号RAT的基底越来越强，噪声极易超过阈值λ，从而导致信号类型的错判；另一方面，多相编码信号的基底也不断增强，副脊线的值也逐渐超过表1中的值，在噪声中露出来。利用副脊线对称分布于主脊线的特点，本文修正了仅利用阈值λ进行分类的方法，将其改为：在超过阈值λ的尖峰中，搜索最高峰两侧的次高峰并确定其相对最高峰横坐标的位移d1和d2，若d1/d2范围在[0.9，1.1]，则保持C的取值；反之，将C改为1。

对于不同码型的多相码编码信号的区分采用如下规则。根据3.1节中的斜率分析，将θ大于95°的多相编码信号判为P2码信号。剩下的Frank、P1、P3和P4码信号，则依据次高峰与最高峰的峰值之比R进行分类。当信号被判为多相编码信号后，求最高峰两侧的次高峰值的平均值，计算其与最高峰值之比R。若R大于0.7，则判为Frank/P3码信号；若R小于0.7，则判为P1/P4码信号。

但是本文方法无法细分Frank/P3码以及P1/P4码信号，本文还未找到有效区分Frank码和P3码信号，P1码和P4码信号的特征。

4.3 对第二类信号的分类

该步骤完成对BPSK/QPSK信号、2FSK/4FSK信号和正弦调频信号的分类。这几种信号的ZAM-GTFR的时频特征详见2.1节。鉴于几种信号在时频图上的特征，本文利用信号RZT在最佳旋转角的模值进行分类。信号的ZAM-GTFR经过Radon变换后既积累了信号能量，让信号的真实时频脊线得以呈现，又能利用噪声随机变化的特点减小了噪声的幅度。此外，为进一步减少噪声的影响，采用中值滤波器对积累后的结果进行一定的平滑处理。图7给出了0 dB条件下信号RZT在最佳旋转角度的模值。

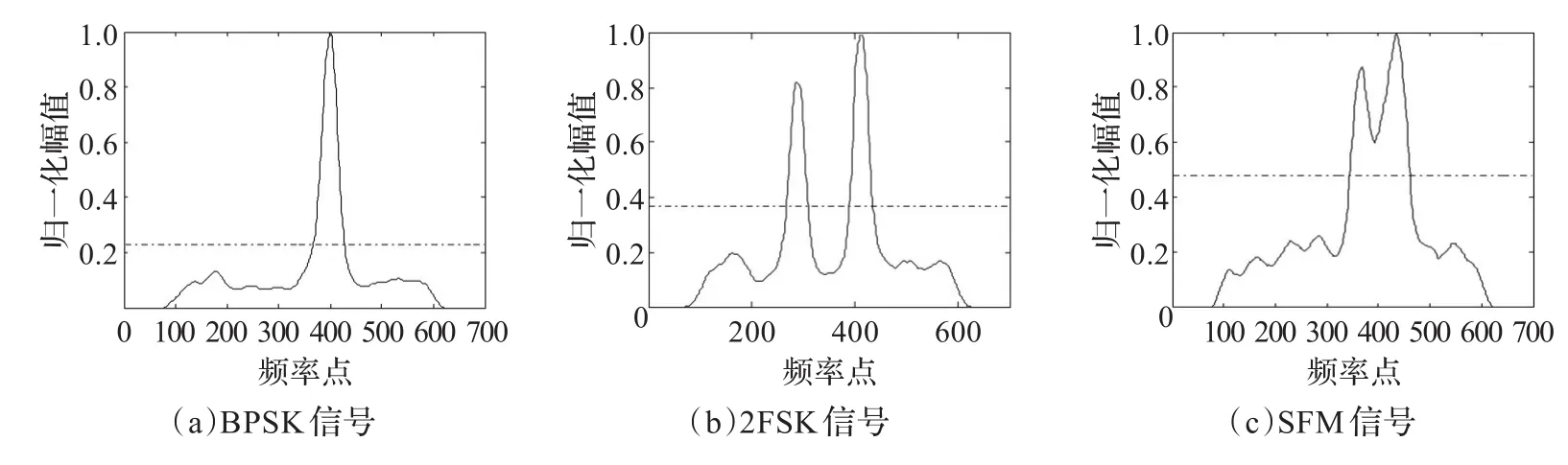
图7 最佳旋转角对应的信号RZT的模值

如图7（a）所示，BPSK/QPSK信号在经过上述处理后在其载频处出现了非常明显的尖峰。如图7（b）所示，2FSK信号在经过处理后出现了两处非常明显的尖峰。同理，4FSK会出现4处明显的尖峰。如图7（c）所示，正弦调频信号变换后的结果呈现出较宽的峰柱，峰柱上有两处尖峰。考虑正弦调频信号的ZAM-GTFR不难得出结论。观察图1（b），曲线的波峰和波谷拥有较大的能量（能量越高，图中的黑色越深），但数量有限；曲线的其他部分能量较小，但数量可观。在经过能量积累后（类似从横截面对时频图进行投影）就会出现带状的能量峰柱，而波峰波谷能量稍大，表现为带状峰柱上的两尖峰。另外，正弦调频信号模值中的峰柱宽度和调制带宽有关，调制带宽越大，峰柱越宽。当带宽较小时，正弦调频信号与相位编码信号的特征很像，出现一处明显尖峰。

基于上述分析，本文先设定阈值κ，κ取信号ZAM-GTFR在最佳旋转角度的Radon变换的模值均值的2倍，如图7虚线所示。搜索超过κ的尖峰数m，若m大于2判为频率编码信号，m代表频率的个数；若m=2，则搜索两尖峰之间的最小值，计算此最小值与κ的比值α，若α＞0.8将其判为正弦调频信号，令m=1.5，否则判为2FSK信号；若m为1，则提取ZAM-GTFR中的时频脊线，提取脊线时为了提高特征的稳健性要去掉那些能量过小的点，求时频脊线的标准方差σ，若σ＞0.01判为正弦调频信号，令m=1.5，否则判为相位编码信号。

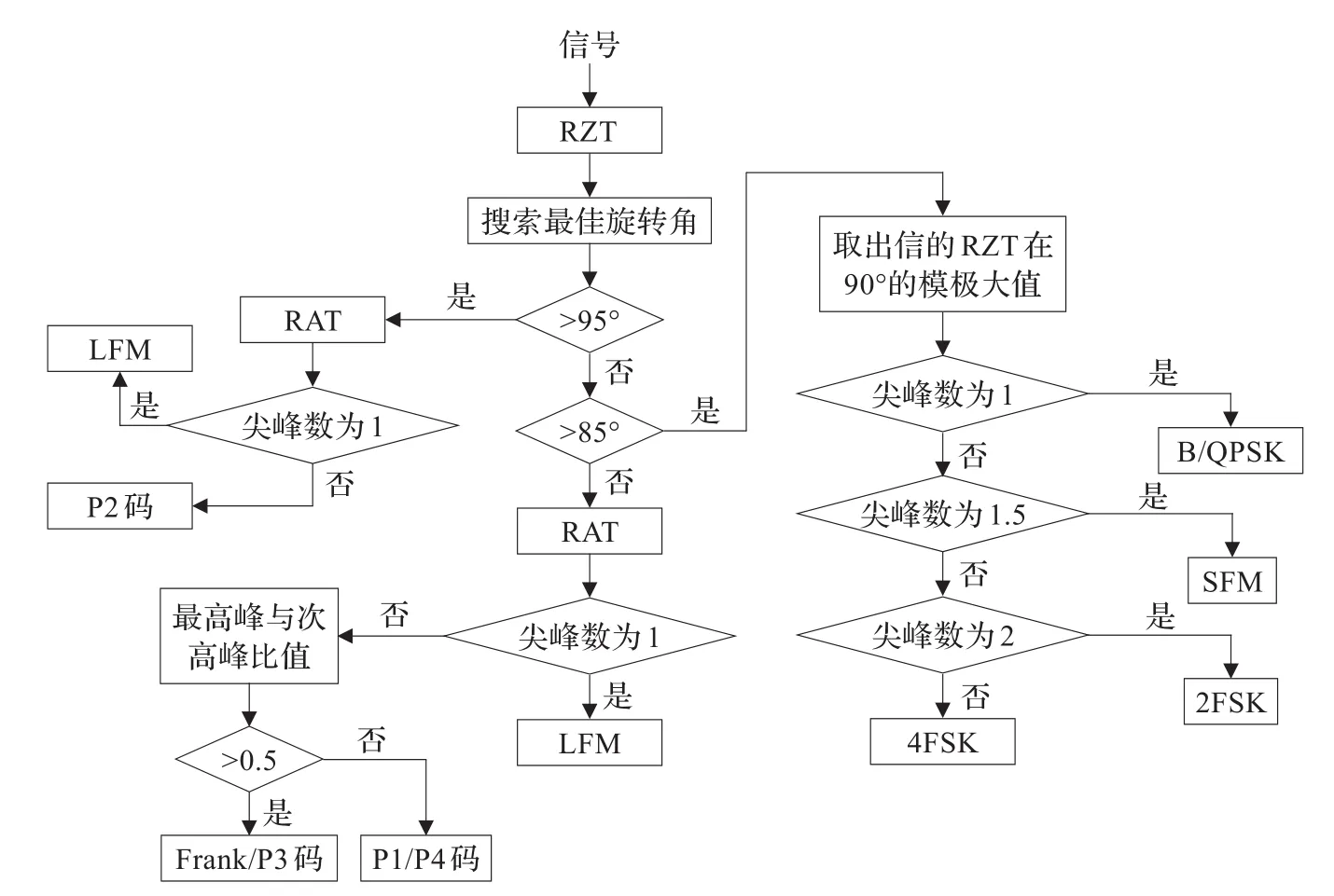
图8 整体识别流程图

5 仿真流程与结果

5.1 识别的流程

依据上述识别原理，本文给出了识别的整体流程图，如图8。

该流程首先对信号进行RZT得到不同旋转角下信号RZT的模极大值，搜索所有模极大值的峰值得到最佳旋转角。判断最佳旋转角是否大于95°，大于95°则计算最佳旋转角下信号的RAT，利用4.2节中的方法判断尖峰数是否为1。若为1则将信号判为LFM信号；否则判为P2码信号。如果最佳旋转角小于95°，判断其是否大于85°。若最佳旋转角大于85°，提取在90°旋转角下信号RZT的模值，利用4.3节中的方法计算尖峰数。若尖峰数为1，将信号判定为B/QPSK信号；若尖峰数为1.5，将信号判为SFM信号；若尖峰数为2，将信号判为2FSK信号，否则将其判为4FSK信号。如果最佳旋转角小于85°，计算最佳旋转角下信号的RAT，利用4.2节中的方法判断尖峰数是否为1。若为1，将信号判为LFM信号；否则计算最佳旋转角下信号RAT模值中的最高峰与次高峰的比值。若该比值大于0.5，判为Frank/P3码信号，否则判为P1/P4码信号。

5.2 仿真验证

根据图8中的识别流程，本文利用Matlab软件对该算法进行仿真。参与仿真的信号为频率调制信号（包括LFM信号、正弦调频信号、2FSK信号和4FSK信号）和相位编码信号（包括BPSK、QPSK、Frank码和P1～P4码信号）。信号载频取50 MHz，采样频率为200 MHz，采样点数为512点。本文选取的正弦调频信号宽带调频信号带宽为10 MHz，窄带调频信号带宽为3 MHz；BPSK和QPSK信号的相位编码随机产生；频率编码信号的频率编码在25～75 MHz间随机产生；多相编码信号的码长取64。噪声是均值为0，方差为1的高斯白噪声；信噪比取-5～5 dB，对每类信号每隔1 dB作300次的蒙特卡罗仿真实验。

图9给出了不同信噪比下各类信号的正确识别率。

图9 不同信噪比下信号分类性能

由图9中的总识别曲线可知，本文的算法具有良好的抗噪性，在-3 dB时信号的平均正确识别率均能达到将近94%。另外，就不同种类信号而言，本文方法对Frank/P3码信号的识别正确率最高，对相位编码（BPSK和QPSK）以及正弦调频信号的识别正确率最低。对Frank/P3码信号识别率高的原因在于，首先利用RZT按斜率将其分为两大类，该方法非常稳健，在非常低的信噪比下仍能区分两大类信号；而后的RAT变换也有很好的抗噪性，且变换后的Frank码和P3码信号有两条幅度近似的尖峰极易与LFM信号区分开。而P1码、P2码和P4码信号在低信噪比时的识别率之所以低于Frank/P3码信号，是因为其次高峰值的能量较最高峰低得多，导致在强噪声干扰下被误判为LFM信号。就正弦调频信号和B/QPSK信号而言，宽带的正弦调频信号的识别率是比较高的，但窄带的正弦调频信号的时频脊线在低信噪比下与相位编码信号的极难分辨，从而拉低了该类信号的识别率。另外，大量仿真实验表明，当频率编码信号不同频率成分所占比例较均衡时识别率非常高，比例严重失衡时识别率很低。这是由于当某种频率成分所占比例很低时，经过RZT后，其最佳旋转角对应的RZT模值的幅度也会很小，极有可能淹没在噪声中，从而导致被误判。

6 结束语

提出了一种可以识别二/四相编码信号、多相编码信号、频率编码、正弦调频信号和线性调频信号等多种具有复杂调制形式的脉压雷达信号的识别方法。本文方法利用既能处理线性调频类信号又能处理非线性调频类信号的ZAM-GTFR提取信号的时频特征，在此基础上利用Radon变换提取最佳旋转角将信号分为零斜率信号和非零斜率信号两大类。接着，经过一定的变换提取满足条件的信号尖峰数，对剩下的信号进行分类。该方法提取的特征明显，能同时满足人工辅助分类和自动分类的要求；具有良好的抗噪性，信号的平均正确识别率能在-3 dB时达到94%。然而，本文方法无法将多相编码信号中的Frank/P3码信号和P1/P4码信号分开，对BPSK信号和QPSK信号也未进行细分，下一步将继续解决这些问题。

总之，本文为复杂调制的脉压雷达信号的分类提供了一种可行的方案，相信随着硬件技术的发展，不久的将来本文的方法能应用到电子对抗雷达侦察装备中。

[1]袁伟明，王敏，吴顺君.低截获概率雷达信号的调制识别研究[J].信号处理，2006，22（2）：153-156.

[2]李明晏，张鲁筠，江铭炎，等.复杂脉内调制雷达信号的识别方法[J].计算机工程与应用，2011，47（15）：156-164.

[3]周欣，吴瑛.核Fisher判别分析在数字信号分类中的应用[J].北京邮电大学学报，2011，34（1）：35-39.

[4]周欣，吴瑛，杨宾，等.一种基于频带能量算子的FSK信号分类新方法[J].信号处理，2010，26（6）：843-847.

[5]林茂庸，柯有安.雷达信号理论[M].北京：国防工业出版社，1984：128-178.

[6]Skolnik M L.雷达手册[M].周万幸，译.3版.北京：电子工业出版社，2010：309-343.

[7]Choi H I，Williams W J.Improved TF representation of multicomponent signals using exponential kenerls[J].IEEE Trans on Acoust，Speech，Signal Processing，1989，37（6）：862-871.

[8]Zahir M，Boashash B.Adaptive instantaneous frequency estimation of multicomponent FM signals using quadratic time-frequency distribution[J].IEEE Trans on Signal Processing，2002，50（8）：1866-1876.

[9]Zeng D，Zeng X.Automatic modulation classification of radar signals using the Generalized Time-Frequency Representation of Zhao，Atlas and Marks[J].IET Radar Sonar Navig，2011，5（4）：507-516.

[10]张贤达，保铮.非平稳信号分析与处理[M].北京：国防工业出版社，1998：1-180.

[11]徐海源，黄知涛，周一宇.基于Radon变换的具有线性调频特性的多相码编码信号参数估计[J].信号处理，2008，24（2）：172-176.

LI Jian,ZHANG Guoyi,WANG Changyu

Department of Aviation Information Countermeasure,Aviation University of Air Force,Changchun 130022,China

With the wide application of complex modulated compression radar signal,traditional identification method can’t satisfy the need of modern electronical reconnaissance.Aiming at this problem,an identification method based on the Generalized Time-Frequency Representation of Zhao,Atlas and Marks（ZAM-GTFR）and Radon transform is put forward.After carry out ZAM-GTFR and Radon transform on signal,this method makes use of the optimal rotational angle and number of summits to identify signal.This method can identify many kinds of complex modulated compression radar signals,including sinusoid frequency modulated signal and poly-phase modulated signal.Simulation results verify that correct identification ratio of this method can reach 94%when signal-to-noise ration is-3 dB.

Generalized Time-Frequency Representation of Zhao，Atlas and Marks（ZAM-GTFR）;Radon transform;complex modulation;radar signal identification

如今，脉压雷达采用的脉内调制形式日益增多且越来越复杂。而传统的识别方法只能识别有限的几种简单调制样式的雷达信号。为了解决这个问题，提出一种基于ZAM-GTFR法和Radon变换的分类方法。该方法通过对信号进行ZAM-GTFR分析以及Radon变换提取最佳旋转角和满足一定条件的尖峰数，将信号区分开，能识别包括正弦调频信号和多相编码信号等在内的多种具有复杂调制形式的脉压雷达信号。仿真实验表明，该方法在-3 dB时能达到94%的平均正确识别率。

ZAM-GTFR方法；Radon变换；复杂调制形式；雷达信号识别

A

TN911.7

10.3778/j.issn.1002-8331.1111-0149

LI Jian,ZHANG Guoyi,WANG Changyu.Identification method for complex modulated compression radar signal.Computer Engineering and Applications,2013,49（13）：198-203.

李建（1988—），男，硕士，主要研究领域为脉冲压缩雷达信号脉内特征分析技术研究；张国毅（1965—），男，博士，教授；王长宇（1975—），男，博士，讲师。E-mail：284182641@qq.com

2011-11-14

2012-01-16

1002-8331（2013）13-0198-06

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1721.067.html