SAR图像统计模型综述

李永晨，刘浏

上海交通大学 自动化系系统控制与信息处理教育部重点实验室，上海 200240

SAR图像统计模型综述

李永晨，刘浏

上海交通大学 自动化系系统控制与信息处理教育部重点实验室，上海 200240

1 引言

合成孔径雷达（SAR）图像统计建模研究是对图像信息从统计学的角度进行分析，它在SAR图像相干斑噪声滤波、图像分割及分类、目标检测与识别等处理中发挥着重要作用[1]。

SAR图像统计分布模型的研究与成像雷达的发展紧密相关。早期的成像雷达采用真实孔径的天线进行成像，由于天线尺寸的限制，图像的分辨率比较低，在获取的雷达复图像实部与虚部分量服从高斯分布的假设下，图像幅度服从瑞利分布，强度服从负指数分布。随着雷达分辨率的提高，瑞利分布的应用受到了一定的限制，尤其是对于高分辨率海杂波，通过实验数据验证，对数正态分布[2]和韦布尔分布[3]能够更好地实现雷达图像统计的描述。雷达技术的发展促进了成像雷达从真实孔径向合成孔径方向发展，SAR的出现开创了雷达成像发展的一个新领域。SAR由于电磁波的相干作用而在获取的图像中出现大量的类似于噪声的相干斑，相干斑构成了SAR图像的基本特征，相干斑模型基础上的SAR图像统计建模研究形成了一类基于先验假设的统计模型。

结合成像雷达的发展，SAR图像统计分布模型可以分为两大类：基于相干斑的先验假设统计模型和基于实验数据的经验分布模型。基于相干斑的先验假设统计模型从相干斑的统计特性出发，建立了相干斑幅度服从瑞利分布和强度服从负指数分布的模型[4-5]，在此基础上多视相干斑强度服从伽马分布，幅度服从Nakagami分布[1]。对于高分辨率SAR图像，图像中不仅存在着相干斑，还表现出大量的纹理特征，在相干斑和纹理信息乘积模型的框架内，形成了多种适于描述均匀与非均匀区域SAR图像的统计分布模型，包括K-分布[1，6-9]、广义逆高斯分布[10]、皮尔逊系统分布[11-12]。在原有相干斑统计假设的基础上，采用广义中心极限定理可以推出SAR图像幅度服从拖尾瑞利分布[13]。在SAR复图像实部与虚部服从广义高斯分布的假设下，可以推出图像幅度服从广义高斯瑞利分布[14]。基于实验数据的经验分布模型是通过对真实SAR图像数据统计建模实验的验证而获得的模型，主要包括对数正态分布[1-2]、韦布尔分布[1，3]、Fisher分布[15]、广义伽马分布[16-17]模型。

2 SAR图像统计模型

2.1 先验假设统计模型

SAR图像的显著特点是图像中存在大量的相干斑噪声，它是由于目标散射电磁波的相干作用而在图像中表现出的颗粒状的噪声模式[1]。Goodman从统计学的角度对激光斑的统计特性进行了深入的研究，建立了斑特性的统计分布模型，这些分布模型对于雷达图像和声纳图像中的斑噪声同样适用[4]。在斑噪声统计分布模型的基础上，形成了一类SAR图像统计分布模型。

2.1.1 瑞利分布

在SAR复图像相干斑噪声实部与虚部分量服从零均值等方差的高斯分布，且相互独立的假设下，SAR图像幅度服从瑞利分布[1，4]：

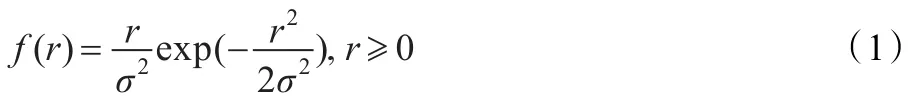
强度服从负指数分布：

其中，σ2为实部与虚部分量高斯分布的方差。

2.1.2 伽马分布

在单视SAR图像强度服从负指数分布的基础上，可以推出多视SAR图像强度服从伽马分布[1]：

幅度服从Nakagami分布，又称为“平方根伽马分布”：

其中，Γ(·)为伽马函数[18]，L为多视视数，μ等于式（1）、（2）中方差σ2的两倍。

2.1.3 K-分布

K-分布是在SAR图像乘积模型框架下发展的一种复合概率分布模型[6-9]。乘积模型将SAR图像表示为纹理分量和相干斑相乘的形式[9]：

其中，τ表示纹理分量，n表示相干斑噪声分量。

假设纹理分量τ和相干斑噪声n均服从于伽马分布，可以推出SAR图像强度统计服从K-分布，其概率密度函数如下[1]：

其中Kv-L为v-L阶第二类修正的贝塞尔函数[18]，v为阶次参数，μ为形状参数，L为视数。

根据强度与幅度的关系，I=r2，可以推出SAR图像幅度统计服从平方根K-分布[19]：

2.1.4 逆高斯分布

乘积模型为SAR图像统计建模提供了一个框架。Frery等在乘积模型的基础上，用广义逆高斯分布对纹理相关的目标后向散射统计进行建模，将其与服从伽马分布的相干斑统计相乘，形成了一类能够描述均匀、不均匀和极不均匀区域SAR图像统计的ς模型[10]。由于ς模型中包含3个未知参数α、γ、λ，参数估计非常困难。为了使ς模型能够应用，Frery等考虑了ς模型的两种特殊情形：

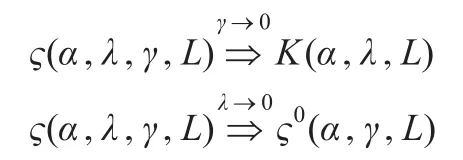
K(α，λ，L)即为K-分布模型，ς0(α，γ，L)为目标后向散射统计服从逆高斯分布时的乘积模型，为了方便这里简称为“逆高斯分布”。SAR图像幅度和强度统计逆高斯分布的概率密度函数如下[10]：

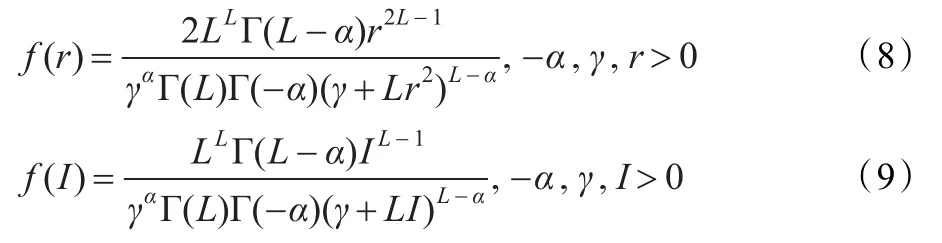
其中，α、γ为模型参数，L为视数。

文献[10]还提到逆高斯分布特别适于对城市、森林等非均匀区域SAR图像的统计建模，通过后面的实验结果，也可以进一步验证逆高斯分布的统计建模能力。

2.1.5 皮尔逊系统分布

皮尔逊系统分布是在SAR图像乘积模型框架内的进一步发展，它通过求解皮尔逊系统的4种分布：第一类Beta分布、伽马分布、逆伽马分布和第二类Beta分布，对纹理相关的目标散射统计进行建模，与服从伽马分布的相干斑统计相乘而形成的统计模型[11-12]。此时，K-分布、逆高斯分布分别对应于皮尔逊系统伽马和逆伽马分布基础上的乘积模型，因此这里只给出第一类Beta分布和第二类Beta分布基础上的SAR图像统计模型，分别称为W-分布和U-分布，二者的概率密度函数如下[11-12]：

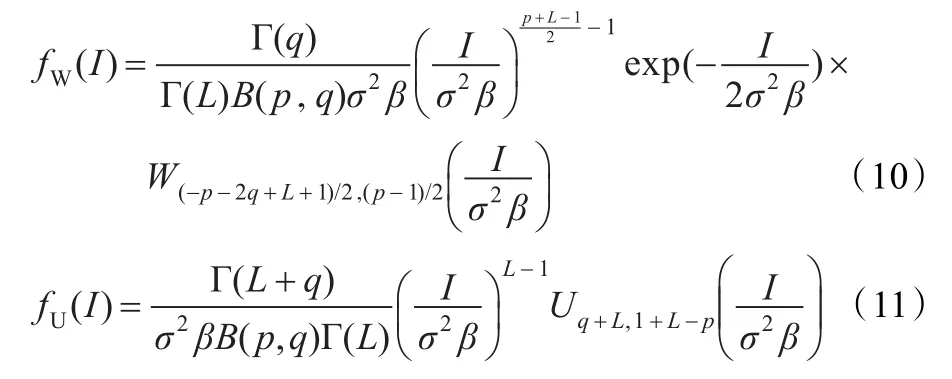
虽然建立了乘积模型框架内的W-分布、U-分布模型，但是二者的模型参数估计都难于实现，从式（10）、（11）也可以直接看出。因此，在实际中很少用到以上两种统计建模方法。

2.1.6 拖尾瑞利分布

在均匀区域SAR图像一个分辨率单元内，当存在大量随机散射子时，应用中心极限定理可以得出SAR复图像实部与虚部分量服高斯分布[5]。在同样的条件下，Kuruoglu等提出对大量同分布的散射子应用广义中心极限定理时，其整体统计特性满足α稳态准则[13]。由此，用α稳态分布对SAR复图像实部和虚部分量进行统计建模，可以推出SAR幅度图像服从拖尾瑞利分布[13]：

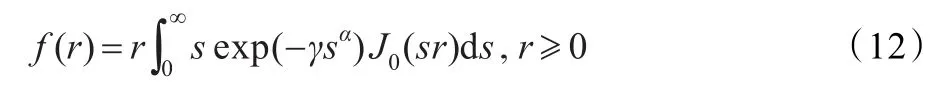
其中，α、γ为大于零的模型参数，J0(·)为零阶第一类修正的贝塞尔函数[18]。该概率密度函数无法求出严格的解析式，概率密度值只能采用数字积分法进行求解。实验表明数字积分区间选取的大小对概率密度函数有严重的影响，有时甚至出现概率密度函数严重振荡的情况，因此这些因素导致拖尾瑞利分布在应用中受到了一定的限制。

2.1.7 广义高斯瑞利分布

Moser等提出对SAR复图像实部与虚部分量采用广义高斯分布进行建模，可以推出了SAR图像幅度统计服从广义高斯瑞利分布[14]：

其中，θ为复图像相位，γ为尺度参数，c为形状参数，且有γ，c＞0。与拖尾瑞利分布相似，该概率密度函数也求不出严格的解析式，均值和方差不易求解，积分项只能采用数字积分法进行求解。

2.2 经验分布模型

2.2.1 对数正态分布

在高分辨率观测下，瑞利分布不再适于描述目标雷达散射截面积起伏引起的目标杂波统计特性的变化。通过实验数据表明，对数正态分布可以实现高分辨条件下场景杂波统计的幅度描述[2]。同样，对于SAR图像统计，对数正态分布也表现出较好的统计建模能力。

对数正态分布的概率密度函数如下：

其中，μ和σ是lnr的均值和标准差。

对于强度图像，根据强度与幅度的变换关系，当幅度服从对数正态分布时，可以推出强度也服从对数正态分布。因此，对数正态分布不仅可以对幅度图像进行建模，还可以对强度图像进行建模。

对数正态分布可以实现对高分辨率海杂波和陆地非均匀区域（如城市区域）SAR图像的统计建模，特别是图像中存在着剧烈变化的区域，可以获得较好的统计建模精度[1]。

2.2.2 韦布尔分布

韦布尔分布最早应用于对海杂波的统计描述。在高分辨率条件下，雷达海面观测数据不再服从瑞利分布，根据实验数据验证，韦布尔分布可以获得对杂波幅度较好的统计拟合效果[3]。

韦布尔分布的概率密度函数如下[1]：

其中，b为尺度参数，c为形状参数。

对于韦布尔分布，当c=2时，概率密度函数与瑞利分布相同；当c=1概率密度函数与负指数分布相同。因此，韦布尔分布可以对单视SAR图像强度和幅度统计进行建模，但是对于多视SAR图像，韦布尔分布的建模精度会显著下降。

2.2.3 Fisher分布

对于高分辨率城市区域的SAR图像，由于成像区域不是均匀变化的，传统的统计分布模型不再适用于图像的统计描述。在不考虑SAR成像机理的条件下，基于图像强度数据经验分布的Fisher分布可以获得较高的图像建模精度[15]。

Fisher分布的概率密度函数如下：

其中，L图像视数，M＞0，μ＞0。

虽然Fisher分布只是从数学得出的概率分布模型，但它与逆高斯分布具有相似的概率密度函数形式。由于逆高斯分布对非均匀区域具有较好的建模能力，这从另一个方面解释了Fisher分布适合于非均匀SAR图像统计建模的原因。

2.2.4 广义伽马分布

在伽马分布的基础上，文献[16-17]提出SAR图像统计的广义伽马分布模型，通过实验数据表明广义伽马分布能够更好地实现SAR图像的统计建模。

广义伽马分布的概率密度函数如下[16]：

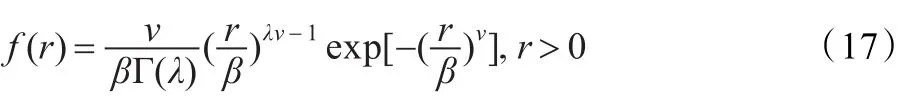
其中，β为尺度参数，λ为形状参数，v为能量参数。

广义伽马分布有3个分布参数，文献[16]中还进一步证明了在分布参数选取为一些特定值时，瑞利分布(v=2，λ=1)、指数分布(v=1，λ=1)、对数正态分布(v=1，λ→0，or，∞)、韦布尔分布(λ=1)）和伽马分布(v=1)都是广义伽马分布的特例，因此运用广义伽马分布对SAR图像统计建模更具有一般性。

3 模型参数估计

参数估计是统计学研究中一类重要的问题，它是在模型参数未知的情况下，由观测数据实现对未知参数的估计。对于概率分布模型，经典的参数估计方法有矩估计（Method of Moments，MoM）和最大似然估计（Maximum Likelihood，ML）[19-20]，但是MoM和ML对于一些复杂的分布模型无法实现参数估计。2002年Nicolas等在概率密度函数梅林变换的基础上，提出了一种参数估计的新方法——对数累量法（Method of Logarithmic Cumulants，MoLC）[21]。Krylov等对MoLC参数估计的一致性和实现步骤进行了详细的介绍，而且还证明了与MoM相比，MoLC具有更高的参数估计精度[22]。MoLC已经在概率分布模型的参数估计中得到应用[14-15，17]。下面对MoLC和SAR图像统计模型参数MoLC估计的结果进行详细的介绍。

3.1 对数累量法（MoLC）

MoLC是建立在概率密度函数梅林变换的基础之上的。梅林变换是一种积分变换，对于随机变量x∈(0，+∞)的概率密度函数f(x)，其梅林变换有如下形式[22]：

对上式求s=1处的i阶导数，可以得到变量x的对数矩估计：

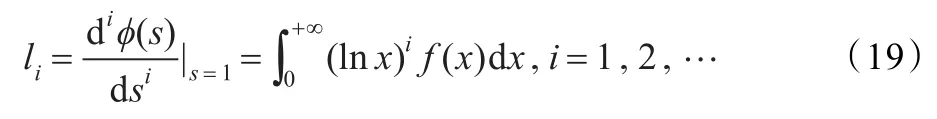
对式（18）取对数并求其在s=1处的i阶导数，可以得到变量x的对数累量：

与传统的矩与累量之间的关系一样[20]，对于低阶的对数矩li和对数累量ki有如下关系：

因此，对于N个观测值xj，对数累量估计为：

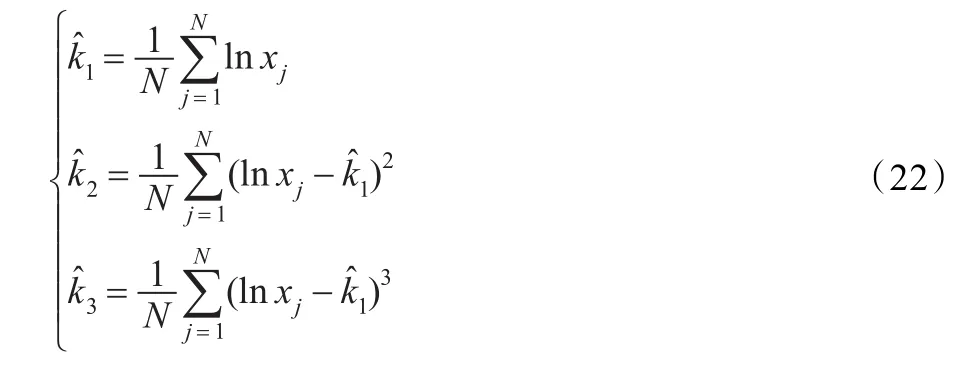
3.2 模型参数MoLC估计

对第2章的SAR图像统计模型，按照上文给出的模型参数估计MoLC，计算相应的对数累量表达式，如表1所示。皮尔逊系统分布和拖尾瑞利分布对数累量不能求出解析的表达式，因此在表1中没有给出。

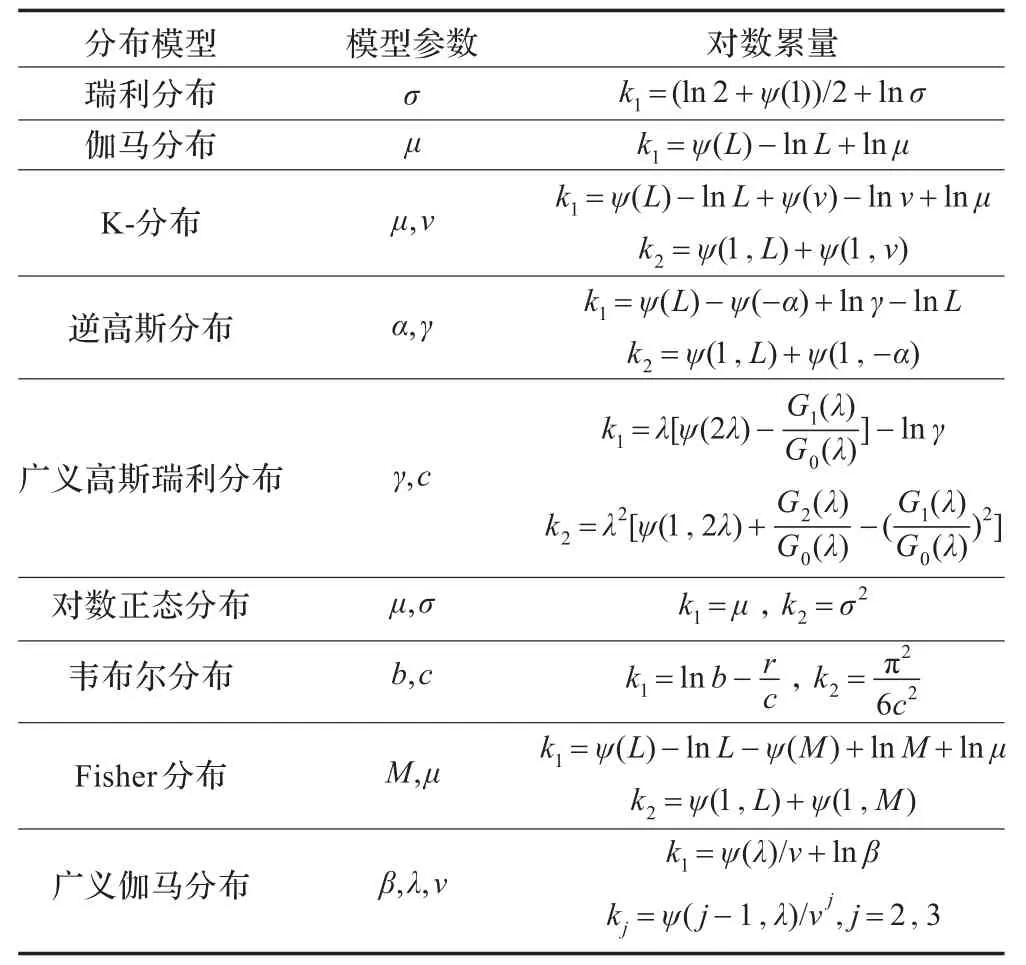
表1 SAR图像统计模型参数估计

表1中，ψ(·)表示digamma函数，ψ(i，·)表示i阶polygamma函数[18]；广义高斯瑞利分布对数累量式中λ=1/c，Gi(i=0，1，2)的定义参考文献[14]。

4 建模精度评估

图像统计建模的精度是区分模型优劣的重要指标，在对概率分布模型建模精度评估中已经出现了很多方法，如基于统计学的皮尔逊χ2检验与K-S距离[19，23]，基于信息熵的K-L距离[20，24]。下面对以上3种图像建模精度的评估准则进行详细的介绍。

4.1 皮尔逊χ2检验

皮尔逊χ2检验是一种基于实验观测数据的近似检验，可以用于检验观测数据和假设分布模型的拟合程度，检验统计统计量如下[19，23]：

其中，K表示n个观测数据划分的统计检验子区间的个数，qi表示假设分布模型在第i个子区间内的概率，ni表示第i个子区间中观测数据的个数。

检验统计量q近似服从于χ2(K-s-1)分布，χ2的自由度不依赖于观测数据的个数，而是取决于K和假设分布模型中未知参数个数s，表示为K-s-1，因此观测数据服从于假设分布的概率可以表示为：

4.2 Kolmogorov-Smirnov（K-S）距离

K-S距离是建立在观测数据基础上的非参数统计检验，通过比较观测数据经验分布与假设分布模型累积概率分布函数之间的偏差作为评价假设分布模型与观测数据之间的拟合精度，当二者的偏差为零时，说明观测数据服从于假设分布模型。

对于n个观测数据xi，设不超过x的样本数目为nx，则x的经验分布函数可以表示为点估计的形式[19]：

令假设分布模型的累积概率密度函数为F(x)，则K-S检验统计量表示为[19，23]：

q表示F(x)和F0(x)和之间的最大偏差，从几何角度来看它表征了两个分布之间的距离，因此统计量q可以直接作为一个距离指标来表示观测数据与假设分布模型之间的匹配程度。

4.3 Kullback-Leibler（K-L）距离

K-L距离（或信息）表示两个概率分布模型之间差异的信息量，也可以表述为从一个概率分布模型预测另一个概率分布模型的信息损失量。当g(x)表示已知分布模型，f(x)表示假设分布模型，由f(x)预测g(x)时的K-L距离定义如下[20，24-25]：

对于离散的随机变量xi，K-L距离可以表示为以下形式：

其中，g(xi)和f(xi)分别表示在xi处的概率，且满足

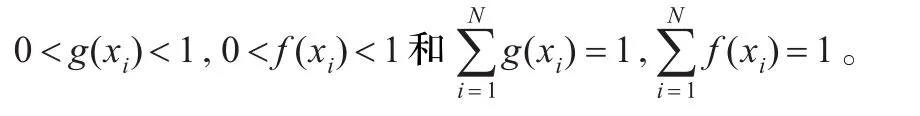
K-L距离具有方向性，从g→f和f→g的K-L距离是不相等的，一般在表示两个概率分布之间的差异度时，采用对称K-L距离的形式[24-25]：

5 实验与分析

前面对SAR图像统计模型、参数估计和建模精度的评估准则进行了介绍，下面结合真实的SAR图像数据进行统计建模实验。

SAR图像数据主要通过机载SAR、星载SAR传感器获得。由于国内的机载SAR数据较少，国外的机载SAR数据一方面是获取比较困难，另一方面是成像的时间较早，不能很好地反映当前SAR成像系统发展的水平，因此这里选取的SAR图像都是国外近几年发射星载SAR系统的成像数据，包括加拿大RadarSat-2（RS2）、德国TerraSAR-X（TSX）和意大利COSMO-Skymed（CSKS）的成像数据，成像时间集中在2007年—2008年之间，成像区域包括海面、海冰、农田、森林、城区、山区和熔岩7种地表类型。如图1所示。图像大小均为400像素×400像素。

图1给出了低分辨率和高分辨率7种地表类型SAR图像数据（图1（c）海冰和图1（l）熔岩除外），图像类型均为幅度图像。对以上图像采用第2章给出的统计分布模型进行建模实验，模型参数采用第3章介绍的MoLC进行估计，并运用第4章中介绍的皮尔逊χ2检验、K-S距离和K-L距离3种评估准则进行建模精度评估，实验结果如表2、3、4所示（表3中结果都是放大10倍后的数值，因此真实的K-S距离需要乘以10-1）。

实验有三点需要说明：一是在实验中没有采用拖尾瑞利分布和皮尔逊系统分布，由于拖尾瑞利分布概率密度函数没有解析式，应用数字积分进行计算时结果不唯一，皮尔逊系统分布族中K-分布、B-分布分别与经典K-分布与逆高斯分布相同，而W-分布、U-分布参数估计不易实现；二是在文献[15]中Fisher分布用于强度图像的统计建模，但是Fisher分布是一种经验分布模型，与图像类型是不相关的，因此也可以对幅度图像进行统计建模，通过实验表明其对幅度图像建模也能取得很高的建模精度；三是广义高斯瑞利分布在图像统计建模时存在着局限性，当SAR图像统计的二阶累量小于0.296时，广义高斯瑞利分布无法应用[14]。

图1 SAR图像数据

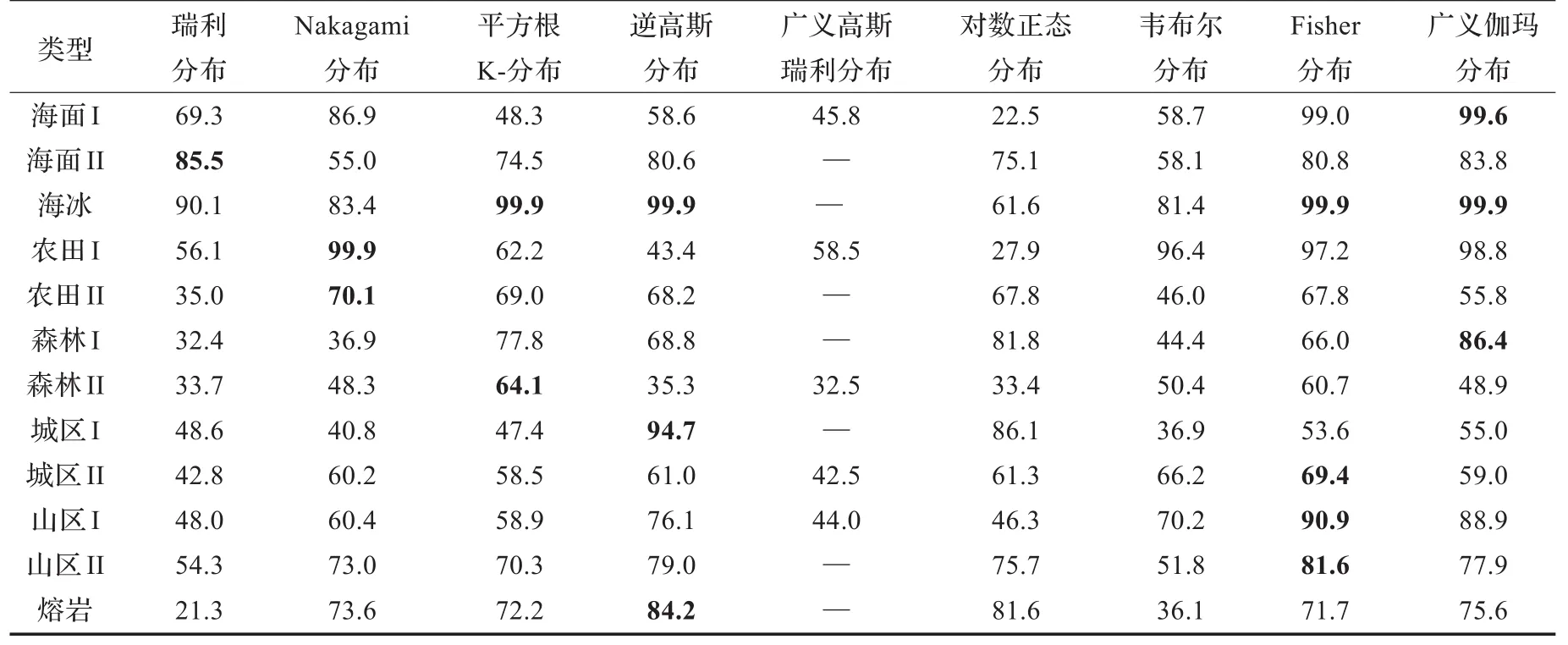
表2 统计建模精度皮尔逊χ2检验（%）

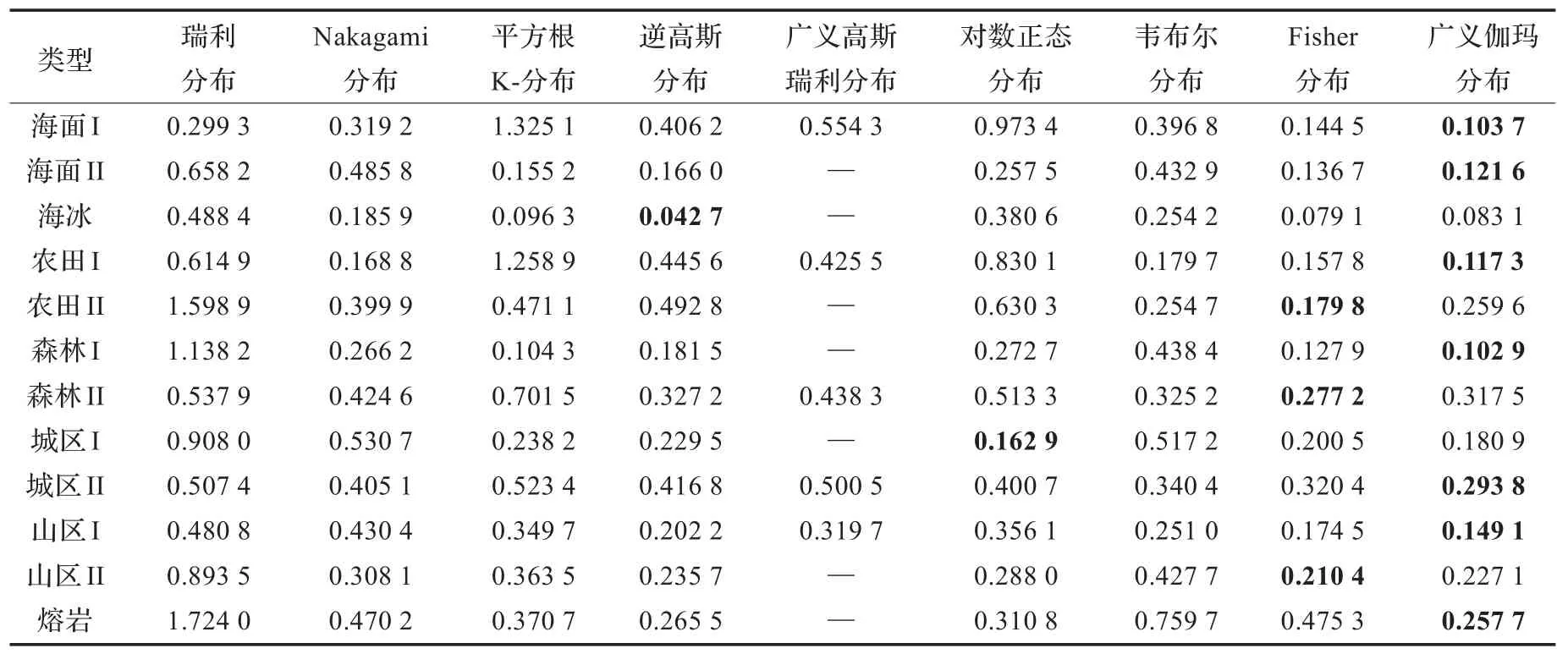
表3 统计建模精度K-S距离

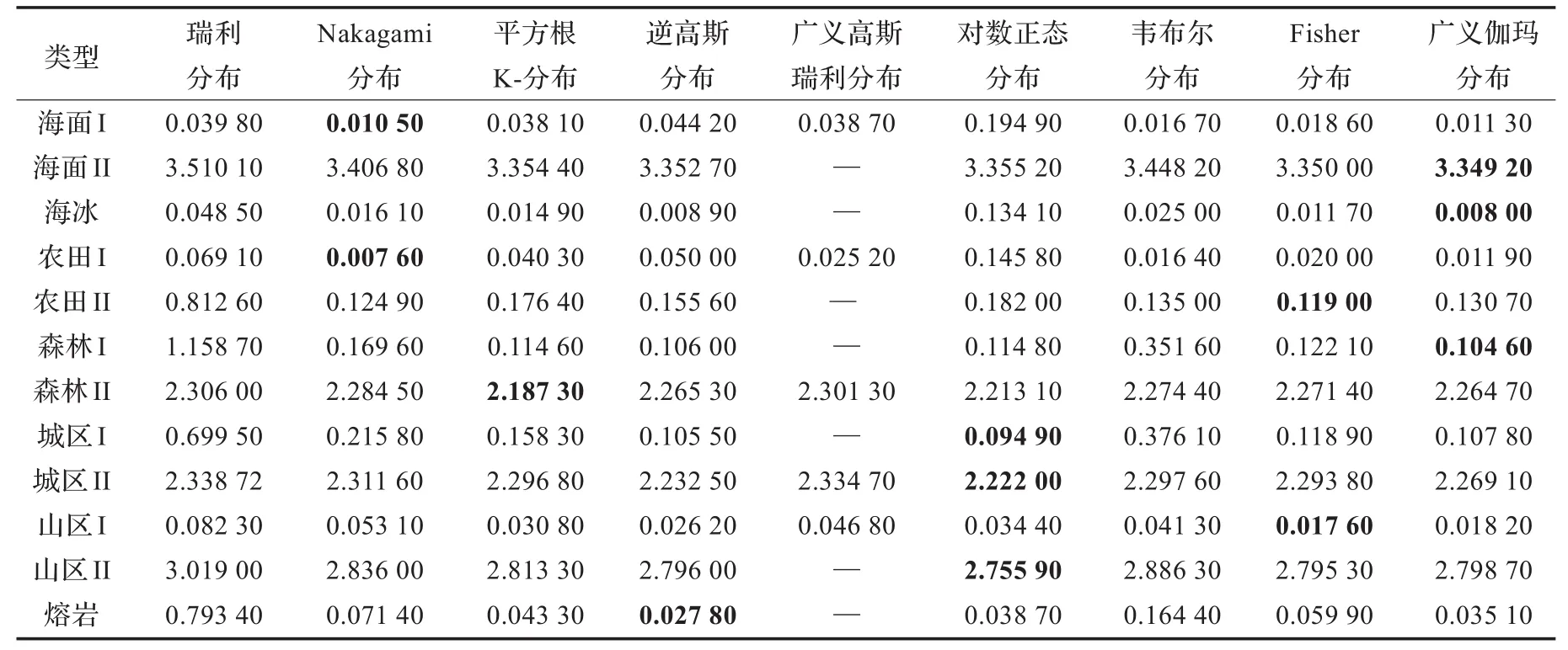
表4 统计建模精度K-L距离

由于各个SAR的差异性，如成像模式、工作频段、入射角、多视处理、极化方式等，不同的SAR传感器获取的图像即使对同一种地表类型也存在很大的差异，因此对统计模型建模精度评估的结果有很大的影响，如表2、3、4，同一种地表类型SAR图像最优的统计模型也不相同。对于这种问题有两种可能的解决办法：一是采用同一个SAR对所有地表类型进行成像，但是实验数据获取的成本比较大，而且该成像数据统计建模的结果是否具有一般性也是一个值得研究的问题；二是进行SAR图像仿真，可以低成本大量地获取不同地表类型的SAR图像，然而现在SAR图像仿真技术还不是很成熟，有效的SAR图像仿真数据还没有获得。

皮尔逊χ2检验、K-S距离和K-L距离3种评估准则是对SAR图像统计模型从不同方面建模精度的评估，因此即使对于同一幅SAR图像，采用不同的评估准则进行统计模型评估时，最优的统计模型可能也不相同。如对于图1（a）海杂波SAR图像，建模精度结果对应于表2、3、4的第1行，采用皮尔逊χ2检验和K-S距离进行评估时，最优的统计模型是广义伽马分布，而采用K-L距离进行评估时，最优的统计模型是Nakagami分布。

对于表2、3、4中的实验结果，可以分别从统计模型和SAR图像地表类型两个方面进行分析。从统计模型的角度进行分析，在3种建模精度评估准则下，计算每个统计模型适宜的地表类型个数。对于图1中不同分辨率下的7种地表类型，分别对照表2、3、4实验结果的每一行寻找3种最优的统计模型，如表2中第1行中最优的3种统计模型为Nakagami分布、Fisher分布和广义伽马分布；然后分别按照皮尔逊χ2检验、K-S距离和K-L距离评估准则统计每个统计模型适宜的地表类型个数，从而可以得出每一种统计分布模型适宜的地表类型总数，如图2所示。

从图2中可以直观看出，在3种建模精度评估准则下，逆高斯分布、Fisher分布和广义伽马分布适宜的SAR图像地表类型个数均在3个或3个以上，尤其是广义伽马分布，与其他分布模型相比，该模型表现最好的建模能力，这也可以理解的，是由于广义伽马分布有3个模型参数。虽然K-分布作为一种重要的SAR图像统计模型，但是对于SAR幅度图像而言，平方根K-分布的建模精度没有达到期望效果。从图2还可以看出，瑞利分布、Nakagami分布、对数正态分布和韦布尔分布只能对一种或几种SAR图像地表类型表现出较好的建模效果。

从SAR图像地表类型的角度进行分析，统计每一种地表类型的3种最优的统计模型。由于对同一幅SAR图像，采用不同的建模精度评估准则时，最优的统计模型分布不相同，因此综合考虑表2、3、4中3种建模精度评估的结果，可以选出图1每一幅SAR图像最优的3种统计分布模型，如表5（表中横轴第2行为概率分布的英语缩写表示，见图2标题部分）。

图2 分布模型适宜的SAR图像地表类型数目

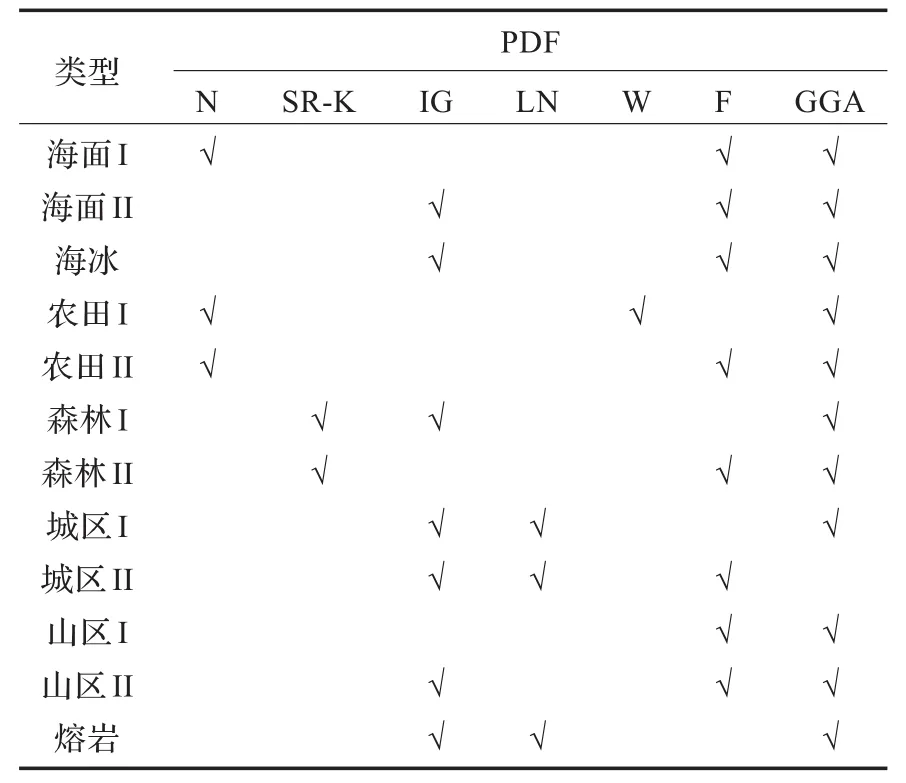
表5 SAR图像地表类型3种最优统计模型

从表5中“√”的分布再次验证了图2显示的逆高斯分布、Fisher分布和广义伽马分布具有更出色的SAR图像建模能力。从表5中还可以得出以下结论：Nakagami分布适于农田区域的图像统计建模，平方根K-分布适于森林区域，逆高斯分布适于海冰、森林、城区、山区等非均匀区域，对数正态分布适于城区，Fisher分布和广义伽马分布适于统计建模的区域最广泛，包括海面、农田、森林、城市、山区等。对于不同的类型的地表区域，最优的统计分布模型不一样，但从整体的统计建模的效果来看，基于先验假设的逆高斯分布和基于实验数据的Fisher分布与广义伽马分布具有更广泛的SAR图像建模适用性。

6 结论

本文对SAR图像统计分布模型进行了总结回顾，按照统计模型的起源分为先验假设统计模型和经验分布模型两大类，共11种统计分布模型；根据参数估计的MoLC实现了模型的参数估计，并给出了模型建模精度评估的皮尔逊χ2检验、K-S距离和K-L距离3种评估准则；最后对真实的SAR图像数据进行建模实验，评估了每一种模型的建模精度。通过对实验结果的分析，不仅得出了适于不同地表类型的SAR图像统计模型，还得出逆高斯分布、Fisher分布和广义伽马分布具有更广泛的SAR图像统计建模能力。

[1]Oliver C，Quegan S.Understanding synthetic aperture radar images[M].[S.l.]：Sci Tech Publishing，2004.

[2]Trunk G，George S.Detection of targets in non-Gaussian sea clutter[J].Aerospace and Electronic Systems，1970（5）：620-628.

[3]Schleher D.Radar detection in Weibull clutter[J].IEEE Transactions on Aerospace and Electronic Systems，1976（6）：736-743.

[4]Goodman J.Statistical properties of laser speckle patterns[M]// Laser Speckle and Related Phenomena.Berlin：Springer-Verlag，1975：9-75.

[5]Goodman J W.Some fundamental properties of speckle[J].J Opt Soc Am，1976，66（11）：1145-1150.

[6]Jakeman E，Pusey P.A model for non-Rayleigh sea echo[J]. IEEE Transactions on Antennas and Propagation，1976，24（6）：806-814.

[7]Jen J.Amplitude distribution of composite terrain radar clutter andtheK-distribution[J].IEEETransactionsonAntennas and Propagation，1984，32（10）：1049-1062.

[8]Oliver C J.A model for non-rayleigh scattering statistics[J]. Optica Acta：International Journal of Optics，1984，31（6）：701-722.

[9]Chitroub S，Houacine A，Sansal B.Statistical characterisation and modelling of SAR images[J].Signal Processing，2002，82（1）：69-92.

[10]Frery A C，Muller H J，Yanasse C C F，et al.A model for extremelyheterogeneousclutter[J].IEEETransactionson Geoscience and Remote Sensing，1997，35（3）：648-659.

[11]Delignon Y，Garello R，Hillion A.Statistical modelling of ocean SAR images[J].IEEE Proceedings of Radar，Sonar and Navigation，1997，144（6）：348-354.

[12]Delignon Y，Pieczynski W.Modeling non-Rayleigh speckle distribution in SAR images[J].IEEE Transactions on Geoscience and Remote Sensing，2002，40（6）：1430-1435.

[13]Kuruoglu E E，Zerubia J.Modeling SAR images with a generalization of the Rayleigh distribution[J].IEEE Transactions on Image Processing，2004，13（4）：527-533.

[14]Moser G，Zerubia J，Serpico S B.SAR amplitude probability density function estimation based on a generalized Gaussian model[J].IEEE Transactions on Image Processing，2006，15（6）：1429-1442.

[15]Tison C，Nicolas J M，Tupin F，et al.A new statistical model for Markovian classification of urban areas in high-resolution SAR images[J].IEEE Transactions on Geoscience and Remote Sensing，2004，42（10）：2046-2057.

[16]Anastassopoulos V，Lampropoulos G A，Drosopoulos A，et al. High resolution radar clutter statistics[J].IEEE Transactions on Aerospace and Electronic Systems，1999，35（1）：43-60.

[17]Li H C，Hong W，Wu Y R，et al.On the empirical-statistical modeling of SAR images with generalized gamma distribution[J].IEEE Journal of Selected Topics in Signal Processing，2011，5（3）：386-397.

[18]Olver F W J，Lozier D W，Boisvert R F，et al.NIST handbook ofmathematicalfunctions[M].[S.l.]：CambridgeUniversity Press，2010.

[19]Papoulis A，Pillai S U.概率，随机变量与随机过程[M].保铮，译.西安：西安交通大学出版社，2004.

[20]Ord J K，Arnold S F，O’Hagan A，et al.Kendall’s advanced theory of statistics[M].[S.l.]：Hodder Arnold，1999.

[21]Nicolas J M.Introduction to second kind statistics：application of Log-moments and Log-cumulants to SAR image law analysis[J].Traitement du Signal，2002，19（3）：139-168.

[22]Krylov V，Moser G，Serpico S B，et al.On the method of logarithmic cumulants for parametric probability density function estimation[R].2011.

[23]DeVore M D，O’Sullivan J A.Quantitative statistical assessment of conditional models for synthetic aperture radar[J].IEEE Transactions on Image Processing，2004，13（2）：113-125.

[24]Burnham K P，Anderson D R.Model selection and multi-model inference：a practical information-theoretic approach[M].New York：Springer，2002.

[25]朱雪龙.应用信息论基础[M].北京：清华大学出版社，2001.

LI Yongchen,LIU Liu

Key Laboratory of System Control and Information Processing of Ministry of Education,Department of Automation,Shanghai Jiaotong University,Shanghai 200240,China

This paper reviews probability distribution models in the study of statistical modeling of Synthetic Aperture Radar（SAR）imagery.According to the origin of each model,all models can be divided into two categories：the statistical models of prior assumptions and the empirical distribution models.The Method of Logarithmic Cumulants（MoLC）which is a new method for parameter estimation is introduced；furthermore,the estimated expressions of logarithmic cumulants of statistical models are computed based on the MoLC.Theevaluation criterions of modeling precision are developed and then implemented in the experiment of modeling real SAR images.Finally,the suitable terrain of SAR imagery for each statistical model is concluded from experimental results.

Synthetic Aperture Radar（SAR）imagery;probability distribution model;parameter estimation;precision evaluation

综述了合成孔径雷达（SAR）图像统计建模研究中的概率分布模型，按照模型起源将所有模型分为了先验假设统计模型和经验分布模型两大类。介绍了一种模型参数估计的新方法——对数累量法，并根据对数累量法计算了统计模型参数估计的对数累量表达式；发展了统计模型建模精度的评估准则，并应用到了SAR图像数据统计建模实验中。通过实验结果得出了每一种统计模型适宜建模的SAR图像地表类型。

SAR图像；概率分布模型；参数估计；精度评估

A

TN957.51

10.3778/j.issn.1002-8331.1301-0356

LI Yongchen,LIU Liu.Review of statistical models of SAR image.Computer Engineering and Applications,2013,49（13）：180-186.

李永晨（1986—），男，硕士研究生，研究领域为SAR与极化SAR图像处理；刘浏（1980—），男，博士，研究领域为图像处理与机器学习。E-mail：yclkj2010@163.com

2013-01-30

2013-03-26

1002-8331（2013）13-0180-07