基于最小生成树的图像分割

黎莹，戴芳，郝勇，左涛

西安理工大学 理学院应用数学系，西安 710054

基于最小生成树的图像分割

黎莹，戴芳，郝勇，左涛

西安理工大学 理学院应用数学系，西安 710054

1 引言

图像分割是利用图像某些特性，如灰度、颜色、纹理等，将图像分割成若干个独立且有意义的连续区域或对象[1]。在每个区域内有相同的特性，这些区域能够表达设计的场景或者物体，符合现实中人眼的视觉特性。按照实现原理的不同，图像分割算法可分为以下四大类：基于阈值的分割方法、基于边缘检测的分割方法、基于区域提取的分割方法和结合特定理论的分割方法。随着各学科新理论和新方法的提出，出现了许多与特定理论相结合的图像分割方法，如基于聚类分析的图像分割方法、基于模糊集理论的分割方法、基于小波变换的分割方法、基于神经网络的分割方法和基于图论的分割方法等。

图论中，将图像的像素映射为图的顶点，顶点和顶点之间的连接映射为边，边的权值代表顶点之间的相似性或差异性，通常构造图的邻接矩阵来实现图像分割。经典的利用图理论进行图像分割的方法有Normalized-Cut（N-Cut）方法[2]、最小生成树方法[3]、最大流最小割方法[4]等。N-Cut方法考虑了所分子区域内的自相似性，利用区域的全局特征，采用“归一化”的方法使算法的分割效果得到改善，然而，归一化分割方法是一个NP完全问题，计算复杂度过高。最大流最小割方法将图像映射为一个网络，对待分割的物体内部（目标）及其外部（背景）像素分别做出不同的标记，给予不同的权重，利用能量最小化的原理进行分割，获得物体的轮廓。该框架具有快速性好，全部最优及抗噪性强的优点，但其必须人工指定目标内部及其外部的像素作为种子点才能进行分割，限制了算法在图像分割中的应用。最小生成树方法进行图像分割时，对图像信息可从全局进行把握，最小生成树的生长过程可以保留低变化区域内部的细节，并且寻找最小权值的过程具有自适应性，从而表现图像的全局特征，符合人眼的视觉特性[5]，保证了算法能够获得比较好的全局分割结果，并且分割效率高，算法数据结构简单。但是当图像的尺寸增加时，构造最小生成树对边进行排序将增加运算负担。另外，利用最小生成树进行全局阈值分割易受到图像噪声以及不同区域间边界的影响，因此利用最小生成树进行图像分割，邻接矩阵的构造和阈值的选取是该方法的关键。文献[6]在阈值的选取上对最小生成树方法进行改进；文献[7]将最小生成树算法和Mumford-Shah理论结合，提出新的优化方案，得到了好的分割效果。

文献[8]提出了一种新的类似最小生成树的方法，减少了构建最小生成树的过程，但是利用类似的最小生成树方法进行分割会得到很多过分割的块。本文基于文献[8]构造了新的分割方法，保留了图像的全局信息，并提出了利用Nearest Neighbor Graph（NNG）对初分割的结果进行合并。该方法较好地保留了图像特征信息，对初分割后的结果进一步的处理，使分割的效果得到改善。

2 结合改进的最小生成树和NNG方法的图像分割

2.1 利用改进的最小生成树进行图像初分割

给定一个无向图G=(V，E)，这里V代表像素集，E代表像素之间的连接称为边，E的大小代表两个相邻像素的差异称为权，若找到连接所有像素的非连通的子集，连接像素的权值和最小则称为最小生成树。利用最小生成树进行图像分割，则是通过割断最小树边的权值大于阈值的边。

图像利用最小树分割，首先要将图像映射到图空间，构造区域邻接图（Region Adjacency Graph，RAG）；对于m×n大小的图像，若构造邻接矩阵将产生(m×n)2大小的矩阵，对于尺寸较大的图像，直接构造RAG耗费大量时间。因此本文改进了最小生成树的构造过程，节约了分割时间。

图1为最小生成树进行图像分割的原理示意图，其中图（a）为人工合成图像，图（b）为将图像（a）映射为图后得到的最小生成树，（c）为割断最小生成树大于阈值的边（阈值设置为1），得到的最后分割图。

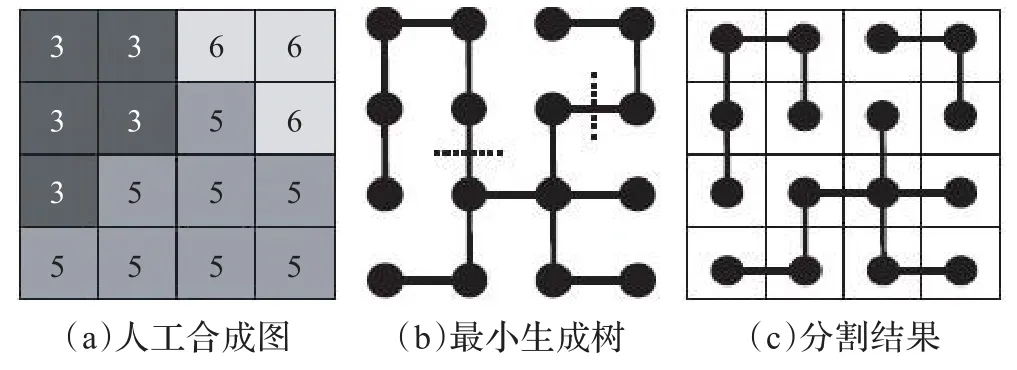
图1 最小生成树分割过程示意图

对于大小为m×n的图像I，本文重新构造一个(2m-1)×(2n-1)大小的矩阵M来存储图的顶点和边，在M中位置(2i-1，2j-1)存储顶点V(i，j)，位置(2i-1，2j)存储顶点V(i，j)与V(i+1，j)的边，位置(2i，2j-1)存储顶点V(i，j)与V(i，j-1)的边，位置(2i，2j)存储顶点V(i，j)与V(i+1，j+1)的边和V(i，j+1)与V(i+1，j)的边中的最小值，在文中令阈值等于I的方差。

对于边的构造，取

图2为本文构造的算法进行图像分割的过程示意图，其中图（a）为对图1（a）中的人工合成图构造的M矩阵，这里对于顶点位置设置为1，边的计算由公式（1）得到；在图（b）中大于阈值的边设为0（这里阈值设定为1）；图（c）为对顶点标号，若一个像素周围的8邻域都为1，则这些像素属于同一区域，将一个区域的元素标记为一类。

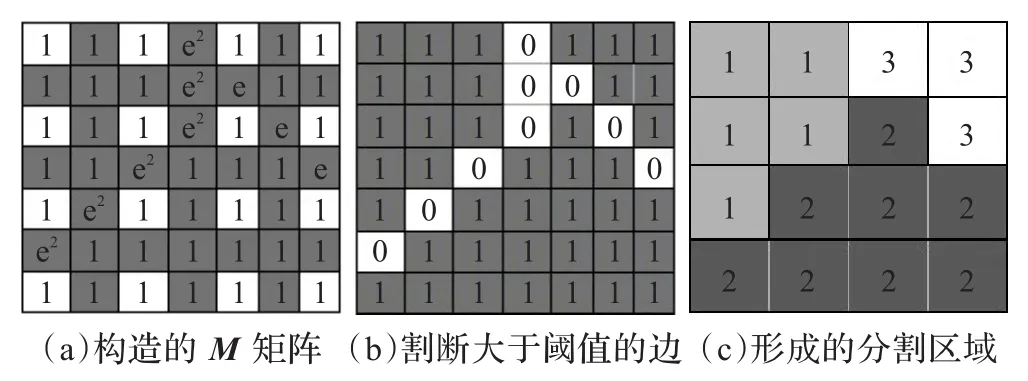
图2 本文构造的算法分割过程示意图

2.2 利用NNG方法对初分割图像进行合并

本文对于利用改进的最小生成树方法得到的初分割结果，设最后得到k个区域，每个区域代表一个顶点，区域的信息用灰度均值代表分别为c(1)，c(2)，…，c(k)，构造RAG，对于新构造的RAG边的定义为：

对于一个RAG和一个无向图G(V，E)，NNG的定义如下：它是一张有向图Gm=(Vm，Em)，其中Vm=V。其边(u，h)的构造如下，u，h∈V，并且如果

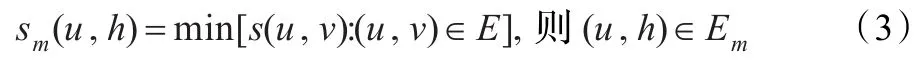
由公式（3）可以得到NNG中的边，按如下方法确定：对于RAG中某个顶点u，设在所有与其相连的边中，只保留具有最小权值的那条边所连接的相邻顶点。因此，在NNG中，顶点u有且仅有一条指向节点v的边，并且当有多于一个顶点使sm（u，v)最小化时，则边指向具有最小标记值的那个顶点。

在构造的相似性矩阵RAG中只保存相似性函数值为1的，其余的值设为∞，利用公式（3）得到最后的NNG。若顶点u和顶点v都保留了s(u，v)这条边，则将u、v这两个区域进行合并，对于合并后的区域更新灰度值以及标号，根据图像的大小设置不同的迭代次数。

3 实验结果

实验1对风景图进行分割，图3（a）为原图，图3（b）为本文方法，图3（c）为文献[8]的方法。

图3 风景图的分割比较

通过实验1，由图3（b）和（c）可以看出本文方法得到了较好的分割效果，从云层和山峰可以看出本文方法得到的分割效果更好。

实验2对Lena图，利用本文和文献[8]方法对分割结果进行比较。图4（a）为原图，图4（b）为本文方法的分割结果，图4（c）为利用文献[8]方法分割并进行NNG合并后的分割结果。

图4 分割效果比较

由实验2的结果可以看出，在图4（c）的面部有过分割的现象，而图4（b）为本文的分割效果，减少了过分割现象的产生。本文方法更好地抓住了全局信息，得到了较好的分割效果。

实验3利用NNG方法进行图像合并，其迭代次数的选取也影响分割的效果，对Lena图选取不同的迭代次数，比较分割后的结果。图5（a）为利用NNG方法进行合并时迭代次数为23的分割效果，图5（b）为利用NNG方法合并时迭代次数为50的分割效果，图5（c）为利用NNG方法合并时迭代次数为100的分割效果。

图5 迭代次数对比图

由图5（a）的结果可以看出，当合并的次数过少时，得到的分割区域很多，有明显的过分割效应。在图5（b）中很多过分割的区域被有效的合并，得到了较好的分割效果，保留了图像的细节信息。但是当合并次数较大时，由图5（c）可以看到其较好地保留了目标区域，但图像的很多细节信息被合并了。

本文的时间复杂度主要包括两部分：（1）利用改进方法构造最小生成树进行分割的时间复杂度为O(m×n)；（2）NNG算法进行图像合并必须构造邻接矩阵，若初始分割得到k个区域则最大时间复杂度为O(k!)，若迭代次数为k1则合并总的时间复杂度为O(k1×k!)。总的时间复杂度为O(m×n+k1×k!)，其计算时间复杂性主要集中在利用NNG合并时构造的邻接图上，因此减少区域块是提升时间复杂度的主要途径。

4 结论

首先采用了改进的最小生成树方法对图像进行分割，其次利用了NNG方法对初分割后的图像进行合并。本文方法减少了最小生成树的构造过程，节省了分割时间，通过合并使过分割的区域得到了有效的减少，较好地保留了全局信息。但是利用NNG方法进行迭代合并时，迭代次数影响着分割的效果，关于迭代次数的确定还需要进一步探讨。

[1]孙即祥.图像分析[M].北京：科学出版社，2005.

[2]Shi J，Malik J.Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（8）：888-905.

[3]Suk M，Cho T H.Segmentation of images using minimum spanning tree[J].Applications of Digital Processing V，1983，397：180-185.

[4]Boykov Y，Jolly M P.Interactive graph cuts for optimal boundary and region segmentation of objects in N-D images[C]//Proceedings of International Conference on Computer Vision，2001：105-112.

[5]Zahn C T.Graph theoretical methods for detecting and describing gestalt clusters[J].IEEE Trnas on Computers，1997，20（1）：68-86.

[6]Haddon J F，Boyce J F.Image segmentation by unifying region and boundary information[J].Transactions on Pattern Analysis and Machine Intelligence，1990，12（10）：929-948.

[7]叶伟，王远军.基于Mumford-Shah理论的最小生成树图像分割方法[J].计算机辅助设计与图形学学报，2009，21（8）：1127-1134.

[8]Cha B，Suetake N，Kawano H，et al.Fast minimum-spanningtree-likeimagesegmentation[C]//Proceedingsofthe4th International Conference on Natural Computation，2008：152-156.

LI Ying,DAI Fang,HAO Yong,ZUO Tao

School of Science,Xi’an University of Technology,Xi’an 710054,China

Based on minimum spanning tree,a method of image segmentation using improved minimum spanning tree is presented.The procedure of generating minimum spanning tree is reduced,and then the similarity-based neighborhood graph method is applied to merge image split by minimum spanning tree.The proposed method saves the time of image segmentation,meanwhile,based on the effective merger the better segmentation results are obtained.

minimum spanning tree;NNG（Nearest Neighbor Graph）method;image segmentation

基于最小生成树思想，给出了一种利用改进的最小生成树进行图像分割的方案，减少了最小生成树的构建过程，对初分割的结果利用NNG算法进行合并。该方案节约了分割时间，并且对分割后的图像进行了有效的合并，达到了较好的分割效果。

最小生成树；相似邻近图；图像分割

A

TN911.73

10.3778/j.issn.1002-8331.1111-0064

LI Ying,DAI Fang,HAO Yong,et al.Image segmentation based on minimum spanning tree.Computer Engineering and Applications,2013,49（13）：149-151.

黎莹（1986—），女，硕士研究生，主要研究领域为智能计算与信息处理；戴芳（1966—），女，博士，教授，硕士生导师，主要研究领域为智能计算与信息处理。E-mail：li_ying1108@126.com

2011-11-08

2012-01-02

1002-8331（2013）13-0149-03

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1722.087.html