扭立方体连接网络结构的研究与分析

王新阳，梁家荣

广西大学 计算机与电子信息学院，南宁 530004

扭立方体连接网络结构的研究与分析

王新阳，梁家荣

广西大学 计算机与电子信息学院，南宁 530004

1 引言

超立方体网络是一种优秀的网络结构，为使其具有更广泛的适用范围，人们针对其自身的结构特点提出了诸多超立方体网络变体结构，如增强的超立方体网络，扩展超立方体网络，广义超立方体网络，Möbius立方体网络[1-2]，交叉立方体网络[3-5]，扭n-立方体网络[6]，扭立方体网络[7-8]，局部扭立方体网络[9]，广义扭立方体网络[10]，扭立方体连接网络[11]，spined立方体网络[12]等。这些变体结构在顶点/边数、正则性、连通度、递归性等方面都与超立方体相同或接近，同时，其在不改变网络连接复杂度的基础上相比超立方体网络大大降低了网络的直径，如n维Möbius立方体、交叉立方体、扭立方体、扭立方体连接网络等网络的直径为，这几乎是n维超立方体网络直径的一半；另外，广义扭立方体网络直径为，spined立方体网络当n≥14时直径为

研究各种超立方体变体网络对丰富和发展超立方体网络具有重要的学术意义和实际应用价值。在超立方体的诸多变体结构中，交叉立方体网络以其优越的结构特点获得了最为广泛而深入的研究，是超立方体网络最为重要的变体之一。借助于交叉立方体网络的结构，文献[11]中提出的扭立方体连接网络由于具有与交叉立方体网络比较相似的拓扑结构，同样受到广泛关注。但是，在进一步研究和实际应用中，发现扭立方体连接网络的定义不够严谨，网络中结点并不能像定义中规定的那样实现正确连接，当n≥5时，扭立方体连接网络是部分不连通的。本文结合交叉立方体网络和扭立方体连接网络的定义，证明并举例分析了扭立方体连接网络是不连通的；并在此基础上，提出了一种新的网络结构——扭交叉立方体网络(TCQn)。接着，初步研究了TCQn的正则性、连通度、容错度、递归性等网络性质。研究表明，TCQn具有与CQn一样的网络性质，是一种优秀的网络结构。

2 相关知识

本文的术语与标记与图论中的一致。设G为一个无向图，V(G)和E(G)分别表示图G的顶点集和边集。图G中的顶点用二进制字符串表示。e(u，v)表示图中连接相邻两个顶点u与v的边；σ(u)=i表示对于顶点u，un=un-1=…= ui+1=0且ui=1；εi表示二进制字符串第i位为1，其余为0。

定义1[2-3]设x=x2x1，y=y2y1是两个二进制串，称x与y是一个关联对，当且仅当

记为x～y。

本文规定，若x～y，则x与y间的关系还可以表示为y=RC(x)或x=RC(y)。

定义2[2-3]n维交叉立方体(CQn)是一个n-标号图，CQ1是一个顶点分别被标为0和1的两点完全图K2；当n≥1时，CQn由两个(n-1)维交叉立方体和构成，其中：

1～4维扭立方体连接网络，如图1所示。

图1 1～4维扭立方体连接网络

定义4[11]∀u，v∈V(TNn)，若u与v在TNn中邻接且σ(x+y)=i，则称u与v是第i维邻接的，记为v=fi(u)。

3 扭立方体连接网络的结构分析

根据定义2可以得到交叉立方体的互连函数，即定理1。

定理1[13]若x，y∈V(CQn)，σ(x+y)=i，则当且仅当x与y满足以下关系式时(x,y)∈E(CQn)，即x与y在CQn中相邻接。

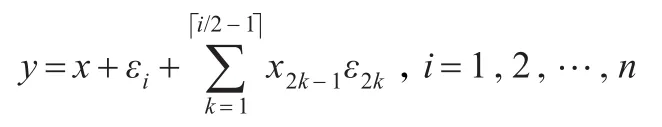
类似地，根据扭立方体连接网络的定义可直接得到扭立方体连接网络的互连函数，即定理2。

定理2[11]若x，y∈V(TNn)，σ(x+y)=i，则当且仅当x与y满足以下关系式时(x，y)∈E(TNn)，即x与y在TNn中相邻接。

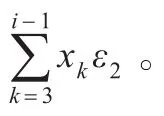
（1）利用关联对的概念，按照交叉立方体的连接方式对x进行变换得到y′。

以下将证明扭立方体连接网络TNn是部分不连通的。

定义5∀u=unun-1…u1，v=vnvn-1…v1，σ(u+v)=i，若当时，存在k，使得s≤k≤t时，有u2ku2k-1～ v2kv2k-1，则称对u的第2s-1维到第2t-1维进行了关联变换，记为RCu(s，t)，并记u2ku2k-1RCu(k，k)。

引理1对于∀u=unun-1…u1，v=vnvn-1…v1，若v= RCu(s，t)，则必有u=RCv(s，t)。

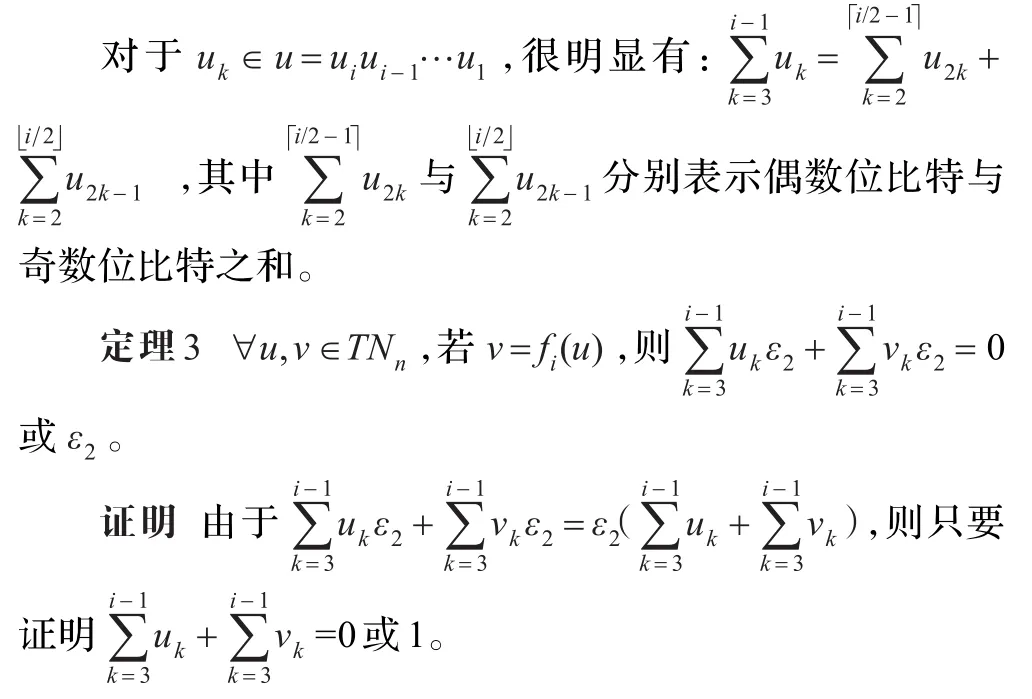
证明利用反证法进行证明，假设命题成立，令v=fi(u)，uu=fi(v)，则命题转化为证明u=uu。根据定理2，定义4、5及引理1，如果v=fi(u)，则可得：

于是有以下定理：

定理5当n≥5时，TNn是不连通的，不连通结点数为TNn结点数的一半。

以下举例说明TNn是不连通的。

例1u=00101，可以通过两种方法得到v=f5(u)并证明u≠f5(v)。

4 改进的网络结构——扭交叉立方体网络（TCQn）

定义6n维扭交叉立方体网络(TCQn)是一个n-标号图，TCQ1是一个顶点分别被标为0和1的两点完全图K2；当n≥1时，TCQn由两个(n-1)维扭交叉立方体TCQ(0)n-1和构成，其中，

根据扭交叉立方体网络(TCQn)的定义可以得到其互连函数，即定理6。

定理6若x,y∈V(TCQn)，σ(x+y)=i，则(x,y)∈E(TCQn)（即x与y在TCQn中相邻接），当且仅当x与y满足以下关系式：

证明根据定义6关于TCQn的定义过程可知，若x与y在TCQn中邻接，且σ(x+y)=i，则当时，x2kx2k-1～y2ky2k-1。根据关联对的定义，x2kx2k-1与y2ky2k-1只能为以下取值之一：(x2kx2k-1，y2ky2k-1)∈{（00，00），（10，10），（01，11），（11，01）}。可以观察到，此时x2kx2k-1与y2ky2k-1满足关系：

1～4维扭交叉立方体与扭立方体连接网络一样，见图1，5维扭交叉立方体如图2所示。

图2 5维扭交叉立方体TCQ5

定义7∀u,v∈V(TCQn)，如果u与v相邻且σ(u+v)=i，则称u与v在第i维上邻接，记为u=Ni(v)。

定理7n维扭交叉立方体TCQn是连通的。

证明∀u,v∈V(TCQn)，令v=Ni(u)，uu=Ni(v)，要证明网络是连通的，只要证明uu=u即可。由图1易知，当1≤n≤4时，TCQn是连通的；当n≥5时，类似于定理4的证明过程有：

从扭交叉立方体TCQn的构造过程可以看到，扭交叉立方体与交叉立方体的连接方式不仅相似，而且具有极大的互补性，是交叉立方体结构的重要补充。因此，扭交叉立方体既可以看做超立方体的变体结构，也可以当成交叉立方体的变体，甚至可以看做与交叉立方体具有同等重要作用的一种新型网络结构。以下研究TCQn的一些基本网络性质。

定理8TCQn是n-正则图。

证明根据TCQn的定义可知，TCQn中任一顶点u有且仅有一个顶点与其在第i维上相邻，并且这种相邻是对称，所以有Δ(G)=δ(G)=n，即TCQn是n-正则的。证毕

定义8[6]设G1和G2是两个阶数相同的图：V(G1)={u1，u2，…，up}，V(G2)={v1，v2，…，vp}。令H=G1⊙G2，其中，V(H)= V(G1)∪V(G2)，E(H)=E(G1)∪E(G2)∪{(ui，vi)|ui∈V(G1)，vi∈V(G2)，1≤i≤p}。

引理2[6]令G1和G2为定义8中的两个连通图，H=G1⊙G2，则

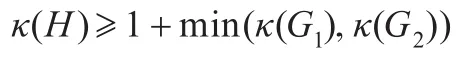
引理3[14]对任意图G，都有：κ(G)≤κ'(G)≤δ(G)。

定理9κ(TCQn)=κ'(TCQn)=n。

证明根据TCQn的定义可知，TCQn=TCQn-1⊙TCQn-1，由引理2有：

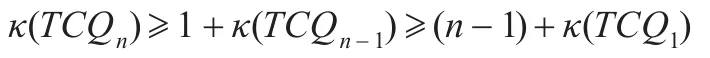
易知κ(TCQ1)=1，所以κ(TCQn)≥n。又由引理3及定理8有：κ(G)≤κ'(G)≤δ(G)=n，综合得κ(TCQn)=κ'(TCQn)=n。证毕

引理4[14]（Whitney定理）一个非平凡图G是k连通的(k≥2)当且仅当对于G的任意两个顶点u、v，G至少有k条内部不相交的u-v的路。

由定理9和引理4可得以下推论：

推论1TCQn中任意两个顶点u、v之间存在n条顶点不相交的路径。

关于网络的容错能力，还可以通过顶点容错度和边容错度来衡量。

定义9TCQn的顶点容错度定义为min{k-1||X|=k，X为TCQn的点割集}，记为TV(TCQn)；TCQn的边容错度定义为min{k-1||Y|=k，Y为TCQn的边割集}，记为TE(TCQn)。

定理10TV(TCQn)=TE(TCQn)=n-1。

证明由于TCQn是一个正则图，最少要去掉n条边，才能使TCQn不连通，同时注意到，去掉某个顶点关联的n条边后，TCQn也不连通，因此TE(TCQn)=n-1；由定义9及点连通度的定义可知Tv(TCQn)=κ(TCQn)-1，又由定理9有κ(TCQn)=κ'(TCQn)=n，所以TV(TCQn)=n-1。证毕

记Γα(G)为图G中前缀为α的所有顶点构成的子图。

定义10[15]设G是一个n-标号图，即图中每个顶点使用一个长度为n的二进制字符串进行标记，*n-i是长度为n-i的二进制串，*∈{0，1}，i=1，2，…，n，如果Ri是Γ*n-i0(G)到Γ*n-i1(G)的一一映射，则称Ri是G上的一个i维二进制互联函数。

定义11[15]设G是一个n-标号图，Ri是G上的i维二进制互联函数（i=1，2，…，n）。∀x，y∈V(G)，如果(x,y)∈ E(G)当且仅当∃k∈{1,2,…,n}，使得y=(x)，则称G为由R1，R2，…，Rn确定的n维二进制递归互联网络。

定理11TCQn属于n-维二进制递归网络。

证明易知TCQn为n-标号图。根据定理6可知，∀i∈{1，2，…，n}，存在映射Ri使得Γ*n-i0(G)=Ri(Γ*n-i1(G))。根据定义6，对于∀u∈Γ*n-i0(G)，在Γ*n-i1(G)中有且仅有一个点v与之相连；同样，对于∀v∈Γ*n-i1(G)在Γ*n-i0(G)中也有且仅有一个点u与之相连，则Ri是Γ*n-i0(G)到Γ*n-i1(G)的一一映射，因此Ri是TCQn上的一个i维二进制互联函数。∀x,y∈V(TCQn)，如果∃k∈{1，2，…，n}，使得y=(x)，由定义6及定义10可得(x,y)∈E(TCQn)；另一方面，若(x,y)∈E(TCQn)，由定理6可得∃k∈{1，2，…，n}，使得y=Nk(x)=(x)。根据定义11可知TCQn是由R1，R2，…，Rn确定的n-维二进制递归网络。证毕

由于TCQn属于二进制递归网络，因此具备二进制递归网络的所有性质，如前面已证明的TCQn为n-正则图，连通度为n，容错度为n-1，此外，还有如网络直径的界D(TCQn)不超过n，以及TCQn的核度、坚韧度、离散度等参数的范围。此外，TCQn还具有二进制递归网络的递归特性，如TCQn中的i维子网总是由更小的i-1维子网递归构成，子网之间具有类似于网络结点的邻接关系等。

除了上述性质外，TCQn还具有其他网络所具有的结构性质，如含有3-立方体。

超立方体及其变体网络是由3维网络连接构成，如果仅考虑同构关系，3维网络可以分为3-立方体和3-扭立方体，如图3所示。

图3 3维立方网络

这些立方体相互连接，递归地构成了更高维网络。在超立方体及其已知的变体结构（如扭n-立方体、广义扭立方体、Möbius立方体、交叉立方体等）中，都含有3-立方体。根据TCQn的定义，可得TCQ4立体结构如图4所示。

图4 TCQ4立体结构

容易看出，在TCQ4中不存在3-立方体。但是当n≥5时，在TCQn中是存在3-立方体的，举一个例子即可说明结论。如在TCQ5中，4长环＜00000，10000，11000，01000＞与＜00010，10010，11010，01010＞构成了一个3-立方体。

5 结束语

交叉立方体网络以其优越的结构特性得到了广泛的研究和应用，是一种非常优秀和重要的网络互连结构。扭立方体连接网络由于结构与交叉立方体网络比较接近，因此也具备交叉立方体网络的某些良好特性。本文结合交叉立方体网络的构造原理，分析了扭立方体连接网络的结构特点，发现扭立方体连接网络的连接方式存在问题，证明了当n≥5时，TNn是部分不连通的，并且不连通的结点是TNn网络总结点数的一半。同时，本文通过对扭立方体连接网络结构特点的分析，提出了一种新型网络结构——扭交叉立方体网络TCQn，证明了扭交叉立方体网络是完全连通的，研究了TCQn的正则性、连通度、容错度、递归性等网络性质。研究表明，TCQn具有与CQn一样的网络性质，是一种优秀的网络结构。TCQn在结构上与交叉立方体网络具有相似性，并且两者在连接方式上是完全互补的。

鉴于扭交叉立方体网络与交叉立方体网络在结构上的相似性和连接方式上的互补性，扭交叉立方体网络无疑也是一种理想的网络结构，因此，有必要进一步研究扭交叉立方体网络的结构特点，找出其相对于交叉立方体网络更好的网络参数，并充分利用其与交叉立方体网络连接方式的互补性，实现更优的网络连接。

[1]Tsai Changhsiung.Embedding of meshes in Möbius cubes[J]. Theoretical Computer Science，2008，401：181-190.

[2]Zhou Shuming.The conditional diagnosability of Möbius cubes under the comparison model[C]//Proceedings of the 2009 IEEE International Conference on Information and Automation，2009：96-100.

[3]Efe K.The crossed cube architecture for parallel computation[J].IEEE Trans on Parallel and Distributed System，1992，3（5）：513-524.

[4]Dong Qiang，Yang Xiaofan，Zhao Juan，et al.Embedding a family of disjoint 3D meshes into a crossed cube[J].Information Sciences，2008，178：2396-2405.

[5]Dong Qiang，Yang Xiaofan.Embedding a long fault-free cycle in a crossed cube with more faulty nodes[J].Information Processing Letters，2010，110：464-468.

[6]Esfahanian A H，Ni L M，Sagan B E.The twisted N-cube with application to multiprocessing[J].IEEE Trans on Computer，1991，40（1）：88-93.

[7]Lai Chiajui，Tsai Changhsiun.Embedding a family of meshes into twisted cubes[J].Information Processing Letters，2008，108：326-330.

[8]Dong Qiang，Yang Xiaofan，Wang Dajin.Embedding multidimensional meshes into twisted cubes[J].Computers and Electrical Engineering，2010，36：1021-1026.

[9]Li Tsengkui，Lai Chiajui，Tsai Changhsiubg.A novel algorithm to embed a multi-dimensional torus into a locally twisted cube[J].Theoretical Computer Science，2011，412：2418-2424.

[10]Cull P，Larson S M.On generalized twisted cubes[J].Information Processing Letters，1995，55：53-55.

[11]Wang Deqiang，Zhao Lianchang.The twisted-cube connected networks[J].J Comput Sci&Technol，1999，14（2）：181-187.

[12]Zhou Wujun，Fan Jianxi，Jia Xiaohua，et al.The spined cube：a new hypercube variant with smaller diameter[J].Information Processing Letters，2011，111：561-567.

[13]Zhao Lianchang，Wang Deqiang，Yang Suqin，et al.On the equivalent definition and sub-cube adjacent properties of the crossed cube[J].Journal of Dalian Maritime University，2001，27（3）：57-60.

[14]Chartrand G，Zhang Ping.Introduction to graph theory[M].北京：人民邮电出版社，2007.

[15]孙云，李舟军，王德强.二进制立方形递归网络的拓扑结构[J].计算机研究与发展，2008（z1）：179-184.

WANG Xinyang,LIANG Jiarong

College of Computer Science and Electronic Information,Guangxi University,Nanning 530004,China

Referring to the structure of the crossed cube（CQn）and the definition of pair-related,this paper analyzes the structure character of the twisted-cube connected network（TNn）,and proves that TNnis disconnected forn≥5and the number of the disconnected nodes is half of nodes in the network.Besides,by analyzing the problems of the twisted-cube connected network, it obtains a new network structure:the twisted crossed cube（TCQn）,proves that the network is all connected,and makes some preliminary studies on its basic network properties,such as the regularity,connectivity,fault tolerance,recursiveness,and so on, which indicates that the TCQnhas the same excellent network properties as the CQn.

pair-related;crossed cube;twisted-cube connected network;twisted crossed cube

根据交叉立方体（CQn）的结构与关联对的概念，对扭立方体连接网络（TNn）的结构特性进行了分析，证明了当n≥5时，TNn是不连通的，并且不连通的结点数占整个网络结点数的一半。通过分析扭立方体连接网络的错误所在，提出了一种新型网络结构——扭交叉立方体（TCQn），证明了该网络结构是完全连通的，初步研究了其基本网络性质，如正则性，连通度，容错度，递归性等，表明TCQn具有与CQn同样优秀的网络性质。

关联对；交叉立方体；扭立方体连接网络；扭交叉立方体

A

TP393

10.3778/j.issn.1002-8331.1110-0579

WANG Xinyang,LIANG Jiarong.Research and analysis on structure of twisted-cube connected network.Computer Engineering and Applications,2013,49（13）：93-99.

国家自然科学基金（No.61064002）；教育部“新世纪优秀人才支持计划”（No.NCET-06-0756）。

王新阳（1985—），男，博士，研究方向为计算机网络拓扑性质，并行计算，云计算；梁家荣（1966—），男，博士，教授，博士生导师，研究方向为无线传感器网络，网络可靠性分析。E-mail：wxyyuppie@139.com

2011-10-28

2012-03-31

1002-8331（2013）13-0093-07

◎数据库、数据挖掘、机器学习◎