多元切比雪夫神经网络及其快速权值确定算法

邢永康，石杨，牟超

重庆大学 计算机学院，重庆 400030

多元切比雪夫神经网络及其快速权值确定算法

邢永康，石杨，牟超

重庆大学 计算机学院，重庆 400030

1 引言

人工神经网络目前发展很快，鉴于多层感知器（Multilayer Perceptron，MLP）神经网络后向传播（Back Propagation，BP）算法的不足，文献[1]基于函数逼近理论提出了一种全新结构的神经网络——切比雪夫神经网络。切比雪夫神经网络是一个拥有单隐藏层的神经网络，目前已经证明，切比雪夫神经网络拥有强大的表示能力[2-3]，相比多层感知器神经网络，其收敛速度更快，计算复杂度也较低，而且具有良好的泛化性[4-6]。

目前切比雪夫神经网络的收敛算法主要为一元函数下的收敛算法，较为广泛使用的是梯度下降算法[6]。该算法存在有速度过慢，不能很好的收敛，步长不能直接确定等问题。很多学者对该问题进行研究。文献[7]提出了权值的直接确定法，但需要进行高阶的矩阵求逆工作；文献[8]提出使用三次样条插值方法重构输入样本，使其适合于切比雪夫多项式，但复杂度依旧较高；另外，当前较为流行的SVM由于需要求解线性方程组[9]，同样需要花费较多的时间。

实际应用中，很多问题都是建立在多元函数基础上的，需要把该网络推广到多元函数下，扩大适用范围，另外需要寻找一种有效的方法，快速确定切比雪夫神经网络的权值。据此，提出了多元函数下的切比雪夫神经网络模型，并在切比雪夫多项式的正交性的基础上给出了多元函数下切比雪夫神经网络的快速权值算法。该算法需要使用切比雪夫多项式的零点，而在很多问题当中，切比雪夫多项式的零点不适合或者不方便求得，为了使算法更具有普遍性，在仿真实验中采用正交多项式重构输入样本，达到使用切比雪夫正交性质的要求。实验结果表明，本文的神经网络模型可以很好地拟合多元函数，并且在计算速度上相对于传统算法有较大的提高。

2 一元切比雪夫神经网络

2.1 一元切比雪夫神经网络的概念

传统的MLP神经网络通常采用BP算法，采用该算法的MLP神经网络被称为BP神经网络，但是基于BP算法的MLP神经网络存在着缓慢收敛与局部最小值等缺点。切比雪夫神经网络模型与MLP神经网络模型完全不同，其结构如图1所示。

图1 一元切比雪夫神经网络

图1中，xr为输入值，yr为对应的输出值，相应的函数为yr=f(xr)(r=1，2，…，n)；Ti为构成隐含层的切比雪夫k次多项式，Ck为对应Tk的权值，由函数逼近理论可知，f(xr)可以通过采用已知的基函数来进行线性拟合，文中，采用的是已知的切比雪夫多项式来进行线性拟合，即寻找一个多项式Qm(xr)：

使Qm(xr)能够有效地逼近yr=f(xr)。

切比雪夫神经网络的理论基础来自于切比雪夫多项式以及最小平方逼近概念，下面给出切比雪夫多项式的定义。

定义1n次切比雪夫递推多项式定义为：

由式（2）得到定义2的多项式组。

定义2递推关系下的切比雪夫多项式组：

由函数逼近性质可知，只需计算出Tk所对应的Ck，即可对未知函数进行有效逼近，该多项式组的收敛性质由下面的最小平方收敛定理所保证，令

则ε为多项式逼近与目标函数的误差。由最小平方逼近的概念，只需使每个样本点上误差函数的第二范数平方之和最小，即使

最小，其中E被称为逼近函数在xr上的误差平方和。

下面的定理给出了最小平方逼近的存在且唯一的理论依据，它保证了切比雪夫神经网络的逼近能力。

显然，不同阶切比雪夫多项式之间线性无关，满足定理1，即在最小平方逼近下Ci存在且唯一。

即Ct(m+1)=Ct(m)-ΔCt。其中，η为学习步长，一个较小的学习步长可以保证收敛而不至于越过最小值，但相应的会使计算量大为增加。

2.2 一元切比雪夫神经网络的快速算法

在介绍切比雪夫神经网络快速权值确定算法前，需要先给出切比雪夫多项式的一个重要性质：正交性。一般来说，切比雪夫的正交性分为两种：连续状态下的正交性与离散状态下的正交性。以下是针对离散的点上切比雪夫的正交性定理。

定理2（切比雪夫多项式正交定理）

任意两个相异的切比雪夫多项式Tr(x)及Ts(x)(r,s≤n)在Tn+1(x)的零点集

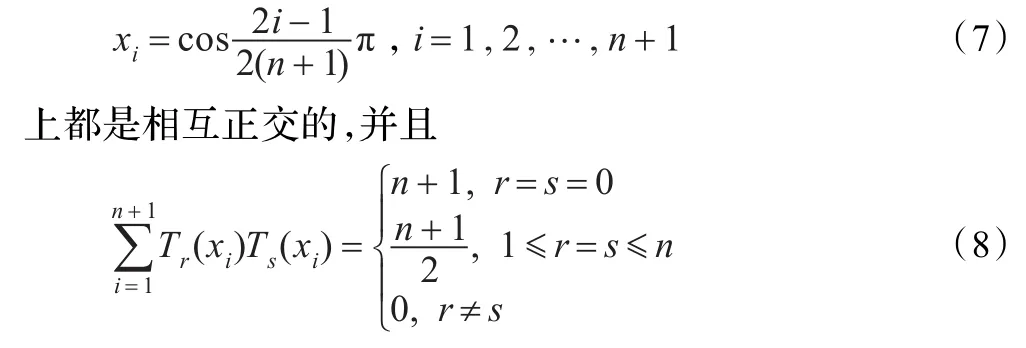
这说明，只要在零点集上，就可以利用切比雪夫多项式的正交性，极大地改善计算复杂度。

由公式（6），若使E取到最小值，需要满足以下条件：

由定理2的正交性，可得：

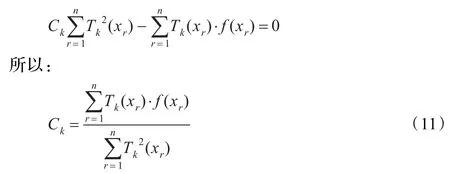
式（11）为一元函数下切比雪夫神经网络权值的直接确定公式，显然，由于正交性的使用，计算被大为简化，并且保证了权值为全局最优。

3 多元切比雪夫神经网络

3.1 多元切比雪夫神经网络的定义

在一元切比雪夫神经网络的结构与理论基础上，将其推广到多元函数下，其中输入为n维向量x1,x2,…,xn，需要逼近的目标函数为，要求是寻找一个多项式：

其中，k1k2…kn分别为n个不同的数，每个数的取值都是从0开始，且上界不一定相同。T1，T2，…，Tn分别表示不同的切比雪夫多项式，每个切比雪夫多项式从0次开始，上界由m确定。

以二元函数为例，输入为xr和yr，需要逼近的未知函数为f(xr，yr)，用于拟合xr的切比雪夫多项式有m项，用于拟合yr的切比雪夫多项式有n项，则切比雪夫神经网络结构图，如图2所示。

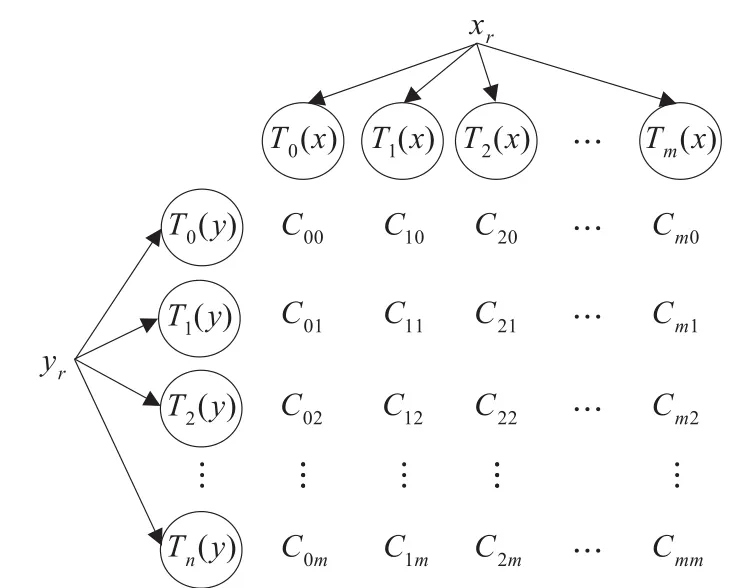
图2 二元函数切比雪夫神经网络结构

下面是多元切比雪夫神经网络的梯度下降迭代算法，在多元函数下，由最小平方逼近理论构造误差函数为：

该误差函数的第二范数平方和为：

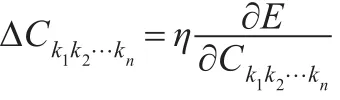
显然，Ct1t2…tn(m+1)=Ct1t2…tn(m)-ΔCt1t2…tn，其中η为学习步长。

可以看到，随着输入函数未知量的增加，该权值计算变得相当复杂，复杂度呈指数级的上升。这说明，在面对多元输入函数时，普通的梯度下降迭代算法不再适用于切比雪夫神经网络。

3.2 多元切比雪夫神经网络的快速权值确定算法

首先对定理2进行推广，由于多元切比雪夫神经网络针对每个元均维持一组切比雪夫多项式组，且彼此之间互相独立，所以得定理3。

定理3任意两个相异的切比雪夫多项式Tr(x)及Ts(xn) (r，s≤n)在Tn+1(xn)的零点集

其中，n表示第n个元，依据定理3，在每个元的零点集上，可以利用切比雪夫多项式的正交性快速确定权值。

式（19）即为多元函数下切比雪夫神经网络的权值快速计算法。

4 仿真实验

4.1 样本点的预处理

由式（7）可知，切比雪夫多项式的零点集是有条件的，如何将随机选取的点集一一对应到切比雪夫多项式零点集是需要考虑的重要问题，这里采用函数逼近的另一种方法，将切比雪夫神经网络扩展为两个独立的部分，如图3所示。

图3 正交多项式组与切比雪夫神经网络

4.2 实验及结果分析

为进行对比，基于BP算法的切比雪夫神经网络步长取0.001，最高拟合次数为20 000次，基于BP算法的MLP神经网络的步长为0.01，隐含层节点数目为32个，为单隐含层神经网络，训练精度均为0.001。从表1可以看出，本文算法在多元函数下，其时间性仍然优于传统算法。

表1 不同输入时本文算法与传统算法的时间性对比

表2是这几种算法的误差在x=5，y=10训练样本上的训练结果与需要拟合函数误差的绝对值和。可以看出，本文算法在多元函数下误差依旧较低，这说明，本文算法可以良好地回忆起训练内容。

表2 本文算法与其他算法的误差对比

由于基于BP算法的切比雪夫神经网络在计算复杂度上同基于BP算法的MLP神经网络一样，其计算复杂度对于需要更新的权值数目而言是多项式级的。但是同样，该切比雪夫神经网络也继承了基于BP算法的MLP神经网络的缺点，BP算法对于梯度是即时计算的[10]，且步长往往需要通过经验来判断。另外，从计算时间上来讲，这种算法并没有一个明确的值，不能在训练之前就得出相应的时间代价。

本文所使用的样本预处理方法基于正交化理论，虽然相对于传统的切比雪夫神经网络算法，增加了一部分正交多项式的计算，但其计算复杂度有限，且计算规模可以在计算前判定。而且在切比雪夫神经网络部分，完全是多项式计算，因此其计算速度远高于传统算法。

5 结束语

切比雪夫神经网络应用广泛，本文将其由一元函数推广到多元函数下，进一步增加了切比雪夫神经网络的适用范围。同时为了克服基于BP算法的切比雪夫神经网络训练算法收敛速度慢的缺点，提出了一种新的方法改善切比雪夫神经网络的权值计算速度。仿真实验表明，改进后的切比雪夫神经网络模型在保证原有精度的情况下，其计算速度比传统算法有着明显的优势。

[1]Namatame A，Ueda N.Pattern classification with Chebyshev neural networks[J].International Journal of Neural Networks，1992，3：23-31.

[2]Purwar S，Kar I N，Jha A N.On-line system identification of complex systems using Chebyshev[J].Neural Networks Applied Soft Computing，2007，7：364-372.

[3]Akritas P，Antoniou I，Ivanov V V.Identification and prediction of discrete chaotic maps applying a Chebyshev neural network chaos[J].Solitons and Fractals，2000，11：337-344.

[4]张代远.基于分布式并行计算的神经网络算法[J].系统工程与电子技术，2010，32（2）：386-391.

[5]Shailc F A，Purwar S，Pratap B.Real-time implementation of Chebyshev neural network observer for twin rotor control system[J].Expert Systems with Applications，2011，38：13043-13049.

[6]Lee T T，Jeng J T.The Chebyshev-polynomials-based unified model neural networks for function approximation[J].IEEE Transactions on Systems Man and Cybernetics：Part B Cybernetics，1998，28（6）.

[7]张雨浓，李巍，蔡炳煌，等.切比雪夫正交基神经网络的权值直接确定法[J].计算机仿真，2009，26（1）：157-161.

[8]张代远.基于广义Чeбышeв多项式的新型神经网络算法[J].系统工程与电子技术，2008，30（11）：2274-2279.

[9]Cortes C，Vapnic V.Support vector networks[J].Machine Learning，1995，20：273-297.

[10]Haykin S.Neural networks and learning machines[M].北京：机械工业出版社，2009.

XING Yongkang,SHI Yang,MOU Chao

College of Computer Science,Chongqing University,Chongqing 400030,China

Compared with the traditional multi-layer perceptron model,Chebyshev neural network has fast convergence,low complexity and generalization ability advantages.However,the one variable Chebyshev neural network to solve multivariate problems in the practical application is great limitations.For this problem,the paper extends and proposes multivariate Chebyshev neural network model and gives fast weight determination algorithm which base on Chebyshev polynomials orthogonal. The simulation results show that compared to traditional multi-layer perceptron neural network,the method has obvious advantages in the calculation accuracy and computing speed.

neural networks;Chebyshev polynomial;multivariate function;quick calculation of the weights

与传统的多层感知器模型相比，切比雪夫神经网络具有收敛速度快，复杂度低，泛化能力强等优点，但是，其研究最为广泛的一元切比雪夫神经网络在解决实际应用中的多元问题时存在着很大局限。鉴于此，对一元切比雪夫神经网络进行扩展，提出了多元切比雪夫神经网络模型，并在切比雪夫多项式正交性的基础上给出了快速权值确定算法。仿真实验证明，相对于传统多层感知器神经网络，该方法在计算精度和计算速度等方面都存在明显优势。

神经网络；切比雪夫多项式；多元函数；权值快速计算

A

TP183

10.3778/j.issn.1002-8331.1204-0250

XING Yongkang,SHI Yang,MOU Chao.Multivariate Chebyshev neural network and quick learning algorithm.Computer Engineering and Applications,2013,49（13）：36-39.

国家自然科学青年基金（No.60403009）；中央高校基本科研业务费资助（No.CDJZR10180021）。

邢永康（1971—），男，博士，副教授，研究领域为人工智能，分布式系统，软件工程；石杨（1988—），男，硕士研究生；牟超（1989—），男，硕士研究生。E-mail：shiyang0830@126.com

2012-04-16

2012-06-14

1002-8331（2013）13-0036-04

CNKI出版日期：2012-08-06http://www.cnki.net/kcms/detail/11.2127.TP.20120806.1438.007.html