小学生数学学习力：一种基于发散性思维的理解与诠释

●端木钰

学习是人类的基本活动。不同的人会有不同的学习状态、学习方法、学习过程、学习结果，这主要取决于每个人学习力的差异性。因为每个人的学习力，是其各方面能力的综合体现，不仅包含个人学习内容的宽度、广度、深度，还包含个人学习能力的综合素质、学习效率、学习品质，更包含个人将学习结果转化为生活应用，提升生活质量的水平。如何从基础教育的小学做起，选择怎样的视角认知、提升小学生数学学习力呢？这就成为当下小学数学教育需要回答的一个时代命题。

一、功利背景下小学生数学学习的现状追思

随着数字信息化时代的来临，数学教育获得了更好的发展前景，各种新媒体教学技术的应用更是为数学教学的改革提供了高位发展的可能，作为基础教育的数学学科学习内容和学习方式都发生了本质性的变化。数学学习目标更为明确、数学学习内容呈多元化发展趋势，数学学习方式更注重过程与结论并重，但是，我们也不得不面对现实，受社会大气候的影响，功利化的思想也切实冲击着学生们的数学学习。为了让孩子们有个好的发展前景，家长们不辞辛劳地送孩子去各种校外培训机构，孩子们也以自己的数学分数优异成为骄傲的资本。更有部分教师出现公开课与日常课两张皮的现象，公开课上新的理念满天飞，表面上热闹非凡，一说就会，结果是一做就错，隔天再重头来过，在现代科学技术的强大支撑下，数学教师的专业成长之路任重而道远。教师们有时会陷入一种迷茫混沌的状态，坠入在浮躁和飘摇不定的功利化世界中，表面的目标和追求掩盖了真实的教育教学意义，看似繁荣的数学教育表象之下孕育着价值危机。

此外，数学教育的质量测评虽已做了一些改革与尝试，但是大部分学校还是延续着统一试卷测试的质量评定模式，虽在试题上有了改良，但是分数考量仍是高高在上。为了分数，学习者和教育者要倍加努力，学困生在一次次困扰中失去自信，学优生在一次次“成功”后趾高气昂。为了满足“教育市场”的各种需求，师生们就象生产车间的熟练工，课内课外忙，校内校外忙，提优补差忙，奥数竞赛忙。一切种种都是为了“不能输在起跑线上”。

这种基于功利背景下的数学教育意义缺失和教学行为偏离，表面上看是师生对高分的一厢情愿，其深层则是对师生人性发展的漠视，更是对数学教育的亵渎。数学教育教学必须进行有效的教育价值回溯与内省，探寻提升小学生数学学习力的实践路径。

二、基于发散性思维的小学生数学学习力解读

作为基础教育的数学学科应该不断提升小学生数学学习力，使学生逐渐找到个性学习数学之路。小学生数学学习力是指在小学生数学学习过程中，以获得数学知识和技能的学习为基础，通过实践、体验、反思、环境影响等途径，促进数学学习品性的提升，以达到产生新的数学思维、新的数学行为为目的的动态能力系统，它是衡量一个人数学综合素养和数学竞争力的尺度。基于上述的理解，笔者以为：要想提升小学生数学学习力，必须关注个性，追求一种基于发散性思维的层级式学习格局。

（一）基于发散性思维的小学生数学学习力的意义

“发散性思维是通过对思维对象的属性、关系、结构等重新组合获得新观念和新知识，或者寻找出新的可能属性、关系、结构的创新思维方法”。简单理解，发散性思维就是一种对已有记忆的广泛搜寻并进行自我加工的思维形式，它要求学习者以一个核心概念为中心，从不同视角不同层面展开丰富而立体的认识，它强调的是“一种辐射、扩散和求异”。发散性思维是一种建立在每个学习者自己已有的数学经验、数学知识、数学思考、数学理解基础上的，是一种主动的、自觉的、自由的、自信的、积极的数学思维方式，它才可以实现在学习数学知识的同时获得每个人思维创造力的提升。它是“一种扩张力与向心力的辩证统一”。但是，在教学中也应关注到张弛有度、张弛有序、张弛有悟、张弛有理。它可以在数学学习中彰显每个学生的思维特质，具有浓郁的个性色彩。

基于发散性思维的小学数学学习力提升可以增强学生对客观世界的批判意识和批判能力、反省意识和反省能力、创新意识和创新能力，促进学习者不断地对自我学习回顾、监督、调整、完善，它是小学生作为人的发展的核心之所在。

（二）发散性思维对于提升小学生数学学习力的双重价值

发散性思维一般具有“全方位性、流畅性、变通性、独创性”的特点。它是在短时间内学习者调动自己的多种思维方式进行的综合性的活动，它可以使学习者触类旁通，直抵核心概念。发散性思维其实是一种基于生活背景与认知背景下的立体性思维，它可以促进小学生在数学学习力提升的过程中实现自我的突破与超越，建立不同思维间的关联。

发散性思维对于小学生数学学习力提升具有双重价值。一方面，发散性思维体现了小学生数学学习力的本源性价值。发散性思维，其目的是培养学习者的思维能力和创新能力，它可以通过知识在单位时间的流量与综合提升小学生数学学习力的动态衡量。另一方面，发散性思维体现了小学生数学学习力的自我实现价值。在动态系统生成的过程中，小学生们逐渐在数学学习中自我认同、自我发展、自我超越，使学习的路越走越宽。

（三）发散性思维在小学生数学学习力“三重境界”中的层级式格局

学习力的研究近年来在我国生根开花，其中《学习力结构释义》中将个体学习力分为三个层面进行讨论，即“借鉴性学习力、转变性学习力、创造性学习力”三重境界。将此三层应用在数学教学中，“借鉴性学习力”侧重的应该是学习者在他人已有数学经验获得中所发展的思维深刻性与广博性；“转变性学习力”则是在数学学习力提升中自我的内化与完善，体现数学思维的反省性和批判性；“创造性学习力” 则是最高境界，它是学习的终极目标，体现了数学思维的前瞻性和创新性。

发散性思维在小学生数学学习力的 “三重境界”中应该逐步建构出层级式的发展格局，以此建立一种数学学习的动态能力系统。具体如下表：

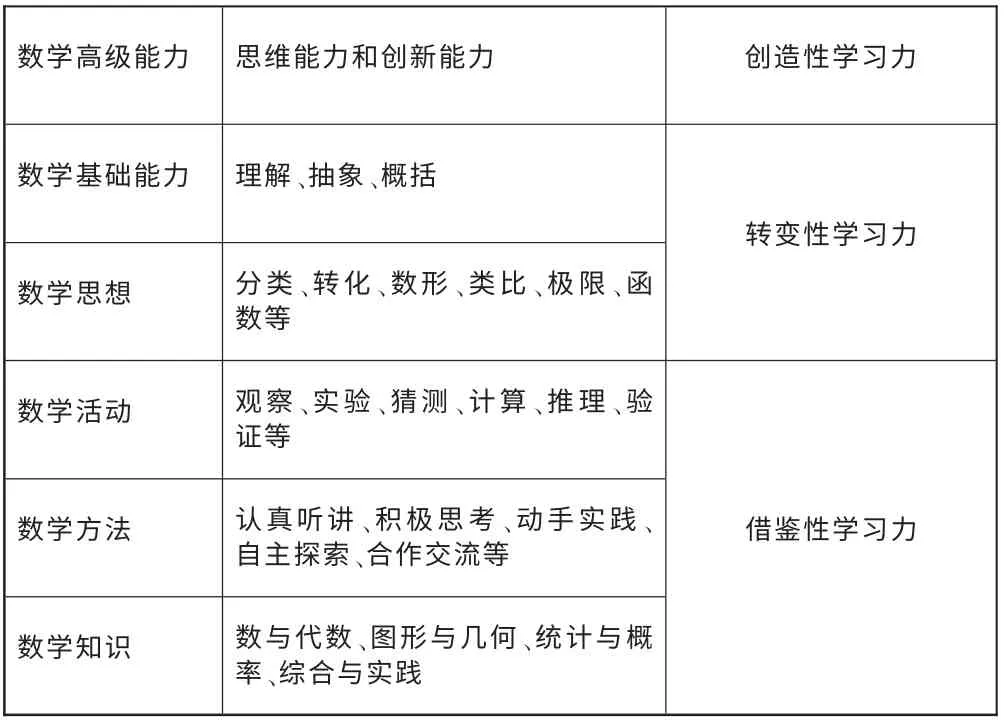
在上述的层级表里，新课标明确表达了小学生所掌握的数学知识、数学方法和数学活动，此三个层级应属于借鉴性学习力发展范畴；数学思想、数学基础能力和数学高级能力都是内隐的三个层级，它们中的前两者属于转化性学习力发展范畴，而思维能力和创新能力的发展才是数学学习的最高层面，属创造性学习力。《数学课程标准》（2011年版）明确指出：“数学教育既要使学生掌握现代生活和学习中所需要的数学知识和技能，更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。”

三、发散性思维提升小学生数学学习力的实践路径

基于发散性思维的理解提升小学生数学学习力，是一种对当下小学数学教育的变革性认知，是符合学生数学认知特点的一种积极性尝试。发散性思维可以让我们更现实地了解学生在数学学习中的思维发展真实方向，这种内在的思维状态在数学教学中必须通过一种外在的显性表达方式呈现，故笔者主持的团队选择了引导学生用思维导图进行发散性思维提升数学学习力的有效表达方式。这样，使发散性思维的内隐性与思维导图表达的外显性辩证统一，最终达成小学生数学学习力的提升，从而找寻师生作为独立思维生命体的意义与价值。

（一）思维导图引进数学教育教学的意义与价值

思维导图是20世纪60年代初，英国学者东尼·博赞（Tony Buzan）基于对脑神经生理科学的研究，逐渐形成的关于发散性思维及其图形表达的研究成果。它是一种表达发散性思维的有效图形思维工具，也是一种将发散性思考具体呈现化的方法。它运用图文并重的技巧，将进入大脑的核心信息作为一个中心球体表现，从这个中心球体可以放射出若干条分支理解，将核心词与每一分支的理解用层级图表现出来，并把主题关键词与图像、颜色等建立记忆链接。（如图）它可充分运用左右脑的机能，利用记忆、阅读、联想、思维的规律，将学习者习得的知识进行重组、建构、优化，从而开启学习者大脑的无限潜能。

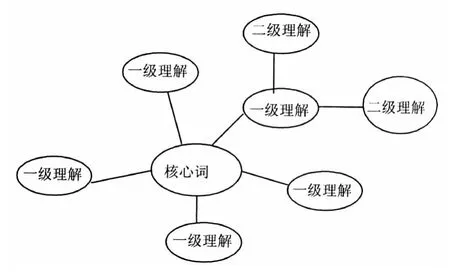
将思维导图的学习机理科学引入小学数学学习的教学，使学生在习得知识的同时，逐渐学会用自我整体建构的思维方式，走进思维过程、分析思维过程、发展思维过程，不断提升数学学习力，从而实现“数学、生活、儿童”的和谐发展，体现笔者学校原有“身边的数学”校本研究中“把数学还给热爱生活的儿童”的教育愿景，使学生们学会学习、学会生活。

（二）思维导图是提升小学生数学学习力的重要教学活动

思维导图可以将学习者隐性的思维过程外显化，通过思维导图可以观察、分析到学习者思维展开的过程、知识产生的结构，便于探寻学习者在思维活动的过程中知识迁移的方向、进程，更利于教师进行正确的引导、有效的教学。作为一种教学策略，思维导图可以贯穿一节课、一个单元；作为一种认识工具，思维导图可以使每位学生找到适合自己学习的坐标。思维导图可以较好的表现学习者思维动态变化的新陈代谢过程，新的学习结构不断产生，旧的学习结构不断被替代或消失，逐渐的发展学习者自身的数学学习思考力与创造力，有效提升学习力。

数学学习力提升建立在思维导图的学习方式之中，这种学习方式可以贯穿于教师的教学设计中、课堂实施中，也可以贯穿于学生的数学学习与生活中，从而实现思维导图提升小学生数学学习力的最终目标。正是通过学习者画出的思维导图引导他们不断的在数学思维发展进程中发现自我、审视自我、完善自我，从而实现数学学习力的提升。

思维导图的出现，不仅是作为一种教学或认知手段，更重要的是作为一种知识和对象的新的存在方式，新的教学策略，它衍生于对文本、思维想象的形象解读，使学习成为一种创造性的思维活动，使“书”与“图”的对立统一于“思维导图”，对于学习力提升具有重要价值。以学生画出的思维导图为切入点，分析学习者的思维特点，从而科学改进教与学的进程，最终实现小学生数学学习力的提升。

基于发散性思维理解下的小学生数学学习力，是通过师生对思维导图的外显性研究与内质性分析而进一步彰显学生个体思维进程的教与学探索。朝着此路前行，希望小学生们在学习数学的路上找到来时的路！

[1]郭黎岩，王东，田玲.提升中小学生学习力 基于脑科学的实践探索.中小学管理，2011，（9）：4-7.

[2]江萍萍，李姝.论课堂教学文化重构中学习力的生成.教育与教学研究，2011，（5）：38-42.

[3]刘斌祥，邹亚建.学习力结构释义.科技创业月刊，2007，（6）：131-132.

[4]陈维维，杨欢.教育领域学习力研究的现状和发展趋势.开放教育研究，2010，（4）：40-47.

[5]鲍健强，黄舒涵，蒋惠琴.论发散性思维和收敛性思维的辩证统一.浙江工业大学学报，2010，（6）：121-126.

[6]顾建达.数学发散性思维的特征及其培养.中学数学月刊，2000，（7）：6-8.

[7][英]东尼·博赞·巴利，博赞著.叶刚译.思维导图.中信出版社，2011.

[8]张海生.2001-2010年中外思维导图教育应用研究综述.中国电化教育，2011-8，120-124.

[9]刘晓宁.我国的思维导图研究综述.四川教育学院学报，2009，（5）：109-112.

[10]沈健强.概念图与思维导图的比较.浙江现代教育技术，2011，（6）：34-35.

[11]胡艺文，吴迪，陈绍东.教学中基于思维导图知识块建构研究.科技广场，2011，（7）：244-247.

[12]李良赞.论思维导图在新课程教学中的作用.新课程学习,2011,（4）：9-10.