压气机转子错频叶盘结构振动响应分析
徐可宁,王延荣,刘金龙
压气机转子错频叶盘结构振动响应分析
徐可宁1,王延荣2,刘金龙1
(1.中航空天发动机研究院有限公司,北京100028;2.北京航空航天大学能源与动力工程学院,北京100191)
利用三维叶轮机械气动弹性分析软件AEAS,对某压气机转子错频叶盘结构进行了振动响应分析,比较了各计算参数、错频量对数值仿真精度和效率的影响。结果表明,谐响应分析和瞬态响应分析,可得到错频叶盘结构各叶片的瞬态位移或动应力响应,进而获得各叶片的位移放大因子。通过研究错频对叶盘结构振动响应的影响,可指导错频叶盘的结构设计,并为降低由失谐导致的航空发动机叶盘结构高循环疲劳失效提供依据。
航空发动机;压气机转子;错频叶盘;谐响应;强迫振动响应;有限单元法
1 引言
由于材料和工艺限制,真实叶盘结构全都是失调的,而所谓的协调叶盘结构只是理想化的物理模型。但对于轻微失调的叶盘结构,可近似作为协调叶盘结构处理。一般叶盘结构的失调可分为被动失调和主动失调两大类。前者一般源于制造误差、材料分散性和使用磨损,后者指人为制造的叶片频差[1]。在气动弹性领域,错频叶盘结构往往可提高系统的气动弹性动稳定性,即在同一级转子上按一定规律控制各个叶片的频率分布来抑制颤振,这正是主动失调的一种典型应用。但错频破坏了原循环对称结构的周期性,可能会导致部分叶片的受迫响应振幅过大,即出现振动局部化现象,引起叶片高循环疲劳,在实际转子上表现为仅少数几片叶片发生断裂。
为了在预防颤振的前提下尽量抑制叶片的振幅放大,需要在设计阶段针对给定的错频方案,计算各叶片的位移或应力幅值,从而对振幅和应力放大因子进行评估。而计算各叶片的位移或应力幅值,需要进行强迫振动响应分析。如果对每个转速都进行强迫振动响应分析,其计算代价过大,因此可先通过谐响应计算进行初步分析,确定各叶片最大振幅出现时的转速,并在此转速下进行强迫振动响应分析,进而对错频叶盘结构的受迫振动状况进行评估。
本文使用北京航空航天大学开发的三维叶轮机械气动弹性分析软件AEAS[2],利用其中的有限元谐响应和瞬态响应分析模块,计算了某错频叶盘结构模型的振动响应。
2 计算模型
计算模型为如图1所示的带有31片叶片的压气机转子叶盘模型,设计转速为11 150 r/min,采用8节点实体单元划分网格,并在盘心前端施加轴向约束,同时在盘心后端施加周向约束。各叶片和盘的弹性模量E=210 GPa,泊松比μ=0.3,协调叶盘结构中盘和叶片的密度ρ=7 800 kg/m3。该叶盘结构的错频模式来自文献[3]的试验数据。在数值模拟中,采用调节各个叶片密度的方式实现错频,叶片密度和静频分布如图2所示。
3 压气机转子协调/错频叶盘结构谐响应分析
为确定各叶片在振动中的幅值,首先对转子叶盘结构进行谐响应分析。为确定谐响应分析的频率扫掠区间,需计算错频叶盘结构的Campbell图以确定共振频率,如图3所示。由于试验中发现,发生颤振的是1阶弯曲振型,因此所列出的是整个错频叶盘结构的前31阶频率(对应协调叶盘结构0~15节径的1阶频率)。在工作转速区域内,前31阶动频线与K=2的激振频率射线存在交点,因此下面的计算选取K=2,即采用2节径行波激励。此外,前31阶动频线与K=2的激振频率射线的所有交点对应的频率范围为215~246 Hz,因此选取谐响应的频率扫掠区间为200~261 Hz。谐响应计算中,在每个叶片的叶尖前缘同一节点施加2节径行波激励,激励力为随时间呈正弦变化的轴向集中载荷,阻尼都采用模态振型阻尼比的形式,所提取的谐响应幅值为各叶尖尾缘同一节点的周向位移。

图1 压气机转子叶盘结构有限元模型Fig.1 Finite element model of compressor blisk
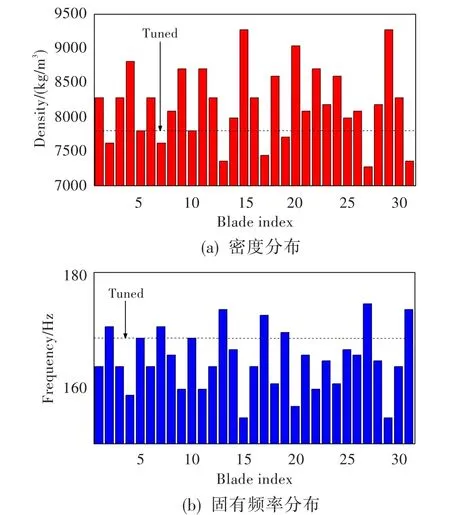
图2 错频叶盘结构各叶片的密度和固有频率分布Fig.2 Density and natural frequencies of each blade

图3 使用Campbell图确定的谐响应扫频区域Fig.3 Harmonic response swept-frequency region verified by Campbell diagram
但在谐响应计算中,扫掠频率间隔(计算中频率采样间隔,简称扫频间隔)对计算精度有较大影响,间隔过大,可能会漏扫峰值频率,导致计算峰值偏小;反之会增加计算量。此外,阻尼比、错频量及转速在叶盘结构振动响应计算中也有重要影响。下面分别对上述影响因素加以研究。
3.1协调叶盘结构谐响应计算中扫频间隔和阻尼比的影响
以60%设计转速为例,分别令扫频间隔为1 Hz、0.1 Hz、0.01 Hz和0.001 Hz,各阶模态振型阻尼比为0.01、0.005、0.001、0.000 5和0.000 1,进行谐响应计算。叶尖尾缘周向位移谐响应峰值及对应频率见表1。可看,对于协调叶盘结构,在其它条件相同时,当扫掠频率足够高且排除模态叠加误差的前提下,谐响应峰值与阻尼比成反比,且对峰值出现的频率没影响。当扫频间隔为0.01 Hz时,不同模态振型阻尼比计算得到的频谱图见图4。可见,阻尼越大,频谱图的峰值区域越平坦,对扫频间隔的敏感性越低。因此,对于协调叶盘结构的谐响应计算,可通过适当增加阻尼来加大扫频间隔,减小计算时间。
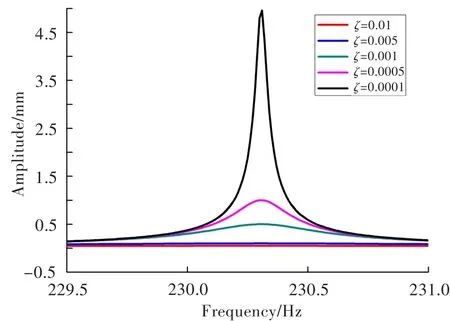
图4 不同阻尼比下协调叶盘结构的谐响应频谱图Fig.4 Harmonic response spectrogram of tuned bladed disk for different damping ratios
3.2错频叶盘结构谐响应计算中扫频间隔和阻尼比的影响
以60%设计转速为例,给定各阶模态振型阻尼比为0.001,分别以0.01 Hz、0.1 Hz和1 Hz作为扫频间隔,计算该转速下各叶尖尾缘周向位移的谐响应频谱,各叶片的峰值如图5所示。可见,阻尼比为0.001时,扫频间隔1 Hz与0.1 Hz某些叶片的峰值差别较大,而0.1 Hz与0.01 Hz每个叶片的峰值差别都较小。因此,以后计算中,当各阶模态振型阻尼比为0.001时,用0.1 Hz作为扫频间隔可满足精度要求。

图5 不同扫频间隔下错频叶盘结构各叶片的峰值Fig.5 Peak value of each blade on mistuned bladed disk with different swept-frequencies
对于错频叶盘结构,模态阻尼比对谐响应结果的影响比较复杂,计算所得的谐响应峰值与计算所采用的阻尼比不再是简单的反比关系,亦不能简单地通过增加阻尼的方式来加大扫频间隔、减少计算时间。因此,为评估模态阻尼比对谐响应结果的影响,需引入一种描述错频叶盘结构局部化程度的参数,即位移放大因子Ru=um/ut,其中ut、um分别为协调叶盘结构叶片和错频叶盘结构某叶片在频谱图上峰值对应的位移幅值。文献[4]、[5]认为,对于有N片叶片的错频叶盘结构,其位移放大因子的理论上限值为(1+N0.5)/2,而达到该上限值的条件是仅有一片叶片失调。对于本文的错频叶盘结构,应用上式可得位移放大因子的理论上限值为3.28。
以60%设计转速为例,以0.01 Hz作为扫频间隔,分别以0.01和0.001为各阶模态振型阻尼比进行谐响应计算,各叶片的最大位移放大因子如图6所示。可见,当阻尼较大时,会把各叶片的最大位移放大因子的差异相对抹平一些(即各叶片的位移放大因子更趋向平均),阻尼在错频叶盘系统中可起到抹平失调的作用。反之,阻尼较小时,错频叶盘结构局部化程度较高。

表1 不同扫掠频率和阻尼比下协调叶盘结构的谐响应结果Table 1 Harmonic response results of different swept-frequencies and damping ratios

图6 不同阻尼比下错频叶盘各叶片的最大位移放大因子Fig.6 Maximum displacement amplification factor of each blade on mistuned bladed disk with different damping ratios
3.3错频量对错频叶盘结构局部化程度的影响
首先定义错频叶盘结构中第i号叶片的错频量di=||fi′-fi/fi,其中fi和fi′分别为第i号叶片在错频前后的固有频率[6]。
为评价错频量对当前错频叶盘结构局部化程度的影响,维持当前错频叶盘结构在图2中的错频模式(即任取两个叶片i和j,令di/dj=常数),改变错频量进行谐响应分析。因此,假设当前错频叶盘结构中错频量最大叶片的编号为m,在每次改变错频量时,只要给定m号叶片的错频量,就可得到其它叶片的错频量。
仍以60%设计转速为例,给定扫频间隔为0.01 Hz,各阶模态振型阻尼比为0.001,分别给定不同错频叶盘结构最大错频量进行谐响应计算,各叶尖尾缘周向位移的谐响应频谱如图7所示。可见,错频量越大,频谱图上各叶片峰值出现的频率范围越分散,但各叶片峰值大小与错频量间并无明显关系。
图8给出了不同错频量对应的错频叶盘结构的最大位移放大因子。可见,错频量与最大位移放大因子之间并不存在简单的线性关系。当错频量在(0,0.01)范围内时,最大位移放大因子存在剧烈的突增突降,并在错频量为0.005时达到峰值;当错频量在(0.01,0.15)范围内时,最大位移放大因子变化较小。综合考虑降低错频叶盘结构局部化程度的需求和错频量的合理性,发现最大位移放大因子在区域内存在低点,所对应的错频量为0.04,是该错频模式下的较优错频量。
此外,错频叶盘结构最大位移放大因子出现的叶片号,也随错频量发生有规律变化,如表2所示。可见,随着错频量的增加,最大位移放大因子出现的叶片编号由15变为18,又变为28。

图7 不同错频量下错频叶盘结构的谐响应频谱图Fig.7 Harmonic response spectrogram of mistuned bladed disk with different mistuning magnitude
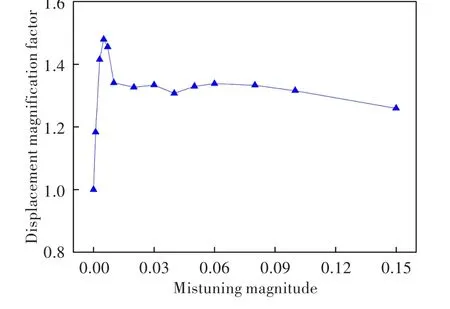
图8 不同错频量下错频叶盘结构的最大位移放大因子Fig.8 Maximum displacement amplification factor of mistuned bladed disk with different mistuning magnitude

表2 叶盘结构最大位移放大因子出现的叶片号Table 2 Blade index with maximum displacement amplification factor for bladed disk assembly
上述结果表明,在当前错频模式下,错频量与错频叶盘结构局部化程度之间并不存在简单的线性关系,最大位移放大因子出现的叶片号也不固定。因此,在错频叶盘结构设计中,需针对具体的错频模式,以提高气动弹性动稳定性和减小错频叶盘结构局部化为共同设计目标,寻找最优错频量。
3.4协调叶盘结构谐响应计算中转速的影响
一般的谐响应分析中,当计算每个扫掠频率时,都不考虑转速作用或施加固定转速。这样虽可减少计算量,但由于忽略了转动与激振力间的相互作用,可能会错估振动响应幅值。因此,本文试图在计算每个扫掠频率时,叶盘系统分别施加与Campbell图上共振点对应的转速。例如,若扫掠频率为230 Hz,计算采用的转速频率就是115 Hz,即转速为6 900 r/min,约为61.88%设计转速。由此得出,图3所给出的频率扫掠区间200~261 Hz,对应53.81%~70.22%设计转速范围。
给定各阶模态振型阻尼比为0.001,以0.1 Hz作为扫频间隔对协调叶盘结构进行谐响应计算,各叶尖尾缘周向位移频谱如图9所示。可见,最大谐响应位移幅值出现在236.4 Hz,此时对应63.61%设计转速。图9中也给出了固定转速(63.61%设计转速)下的位移频谱。由于在236.4 Hz处两种计算方法的转速相同,所以两者计算的峰值相同。但除了236.4 Hz外,可变转速计算的叶片在各个频率下对应的幅值,都比固定转速所计算的幅值高。

图9 协调叶盘结构叶片的谐响应频谱图Fig.9 Harmonic response spectrogram of tuned bladed disk
3.5错频叶盘结构谐响应计算中转速的影响
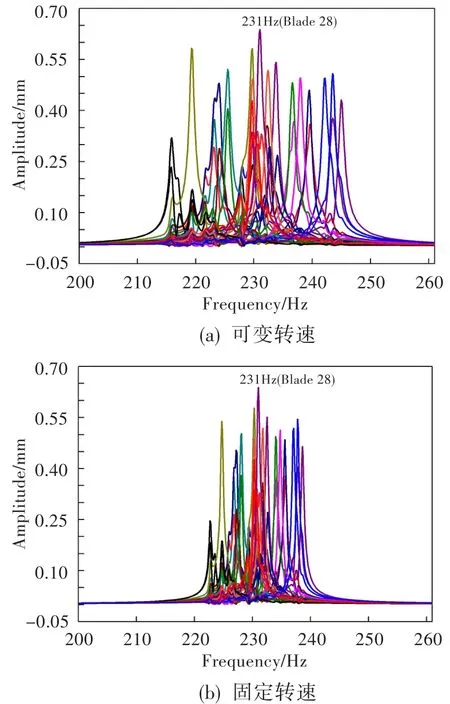
图10 错频叶盘结构各叶片的谐响应频谱Fig.10 Harmonic response spectrogram of mistuned bladed disk
给定各阶模态振型阻尼比为0.001,以0.1 Hz作为扫频间隔对错频叶盘结构进行谐响应计算,各叶尖尾缘周向位移频谱如图10(a)所示。可见,最大谐响应位移幅值出现在231.0 Hz,此时对应62.15%设计转速。与图10(b)中固定转速(62.15%设计转速)下的位移幅值图相比,由于在231.0 Hz处两种计算方法的转速相同,所以两者计算的峰值也相同。但可变转速计算的各个叶片位移峰值分散在更广阔的频率带内,且叶片位移峰值的均值及各叶片位移峰值的分布,与固定转速的计算结果也略有差别,其结果更能真实反映客观物理现象。
图11给出了可变和固定转速情况下各叶片的最大位移放大因子。可见,采用当前的错频方式和激励方式时,位移放大因子不超过1.374,该错频方案较为合理。
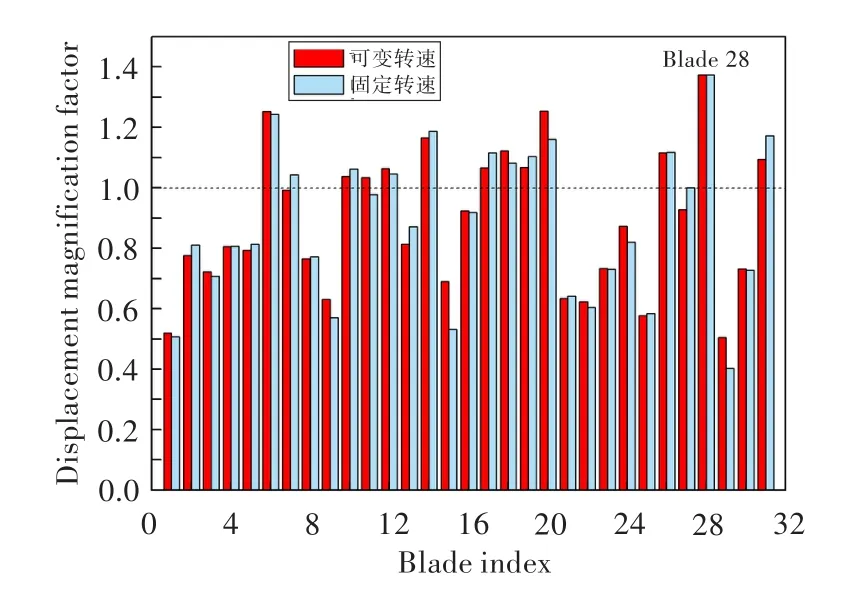
图11 错频叶盘结构各叶片的最大位移放大因子Fig.11 Maximum displacement amplification factor of each blade on mistuned bladed disk
4 气动弹性分析流程
根据上述结果,令各阶振型模态阻尼比为0.001,计算62.15%设计转速(错频叶盘结构2节径行波激励下最大位移所对应的转速)下2节径行波激励的强迫振动响应,分析整个错频叶盘结构的振幅和振动应力,并与63.61%设计转速(协调叶盘结构2节径行波激励下最大位移所对应转速)下2节径行激励的协调叶盘结构进行对比,以分析错频叶盘结构的振幅和应力放大情况。
图12为响应稳定后所有叶片的位移响应曲线,为清晰起见,各叶片位移曲线作了一定的平移。可见,错频叶盘结构出现了明显的振动局部化现象,28号叶片的振幅最大,这与图10(a)的谐响应计算结果一致。此外,各叶片间的相位角也不相同。
图13统计出了强迫振动响应和谐响应所计算的错频叶盘结构各叶片叶尖尾缘周向位移幅值的差别。可见,两种方法计算结果差别不大,最大仅为1.22%。差别可能源于计算误差、数值阻尼或强迫振动响应未计算至完全稳定。
图14给出了协调和错频叶盘结构的位移及振动应力分布云图。可见,协调叶盘结构的位移分布
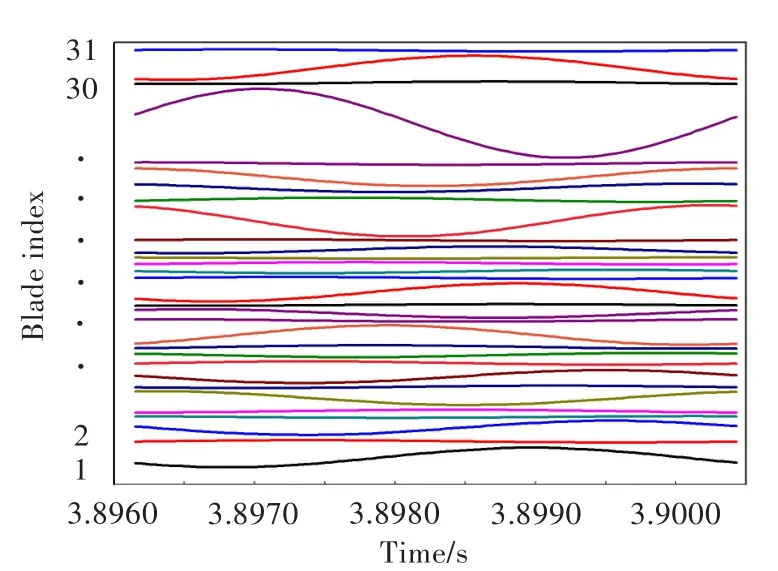
图12 错频叶盘结构所有叶片稳定后的响应曲线Fig.12 Response curves of all blades on mistuned bladed disk after stabilization
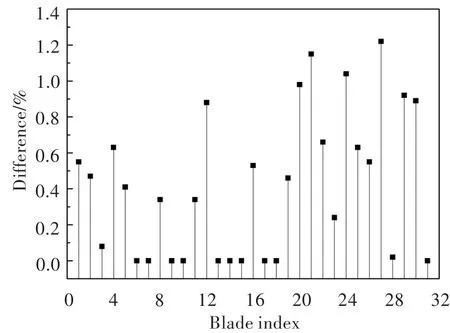
图13 强迫振动响应与谐响应计算所得位移幅值的差别Fig.13 Difference of displacement amplitude computed by force response and harmonic response analyses
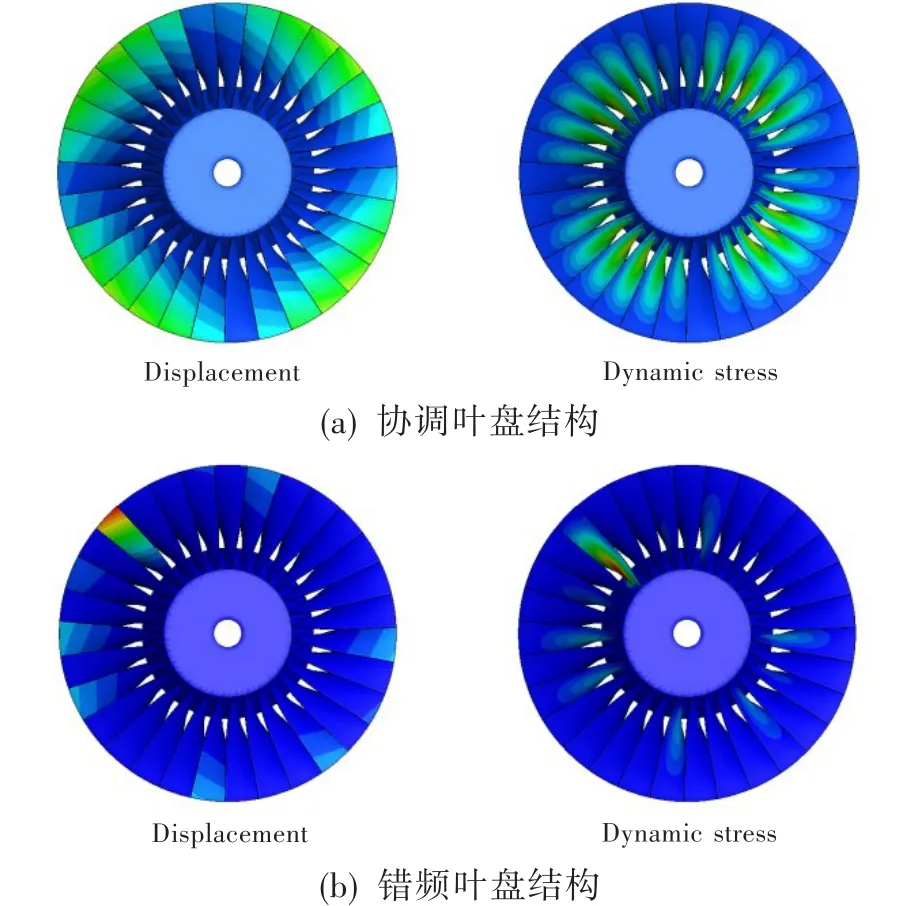
图14 协调和错频叶盘结构的位移和振动应力分布云图Fig.14 Displacement and dynamic stress contours of tuned and mistuned bladed disk
体现了2节径特征,而错频叶盘结构的位移分布失去了原协调叶盘结构的节径特征,其振动应力也出现了明显的局部化特性。
5 结论
(1)扫频间隔、阻尼比和错频量均对谐响应计算结果有一定影响。扫频间隔越小,计算精度越高,但计算时间也越长;阻尼越大,频谱图的峰值区域越平坦,对扫频间隔的敏感性越低;在本文参照试验所给出的错频模式下,错频叶盘结构局部化程度与错频量之间并不存在简单的线性关系,最大位移放大因子出现的叶片号也不固定。可见在错频叶盘结构设计中,需要针对具体的错频模式,以提高气动弹性动稳定性和减小错频叶盘结构局部化为设计目标,寻找最优错频量。
(2)相比固定转速计算结果,可变转速计算的各个叶片位移峰值分散在更广阔的频率带内,而且各叶片位移峰值的均值与固定转速的计算值也略有差别,更符合真实工况。
(3)谐响应和强迫振动响应计算获得的最大叶片振幅比较接近,因此,如果需要计算真实流场中气动力作用下错频叶盘结构的强迫振动响应,可先通过谐响应分析初步得出叶片的错频局部化特性,对不同的错频方案进行比较;然后在选定的错频方案下计算错频叶盘结构在流场中的强迫振动响应,获得该错频叶盘结构的振动特性。
(4)通过计算各叶片的位移放大因子,表明本文所采用的错频模式在2节径行波激励下较为合理。
[1]王建军,李其汉.航空发动机失谐叶盘振动减缩模型与应用[M].北京:国防工业出版社,2009.
[2]徐可宁,王延荣.时域法在压气机转子气动弹性计算中的应用[J].航空动力学报,2011,26(1):191—198.
[3]吴秋芳,杨士杰,段连丰.谐调与非谐调叶盘/盘失速颤振试验研究[R].1987.
[4]Whitehead D S.Effect of Mistuning on the Vibration of Turbomachine Blades Induced by Wakes[J].Journal of Me⁃chanical Engineering Science,1966,8(1):15—21.
[5]Whitehead D S.The Maximum Factor by Which Forced Vibration of Blades Can Increase due to Mistuning[J].Jour⁃nal of Engineering for Gas Turbines and Power,1998,120 (1):115—119.
[6]张锦,刘晓平.叶轮机振动模态分析理论及数值方法[M].北京:国防工业出版社,2001.
Vibration Response Analysis on Mistuned Bladed Disk Assembly of Compressor Rotors
XU Ke-ning1,WANG Yan-rong2,LIU Jin-long1
(1.China Aviation Engine Establishment,Beijing 100028,China;2.School of Power and Energy,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
The vibration response analysis has been performed for a mistuned bladed disk assembly using an aeroelastic analysis software AEAS,and the influence of different computational parameters and mistun⁃ing magnitude on the numerical simulation efficiency and accuracy were compared.The calculation results indicated that the transient displacement or dynamic stress response of mistuned bladed disk assembly can be obtained with harmonic response analysis and transient response analysis,and then the displacement am⁃plification factor of each blade can be calculated.The research on the influence of mistuning can be used to guide the design of mistuned bladed disk assembly,thus to minimize the risk of HCF failures caused by mis⁃tuning.
aero-engine;compressor rotor;mistuned blisk;harmonic response;forced response;finite element method
V231.92
A
1672-2620(2013)03-0006-06
2012-12-12;
2013-05-19
徐可宁(1980-),女,江苏徐州人,工程师,博士,主要从事航空发动机强度和振动研究。

