影响冷气掺混数值模拟精度的若干问题分析
何宏疆,綦蕾,王鹏,刘火星
影响冷气掺混数值模拟精度的若干问题分析
何宏疆,綦蕾,王鹏,刘火星
(北京航空航天大学能源与动力工程学院,航空发动机气动热力国家级重点实验室,北京100191)
对冷气掺混数值模拟中的计算网格、湍流模型、射流边界条件等影响精度的若干问题进行分析。在吹风比0.5下,对不同网格分布、湍流模型、射流边界条件进行数值模拟,所得结果与Ajersch的实验结果进行对比。结果表明,出口下游的网格分布可适当稀疏以减少计算量;在所研究的几种湍流模型中,k-ε模型所得结果与实验结果吻合得最好;考虑射流通道内流动能提高精度,在射流出口给定流场分布也可保证计算结果的精度。
航空发动机;气膜冷却;方孔射流;冷气掺混;数值模拟精度
numerical simulation precision
1 引言
随着航空发动机效率的提高,涡轮部件进口温度也不断提高。而涡轮部件进口温度的提高,直接威胁到发动机的安全性、可靠性和使用寿命。因此,探索成熟、高效的冷却方法日益重要。自上世纪70年代以来,气膜冷却因其良好的冷却效果被广泛应用于航空发动机涡轮部件。冷气掺混流动十分复杂,且有很强的三维特性,准确预测其特性有助于对冷气再附位置、入射深度做出判断。为此,很多学者对冷气掺混问题进行了大量实验和数值研究。
Zhou等[1,2]采用简化的涡轮叶片气膜冷却模型,对吹风比0.5、1.0、1.5三种情况进行了实验和数值模拟。结果表明,射流下游中线上的速度分布和雷诺应力分布相差较大,并认为采用的湍流模型均不能准确预测气膜冷却的流动特征。Hoda等[3]采用七种湍流模型来预测冷气掺混问题,表明所有模型均高估了射流下游尾迹区域内的速度。Hassan等[4]对比了k-ε、RNGk-ε、realizablek-ε、k-ω四种两方程湍流模型在解决冷气掺混问题上的效果,并分析了其局限性,认为标准k-ε模型得到的模拟效果最好。Keimasi等[5]采用雷诺平均方法研究了三维湍流垂直入射主流,分别采用了标准k-ε模型加壁面函数模型和SST模型,最终得到的平均速度分布与实验结果吻合得很好,但湍动能分布相差较大。Garg等[6]在文献中展示了射流入口边界条件对准确预测射流出口下游流动的重要性,表明不同射流入口边界条件可导致射流出口下游高达60%的换热系数差异。随着计算能力的提高,大涡模拟(LES)方法也被逐渐应用到对这一问题的研究中来。Guo等[7]采用LES方法,得到了比雷诺平均方法吻合更好的结果。刘斌[8]采用LES方法对方孔射流问题进行了模拟,其计算模型与Ajersch的实验模型相同,通过模拟吹风比1.5情况,加深了对各种涡结构发展过程的认识。
本文通过数值结果与实验结果的对比,来研究计算网格分布、湍流模型、边界条件等对冷气掺混数值模拟精度的影响。
2 计算域与边界条件
计算模型与Ajersch[2]的实验模型相同。实验中采用了6排垂直入射的方孔,本文选择一个周期作为计算域。实验研究了吹风比0.5、1.0和1.5三种情况,本文只针对吹风比0.5的情况。以实验测得参数作为边界条件,主流进口边界条件为给定速度分布、湍流度分布和总温。主流边界层内的速度和湍流度分布见图1,主流中各个方向的速度U=U∞=11 m/s,V=0,W=0,总温293.15 K。射流进口边界条件:射流进口湍流度为0.05,速度U=0,V=5.5 m/s,W=0,射流总温293.15 K。壁面两侧采用对称边界条件,壁面采用绝热无滑移壁面,出口给定大气压力,具体边界条件参见文献[1]、[2]。与图2的坐标系相对应,定义X方向为流向,Y方向为法向,Z方向为展向。取射流孔边长D为特征长度,且D=12.7 mm。主流流向长度为51D,法向长度为25D,展向宽度为3D。取射流孔中心为坐标原点,射流孔位置为X= -0.5D~0.5D,Z=-0.5D~0.5D,其入口位于Y=-5.0D处。主流入口位置为X=-10.5D,出口位于X=40.5D。

图1 主流进口边界层内的速度和湍流度分布Fig.1 Velocity and turbulence intensity distribution at mainstream inlet
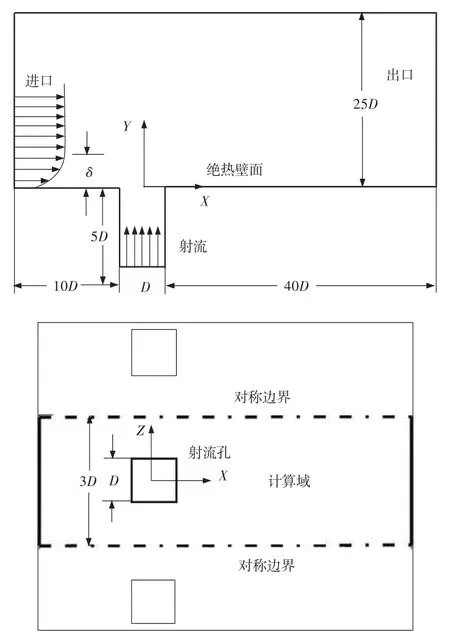
图2 计算域示意图Fig.2 Computational domain
3 结果分析
将数值结果与Ajersch等所做实验结果进行对比,包括流向速度、展向速度、法向速度、湍动能,且均以射流进口速度Vj进行无量纲化,距离以射流孔边长进行无量纲化。
3.1网格分布对数值模拟精度的影响
对表1中前四种网格分别进行计算。各种网格在射流孔内均匀分布,射流孔上、下游流向网格的膨胀比分别为1.12和1.06,法向膨胀比为1.06,射流孔中法向膨胀比为1.20,应用SST湍流模型。四种网格下射流出口(Z/D=0)位置法向速度对比如图3所示。可见,随着网格数目的增加,不同网格的射流孔出口法向速度的差异逐渐减小。其中第1种网格过高给出了射流孔上游的入射速度,但随着网格数目的增大,该位置的速度逐渐减小;网格3与网格4的结果相差很小。文献[1]中,在距射流出口较远的下游(X/D=3,5)位置,速度分量和湍动能与实验结果均相差很大。网格3在X/D=10位置的流向尺寸为0.48D,在主流出口为1.66D,网格过于稀疏可能是导致下游流场精度过低的原因。对网格3进行加密,其中主流进口至射流出口下游X/D=1.5位置的网格分布不变,X/D=1.5至主流出口的流向进行加密,主流通道中展向和法向的网格分布不变,网格数目由361 854增加为573 032,加密后的网格称为网格5。由图4可见,网格加密后,主流中X/D=10位置的网格尺寸由0.48D缩小为0.17D,主流出口附近最大网格尺寸由1.66D缩小为0.45D。射流通道内网格分布保持不变。但网格加密前后,出口下游各个位置的流向速度分量完全重合。下文中如无特殊说明,均以网格3作为计算网格。
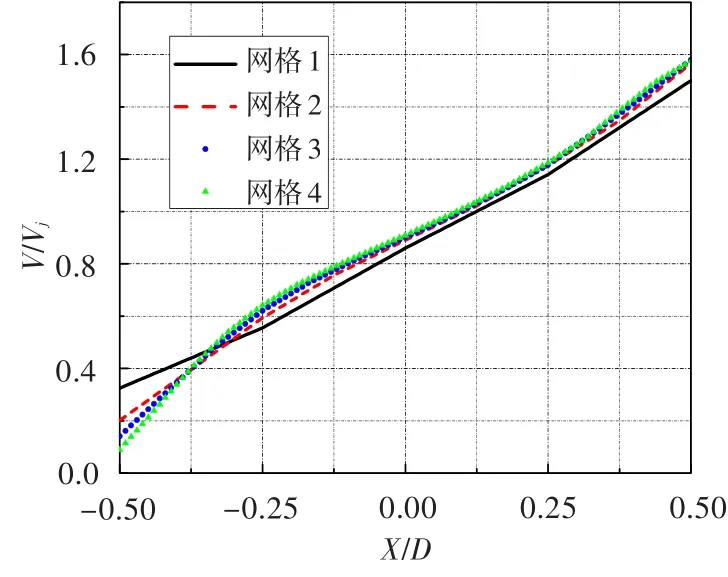
图3 射流出口中线法向速度对比Fig.3 Comparison of vertical velocity at the center line of jet exit

图4 网格3与网格5在Z/D=0位置上的流向速度对比Fig.4 Comparison of streamwise velocity forZ/D=0
3.2湍流模型对数值模拟精度的影响
对几种常用湍流模型(层流模型、零方程模型、四种两方程模型(k-ε、SST、k-ω、RNGk-ε)、Base⁃line湍流模型)进行验证。图5给出了射流孔中线不同流向位置(Z/D=0)的流向速度对比。在射流孔中心(X/D=0)位置,相对于其它湍流模型,层流模型在Y/D=0~0.5高度位置的流向速度偏小,而零方程模型在Y/D=0.5~2.0位置预测的流向速度偏小。这是由于零方程模型和层流模型只能给定速度分布与总温,不能给定进口湍流度,导致射流出口附近流场与实验偏差很大。两方程模型预测的射流孔出口处流向速度很接近,与实验结果也吻合得很好。在距射流出口下游1D位置,不同湍流模型预测的流向速度出现了明显差异。其中层流和零方程模型在壁面附近的趋势与实验结果相反,均在壁面附近向正流向运动;其它湍流模型在壁面附近的趋势与实验相同,均在壁面附近出现倒流。k-ε模型预测的倒流峰值低于其它湍流模型,SST、k-ω、RNGk-ε模型均给出了偏高的回流速度。随着X/D的增大,不同湍流模型之间的差异扩大。X/D=3位置,RNGk-ε模型得到的峰值为负数,而实验结果表明均为正向流动。RNGk-ε模型、零方程模型和层流模型加速偏离实验值,其中零方程预测速度严重偏离实验值,层流方程在X/D=5位置速度峰值仍是负值。k-ε、k-ω、SST湍流模型结果偏离实验值较小,但均偏低地预测了壁面附近的速度,k-ε模型结果与实验值最为接近。

表1 网格分布Table 1 Grid distribution
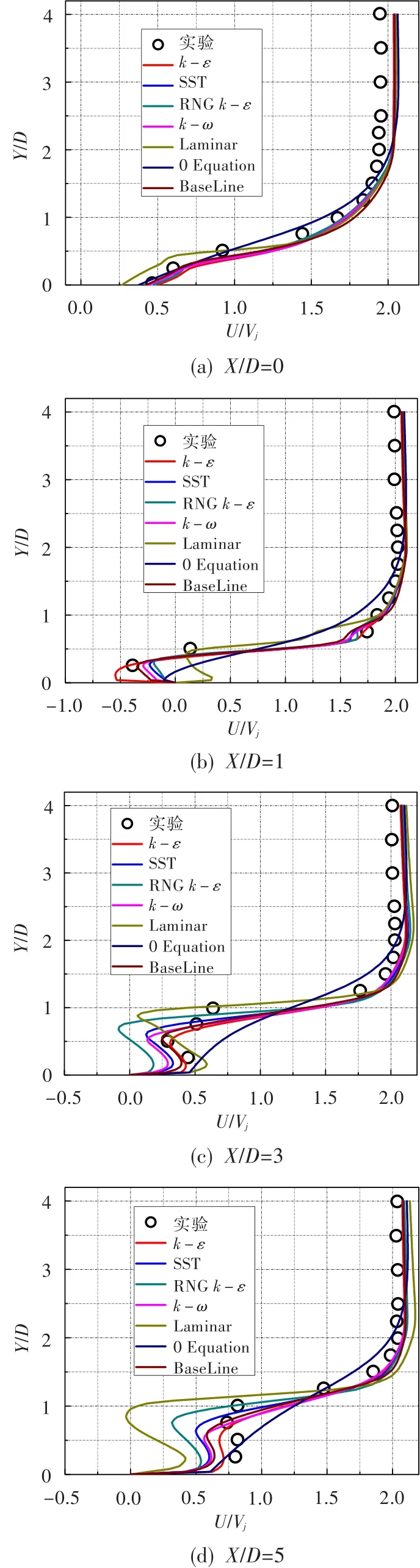
图5 不同湍流模型在Z/D=0位置上的流向速度对比Fig.5 Comparison between different turbulence models of streamwise velocity forZ/D=0
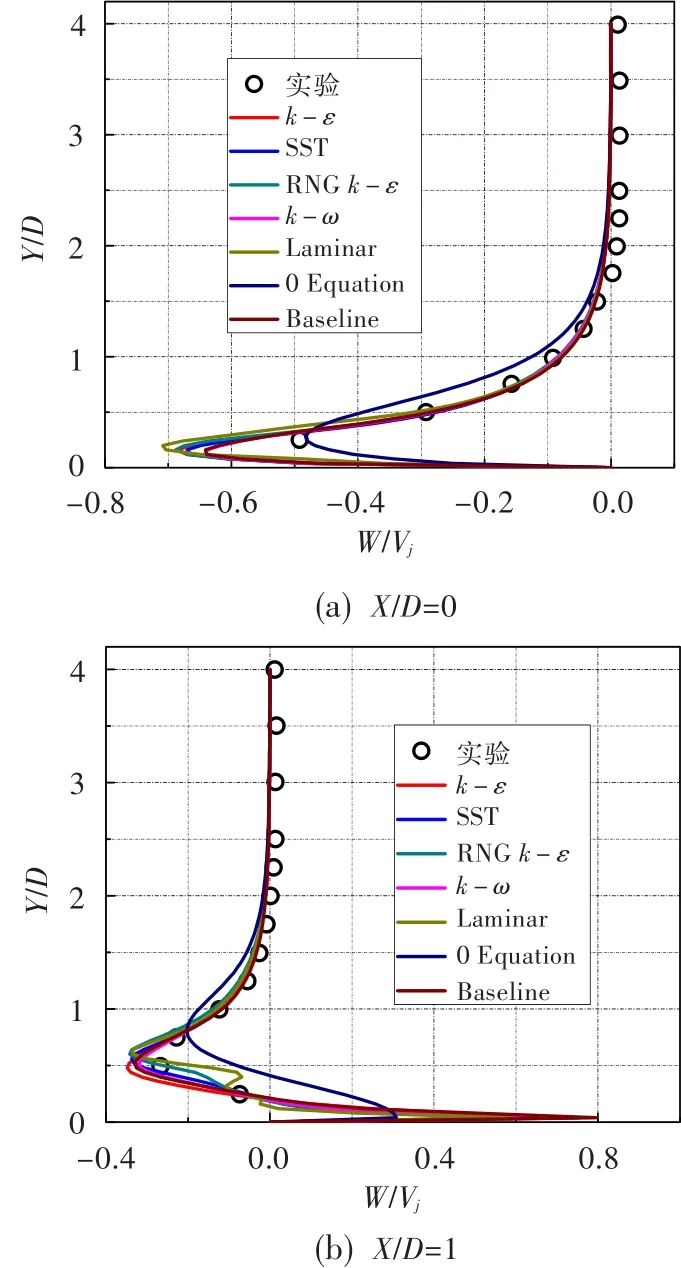
图6不同湍流模型在Z/D=-0.5位置上的展向速度对比Fig.6 Comparison between different turbulence models of cross-tunnel velocity forZ/D=-0.5
图6 给出了射流孔侧面边缘(Z/D=-0.5)不同湍流模型得到的展向速度与实验结果对比。在射流孔侧边(X/D=0)位置,各模型结果与实验结果的展向速度均为负值,表明流向均为远离射流孔方向,且展向速度在距壁面很短一段距离内就上升到峰值。零方程在射流出口就偏差实验值较远,其预测峰值为0.50Vj,其它模型则在0.65Vj~0.70Vj之间。在X/D=1位置,除零方程模型外,其余模型所得结果较为吻合,均预测到近壁面的正峰值和距壁面0.50D的负峰值。在壁面附近,对转涡受主流作用,展向速度为正值,朝射流孔流动;在对转涡上半区,展向速度为负,远离射流孔流动。两个峰值的位置表明了对转涡的范围,而实验结果并没有表现出近壁面峰值的存在,计算的对转涡区域与实验结果吻合较好。随着距射流出口距离的增加,对转涡强度逐渐减小,各数值结果与实验结果的偏差增大。
图7给出了Z/D=-1位置上的法向速度分布。在X/D=0位置,零方程模型和层流模型均在壁面附近得到了负值,即指向壁面流动,该位置为对转涡侧边缘;实验结果表明法向速度为正值,其流向为远离壁面方向,其它两方程模型均与实验结果吻合得很好。在X/D=1位置,壁面附近法向速度出现低峰值,对应对转涡外侧向下流动;在距壁面1D位置则出现正峰值,为主流在对转涡位置以上加速,两个峰值所在高度与图6的一致。随着流体向下游流动,展向速度变小,对转涡强度逐渐减弱,两方程湍流模型预测趋势相同,RNGk-ε模型预测的低峰值过低,k-ε模型和k-ω模型与实验结果吻合得很好。
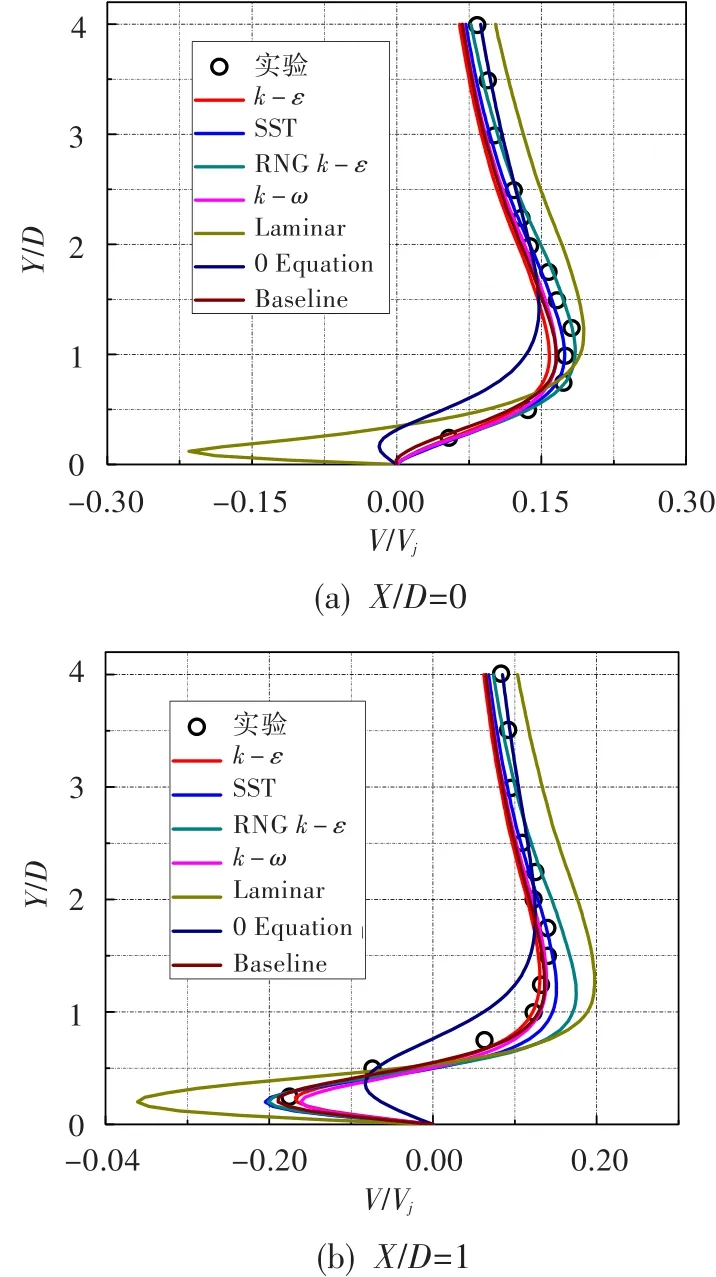
图7不同湍流模型在Z/D=-1位置上的法向速度对比Fig.7 Comparison between different turbulence models of vertical velocity for Z/D=-1
图8 给出了射流出口中线(Z/D=0)位置上的湍动能(k/Vj)分布。在射流出口位置,层流模型高估了主流的湍动能,其它模型均低估了湍动能的峰值,这与流向速度沿法向的速度梯度(∂U/∂Y)相关。在距射流出口1D位置,各模型均得到了三个峰值,分别对应壁面射流、射流尾迹和剪切层流动,这些位置的∂U/∂Y较大,k-ε模型高估了峰值,SST、RNGk-ε模型低估了峰值,k-ω模型与实验结果吻合较好。随着流体向下游流动,湍动能峰值减小,但峰值所在高度提高。文献[5]认为,数值结果的不准确与射流孔出口流场有关,在Ajersch的实验中,射流气体由储气室进入射流通道时,会在锐角处加速,从而导致射流进口气体湍动能不均匀。因此在下文研究中,将采用实验得到的射流通道出口截面参数作为数值模拟的射流边界条件,从而对射流边界条件的影响进行讨论。综上,相对于其它湍流模型,k-ε模型能较为准确地预测各速度分量和湍动能分布。

图8 不同湍流模型在Z/D=0位置上的湍动能对比Fig.8 Comparison between different turbulence models of turbulence kinetic energy for Z/D=0
3.3射流边界条件的影响
对两种射流边界条件进行计算:仅把射流进口位置参数作为射流出口边界条件(CASE2),和以实验测得的射流出口速度分布、平均湍动能作为射流边界条件(CASE3)。所采用的计算域不包括射流通道,并将结果与考虑射流通道的计算结果、实验结果进行对比。计算网格均采用网格3,湍流模型为k-ε模型。
图9给出了射流出口位置法向速度(V/Vj)分布。在射流孔迎风侧至背风侧,法向速度均在0.2Vj~1.7 Vj之间,表明实验结果作为射流出口位置边界条件可行。
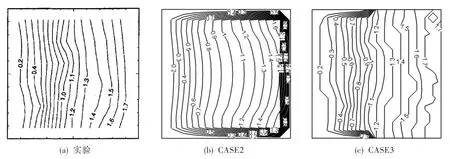
图9 射流出口位置法向速度分布Fig.9 Vertical velocity distribution at jet exit
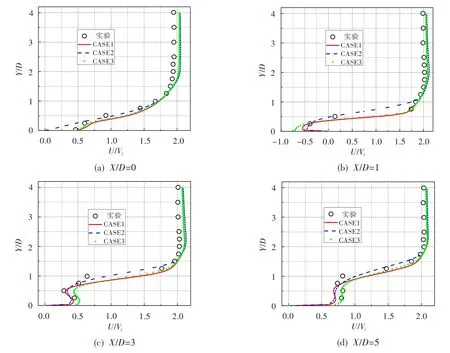
图10 不同射流边界条件在Z=0位置上的流向速度对比Fig.10 Comparison between different jet conditions of streamwise velocity for Z/D=0
图10 给出了Z/D=0位置上的流向速度对比,CASE1结果为考虑射流通道时的计算结果。在射流孔出口中心,CASE2的进口流向速度分量为零,CASE1中射流在冷气通道内受主流挤压而产生流向分量,在射流出口流向速度约为0.5Vj,CASE1、CASE3的分布与实验结果吻合得很好。在X/D=1位置,实验、CASE1、CASE3结果几乎重合,由于CASE2的射流出口流向速度分布与实验偏差较大,在X/D=1位置尾迹区的速度要低于实验值。在壁面到0.25D高度内,CASE3的低峰值比CASE1的小,说明采用实验结果作为边界条件下,在距射流出口很短一段距离内的倒流加强。在下游发展过程中,CASE3在壁面附近的流向速度加速明显,在X/D=3位置,CASE3尾迹区的流向速度已高于考虑射流通道的流向速度。在距射流出口较长位置上,CASE1和CASE2的结果与实验结果的偏差逐渐扩大。然而在壁面附近,采用实验结果作为进口边界条件所得流速与实验结果最为接近,CASE1与CASE2所得的流向速度均偏小。在X/D=3~5范围内,CASE2结果在距壁面1D高度内的速度分布较实验结果偏低。
图11给出了方孔两侧(Z/D=-0.5)位置上的展向速度对比。在X/D=0位置,展向速度与实验结果吻合较好,采用射流出口测量值为边界条件后,在0.2D高度处的展向速度峰值为0.8Vj,高于考虑射流通道算例中的0.7Vj。对比X/D=0与X/D=1流向位置,所测低峰值绝对值由0.5Vj减小为0.3Vj,而峰值所在高度由0.2D升至0.5D。在X/D=1位置,壁面附近的正峰值高达0.6Vj,CASE1与CASE3在Y/D=0.5高度存在负峰值,CASE2所预测的负峰值位于偏高的Y/D=0.8位置,高估了对转涡对的范围。
图12给出了Z/D=-1位置上的法向速度分布。对比CASE2、CASE3,虽然均不考虑射流通道,但CASE2在X/D=0位置得到的低峰值为负值,在靠近壁面有向下的流动,说明在射流出口对转涡已形成,这与实验结果不符;受射流挤压,主流沿法向加速至0.15Vj。相对于CASE2,CASE3与实验结果吻合得更好,但在主流区,CASE2、CASE3均低于实验结果,表明射流出口速度分布对对转涡的形成至关重要。在X/D=1位置,由前文分析已知,该位置位于对转涡边缘,其法向速度方向指向壁面,在对转涡位置以上,主流向上绕过对转涡加速流动,法向速度迅速增加,在距壁面4D范围内,加速后大于0.05Vj。对比考虑射流通道结果,CASE2的正峰值所在高度最高。

图11 不同射流边界条件在Z/D=-0.5位置上的展向速度对比Fig.11 Comparison between different jet conditions of cross-tunnel velocity for Z/D=-0.5

图12 不同射流边界条件在Z=-1D位置上的法向速度对比Fig.12 Comparison between different jet conditions of vertical velocity for Z/D=-1
图13 为不同射流边界条件得到的湍动能对比。在射流孔出口位置,CASE2与CASE3预测的湍动能峰值大小接近,但CASE2预测峰值位置偏高,CASE3所得高度与实验值吻合较好。在下游位置,各数值结果均与实验结果吻合不好,在X/D=1位置,CASE2的湍动能比CASE1的低,这是由于主流与射流在射流通道内已开始相互作用,湍动能会在射流通道内部提高,在射流孔下游表现明显,不考虑射流通道就不能对通道内的流动进行预测,湍动能偏低;湍动能与尾迹区内的流向速度梯度相关,所以CASE3的湍动能偏大。
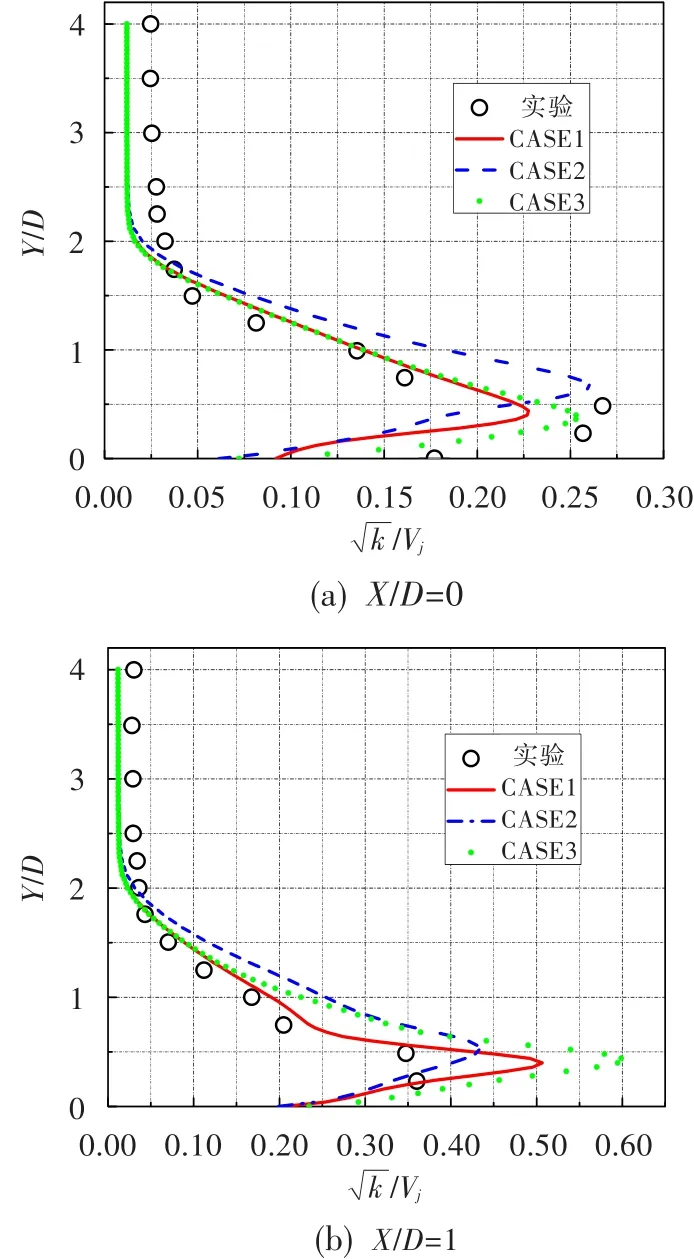
图13 不同射流边界条件在Z=0位置上的湍动能对比Fig.13 Comparison between different jet conditions of turbulence kinetic energy for Z/D=0
4 结论
(1)在射流出口远下游,各数值结果与实验结果偏差均较大,加密下游网格,所得流向速度分布保持不变。射流孔下游网格分布可适当稀疏,有利于减少总体网格数目,从而减少计算量。
(2)解决冷气掺混问题的常用湍流模型中,两方程模型普遍比层流方程模型和零方程模型表现好。相对于其它湍流模型,k-ε模型结果与实验值吻合最好,SST、k-ω、RNGk-ε模型均给出了偏高的回流速度;在距射流孔较远的流向位置,所采用的湍流模型均高估了对转涡强度;k-ε模型能较为准确地预测射流与主流相互作用产生的射流尾迹、对转涡等流动特征。
(3)在气膜冷却数值研究中,应考虑射流通道,对射流通道内流动进行模拟,有助于得到准确的射流出口流场,从而得到冷气覆盖范围、冷却效果等参数。在冷却通道未知的情况下,根据经验在射流出口给定速度分布和湍流度作为射流的边界条件,也有助于提高气膜冷却问题数值模拟精度。
[1]Zhou J M.A Computational and Experimental Investiga⁃tion of Gas Turbine Blade Film Cooling[D].Vancouver:University of British Columbia,1994.
[2]Ajersch P,Ketler S,Zhou J M,et al.Multiple Jets in a Cross-Flow:Detailed Measurements and Numerical Simu⁃lations[J].ASME Journal of Turbomachinery,1997,119:330—342.
[3]Hoda A,Acharya S.Predictions of a Film Coolant Jet in Cross-Flow with Different Turbulence Models[J].ASME Journal of Turbomachinery,2000,122:558—569.
[4]Hassan J S,Yavuzkurt S.Comparison of Four Different Two-Equation Models of Turbulence in Predicting Film Cooling Performance[R].ASME GT2006-90860,2006.
[5]Keimasi M R,Taeibi-Rahni M.Numerical Simulation of Jets in a Cross-Flow Using Different Turbulence Models [J].AIAA J,2001,39:2268—2277.
[6]Garg V K,Gaugler R E.Effect of Velocity and Tempera⁃ture Distribution at the Hole Exit on Film Cooling of Tur⁃bine Blades[R].ASME 95-GT-2,1995.
[7]Guo X,Schröder W.Large Eddy Simulation of Film Cool⁃ing Flows[J].Comput.Fluids,2006,35:587—606.
[8]刘斌,任丽芸,叶建,等.方孔横向射流的大涡模拟研究[J].航空科学技术,2009,(2):40—43.
Parameters Affecting Numerical Simulation Precision for Cooling Air Mixing
HE Hong-jiang,QI Lei,WANG Peng,LIU Huo-xing,ZOU Zheng-ping
(National Key Laboratory of Science and Technology on Aero-Engine Aero-Thermodynamics,School of Energy and Power Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Several parameters which affect the precision of numerical simulation for cooling air mixing were investigated,including mesh,turbulence model and boundary conditions.The comparison between the results with these parameters and measurement at a blowing ratio of 0.5 was made.The meshs at the far downstream from the exit of injection could be coarser to reduce the amount of computation.Thek-εturbu⁃lence model produced the result which matched the measurement best.The distribution of velocity and tur⁃bulence kinetic energy at the exit of injection is non-uniform because of the flow within the jet channel,so the geometry of jet channel should be taken into consideration to elevate the precision of numerical simula⁃tion.Also,distribution of flow-field at the jet exit could be fixed to ensure the precision of computation.
aero-engine;film cooling;square jet in cross-flow;cooling air in cross-flow;
V231.3
A
1672-2620(2013)03-00 21-08
2012-09-10;
2013-03-26
武器装备预研基金(9140C410101110C4101),国家自然科学基金(51106004)
何宏疆(1987-),男,新疆昌吉人,硕士研究生,主要从事叶轮机内部流动机理研究。

