尾迹诱导下低压涡轮边界层转捩的数值模拟

向欢，杨荣菲，葛宁

尾迹诱导下低压涡轮边界层转捩的数值模拟

向欢，杨荣菲，葛宁

(南京航空航天大学能源与动力学院，江苏南京210016)

为研究尾迹诱导下低压涡轮的边界层发展，采用基于三阶MUSCL-Roe格式、引入转捩准则后的一方程Spalart&Allmaras模型和隐式牛顿迭代时间推进的非定常雷诺平均计算方法，对上游运动圆柱产生的周期性尾迹作用下的T106低压涡轮叶片边界层转捩流动进行了数值模拟。定常来流下，准确捕捉到分离诱导转捩及雷诺数效应现象；尾迹作用下的非定常计算，则揭示了尾迹在叶栅通道内的输运过程，及尾迹对低压涡轮吸力面上层流分离的抑制作用。

T106低压涡轮叶片；上游运动圆柱；非定常尾迹；边界层转捩；雷诺数效应

Reynolds number effects

1 引言

现代低压涡轮设计往往追求更高的载荷和效率，但其工作雷诺数随飞机工作状态的不同而剧烈变化。尤其是在高空巡航状态，低压涡轮工作在低雷诺数环境中，叶片吸力面边界层变厚且极易分离，可能造成较大损失，导致涡轮效率急剧下降、耗油率增大。然而，此时的分离过程具有很强的非定常性，且易受上游叶排尾迹、进口湍流度及雷诺数变化等因素影响。因此，在低压涡轮设计中，合理利用以上因素改善其在巡航状态下的性能显得极其重要。其中，合理利用上游叶片尾迹与下游叶片边界层间的相互作用，能有效抑制下游叶片吸力面边界层的分离，改善涡轮级性能，且不会增加发动机复杂性，易于工程实现，从而引起国内外学者的广泛关注。

Hodson等[1～4]对非定常尾迹诱导低压涡轮边界层分离和转捩进行了深入研究，分析了尾迹在叶栅通道内的输运过程、尾迹的负射流作用及尾迹通过不同模式诱导边界层转捩的机理等。Halstead等[5]分析、总结了非定常尾迹对压气机/涡轮表面边界层发展的影响，认为尾迹作用下压气机/涡轮叶片吸力面上存在较大的转捩区，尾迹诱导产生的沉寂区内速度型较为饱满，能使分离点后移，减小分离泡长度并推迟转捩点位置。此外，非定常尾迹对边界层发展的影响，与雷诺数、叶片负荷、尾迹频率、尾迹湍流度及时序效应等因素有关。邹正平等[6～8]对低压涡轮环境中尾迹与边界层的相互作用进行了数值模拟和试验研究，也取得了很好的研究成果。

本文通过圆柱尾迹诱导T106低压涡轮叶片边界层转捩的流动算例，对比已有研究结果，来验证课题组自行开发的CFD软件NUAA-Turbo在压气机/涡轮动-静叶相互干扰中的适用性。

2 求解器描述

2.1控制方程及数值解法

采用课题组自行开发的基于结构化网格的CFD软件NUAA-Turbo进行计算。该软件适用于绝对坐标系下叶轮机内的非定常流场计算，计算采用的绕X轴等Ω转速旋转的曲线坐标系下绝对速度的三维可压缩非定常N-S方程为：

式中：Q为守恒变量，F、G、H为无粘对流通量，Fd、Gd、Hd为粘性扩散通量，S为考虑哥氏力和离心力的源项，具体表达形式及各项的物理意义见文献[9]。

采用有限体积法数值求解方程，其中无粘对流通量、粘性扩散通量分别采取隐式算法和显式算法求解。无粘对流通量计算采用Roe格式，并运用具有二阶/三阶空间精度van Leer的MUSCL插值方法，粘性扩散通量则采用二阶中心差分格式计算。时间推进方面，采用牛顿迭代法隐式求解关于守恒变量的非线性方程组，对流通量的线化应用Roe近似雅可比矩阵，并采用多步对称高斯塞德尔方法求出牛顿线化后方程组的渐近解。定常隐式计算采用具有一阶时间精度的后差格式，非定常隐式计算采用具有二阶时间精度的Jameson双时间步法[10]，且都采用当地时间步长方法加速解收敛。边界条件依据特征波理论给定。

2.2湍流-转捩模型

粘性扩散通量中的湍流粘性系数，采用Eulitz[11，12]提出的引入转捩准则后的一方程Spalart&Allma⁃ras(SA)模型进行计算，故NUAA-Turbo能同时计算转捩和湍流流动。对原始SA模型方程中的生成项进行输运，并引进一套转捩判据实现对转捩的预测。此外，为考虑自由流湍流度的影响，还额外加入了一项生成项。修改后的SA模型方程为：

式中：方程右端各项依次为生成项、耗散项、扩散项和自由流湍流度生成项。其中生成项中的PvT为额外引进的输运变量，其输运方程为：

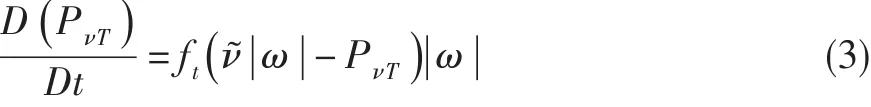
转捩的判断根据Drela[13]提出的转捩准则进行，模型中各项的物理意义及各常数值参见文献[12]。运用此模型时，采用基于Baldwin-Lomax模型的BL函数法计算边界层厚度[14]，然后求出位移厚度、动量厚度和形状因子等边界层参数。湍流模型扩散项中的偏导数项采取中心差分计算，生成项和耗散项则直接采用网格单元中心值。此外，湍流模型方程和生成项输运方程的离散方法与N-S方程的类似。

3 计算结果及分析

3.1算例说明

采用文献[15]中通过安装在皮带上绕叶片运动的圆柱产生尾迹，由此诱导下游叶片边界层非定常转捩的方法，研究非定常尾迹诱导边界层转捩流动。计算采用的T106A低压涡轮，叶栅稠度为0.799，进气角为37.7°，详细参数参见文献[16]。圆柱直径为2 mm，移动速度为40 m/s，圆柱间距与叶栅栅距相同(即圆柱与叶片数目比为1:1)，圆柱中心与叶片前缘的轴向距离为1倍叶片轴向弦长。共计算了两种不同雷诺数下无上游尾迹作用时的定常来流情形，及低雷诺数下受上游尾迹作用时的非定常来流情形。计算条件如表1所示，其中雷诺数Re2th基于叶片弦长及出口等熵流动参数，Re0基于叶片弦长及进口流动总参数，p0为进口总压，p2为出口静压。进、出口马赫数分别为0.21和0.40，进口总温T0=313 K，进口湍流度Tu1=1.5%。

表1 计算条件Table 1 Computational conditions

网格生成采用课题组自行开发的多块结构化网格生成程序。图1为本文非定常来流情形计算时采用的单通道网格，计算域包括运动圆柱和静止叶栅通道两部分。为较好把握边界层内流动，圆柱和叶片表面均采用O型网格，网格点数分别为99×50和600×45，离壁第一点保证在y+＜1范围内；主流区采用H型网格。移动网格块与静止网格块间的交界面处布置100个等间距网格点，上游圆柱网格移动过程中交接面两侧分别按交界体积进行加权平均，然后用作相应块的虚拟网格单元。整个单通道计算域内的总网格节点数为76 005。

图1 计算网格Fig.1 Computational grids

3.2无上游尾迹作用时的定常来流情形

为研究低压涡轮的雷诺数效应，首先计算了高、低两种雷诺数下不受上游圆柱尾迹干扰时的定常来流情形。不同雷诺数下，叶片表面压力分布的计算值与实验值[11，12]的对比如图2所示，可见二者吻合得非常好，只在图中右上方放大图所示的吸力面尾缘附近有所区别(此处的压力对层流分离和转捩十分敏感)。低雷诺数工况下，吸力面后半部压力逐渐上升，并在x/L=0.88位置后趋于平缓，表明此处边界层发生了层流分离；然后在x/L=0.92位置处的分离自由剪切层中发生转捩，转捩点后压力迅速增大，最终达到尾缘压力值。而高雷诺数工况下，转捩起始点提前到分离点之前，导致层流分离泡不能完全发展。

图3展示了两种雷诺数下壁面摩擦系数和吸力面边界层形状因子的变化情况。其中，壁面摩擦系数为负、层流边界层形状因子大于4，表明边界层发生分离。与压力分布的分析一样，低雷诺数下的层流分离泡比高雷诺数下的更大。而转捩起始点位置可根据壁面摩擦系数的急增来判断，高雷诺数下转捩发生得更早，因而起始点位置更靠近上游。此外，Eulitz[11]指出，对于形状因子为2.59的层流平板边界层，壁面摩擦系数与雷诺数的平方根呈反比。图3中吸力面前60%弦长范围内边界层形状因子接近2.6，对应的壁面摩擦系数分布也恰当反映了此雷诺数效应。图4列出了两种雷诺数下吸力面尾缘附近的速度矢量和无量纲涡粘性系数分布，可见低雷诺数下吸力面尾缘处存在一个较大的分离泡，而高雷诺数下的转捩起始点比低雷诺数下的更为靠前。

图2 无上游尾迹作用时叶片表面的压力分布Fig.2 Comparison of predicted and measured surface pressure distributions

3.3受上游尾迹作用时的非定常来流情形

以定常来流结果作为非定常计算的初始流场。Hodson[3，4]认为，尾迹实质是一种负射流，在叶栅通道内的输运过程大致为：尾迹在叶片前缘平面附近被叶片前缘切割成两段；叶栅通道内的流速比叶片前缘位置处的大很多，以当地流速进行输运的尾迹因而弯曲成弓形；尾迹进入叶栅通道内，在靠吸力面一侧大幅加速，在靠压力面一侧减速而相对靠后，于是压力面一侧的尾迹轴线沿逆时针方向缓慢旋转，最终几乎与压力面平行，即尾迹的再定向过程。图5为本文非定常来流情形下某一瞬时的扰动速度矢量图，图中红线标出了尾迹的外形。从图中看，尾迹呈弓形，受拉伸作用压力面附近尾迹变长、变细，而吸力面弓形顶点附近尾迹变粗，且尾迹内流体速度由压力面指向吸力面，形成漩涡(蓝色圆圈所示)。

图3 边界层参数与Eulitz计算结果[11，12]的对比Fig.3 Comparison of predicted boundary layer parameters and Eulitz′s results

图4不同雷诺数下的速度矢量及涡粘性系数分布Fig.4 Velocity vectors and eddy-viscosity distribution for different Reynolds numbers

图6 给出了一个尾迹传播周期内四等分时刻下，瞬时涡粘性系数等值线、涡量等值线、壁面摩擦系数分布及尾缘附近涡粘性系数等值线，图中T表示转捩起始点。从涡粘性系数和涡量分布中可看到，圆柱和叶片的尾迹中均出现了卡门涡街，伴随着两条涡量分支(蓝色为负，即逆时针；红/橙色为正，即顺时针)，也可清晰看出前述尾迹在叶栅通道内的输运过程。从壁面摩擦系数分布中可看到，吸力面一侧受尾迹与边界层的相互作用，层流区和转捩区内的壁面摩擦系数均出现了大幅扰动。t=t0时刻，尾迹尚未到达吸力面尾缘，转捩发生在较为靠后的x/L=0.92位置，转捩点后壁面摩擦系数增大；t= t0+T/4时刻，尾迹撞击到吸力面尾缘附近，相对于前一时刻转捩起始点位置有所提前；t=t0+2T/4时刻，尾迹尾部到达吸力面尾缘附近，此时转捩起始点移动到最为靠前的x/L≈0.75位置，转捩点后尾迹的撞击又使得较高的壁面摩擦系数减小；t=t0+3T/4时刻，尾迹已完全通过叶栅通道到达尾缘下游，而下一尾迹尚未到来，此时壁面摩擦系数出现两个波谷，即尾缘处存在两个转捩区。前转捩区尾部受沉寂效应影响[11]而再层流化，涡粘性系数减弱，此后层流边界层受尾缘处扰动影响而再次发生转捩，形成第二个转捩区。

相比定常来流情形，非定常来流情形下各时刻吸力面壁面摩擦系数均为正值，即层流分离泡并未出现，表明此时上游圆柱产生的非定常尾迹，能有效抑制低压涡轮叶片吸力面尾缘处的层流分离。

图5 瞬时扰动速度矢量图Fig.5 Instantaneous distributions of perturbation velocity vectors

4 结论

(1)无上游尾迹作用时的定常来流情形，叶片表面压力分布的计算值与实验值非常吻合，边界层参数也与Eulitz的计算结果吻合良好，且准确模拟了分离诱导转捩和雷诺数效应现象。

图6 尾迹干扰下的流场演化过程Fig.6 Temporal evolution of wake-disturbed flow

(2)受上游尾迹作用时的非定常来流情形，计算结果清晰地展示了尾迹在叶栅通道内的输运过程及尾迹的负射流作用，揭示了上游尾迹对低压涡轮边界层发展的影响，及周期性尾迹对层流分离泡的抑制作用。

(3)本文所采用的湍流-转捩模型，对尾迹诱导下叶片边界层转捩流动有较强的预测能力，初步验证了NUAA-Turbo软件在压气机/涡轮动-静叶相互干扰问题中的适用性。

[1]Hodson H P，Howell R J.The Role of Transition in High-Lift Low-Pressure Turbines for Aeroengines[J]. Progress in Aerospace Science，2005，41：419—454.

[2]Hodson H P，Howell R J.Bladerow Interactions,Transi⁃tion,and High-Lift Aerofoils in Low-Pressure Turbines [J].Annu.Rev.Fluid Mech.，2005，37：71—98.

[3]Stieger R D，Hodson H P.The Unsteady Development of a Turbulent Wake through a Downstream Low-Pressure Tur⁃bine Blade Passage[J].ASME Journal of Turbomachinery，2005，127：388—394.

[4]Stieger R D，Hodson H P.The Transition Mechanism of Highly-LoadedLPTurbineBlades[R].ASME GT2003-38304，2003.

[5]Halstead D E，Wisler D C，Okiishi T H，et al.Bound⁃ary-Layer Development in Axial Compressors and Tur⁃bines:Part 1 of 4-Composite Picture[J].ASME Journal of Turbomachinery，1997，119：114—127.

[6]叶建，邹正平.低雷诺数下周期性尾迹/层流分离泡相互作用的大涡模拟[J].工程热物理学报，2007，28(2)：215—218.

[7]杨琳，邹正平，李维.低雷诺数下尾迹与分离边界层的相互作用研究[J].航空学报，2007，28(1)：58—63.

[8]张伟昊，刘火星，李维，等.尾迹与涡轮叶栅边界层的相互作用[J].航空动力学报，2009，24(4)：843—850.

[9]Chen J P.Unsteady Three-Dimensional Thin-Layer Navi⁃er-Stokes Solutions for Turbomachinery in Transonic flow [D].Mississippi：Mississippi State University，1991.

[10]Jameson A.Time Dependent Calculations Using Multigrid with Application to Unsteady Flows Past Airfoils and Wings[R].AIAA 91-1596，1991.

[11]Eulitz F.A RANS Method for the Time-Accurate Simula⁃tion of Wake Induced Boundary-Layer Transition in Tur⁃bine Flows[R].AD-A373311,1999.

[12]Eulitz F.Numerische Simulation und Modellierung der In⁃ stationären Strömung in Turbomaschinen[D].Ruhr-Uni⁃versität Bochum，DLR-Forschungsbericht，2000.

[13]Drela M.MISES Implementation of Modified Abu-Ghan⁃nam/Shaw Criterion[R].MIT Aero-Astro，1995.

[14]杨琳，邹正平，宁方飞，等.边界层转捩的数值模拟[J].航空动力学报，2005，20(3)：355—360.

[15]Acton P，Fottner L.Investigation of the Boundary Layer Development on a Highly Loaded Low Pressure Turbine Cascade under the Influence of Instationary Inlet Flow Conditions[C]//.Proceedings of 8th ISUAAT.Stockholm，1997.

[16]Stieger R D.The Effects of Wakes on Separating Boundary Layers in Low Pressure Turbines[D].Cambridge：Cam⁃bridge University，2002.

Numerical Simulation of Wake-Induced Boundary Layer Transition in Low-Pressure Turbine

XIANG Huan，YANG Rong-fei，GE Ning
(College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

In order to study the wake-induced boundary layer transition in low-pressure turbine,the un⁃steady Reynolds-averaged Navier-Stokes(RANS)method was adopted to simulate the boundary layer tran⁃sition flow of the T106 low-pressure turbine blade which was subjected to the periodical wake of the up⁃stream moving bar.The RANS code included third order MUSCL-Roe scheme,the Spalart&Allmaras tur⁃bulence model combined with a transition correlation,and Newton iterative method for implicit time ad⁃vancement.In the steady case without any wake disturbance,the laminar separation bubble induced transi⁃tion and the Reynolds number effects were correctly predicted.While in the disturbed case,the convection of wake through a turbine cascade was presented and the laminar separation on the suction side was inhibit⁃ed by the wake of upstream moving bar.

T106 LP turbine blade；upstream moving bar；unsteady wake；boundary-layer transition；

V231.3

A

1672-2620(2013)03-0029-05

2012-08-06；

2013-05-30

向欢(1987-)，男，重庆南川人，硕士研究生，主要从事叶轮机气动力学研究。