失谐叶盘系统避共振可靠度评估方法
李 鑫,白广忱,王鹞玮
(北京航空航天大学能源与动力工程学院,北京100191)
0 引言
叶盘系统的振动特性对航空发动机整体结构的可靠度有很大影响。实际叶盘系统由于加工、磨损等因素,各扇区之间存在微小差别,称为失谐。失谐会导致系统出现模态局部化和共振区间拓宽等问题,对发动机运行安全造成严重影响。国内外学者对失谐叶盘的振动特性进行了大量研究,取得了很多成果[1-3]。白斌等[4]详细阐述了失谐叶盘结构分析模型、响应局部化、失谐识别与预测等方面的研究现状,并对未来研究方向进行了说明;王建军等[5-7]建立了失谐叶盘系统的集中参数模型,提出3种模态振型局部化的定量描述方法,并对模态局部化现象进行了试验验证;Petrov等[8-9]从优化的角度提出1种判断失谐叶盘系统振动最大响应状态的方法;姚建尧等[10]给出叶盘结构节径谱的数学定义,解释了其物理意义,并利用节径谱的概念对失谐叶盘结构的动态特性进行分析和评价;Ayers等[11]研究了失谐叶盘结构的瞬态强迫响应特性,计算了在加速、减速和通过共振区时的最大应力。以上研究基于确定性分析,对共振状态下失谐造成的模态局部化问题进行了详细说明,但并没有对失谐叶盘系统进行避共振可靠度分析。
在机械结构避共振可靠度分析方面有很多研究成果。王延荣等[12]建立频率干涉模型,并用数值方法就具体问题进行求解;张萌等[13]采用梯型和平顶正态型隶属函数对模态频率的模糊性进行描述,建立避共振模糊可靠度模型;翟红波等[14]基于七点计算法和矩估计法,给出了两端简支输流管道避共振可靠度的计算方法;欧阳德等[15]基于叶片共振转速图,引入概率故障树 PFTA(Probability Fault Tree Analysis)的概念,给出评估叶片避共振可靠度的方法;王鹞玮等[16]建立叶盘结构的有限元模型,得到不同工况下叶盘结构模态频率的概率分布特性和避共振可靠度变化规律。这些研究中提出的避共振可靠度理论对叶盘系统的避共振分析具有重要意义,但并没有根据实际工况,考虑失谐叶盘系统激振频率和模态频率的相关性。
本文考虑失谐叶盘系统激振频率和模态频率的相关性,建立失谐叶盘系统避共振可靠度分析方法,通过对比验证了其准确性,为失谐叶盘系统的避共振设计和研究提供了理论支持。
1 基本理论
1.1 失谐叶盘系统分析方法
忽略阻尼影响的情况下,谐调叶盘结构的运动方程为

式中:M为结构质量矩阵;K为结构刚度矩阵;F为外部激振力向量;x为结构振动的位移向量;x¨为结构振动的加速度。
对叶盘结构中的质量矩阵M和刚度矩阵K进行随机失谐处理[17],分析失谐情况下叶盘系统的振动特性,失谐后的质量矩阵Mλ和刚度矩阵Kλ为
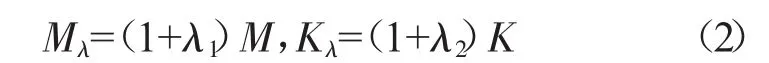
式中:λ1和λ2为表示叶盘结构质量和刚度失谐程度的向量。
由于叶盘结构的模态特性不会受到外部激振力的影响,所以在对失谐叶盘结构进行模态分析时忽略外部激振力的影响,即F=0。则式(1)简化为

本文采用有限元方法对式(3)进行数值求解,得到失谐叶盘结构的各阶模态频率w和对应的模态位移D,对失谐叶盘结构的模态特性进行分析。
1.2 响应面方法
计算结构可靠度的主要模拟统计方法有蒙特卡洛方法、响应面法以及二者结合的混合模拟方法等。虽然蒙特卡洛方法在计算结构可靠度的过程中具有直观、简单的特点,但是对于单次分析需要较长时间的复杂问题,蒙特卡洛方法通常耗时较长,效率极低。响应面法则通过合理的试验设计选取样本点,利用选取的样本点和由样本点计算得到的响应拟合1个响应面来替代未知的真实状态曲面,用得到的响应面进行分析,从而大大提高了计算效率。很多学者针对如何利用响应面法进行可靠性分析做了大量工作[18-21]。
本文采用有限元软件对失谐叶盘系统进行概率分析,计算得到失谐叶盘系统模态频率对随机变量的响应面。采用中心复合设计选取样本点,用不含交叉项的二次响应面对结果进行拟合。不含交叉项的二次响应面为

式中:X=(x1,x2,…,xn),为随机变量。
得到失谐叶盘系统模态频率对随机变量的响应面后,利用考虑激振频率和模态频率相关性的失谐叶盘系统避共振可靠度计算方法进行分析,计算得到避共振可靠度的响应面模型。
1.3 避共振分析理论
1.3.1 激振频率
在避共振分析中,常取叶盘系统的激振力频率f1为发动机工作转速w的整数倍,即

式中:B为结构谐波系数,是1个与叶片所在级的前后级叶片数、级前喷嘴数等因素有关的正整数。合理选取B值也是叶盘避共振的重要措施。根据实际工作过程确定w的均值和标准差ew,则激振频率f1的均值和方差为
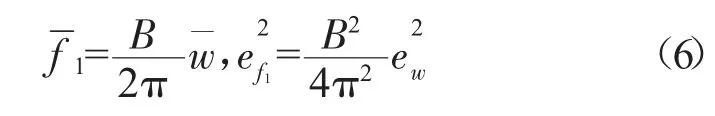
1.3.2 模态频率
本文根据实际工作过程,选定各随机变量的均值和标准差,利用有限元软件计算得到叶盘系统的模态频率f2对各随机变量的响应面为

式中:x1,x2,…,xn分别为材料特性、载荷、工作温度等随机变量。
本文中采用不含交叉项的二次多项式拟和响应面且各随机变量服从高斯分布,根据统计学规律,模态频率f2的均值和方差为

1.3.3 避共振可靠度计算方法
基于文献[22]提出的避共振理论,本文根据叶盘系统实际工作情况,提出考虑激振频率和模态频率相关性的避共振分析方法,对失谐叶盘系统进行避共振可靠度分析。
叶盘系统避共振可靠度Rf是指叶盘系统不发生共振的概率,即叶盘系统模态频率f2避开某转速w引起的激振力频率f1的概率。按照传统的振动设计规范,当f1和f2满足式(10)时,称振动设计是安全的。
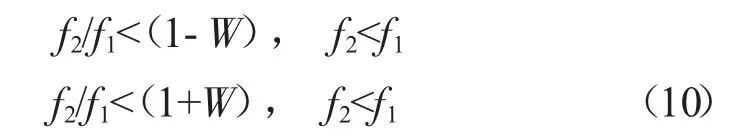
式中:0<W<0.3,为振动设计常数。
给定

用g(f2)表示叶盘系统模态频率分布的概率密度函数,(ff11)和 (ff12)表示激振力频率分布概率密度函数,G(f1,f2)=0 表示叶盘系统的极限状态函数。

根据模态频率分布与激振力频率分布的干涉模型,则系统可靠度为
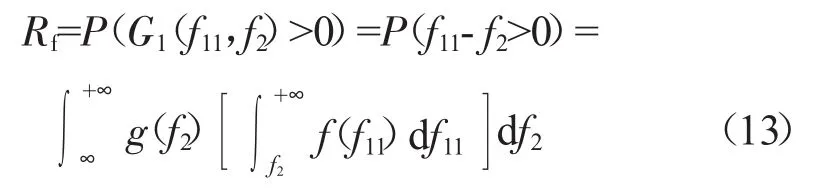
当叶盘系统的模态频率f2和激振频率f11服从正态分布时,极限状态函数G(f11,f2)也服从正态分布,均值EG1和方差DG1为
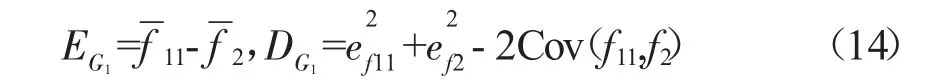
在传统分析中,假设f11和f2是相互独立的,协方差 Cov(f11,f2)=0。但在实际工作过程中,f11和 f2均与随机变量转速相关,有一定相关性,即协方差Cov(f11,f2)≠0。根据 χ2分布的规律,对Cov(f11,f2)进行近似计算
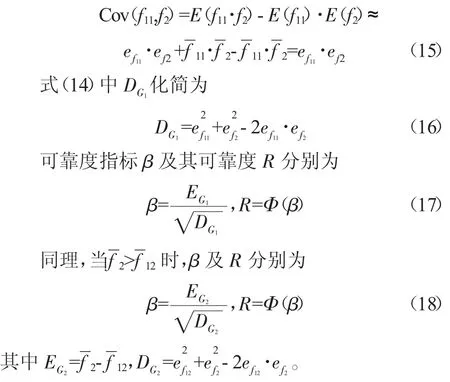
2 失谐叶盘系统避共振可靠度算例
2.1 有限元模型及温度场说明
以某型航空发动机第3级低压涡轮为研究对象,利用UG建立叶盘结构的3维实体模型,导入Hypermesh中划分网格,采用有限元软件进行叶盘结构的振动特性分析。整个叶盘结构共有30个扇区,有限元模型如图1所示,包含296400个单元,342120个节点。单个扇区的有限元模型如图2所示。轮盘半径为160 mm,叶片高度为105 mm,模型选用的材料为镍基变形高温合金GH4133。

图1 叶盘有限元模型
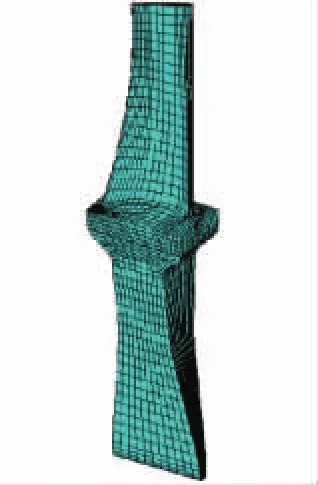
图2 单扇区有限元模型
为使分析过程更加接近叶盘系统的实际工作过程,根据文献[23],对叶片工作温度沿叶高进行线性分布设计,叶片两端温度较低,温度最高值在叶片中部,轮盘部分由于有冷却系统进行冷却,温度梯度较低。采用1维温度场插值方法对叶盘系统沿径向进行分段插值拟合。温度插值方案如图3所示。叶盘系统在有限元软件中按照温度插值方案进行热分析,最终得到的稳态温度场结果如图4所示。
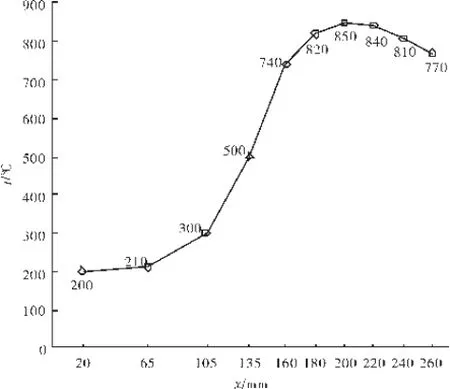
图3 温度插值方案
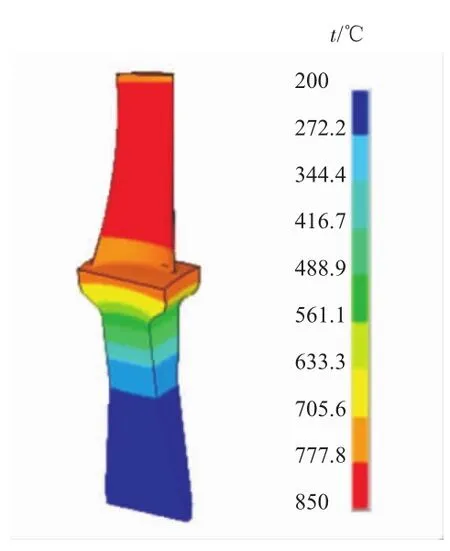
图4 叶盘稳态温度场
为了模拟真实叶盘的失谐状态,本文将叶片和轮盘所包含的单元分开定义属性,将叶片的材料参数和温度场作为分析变量,轮盘的参数是确定的。根据叶盘结构的有限元模型和温度场计算结果,选定叶盘系统的分析变量见表1。

表1 模型参数
表中:E700、E800和 E900分别为 700、800 和 900 ℃下的弹性模量;t160为叶片和轮盘过渡处的温度;t200和t220为叶身中间部分的温度;t260为叶尖处的温度;W920为航空发动机的巡航转速。
2.2 失谐叶盘确定性分析
根据表1数据进行失谐叶盘的确定性分析,得到失谐状态下叶盘系统的模态频率和响应,将结果与谐调状态下的叶盘结构的计算结果进行对比,说明对失谐叶盘进行避共振分析的必要性,为失谐叶盘的概率分析和可靠度计算奠定基础。
随机选定1个叶片,根据表1中的分析参数,将选定叶片上的各参数设置成失谐状态,未选定叶片参数保持不变,以此来模拟真实叶盘系统的失谐状态。利用有限元软件计算失谐叶盘系统的各阶模态频率f2和对应的模态位移D,与谐调叶盘结构进行对比。为了保证分析结果的准确性,选定了a、b、c3种失谐状态,各失谐状态具体参数见表2。
取第2阶模态的计算结果进行分析。第2阶模态在3种失谐状态下的计算结果见表3。谐调叶盘和3种失谐状态下的叶盘对应的第2阶模态振型如图5所示。

表2 谐调和3种失谐状态下的参数
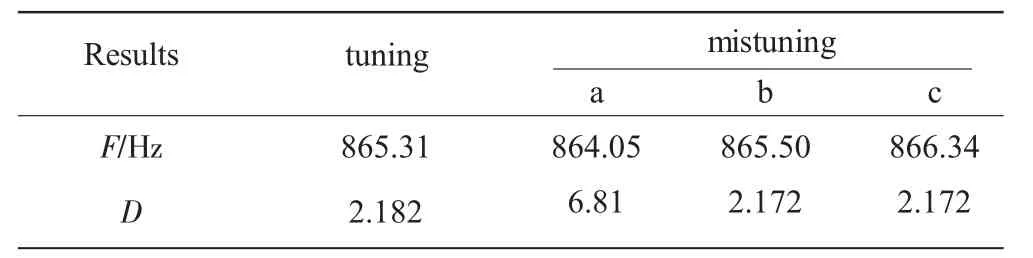
表3 谐调和失谐状态下的第2阶模态频率
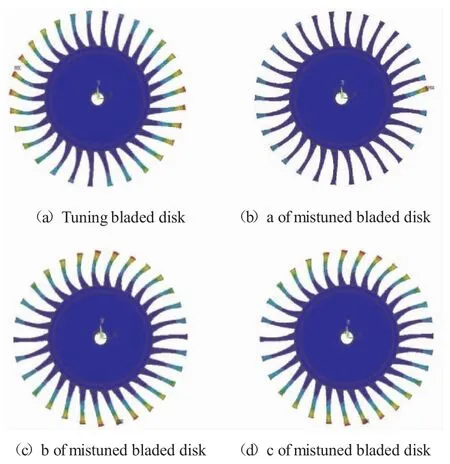
图5 各状态下第2阶模态振型
对表3中的模态频率进行分析,发现失谐导致叶盘模态频率发生分散,降低叶盘系统的避共振裕度,使叶盘结构更容易发生共振,增加叶盘系统避共振难度。对表3中的模态位移和图5中的模态振型进行分析,发现在a失谐状态下,叶盘系统的振型明显不同于谐调状态,并且对应的模态位移也是谐调状态下的3.12倍。说明失谐还会导致叶盘系统出现模态局部化,同时模态位移也会大幅增加。因此,为使叶盘系统避开共振区间,提高叶盘结构的可靠性,进行相应的概率分析和可靠度分析是十分必要的。
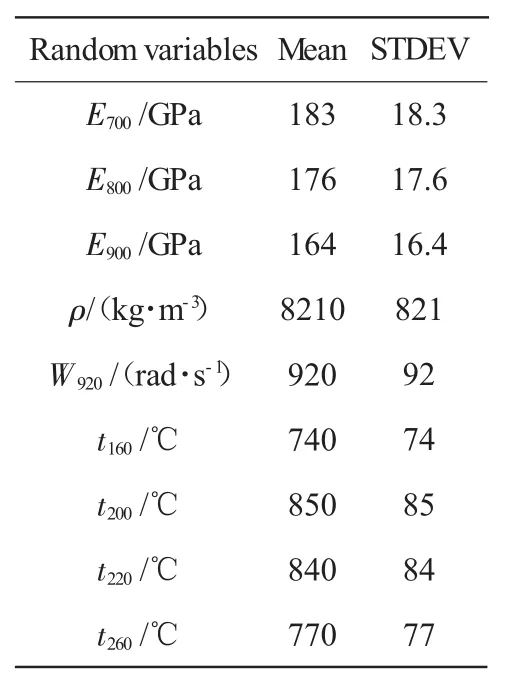
表4 随机变量均值和方差
2.3 失谐叶盘概率分析
失谐叶盘概率分析选择的随机变量和分析方法与确定性分析相同,假定各变量均服从高斯分布且相互独立,均值和标准差见表4。根据确定性分析的结果,选择失谐叶盘系统的第2阶模态频率f2作为输出变量。
利用中心复合设计抽样方法对随机变量进行抽样,抽取149组样本,利用有限元软件计算得到第2阶模态频率,采用不含交叉项的二次多项式进行拟合,最终得到失谐叶盘第2阶模态频率对各随机变量的响应面

为了验证响应面的精确性,利用蒙特卡洛方法,按照随机变量的分布规律抽取10组样本,先采用式(19)中的响应面计算得到对应的第2阶模态频率fs再将各组随机变量分别代入有限元模型计算得到精确的第2阶模态频率fm,计算二者的相对误差,结果见表5。从表中数据可知,由响应面计算得到的第2阶模态频率与真实结果误差很小,说明式(19)中的响应面非常准确。
从式(19)中可见,失谐叶盘系统的第2阶模态频率是转速的函数,在响应面拟合过程中,转速并没有被作为小量被忽略,而从式(5)中可见,激振频率同样是转速的函数,再次证明激振频率与模态频率不可能是2个相互独立的变量。
通过蒙特卡洛方法对响应面进行10000次抽样计算,得到失谐叶盘系统第2阶模态频率f2的概率分布特性,如图6所示。从图中可见,叶盘系统第2阶模态频率大致服从均值为865.66 Hz、标准差为50.49 Hz的正态分布。与谐调叶盘相比,失谐叶盘系统的模态频率拓宽至1个分布区间,增加了叶盘系统发生共振的可能性。
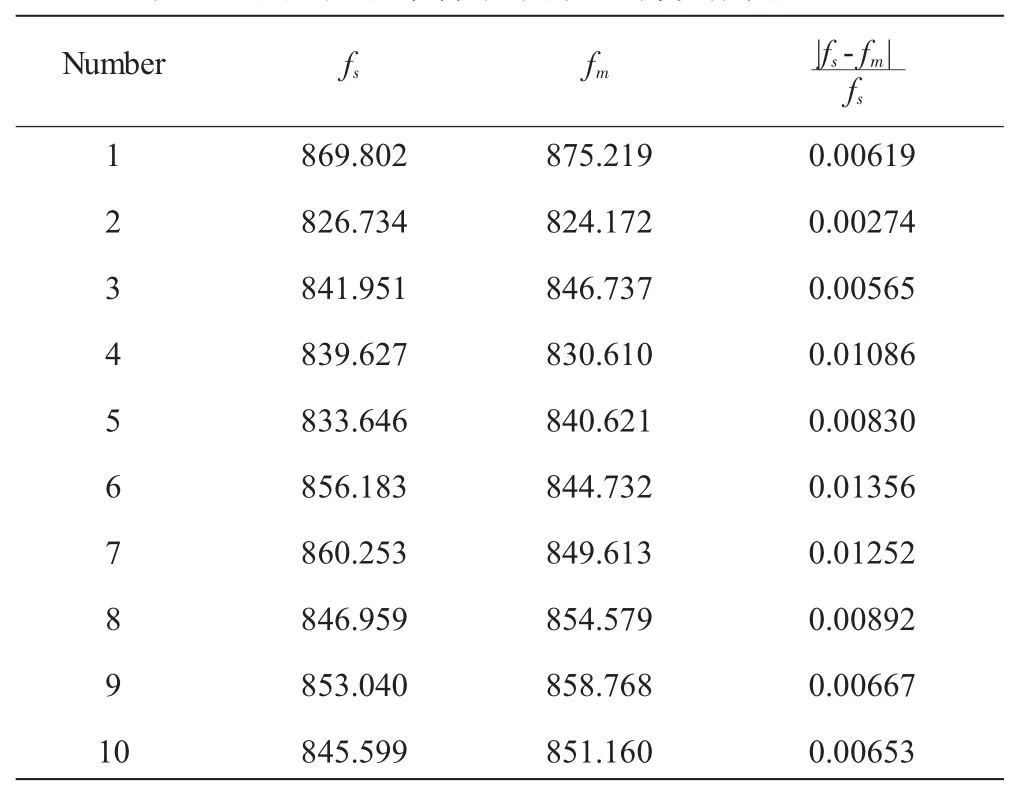
表5 响应面和蒙特卡洛方法计算结果及误差

图6 第2阶模态频率概率分布
2.4 失谐叶盘避共振可靠度分析
根据式(8)、(9),对式(19)进行处理,计算得到失谐叶盘第2阶模态频率的均值和方差

将式(20)~(22)代入式(17)或式(18)中,得到考虑激振频率和模态频率相关性的可靠度模型。
用得到的可靠度模型计算结构谐波系数B取1~8的情况下对应的可靠度Rfc,并与蒙特卡洛法模拟1000次得到的结果Rfm和不考虑激振频率和模态频率相关性的传统方法的结果Rft进行对比,分析本文提出的避共振可靠度计算方法的精确程度,3种方法的计算结果见表6,本文提出方法及传统方法相对于蒙特卡洛方法的相对误差见表7。

表6 不同方法计算下的可靠度

表7 不同方法的相对误差
从表中数据可见,本文提出的考虑激振频率和模态频率相关性的避共振可靠度计算方法相比于传统的可靠度计算方法,计算结果更加接近蒙特卡洛方法的计算结果,说明本文提出的避共振可靠度计算方法能够更加精确地计算真实叶盘系统的避共振可靠度。但是本文提出的方法计算得到的结果一般大于由蒙特卡洛方法计算得到的结果,说明本方法在评估可靠性时会对叶盘系统的避共振可靠度产生过高的估计,需要进一步改进。
比较结构谐波系数B取不同值时对应的的可靠度,可以发现B取值接近6时,叶盘系统的避共振可靠度最低,为0.6239;而B取其他值时,叶盘系统的避共振可靠度均较接近1。说明结构谐波系数B的选取对叶盘系统的避共振设计有重要影响。对于本文中的模型,结构谐波系数B应该尽量选取远离6的值以避免发生共振。在某些情况下,当叶盘系统的结构谐波系数无法更改时,则应将工作转速限制在更合理范围内,并尽量减小转速的随机性。
3 结论
(1)本文参考已有的振动可靠度分析方法,考虑激振频率和模态频率的相关性,建立了失谐叶盘系统的避共振可靠度计算模型。该模型在分析问题时更加接近失谐叶盘系统实际的振动状态,完善了振动可靠度分析方法。
(2)本文对失谐叶盘系统进行确定性分析和概率分析。发现在失谐状态下,叶盘系统的模态频率将会拓展成1个区间,使得叶盘系统更容易发生共振,增加避共振的难度。且在失谐状态下,叶盘系统的模态位移也可能大幅增加,使叶盘系统激振频率经过共振区间时更加危险。所以对失谐叶盘进行避共振可靠度分析具有实际意义。
(3)根据本文提出的考虑激振频率和模态频率相关性的失谐叶盘系统避共振可靠度计算方法得到的计算结果,相比于不考虑激振频率和模态频率相关性的传统方法的结果,与蒙特卡洛方法的计算结果更加接近,说明该方法合理,能够更准确预测叶盘系统避开共振的概率,具有较高的工程应用价值。在分析过程中还发现结构谐波系数同样是影响叶盘系统避共振的重要因素,对叶盘结构的设计具有一定的指导意义。

