基于阵列式工装的薄壁曲面件定位方法研究

张洪双，李向国，何 辉，郑东阳

（河海大学 机电工程学院，常州 213022)

0 引言

工业中一些薄壁曲面类零件如飞机薄壁曲面件等的典型制造工艺是先成型后加工，由于这类零件的刚度小，型面复杂，自身在重力下容易变形，给零件成形后的曲面测量、轮廓划线、裁边、钻孔等加工操作带来了很大的困难。薄壁曲面件的传统加工定位主要依靠具有产品形状特征的模线样板和标准工艺装备，即工装表面需要具有和薄壁曲面件一致的曲面形状。传统的定位方法协调环节多，对零件的准确度影响大，且工装笨重，一套工装只针对一种零件，适应性差，成本高，难以满足各行业日益提高的多品种、小批量的需求。如何实现薄壁曲面件加工定位的柔性化，使同一个工装适用于不同形状和尺寸的薄壁曲面件是国内外研究的热门问题。

国内外对柔性工装技术展开了广泛的研究，文献[1]介绍了可重构工装的重要意义、分类和未来发展；文献[2]介绍了一种手工调节的阵列式柔性工装及零件支撑定位的优化目标函数。文献[3]介绍了一种基于多点的钣金件成型柔性夹具。但以上文献均未涉及到曲面零件的定位问题。文献[4]通过特征曲面、曲率匹配来实现曲面匹配的初定位及精调整，计算过程较复杂，需要较多次的迭代计算，这类方法主要用于曲面测量、非定位/欠定位加工等方面。文献[5]提出了用OBB方法对曲面零件定位，但定位精度较低。

目前国外对于薄壁曲面件的加工装配主要通过阵列式柔性工装来实现零件的定位和支撑，阵列式柔性工装的工作区域通常可用一个正六面体来表述，薄壁曲面件的定位问题可通过求取包络薄壁曲面件的正六面体包围盒，根据包围盒和工装工作区域的相似性来确定坐标变换矩阵中的6个参数值，即求取薄壁曲面件的包围盒。为了提高支撑定位的稳定性，应使曲面零件与工装中柔性单元尽可能多的接触，即曲面在工装平面内的投影面积最大。

本文根据工业实际需求和薄壁曲面件的加工特点，根据碰撞检测中常用的包围盒方法计算出薄壁曲面件的包围盒，根据包围盒与柔性工装工作区域的相似性对薄壁曲面件进行预定位；然后对包围盒进行旋转迭代求出包围盒在工装平面内的最大投影面积，实现薄壁曲面件的精定位，并根据两次定位过程确定坐标变换矩阵中的参数值，为曲面方程求解提供了条件。

1 N-2-1 定位原理和柔性工装结构

传统的针对刚体的3-2-1定位方法和工装设备难以满足薄壁曲面件的加工要求。从柔性的角度考虑，工装除了实现零件定位还要实现零件的保形，阵列式柔性工装要可调整，使其具有薄壁曲面件的曲面形状。这类零件可以采用 N-2-1定位方法（N≥3）[6]，如图1所示。

图1 柔性工装示意图[7]

柔性单元在工装底座上以阵列形式分布，对应着主基准面的N个定位点，用于实现薄壁曲面件的定位和保形。柔性单元采用模块化方法设计，其数量可根据工件的尺寸进行调整，使柔性工装能够满足不同薄壁曲面件零件的加工需求。

2 薄壁曲面件的包围盒

考虑到包围盒的紧密性，采用方向包围盒（Oriented Bounding Box，OBB）。一个给定对象的OBB定义为包含该对象且相对于坐标方向任意的最小正六面体，OBB的最大特点是方向的任意性，可根据对象的形状特点尽可能紧密的包围对象。在其包裹状态下，可以较好的实现薄壁曲面件的初定位。

2.1 协方差方法求解OBB包围盒

OBB计算的关键是寻找到最佳方向并确定在该方向上的包围盒的最小尺寸。文献[8]提出了对曲面控制顶点求解包围盒的方法，但包围盒的尺寸较大，包裹性较差。这里直接求解薄壁曲面件的曲面上的数据点的包围盒，根据曲面的参数化方程式，对参数u，v进行取值，设Pi,j为曲面上对应参数ui，vj的一个点，则曲面上点集的协方差矩阵为：

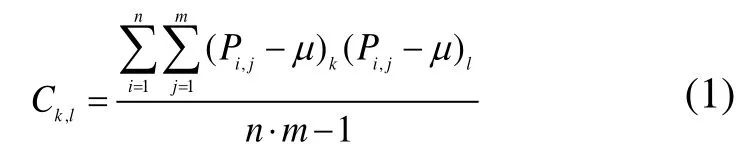
式中，k,l=1,2,3，μ为曲面的重心点。协方差矩阵C的3个特征向量是正交的，归一化可作为一个基底R用于确定OBB的方向。R的表示形式为：

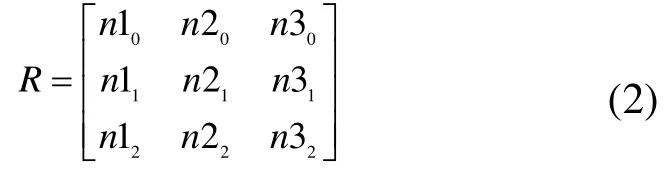
式中n1，n2，n3为协方差矩阵的归一化特征向量，表示OBB的三个方向。如图2所示为某曲面的OBB包围盒，n1、n2、n3分别为包围盒的3个方向，P点为包围盒的一个顶点。

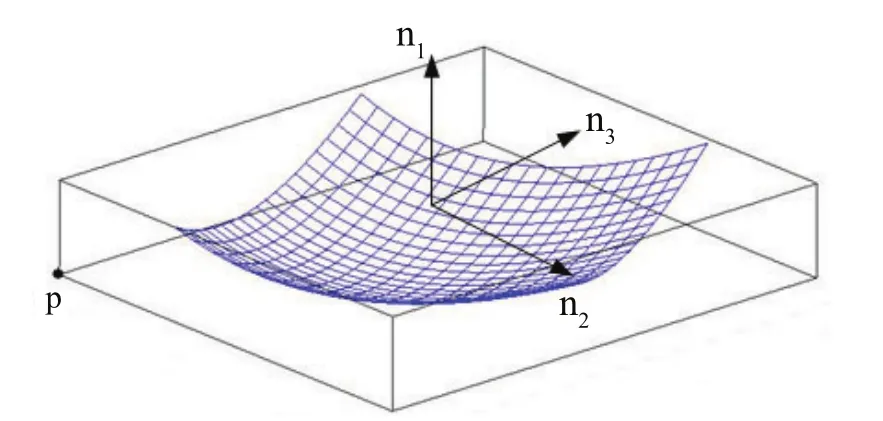
图2 曲面的包围盒

2.2 基于包围盒的预定位

对包围盒进行旋转，使其n1、n2、n3的三个方向分别和图2所示的工装中Z、X、Y轴相对应，求取变换矩阵中的3个角度参数α1、β1、γ1。其表达式分别为：

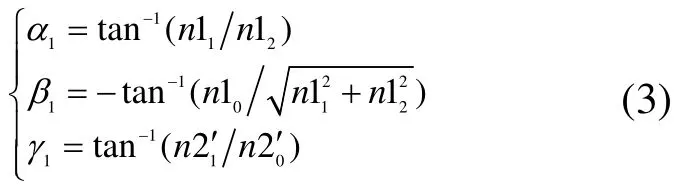
其中，n2’为矢量n2经过α1、β1旋转变换后的矢量。找出各方向的极值点（xmin，ymin，zmin）（xmax，ymax，zmax），得到其包围盒OBB。各角度值1α、1β、1γ，为初定位的旋转坐标变换矩阵T1中的角度值。

2.3 基于包围盒迭代法的精定位

上述过程求取的OBB可以满足曲面的预定位要求，但不是最优的结果。可通过迭代算法进行精定位，迭代过程的实质是在工装平面内最大投影面的面积最小化问题，具体步骤为：

1）将方向包围盒绕Y轴旋转变换，使变换后的薄壁曲面件的方向包围盒在XY平面内的投影面积最大。在投影面积最大时，其旋转角度定义为

2β；

2）将方向包围盒绕X轴旋转变换，使变换后的薄壁曲面件的方向包围盒在XY平面内的投影面积最大。在投影面积最大时，其旋转角度定义为

2α；

3）将方向包围盒绕Z轴旋转变换，使变换后的薄壁曲面件的方向包围盒在XY平面内的投影面积最小。在投影面积最小时，其旋转角度定义为γ2。

经过步骤1）和2）后包围盒在XY平面内的投影面积最大，此时曲面类零件与柔性单元相接触的数量最多。但对于阵列式的柔性工装而言，此时参与工作的柔性单元的行列数量较多，不是一个最优结果，经过步骤3）处理后可以有效减少参与工作的柔性单元行列数量，在柔性单元行列数量相同的情况下，能够满足更大尺寸的曲面类零件的需求。

在上述步骤中包围盒绕各轴旋转获得投影面积最小值时的角度值α2、β2、γ2，为精定位旋转坐标变换矩阵T2中的角度值。

3 工装坐标系下的曲面方程

薄壁曲面件经过两次旋转变换后包围盒顶点P的坐标值为（xP、yP、zP），使点P和工装上的参考点D（xD、yD、zD）（工装上的某个指定点）重合，可求变换矩阵中的3个平移参数l、mn，其表达式为：

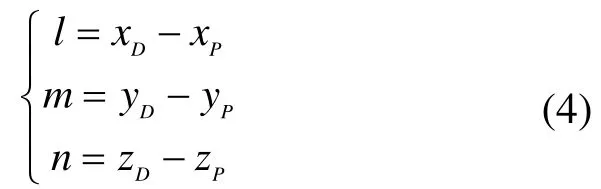
柔性工装坐标系为ΣM，薄壁曲面件的坐标系为ΣS，则薄壁曲面件在柔性工装坐标系中定位过程可由转换矩阵T来描述，具体可写成为：

式中，Ti（i=1,2）和T3分别表示为：

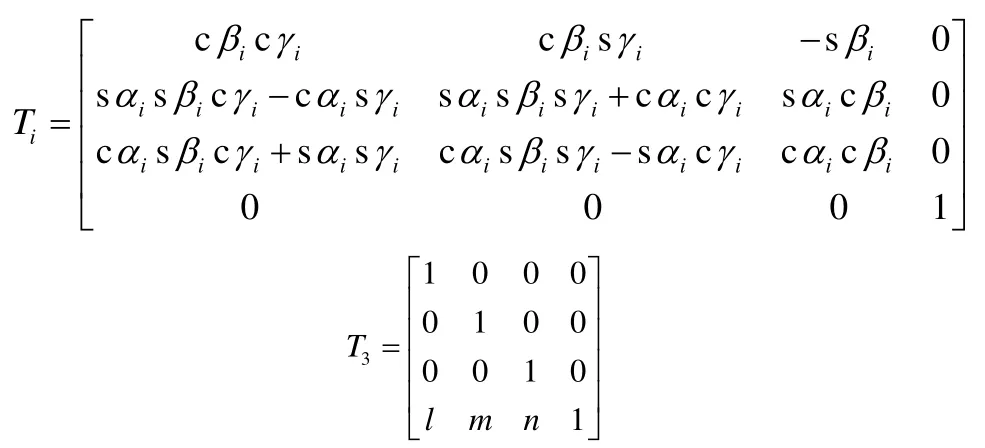
式中，字母c表示cos函数，字母s表示sin函数。

薄壁曲面件的外形常采用B样条曲面进行描述，其表达式为：

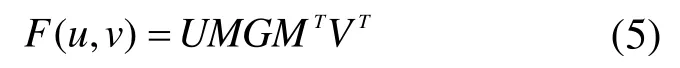
式中：u，v 为参变量， U = [ 1 u u2u3]，V =[1 v v2v3]，M为常数矩阵，G为控制顶点矩阵。B样条曲面的几何信息完全包含在控制顶点矩阵G中，所以薄壁曲面件在工装坐标系中的方程可通过零件数模的控制顶点来实现，即工装内的薄壁曲面件曲面方程可表示为：

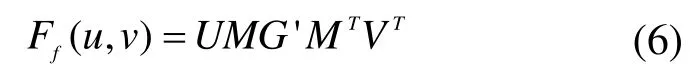
式中， 'G GT= 。

4 算法验证

根据前面所述，利用MATLAB对计算过程进行验证。已知某薄壁曲面件的拟合等距曲面控制顶点G为：

取工装上参考点D的位置坐标为（0,0,0），根据柔性工装和柔性单元的结构尺寸，取柔性单元的初始位置坐标为（100mm,100mm），X向间距为200mm，Y向间距为200mm。分别采用OBB方法和OBB迭代方法对该曲面进行分析，两种不同方法的结果如表1所示。

由分析结果可见，在采用OBB迭代方法后，曲面零件的包围盒在XY平面投影减小的比例较大，但柔性单元在Z向的高度总和变化不大。经过OBB迭代后，支撑薄壁曲面件的柔性单元的行列数量均有减少，使同一个薄壁曲面件在工装内的覆盖面积更小，同一个柔性工装能最大限度的满足大尺寸零件的需求。

5 结论

基于阵列式的柔性工装可有效解决传统的薄壁曲面件加工工装的不足之处，满足薄壁曲面件加工过程中对工装柔性化的需求。本文对阵列式柔性工装的薄壁曲面件定位算法进行了分析和研究，结论如下：

1）薄壁曲面件的准确定位和保形问题可以通过阵列式柔性工装来解决；

2）基于N-2-1的定位方法可以有效解决薄壁曲面件的定位并实现零件外形的保持；

3）通过包围盒及其迭代法实现坐标变换矩阵的求解，迭代次数少，方法直观，易于实现。

在薄壁曲面件准确定位和保形的基础上，进一步的工作主要在拟合曲面的误差分析以及柔性单元的布局优化等。

[1] Bi Z, Lang S, Verner M,Orban P. Development of

reconfigurable machines[J].The International Journal of

Advanced Manufacturing Technology 2008;39:1227-1251.

[2] Sela MN,Gaudry O,Dombre E,Benhabib B.A reconfigurable modular fixturing system for thin-walled flexible objects[J].The International Journal of Advanced Manufacturing Technology.

[3] Munro C,Walczyk D. Reconfigurable pin-type tooling:a

survey of prior art and reduction to practice[J].Journal of manufacturing science and engineering 2007;129:551.

[4] 徐金亭,孙玉文,刘伟军.复杂曲面加工检测中的精确定位方法[J]. 机械工程学报.2007.43:175-179.

[5] Zhang Hong-shuang, JI Ai-min . Algorithm research based on multi-point locating for compliant part. Conference on Modelling and Simulation (ICMS2010).Volume 2:80-83.

[6] W.Cai,S.J.Hu,J.X.Yuan.Deformable Sheet Metal Fixturing: Principles,Algorithms,and Simulations[J].Journal of Manufacturing Science and Engineering.1996(118):318-324.

[7] CAN fixture flexible tooling system[EB/OL].http://www.cnaflex-tool.com/cnaflxtool.

[8] Francis Page,Francois Guibault.Collision Detection Algorithm for NURBS Surface in Interactive Application[J].CCECE 2003-CCGEI 2003,Montreal,May 2003:1417-1420.