基于LCL滤波的三电平APF研究
刘晓雷,李静
(中国矿业大学 信息与电气工程学院,江苏 徐州221008)
1 引言
目前,电网中的无功和谐波污染日益严重,不仅降低了电能的生产、 传输和利用效率,同时也降低了电气设备运行的可靠性,甚至损坏设备、 危及电网的安全。 并联型有源电力滤波器(active power filter,APF)在实际使用中相当于电流源,可以用于补偿上述电流型谐波。 同时,为满足电力电子设备向高压大功率方向发展的要求,选用基于二极管钳位型三电平变流器作为APF 的主电路拓扑,可以有效地提高APF 补偿容量,降低功率管开关损耗以及减少变流器输出谐波含量。
在APF 工作过程中,会产生大量开关频率附近的谐波,因此需外加滤波装置,传统的L型滤波器结构简单,成本低,但其衰减率较低,为达到滤波效果,必须使滤波电感足够大,而这又将导致补偿电流跟踪困难。 文献[1-2]采用3 阶LCL 滤波器代替传统的L 型滤波器,可以兼顾低频段增益和高频段的衰减,达到良好的效果,但其参数选择方法只适用于两电平拓扑结构。 本文在前人的基础上,以三电平APF为研究对象,通过理论分析推导了适用于三电平变流器的LCL 滤波器参数选择依据。
补偿电流的跟踪对APF 的性能有着较大的影响,由于APF 的指令电流为变化率较大的交流量,传统的PI 控制很难做到无静差,新型的自适应控制、 模糊控制等设计复杂,不利于工程实现。 广义积分器可以对正弦周期量实现无差调节,文献[3-4]将其用于APF 电流跟踪控制,但只适用于平衡系统。 文章采用改进型二阶广义积分器,不仅能够实现对各次谐波的无差调节,而且克服了电网电压正、负、零序问题对积分器的影响,取得了良好的效果。
2 三电平APF 数学模型及LCL 滤波器参数设计
2.1 三电平APF 数学模型
基于LCL 滤波的三电平APF 拓扑结构如图1所示。

图1 三电平APF 主电路Fig.1 Three-level APF main circuit
图1中,ea,eb,ec分别为三相电网电压,L1为变流器侧滤波电感,L2为电网侧滤波电感,Cd为滤波电容,Rd为阻尼电阻。
根据基尔霍夫电压定律和基尔霍夫电流定律,得到三电平APF 在abc 坐标系下的数学模型为
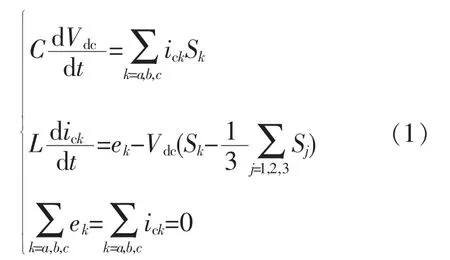
式中:C 为直流侧母线电容值;Vdc为直流侧电容电压;L 为等效纹波电感;ick为补偿电流;ek为电网电压;Sj(j=1,2,3) 分别对应各桥臂输出-1,0,1 状态。
2.2 LCL 滤波器参数设计[5-7]
为了便于对LCL 滤波器原理进行分析,将L1,L2和Cd作为研究对象,建立基于LCL 滤波器的单相等效电路如图2所示。 从图2中可以看出,L2支路和电容支路并联,然后再与L1串联,电流i2为L2支路和电容支路对电流i1的分流。
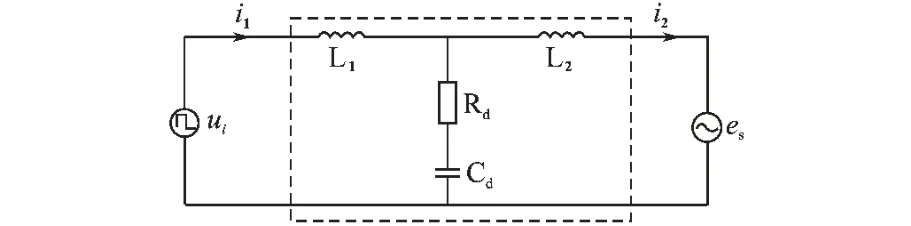
图2 LCL 滤波器等效电路Fig.2 Equivalent circuit of LCL Filter
省略推导过程,得到LCL 滤波器的频域特性方程为

由式(2)可以看出,LCL 滤波器是一个3 阶系统,各参数相互耦合作用,给参数设计带来了一定难度,且参数选择不当,容易引起电网谐振。
2.2.1 L1的设计
从电路的角度分析,电容支路对高频分量相当于短路,电容支路和L2支路的并联阻抗近似为零,因此,电流i1是由L2自身的感抗决定的,所以,L1的取值主要考虑对i1纹波电流的抑制。
对于三电平变流器,由磁性元件伏秒平衡原理可以得到变流器侧纹波电流峰峰值为

式中:Vdc为直流侧电容总电压;Vph为电网相电压有效值;L1为变流器侧滤波电感;D 为变流器每一相对直流侧电容中点的占空比;fsw为开关频率。
由极大值原理,假设|D|=0.5,选择Vdc=1 000 V,Vph=220 V,fsw=10 kHz,并根据实际变流器输出电流,取△ILMAX=3.5 A,得到L1的取值约为2 mH。
2.2.2 L2的设计
假设总电感L=L1+L2,在L 一定的情况下,L1和L2的比例关系对滤波效果也有影响,令L=aL1,代入式(2)得到:

经过分析与仿真验证,当a=0.5 时滤波效果最好,但L1过小会增大电容支路的损耗,因此在实际使用时一般选择a>2。
2.2.3 Cd的设计
引入电容支路主要是给电流高频分量提供一个低阻通路,实现对纹波分量的分流,电容越大,谐振尖峰越小,但同时也会导致系统高频部分衰减减慢,因此应保证电容的容抗小于L2阻抗的20%。
2.2.4 谐振频率ωn的选择
电容Cd与L1,L2构成了振荡电路,其谐振频率点为

LCL 滤波器的设计要避免谐振频率与电路谐波源重合,并远离开关频率。 实际使用中常选择10 倍基波频率与0.5 倍开关频率之间。
通过上述分析,综合考虑各参数的相互作用,选择L1=1.6 mH,L2=0.6 mH,Cd=10 μF,Rd=1 Ω,则此时谐振频率为2.41 kHz,符合设计要求。该LCL 滤波器的频率特性波德图如图3所示,图中同时给出单电感型滤波器波德图以作对比。
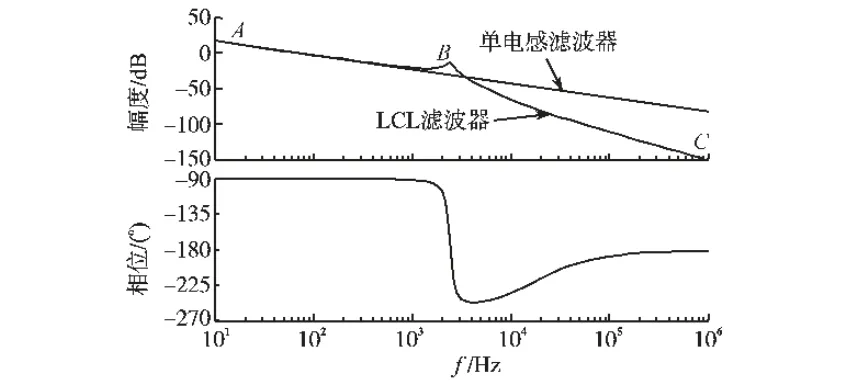
图3 LCL 滤波器频率特性Fig.3 Frequency characteristics of LCL filter
从图3中可以看出,LCL 滤波器在AB 段衰减斜率为-20 dB/10 倍频程,BC 段衰减斜率为-60 dB/10 倍频程,满足系统低频段增益和高频段衰减的设计要求,而单电感滤波器在整个频段内都以-20 dB/10 倍频程衰减,因而对高频段的衰减较弱。
3 基于广义积分器的电流跟踪算法
广义积分器可以实现对正弦量的积分,它在设定的频率处增益无穷大,而对其他频率幅值衰减非常大。 三相电网中的谐波电流主要有5 次、7 次、11 次和13 次等,因此可以采用广义积分器 对主要谐波进行单独控制[3-4]。
传统的广义积分器传递函数为

将其与比例调节器结合,即PR 控制器,可以实现针对特定频率谐波信号的无差跟踪,其传递函数为

在实际电网中,允许频率有小范围的波动,或当电网电压不平衡时,存在着正序、 负序和零序3 个电压分量,这将对控制器的设计带来一定的影响。 文章采用改进的PR 控制器克服上述问题的影响。
改进的PR 控制器传递函数如下:

式中:ωc为截止频率。 ωc越大,带宽越大,而带宽增大,也增加了控制器对电网畸变的适用程度。在特定频率处,R 控制器的幅值增益不再是无穷大,而为KI,此时,可以通过调节KI使其获得足够大的增益,从而保证稳态误差为零。
4 仿真与实验验证
4.1 仿真验证
为了验证基于LCL 滤波的APF 系统的正确性,首先搭建Matlab/Simulink 仿真模型进行仿真验证,控制器主要针对含量较高的5 次、7次、11 次和13 次谐波。 仿真参数如下:电网线电压380 V/50 Hz; 非线性负载为二极管不控整流桥带8 Ω 负载电阻; 直流侧母线电压为1 000 V;变流器侧滤波电感L1=1.6 mH;电网侧滤波电感L2=0.6 mH;滤波电容Cd=10 μF;阻尼电阻Rd=1 Ω。

图4 补偿前三相电流波形Fig.4 Three-phase current before compensation

图5 补偿后三相电流波形Fig.5 Three-phase current after compensation

图6 补偿后a 相电流频谱分析图Fig.6 Spectrum analysis diagram of phasc-a after compensation
图4和图5分别为补偿前、 后三相电流波形,图6为补偿后a 相电流频谱分析图。 从图6中可以看出,补偿后三相电流基波正弦,畸变率只有1.91%,各主要次谐波都得到了很好的抑制。
4.2 实验验证
采用DSP+FPGA 控制系统,其中选择TI 公司TMS320FM28335 作为主控芯片,与FPGA 配合使用。 实验装置原理图如图7所示,采样电路将采样信号传输给DSP,DSP 通过一系列运算得到ePWM 寄存器比较值并将其传输给FPGA,FPGA 取反加死区后经驱动电路控制IGBT 的通断,达到控制变流器的目的。 实验参数与仿真参数一致,IGBT 开关频率为10 kHz。

图7 实验装置原理图Fig.7 Experimental principle diagram
图8为补偿前a 相电流波形,图9为补偿后a 相电流波形。可以看出,补偿后电流基本正弦,基于LCL 滤波的APF 系统有着良好的谐波补偿功能。

图8 补偿前a 相电流波形Fig.8 Phase a current before compensation
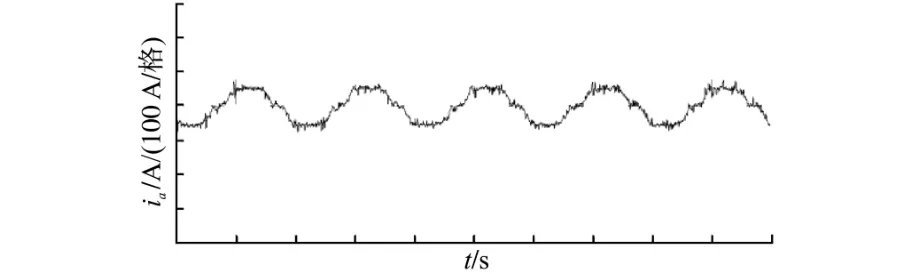
图9 补偿后a 相电流波形Fig.9 Phase a current after compensation
5 结论
针对并联APF 纹波电感的设计,文章采用3 阶LCL 滤波器代替传统的L 型滤波器,在数学模型的基础上,论述了适用于三电平变流器的参数选型方案。 电流跟踪控制采用改进型二阶广义积分器算法,消除了稳态误差,能够克服电网频率小范围波动对积分器的影响。 仿真与实验均表明该APF 系统正确有效。
[1] 张东江,仇志凌,李玉玲,等.基于LCL 滤波器的高稳态性能并联有源电力滤波器[J].电工技术学报,2011,26(6):137-143.
[2] MAGUEED F A,SVENSSON J.Control of VSC Connected to the Grid Through LCL-filter to Achieve Balanced Currents[C]∥Fourtieth IAS Annual Meeting Conference Record.[S.I.]:IEEE,2005: 572-578.
[3] 杨秋霞,梁雄国,郭小强,等.准谐振控制器在有源电力滤波器中的应用[J].电工技术学报,2009,24(7):171-176.
[4] 盘宏斌,罗安,彭可,等.混合型有源滤波器与静止无功补偿器组成综合补偿系统的电流控制[J].中国电机工程学报,2009,29(31):73-79.
[5] 王晓刚,王佳庆,张杰.基于LCL 滤波的有源电力滤波器预测电流控制[J].电气传动,2011,41(9):30-33.
[6] 李泉峰,杨淘,吕征宇.基于PQR 理论的三电平LCL 滤波器优化设计[J].电力电子技术,2011,45(5):27-28.
[7] 张国荣,李宗钧,陈鹏.并联有源电力滤波器中LCL 滤波器的分析与设计[J].高压电器,2011,47(6):19-22.