双旋轮数控旋压机床同步控制技术

王启行，龚时华

（华中科技大学 制造装备数字化国家工程研究中心，湖北 武汉430074）

1 引言

随着制造业发展的需要，旋压机床越来越广泛地运用于机械、汽车、航空、航天等行业零部件的生产。 为了提高生产效率，双旋轮很快被引入到旋压机床。 因此对双旋轮旋压机床的运动控制提出了更高的要求：1）要求2 个旋轮在运动过程中能够保证位置和速度的同步；2）要求系统具有很快的响应速度。

而双旋轮旋压机床的机电液的控制中却存在着诸多影响旋压机床精度因素：1）由于每一个液压系统的泄漏、控制元件间的性能差异、各执行元件间负载的差异、系统各组成部分的制造等误差因素的影响[1]，2 个旋轮在加工过程中会存在同步误差；2）对电液伺服系统而言，由于伺服阀的磁滞，油液的可压缩性等因素的影响[2]，控制系统的响应特性存在着一定的滞后。

双旋轮旋压机床加工过程中的这些误差因素将对系统的静态特性和动态特性产生很大影响，如果不有效地加以控制并克服，加工出来的零件精度将不符合要求。 因此，必须采取措施减小加工过程中的误差，实现双旋轮旋压机床的同步控制。

2 同步控制系统描述

双旋轮数控旋压机坐标系示意图如图1所示，2 个旋轮分别位于2 个坐标系X1O1Z1和X2O2Z2中，Z1和Z2都平行于主轴（或者和主轴成相同的角度），X1和X2分别垂直于Z1和Z2，原点O1和O2由硬件确定其位置。

旋轮的横向运动由位于主轴两侧的液压伺服轴X1和X2驱动，纵向运动由位于主轴两侧的液压伺服轴Z1和Z2驱动。 X1和Z12 个轴构成一个坐标系，合成旋轮1 的运动；X2和Z22 个轴构成一个坐标系，合成旋轮2 的运动。 在加工过程中，通常情况下要求2 个旋轮同时工作，所以要求X1轴和X2轴，Z1轴和Z2轴之间达到位置同步和速度同步。

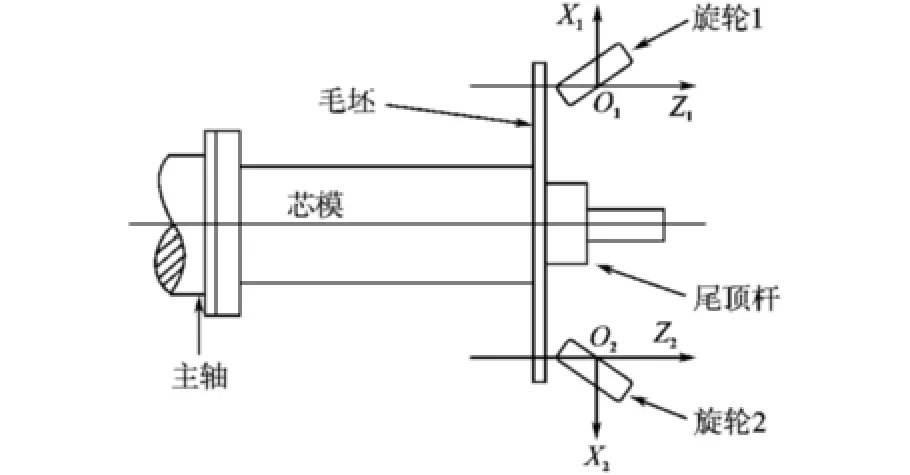
图1 双旋轮旋压机坐标系示意图Fig.1 Coordinate system of double-roller spinning machine

由于两组同步运动规律相同，下文仅对X1轴和X2轴的同步运动进行分析。 为了达到两轴之间同步，设计了两种同步控制方式，分别为并行控制方式和主从控制方式。

并行控制方式的原理图[3]如图2a 所示，X1轴和X2轴的输入完全相同，并且要求各个环节的元器件完全相同，负载也要完全相同。

主从控制方式的原理方框图如图2b 所示，X1轴作为主动轴，X2轴作为从动轴，X1轴的反馈作为X2轴的理想输入。

图2 同步控制原理图Fig.2 The principle diagram of synchronous control

3 同步控制系统的数学建模

由图2可以看出，同步控制系统包含的元件主要有伺服功率放大器、伺服阀、液压缸、光栅尺等。 为了对两种同步控制方式进行分析，必须对各元件建立数学模型。

伺服功率放大器的作用是将偏差电压信号成比例地转化为相应的电流信号，此电流信号输入到伺服阀力矩电机控制线圈，控制伺服阀阀芯开度大小。 将各个参数都换算为国际单位制，得到其开环传递函数为

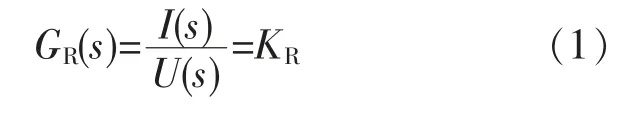
式中：KR为回路增益。

伺服阀是实现电信号向液压信号转化的关键元件，可以运用小功率的电信号来控制大功率的液压动力，很好地将机电液技术结合在一起。伺服阀的开环传递函数为[2]

式中：Kv为伺服阀流量增益；ωv为伺服阀固有频率；ζv为伺服阀阻尼系数。

液压缸是执行元件，它驱动各轴向相应的方向运动，其开环传递函数为

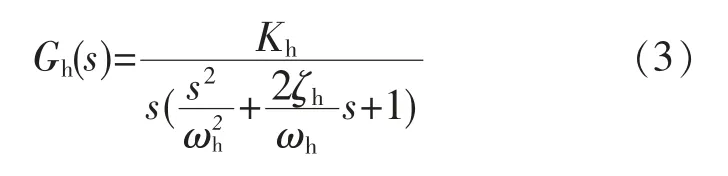
式中：Kh为液压油缸增益；ωh为油缸固有频率；ζh为液压阻尼系数。

由式（1）～式（3）可以得出单回路的开环传递函数G（s）为

4 同步控制系统的仿真

为了比较图2所示的两种同步控制方式，下面运用Simulink 仿真软件对同步控制系统进行仿真。

根据同步控制系统各环节的开环传递函数，建立控制系统模型。 由图2a 所示的原理图，结合式（1）～式（3）建立图3所示的仿真模型。 由图2b所示的原理图，结合式（1）～式（3）建立图4所示的仿真模型。

运用图3和图4所示的仿真模型进行仿真实验，对PID 参数进行整定以后[4]，在没有干扰的情况下，输入信号为4sin（4t）的正弦信号，X1轴和X2轴的响应曲线如图5所示。 在2.3 s 时，给系统一侧加入一个扰动阶跃信号，X1轴和X2轴的响应曲线如图6所示。

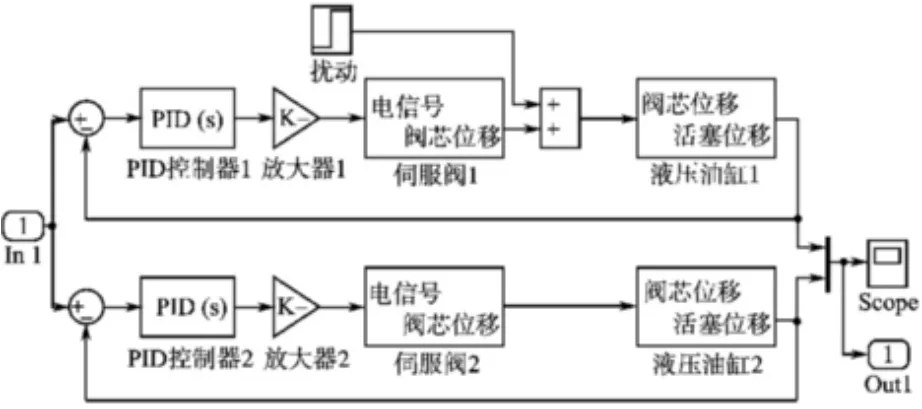
图3 并行控制方式模型Fig.3 Parallel control model

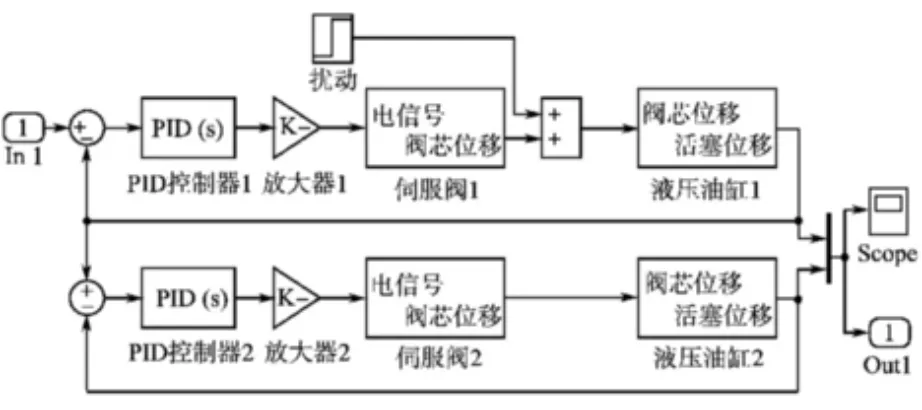
图4 主从控制方式模型Fig.4 Host/Slave control model

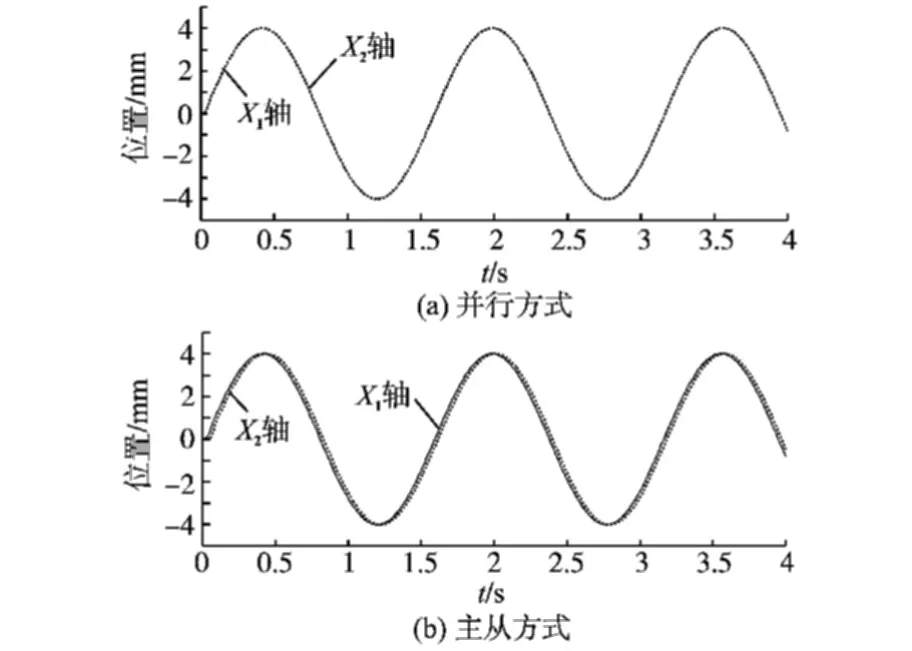
图5 输入4sin（4t）的正弦响应曲线（无干扰）Fig.5 Sine response curves when inputis 4sin(4t) without disturbance

由图5所示的正弦响应曲线可以看出，在没有干扰的情况下，并行系统可以保证X1轴和X2轴的运动完全一致，主从系统却一直存在着一定的滞后，但是两者的位置误差保持在0.018 mm 左右。

由图6所示的正弦响应曲线可以看出，在有干扰的情况下，并行系统相对误差明显增大为0.02 mm，并且在后面一直存在，这个相对误差会一直积累，值会越来越大，这个对于双旋轮旋压机是不允许的，明显影响其产品的精度。 而对于主从系统，扰动对系统的同步性影响很小，两个轴在短时间内的相对误差稍微变大，但是相对误差很快就重新恢复到原来的0.018 mm 以内。 对于双旋轮旋压机来说，只要相对误差保持稳定，对产品的精度影响很小。

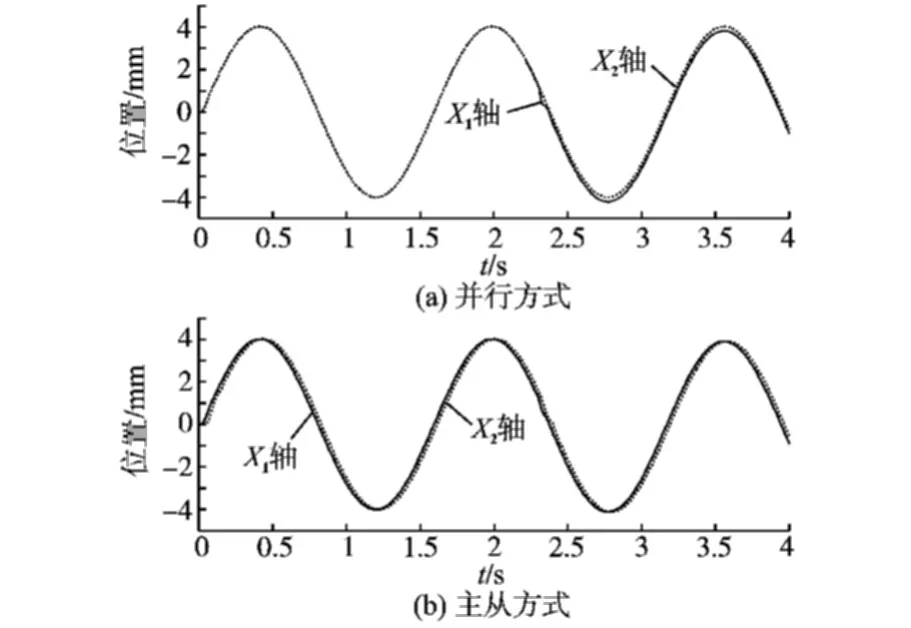
图6 输入4sin（4t）的正弦响应曲线（有干扰）Fig.6 Sine response curves when inputis 4sin(4t) with disturbance

在旋压加工的过程中，由于坯料变形的不均匀性，两个旋轮的负载很可能存在不一致性，所以并行系统在旋压机上面很难得到应用。 因此，可以选择主从同步控制方式作为双旋轮旋压机的控制方式。

5 主从同步控制滞后补偿方法

由图5b 和图6b 所示的正弦响应曲线可以看出，对于主从同步控制方式，从动轴一直存在着一定的响应滞后，原因是：1）液压系统存在着一定的滞后；2）在加工过程中存在电气延迟和机械传动的延迟；3）负载的变化对速度产生影响；4）由式（4）可以看出，传递函数G（s）的分母是5阶，由于分母阶数越大，G（s）的相位滞后越大，所以该系统存在着一定的滞后。

因此，在从动系统中，除了普通的PID 控制外，还需要加入一个前馈控制器对这个滞后进行补偿，因为加入速度和加速度前馈以后，跟随误差能够减小80%。 前馈控制器的结构如图7所示，前馈控制器的表达式为

式中：Kp，Ki，Kd分别为比例、积分、微分增益；Kvff为速度前馈；Kaff为加速度前馈；k 为采样信号，k=0，1…；uk为第k 次采样时刻的输出值；ek为第k次采样时刻输入的偏差值；ek-1为第k-1 次采样时刻输入的偏差值，rk+1为第k 次采样时给定的k+1 时刻指令位置值；rk为第k-1 次采样时所给定的k 时刻指令位置值；vk+1为第k 次采样时给定的k+1 时刻指令速度值；vk为第k-1 次采样时所给定的k 时刻指令速度值。

速度前馈用于减小系统阻尼带来的跟随误差（跟随误差与系统的运动速度成正比），它将速度要求成比例地增加到控制输出上，提高响应的灵敏度； 加速度前馈用于减小由于系统惯性引起的跟随误差 （跟随误差与系统的加速度成正比），它将一个期望的加速度成比例增加到控制输出上。 前馈控制器的引入，能克服同步控制系统的机械惰性，使速度和加速度达到同步跟随的要求。

前馈控制器结构图如图7所示。

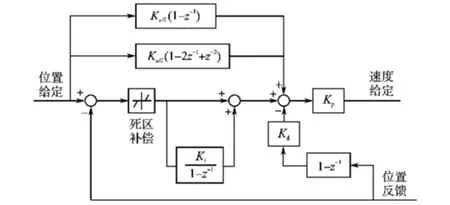
图7 前馈控制器结构图Fig.7 Feedforward controller structure

将图7所示的前馈控制器加入到从动轴的一侧，整定好参数[5]以后，再次输入4sin（4t）的正弦信号，得到的响应曲线如图8所示。

将图8和图5b、 图6b 进行比较可以看出，加入前馈控制器后，从动轴的滞后得到明显改善，误差减小，曲线跟踪更加准确。 除了启动时很短时间内的调整外，其他时间位置误差保持在0.001 mm 以内，同步性很高。

图8 加入前馈控制器后同步控制系统响应曲线Fig.8 Synchronous control system response curve after adding feedforward controller

6 结论

本文研究的双旋轮数控旋压机的同步控制方式，能够有效地实现2 个旋轮的速度同步和位置同步，克服液压系统的滞后性，达到了数控旋压机快速响应的要求，实现了双旋轮数控旋压机的高精度控制。其研究成果已成功运用于某航天系统双旋轮数控旋压机的数控化改造，旋压力为20 t，产品精度达到了0.001 mm，满足了预期的要求。

[1] Hogan P，Burrows C R，Synchronizing Unevenly-loaded Hydraulic Cylinders，Fluid Power System and Technology[C]∥Proceedings of ASME International Mechanical Engineering Congress and Exposition，1994：75-80.

[2] 刘长年.液压伺服系统优化设计理论[M].北京：冶金工业出版社，1989.

[3] 杨博，李宛洲，王京春.工业重载液压系统的位置伺服控制[J].控制理论与应用，2010，27（1）：121-125.

[4] 裴喜永，原思聪.基于PID 控制的实验液压机电液伺服系统的仿真分析[J].煤矿机械，2010，31（4）：52-55.

[5] Turbo Pmac User Manual[Z].Deltatau Data Systems，Inc.2003.