直流调速系统与Matlab仿真

刘翔，曹萍，陈致远，冯天瑞，刘奇

（1.天津电气传动设计研究所有限公司，天津300180；2.河北工业大学电气学院，天津300130；3.天津市电力公司，天津300308）

1 引言

现今工控领域应用广泛的直流调速装置便是西门子直流调速装置系列中的6RA70，其容量范围为0.7～1 550 kW，额定电枢电流为15～2 000 A。电枢回路使用三相全控桥式电路，用于单象限工作装置的功率部分电路为一组单独的三相桥，而用于四象限工作装置的功率部分则为反并联三相桥。 励磁部分采用单相半控桥。

除了上述驱动回路外，6RA70 还拥有强大的控制单元，不但可以精确地完成基本的调速要求，同时还具有强大的拓展功能，以应对一些特殊复杂的工艺要求，也为调试人员带来极大的便利。然而，即使6RA70 功能如此强大，在实际调试过程中依然会遇到一些细节上的问题，最常见的便是利用装置自动优化功能，得到的速度环节PI值效果不理想。 通常调试人员的方法是设定一个经验值，然后看最后效果。 但是这个经验值设定多少，不同的调试人员会有不同的设定。 对于这个问题，希望通过Matlab 建立一套直流调速装置的仿真模型，利用模型计算出相应的PI 参数，为调试提供一个数学参考依据。

2 调速原理

6RA70 西门子直流调速装置采用双闭环控制系统，通过参数的设定，可以选择外环是速度反馈还是EMF 电压反馈。 而如今在大部分实际应用中，为了获得更高的调试精度，电机都会在主轴加装同轴编码器，以速度作为反馈值。 本文将结合某厂一套飞剪系统进行仿真，其采用电流速度双闭环。 以下仿真也是针对电流速度双闭环进行建模。

在直流调速双闭环系统中，电流环为内环，速度环为外环。 同时，为了获得良好的静态与动态特性，转速与电流两个调节器都采用PI 调节器。 此外，速度调节器成为调速系统的主导调节器，使得实际速度良好地跟随速度给定，同时由于PI 调节器的使用，稳态误差也将被大大减小；负载若有所波动，也可以被及时地调整；速度调节器的输出限幅还将决定电机所允许的最大电流。 而电流调节器作为内环调节器，在速度调节器工作的过程中，它将使实际电流紧紧跟随电流给定（也是速度环的输出量）；对于电网电压的波动，还可以起到抗扰动作用；当电动机过载或者堵转时，电流调节器的限幅限制了电枢电流的最大值，起到保护作用，一旦故障消失，整个系统又可以迅速恢复正常。

图1为双闭环调速系统结构框图。

图1 双闭环调速系统结构框图Fig.1 The structure block diagram of double closed loop speed regulation system

由图1中可以看出，在ASR 与ACR 之前分别有速度和电流2 个滤波环节，Ton，Toi为滤波时间常数。 ASR 与ACR 分别是转速调节器与电流调节器，采用PI 调节，以获得良好的静、动态特性。 通常会把电力电子变换器近似为Ks/(Tss+1)这样1 个一阶惯性环节，Ks由整流单元输出电压与整流单元控制电压的比值决定，Ts为装置平均失控时间，根据整流电路形式的不同，会有不同的取值。 整流单元之后是额定励磁下直流电动机的结构框图，它被分成3 个部分进行表示，Tm为电机惯性时间常数，Tl电磁惯性时间常数，R 为电枢回路总电阻，Ce为电动势系数。 α，β 分别为转速反馈系数与电流反馈系数。 由于电流转速的输入信号前有滤波，产生了延迟，因此为了使反馈信号与控制信号同步，反馈系数需要配置响应的延时。

需要指出的是，在实际应用中，为了补偿电流波动引起的电压波动，减小PI 调节器的调节量，从而提高系统的响应速度，6RA70 在电流环中加入了预控环节，减小了PI 调节器的调节量，大大提高了系统响应速度，但实际上，它对于PI参数的计算不产生任何影响，为了简化仿真模型，便于计算，模型中这部分将不予体现。

3 Matlab 仿真

3.1 数学模型的仿真

基于前面所分析的6RA70 直流调速装置，以图1为基础，建立数学仿真模型。 由于本飞剪系统在整个运行过程不进行弱磁调速，励磁始终为额定励磁。 图2为额定励磁时，直流调速系统的数学仿真模型。 参数选择结合某厂一台飞剪电机的真实参数进行设置。

图2 直流调速系统数学模型Fig.2 Mathematical model of DC speed control system

3.1.1 电机环节

此飞剪电机为直流电动机，额定电压UN=800 V，额定电流IN=2 513 A，额定转速nN=690 r/min，电枢回路电阻Ra=0.033 Ω，电感La=0.002 32 H，换算到电机侧的转动惯量J=1 150 kg·m2。电机模型的计算如下：

图1中电机环节的参数为：Tl=0.070 3 s，Tm=0.385 s，Ce=1.039。

3.1.2 整流环节

由于控制信号最大值为10，而电机额定电压为800 V，通过规格化可知整流环节增益为Ks=80；因为整流单元采用三相桥式整流电路，所以整流装置失控时间取经验值3.34 ms。

3.1.3 电流环节

在6RA70 装置的实际调试时，通常电流与转速的滤波环节设置为0，所以在建模时将滤波环节省去，与图1有所不同。 对于内环电流环，希望在无静差的同时又可以减小超调，因此选用Ⅰ型系统，但是由图2可以看到电动势作为一个扰动量会对传递函数的求解带来许多不便，由于速度环响应要比电流慢许多，在电流变化瞬间，速度是不变的，因此在计算传递函数时将其省略。 典型Ⅰ型系统参数求解公式如下：

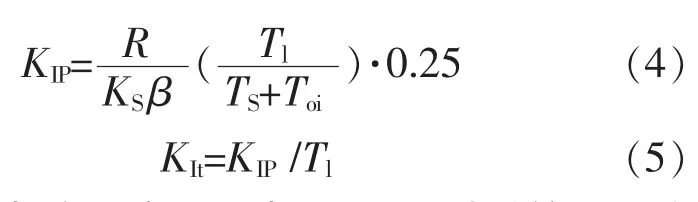
为了让电流环实现无超调，Ⅰ型系统KT 关系系数选择为0.25，结合参数求出电流调节器比例系数KIP=0.67，积分系数KIt=9.536，正负限幅设置为±10；电流反馈系数设置为0.003 98，反馈系数由给定的最大值与额定电流的比值来确定。

3.1.4 转速环节

电流环设计成为一个Ⅰ型系统，而速度环也拥有自己的PI 调节器，为了同样达到无静差，速度环将选用Ⅱ型系统，其参数求解公式如下：

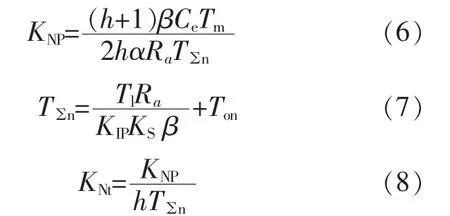
同时根据飞剪性能要求快速响应尽量减小超调，中频宽度h 选定为8，从而可求的速度调节器比例系数KNP=17.49，积分系数KNt=20.457，正负限幅设置为±10；速度反馈系数设置为0.014 5，反馈系数由给定的最大值与额定转速的比值来确定。

需要指出的是，由于Matlab 中的PI 调节器有自己特定的写入格式，上面电流转速2 个PI 调节器所设定的积分系数，并不是6RA70 中所设定的积分时间，而是比例系数与积分时间的比值。

根据图2建立模型，设定参数，进行仿真，仿真算法使用ode23tb，仿真时间15 s。 飞剪的运行特性要求转鼓在短时加速到最大速度，剪刃到达剪切位时，利用惯性剪切带钢，所以除剪切那一瞬间，其他时段近似于空载。 此时速度给定690 r/min，负载电流给定300 A （相当于空载运行电流）。 仿真结果如图3所示。

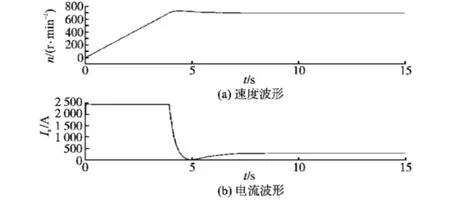
图3 直流调速系统数学模型仿真结果Fig.3 Simulation results of DC speed control system based on mathematical model

由图3可以看出这个系统在电流限幅100%时，3.6 s 完成速度升至690 r/min。 这套飞剪系统在实际应用中可允许300%的短时过载，换算后可知在3 倍过载的情况下，1.2 s 便可完成响应，符合工艺要求。

3.2 电路模型的仿真

Matlab 中为用户提供了强大的元件库，以便搭建与实际电路相接近的主电路。 在数学模型的基础上，运用SimPowerSystems 将数学模型中的整流环节和电机环节修改为电路模型，同时增添脉冲触发等环节，如图4所示。

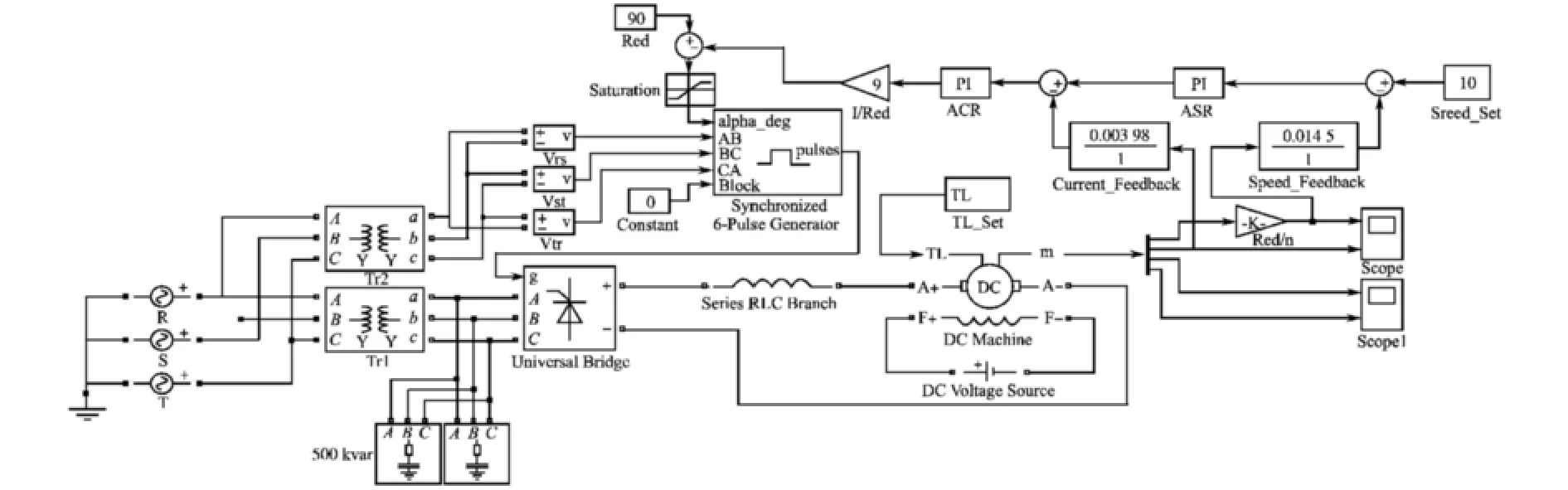
图4 直流调速系统电路模型Fig.4 Circuit model of DC speed control system

图4中首先设置10 kV 的三相工厂进线，再通过Y/Y 接法的整流变压器和同步变压器，将电压分别变压为800 V 与220 V，供三相整流回路与脉冲触发回路使用； 考虑到整流环节在工作时会使动力变压器二次侧波形产生畸变，所以需要根据电压与电流来设置阻容保护环节；整流回路将三相交流电压整流为电机所需的直流电压，通过的平波电抗器供直流电动机使用； 而脉冲触发环节即需要同步变压器提供电压的同步信号，同时还需要控制回路提供触发角的给定，由于控制原理相同，而控制回路由数学模型修改而来。

为了同数学模型仿真结果进行相应的比较，两个模型设定完全相同的参数进行仿真，仿真算法也使用ode23tb，仿真时间15 s，速度给定690 r/min，负载电流为300 A，仿真结果如图5所示。

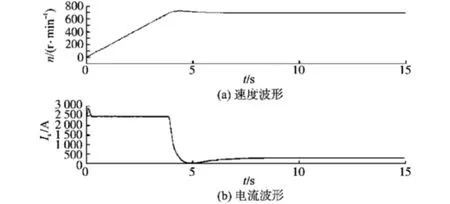
图5 直流调速系统电路模型仿真结果Fig.5 Simulation results of DC speed control system based on circuit model

由图5中可以看出，仿真结果与数学模型大体相同，响应时间3.6 s，稳态电流300 A。 但一些细节还是有所差别的，这是由于电路模型比数学模型更为复杂、真实所造成的。 比如，电流的超调要比数学模型中要大，这里主要有两方面原因：首先电机环节电路模型要比数学模型更为复杂，原先将电机近似模型化后算出的参数对于新的模型未必是最优的； 其次，整流环节同样也相应地复杂化，特别是在仿真开始的一瞬间，如同整流回路合闸，会有一瞬时的冲击电压，这也是造成电流超调偏大的原因。同时发现，在电路模型建立过程中，其实更加贴近现实，从而对电气设计与现场调试具有更加直观的指导意义。 例如，变压器与阻容保护的选定，直接影响到装置进线电压的品质，而平波电抗器的选择也会影响到电枢电压的品质等。 因此，仿真模型在帮助调试人员确定参数值的同时，也对选定的器件进行着校验。

4 现场的实际应用

6RA70 有着强大的自动优化功能，可以自动设置电流环节与速度环节的PI 参数，但是常年的实际应用发现电流环参数相对准确，速度环偏差较大。 所以众多工程调试人员在实际调试中舍弃自动优化出的速度环节参数，而保留了电流环节参数。

由于真实系统跟模型计算还是有不少差异的，诸如用于模型计算的参数本身就会与实际系统的参数存在误差；直流调速装置的程序中每一个功能块的运行也会占用一定时间。 所以在电流环节参数准确的前提下，为了减小电流环节模型与实际不同所引起的误差，笔者在现场调试时也保留了装置自动优化出的电流环节参数，并且使用电流环节优化出的数值带入式（7）。 进行计算后利用前面讲述的速度环节计算公式求得PI 调节器的比例系数与积分时间。

本飞剪系统自动优化出的电流环节PI 调节器参数为：比例系数PI=0.74，积分时间τI=0.086 s。将其带入速度环节PI 调节器计算公式可得：比例系数Pn=16.8，积分时间τn=0.111 s。经过一些调试改动，最终写入系统的速度环PI 调节器参数为：比例系数Pn=14，积分时间τn=0.1 s。 并且利用Trace 采集实际波形如图6、图7所示。

图6 实际飞剪系统启动到稳定运行波形Fig.6 Waveforms of the actual flying shear system from start to stable operation

图7 实际飞剪系统启动时波形Fig.7 Waveforms of the starting actual flying shear system

由图6可看出，启动时波形大体与仿真结果相仿。 同时通过图7可知，实际飞剪系统在电流限幅100%时1 s 内的加速为29.7%，从而可以推算出速度从0 加速到100%须用3.369 s，与仿真结果一致。 由结果可以看出，建立系统的模型后，通过计算得出的参数对实际现场调试具有指导意义，可以让调试人员得到一个相对准确的数值，在这个数值的基础上再进行相应的调整，既可以减少调整次数，缩短调试时间，又可以得到良好的调试效果。

同时针对不同的系统要求，中频宽度h 也是有不同的取值，h 的取值会直接影响速度环计算结果。h 减小，上升时间减少，超调增大，抗扰性能增强；h 增大，上升时间增大，超调减小，抗扰性能相对变差。 工程实践中证明h 在3～10 之间最佳。在现场，调试人员应根据不同实际情况进行相应的取值。

5 结论

本文首先介绍分析了6RA70 直流调速装置的双闭环调速的工作原理，后以此为基础运用Matlab 与实际系统参数对数学模型与电路模型分别进行了详尽的仿真，最后将两种模型仿真结果与实际波形进行了相应的对比。

利用建立的仿真模型，结合实际参数，可求出系统的所需参数，从而有的放矢的进行各个参数的调整，以期使得最终的调试结果尽善尽美。在仿真过程中，还可以对各个环节进行监控，来考量选用器件是否合乎标准。

在实际调试过程中，有些实验受限于机械、液压等条件不允许，也可以通过仿真来完成，以求出系统的极限参数，从而限定了参数范围，以免参数设置失当，造成不必要的损失。

[1] 陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社，2008.

[2] 顾春雷，陈忠.电力拖动自动控制系统与MATLAB 仿真[M].北京：清华大学出版社，2011.

[3] 董德智，孙驷洲.MATLAB 在双闭环直流调速控制系统教学中的应用[J].自动化与仪器仪表，2007（4）：40～43.