超低速PMSM系统的Modelica建模及控制参数整定

丁建完，梅再武，张学明

（1.华中科技大学 国家CAD 支撑软件工程技术研究中心，湖北 武汉430074；2.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033）

1 引言

随着电力电子技术、稀土永磁材料的飞速发展[1]，永磁同步电动机得到迅速推广。 因其体积小、效率高、功率因数高等优点[2]，永磁同步电机在数控机床、机器人、航空航天器等系统中具有广泛应用。 在某些应用领域，如卫星天线伺服系统，对永磁同步电机驱动系统的精度要求非常高，最低转速达0．001 （°）／s。 为提高这类超低速、 高精度永磁同步电机驱动系统的设计质量，缩短研发周期，降低成本，采用计算机仿真是一个很好的手段，因此研究超低速永磁同步电机系统的建模方法具有重要意义。

超低速永磁同步电机系统是一个涉及机、电、磁、控多个领域的强耦合、非线性系统，由于精度要求高，在对这类复杂系统进行建模时，必须保证模型的准确性，选用好的建模仿真分析方法。 目前较常用的建模仿真方法，如基于Matlab/Simulink 等，由于其本身是一种因果性联系的建模方法，注定了模块间计算过程数据流是单向的，因此，系统中某一模块的微小变动可能需要对整个系统模型进行较大修改，导致模型的可重用性不高。 而且，基于因果连接的建模方法，往往需要对实际系统的物理方程进行反演变形，对于非线性、强耦合系统模型，反演难度极大[3]。此外，基于因果连接的建模方法，也不适合处理涉及多个领域的复杂系统，难以建立完整的多领域系统模型。 基于Modelica 的多领域统一建模方法能很好地克服目前常用建模方法存在的不足。 Modelica 是一种面向对象、非因果关系的多领域统一建模语言[4-5]。 该语言支持多领域统一建模，具备模型重用性高、建模简单方便、无须符号处理等许多优点。

MWorks 是一个基于Modelica 的多领域统一建模仿真平台，本文在MWorks 平台上建立了超低速永磁同步电机系统的完整模型，实现了不同领域模型的无缝集成及系统的高置信度仿真。 在仿真分析过程中，采用蒙特卡洛随机试验的方法，对系统控制参数进行了整定，并分析了不同转速指令下控制参数的变化规律。 最后通过不同工况下的仿真，分析了系统精度、稳定性等各方面的性能。

2 超低速PMSM系统的Modelica建模

2.1 系统描述

超低速永磁同步电机系统对转速要求很高，其控制系统PI 参数需随转速指令的不同而作相应变化。 其次，由于转速极低，其负载力矩呈现出复杂的非线性特性，包含摩擦阻力矩，低频耦合力矩等。对此类高精度系统进行建模时，必须保证模型的精度，尽量贴近真实系统，确保模型有效。

本文研究的超低速永磁同步电机系统，其电机驱动控制系统采用基于转子磁场定向的矢量控制方案，控制系统结构如图1所示。 图1中，调节器REG1，REG2 为比例—积分调节器，REG3为比例调节器。 REG1 中比例积分系数固定，REG2，REG3 中的比例积分系数为可变参数，随转速变化而变化。

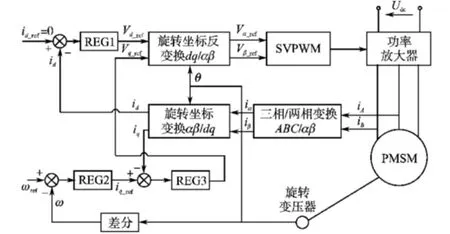
图1 基于转子磁场定向的矢量控制系统框图Fig.1 Vector control system block diagram based on rotor magnetic field oriented

电机负载力矩由3 部分叠加而成，分别是摩擦阻力矩、 耦合力矩及扰动力矩。 摩擦力矩随电机转速非线性变化，耦合力矩分量为频率极低的无偏置正弦力矩分量，扰动力矩包含100 Hz 及其倍频力矩分量。

2.2 系统建模

为保证模型的精度，本文从贴近真实系统的角度出发，基于Modelica 语言建立了超低速永磁同步电机系统的多领域耦合模型。 系统模型结构如图2所示。

图2 超低速永磁同步电机系统仿真模型结构Fig.2 The simulation model structure of ultra-low-speed permanent magnet synchronous motor system

系统模型主要由永磁同步电机模型、非线性负载模型、 旋转变压器模型、A/D 转换器模型、矢量控制算法模型、电压逆变器模型组成。 下面介绍其中主要模型的Modelica 实现方法。

2.2.1 永磁同步电机模型

永磁同步电机是一个高阶、非线性、强耦合的多变量系统，为简化永磁同步电机数学模型，作如下假设：1）忽略定、转子铁芯磁阻，不计涡流损耗和磁滞损耗；2）永磁材料的电导率为零，永磁体内部的磁导率与空气相同；3）转子上没有阻尼绕组； 4）永磁体产生的励磁磁场和三相绕组产生的电枢反应磁场在气隙中均为正弦分布；5）稳态运行时，相绕组中感应电动势波形为正弦波。

在以上假设的基础上，取转子永磁体基波励磁磁场轴线为d 轴，q 轴逆时针方向超前d 轴90°（电角度），可得到永磁同步电机在此坐标系下的数学模型为

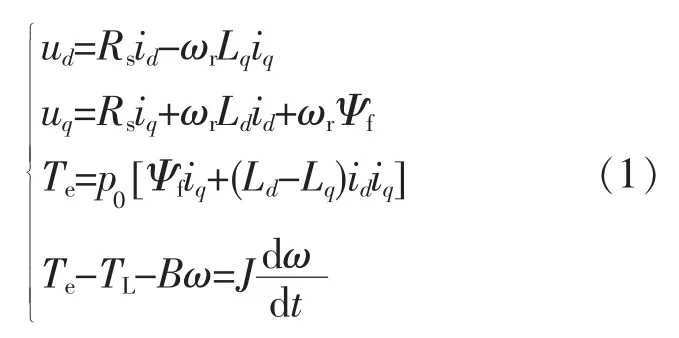
式中：ud，uq，id，iq分别为d，q 轴的电压和电流；Ld，Lq分别为d，q 轴的电感；Ψf为永磁体的主磁链；Rs为定子绕组的相电阻；ωr为转子角频率；p0为极对数；Te为电磁力矩；TL为负载力矩；B 为粘滞摩擦系数；ω 为电机机械角速度；J 为转子转动惯量。

本文根据永磁同步电机的等效电路，直接将上述永磁同步电机DAE 数学方程转化为Modelica 代码的方法构建了永磁同步电机模型。 模型结构和永磁同步电机等效电路如图3所示。

图3 永磁同步电机等效电路及Modelica 模型结构Fig.3 Permanent magnet synchronous motor equivalent circuit and the Modelica model structure

2.2.2 基于转子磁场定向矢量控制算法模型

Modelica 语言内在组件连接机制不仅支持非因果建模，同时也支持因果连接方式的建模。 建立基于转子磁场定向矢量控制系统模型时，与Matlab/Simulink 一样，采用基于组件之间的因果连接搭建。 首先建立基本的元件模型，然后根据图1所示的控制系统框图，连接各元件模型，组成了空间矢量控制算法模型。 模型图标及内部结构如图4所示。

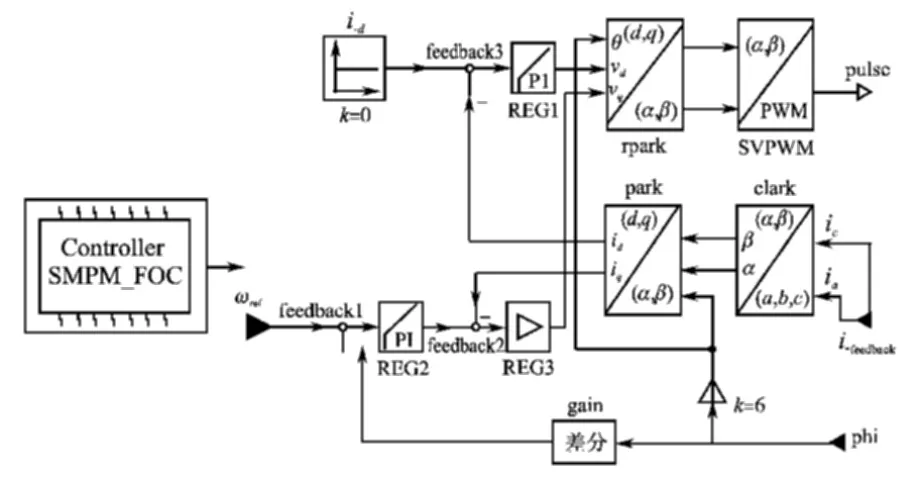
图4 矢量控制算法模型图标及内部结构Fig.4 Vector control algorithm model icon and the internal structure

图4中，比例—积分调节器REG2 和比例调节器REG3 中的比例、 积分系数为可变参数，可根据查表的方法确定。

2.2.3 非线性负载模型

由于超低速永磁同步电机伺服系统执行电机的转速极低，摩擦阻力矩具有很强的非线性，同时还必须考虑到耦合力矩及扰动力矩分量的影响。 建立负载模型时必须充分考虑到低速情况下负载的复杂性。 本文建立的负载模型由摩擦阻力矩、耦合力矩及扰动力矩3 部分组成。 为贴近真实情况，摩擦阻力矩模型中加入了幅值为0.2 N·m 的白噪声成分。耦合力矩分量为频率极低的无偏置正弦力矩成分，扰动力矩分量包含100 Hz，200 Hz，300 Hz 等100 Hz 的倍频成分，以及这些频率点附近的频率成分。 负载力矩模型图标及内部结构如图5所示。

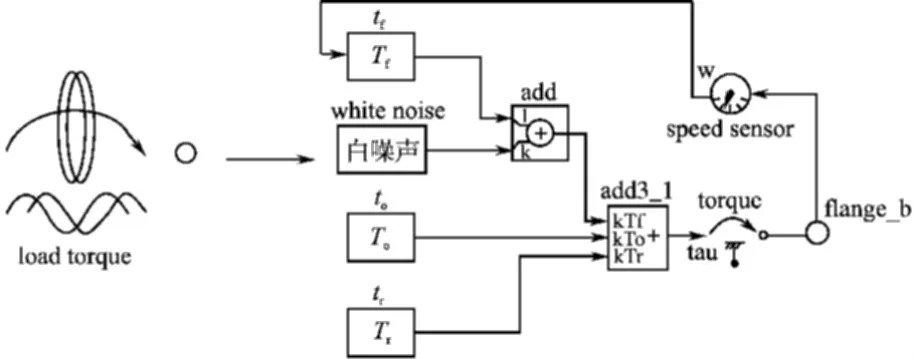
图5 非线性负载模型图标及内部结构Fig.5 Nonlinear load model icon and the internal structure

加入白噪声后的摩擦阻力矩随电机转速变化情况如图6所示。

图6 摩擦阻力矩与电机转速之间的关系曲线Fig.6 Relation curves between frictional torque and motor speed

2.2.4 电压逆变模型

电压逆变模型实现的是逆变器的功能，输入为空间矢量脉宽调制模块给出的6 路开关控制信号，输出为三相电压脉冲波。 建立逆变器模型时，可用基本的电气元件，如开关、二极管等，根据逆变器实际物理电路拓扑结构搭建。 模型结构如图7所示。

图7 电压逆变器模型结构Fig.7 Voltage inverter model structure

3 控制系统参数的整定

超低速永磁同步电机系统对电机的转速控制要求很高，转速变化时，控制系统参数也需要作相应修改，因此，研究控制系统参数整定方法与不同转速下控制参数的变化规律，是进行系统分析与设计很重要的一个方面。 目前工程上对控制参数的整定一般是依靠经验和技巧，在实物系统上进行调节，这种方法往往是繁琐、困难的。 本文通过多次仿真，采用蒙特卡洛随机试验的方法寻找匹配的控制参数，实现了控制系统参数的整定。 蒙特卡洛随机试验方法基本思想是让控制参数随机取值，通过软件自动进行多次仿真计算，在一定范围内寻找最合适的参数。 首先以均匀分布的随机初探方式，缩小最优控制参数的寻找区间，然后在所得区间中正态分布随机参数，以获得最优解。 方法流程图如图8所示。

图8 蒙特卡洛随机试验法调参流程图Fig.8 Scheduling flow chart of the Monte Carlo random test method

给定转速指令为3 （°）／s，以此为例，通过仿真试验同步调节控制系统的3 个PI 参数，3 个参数分别为励磁电流调节器的比例系数Kp2、 积分系数Ki2以及力矩电流调节器的比例系数Kp3。 控制目标为：准确跟踪转速指令、转速脉动小、超调量小、响应速度快。 首先让3 个参数以平均分布方式随机取值，进行样本容量为20 的仿真试验，试验结果如图9a 所示。

根据系统控制目标进行筛选，最优结果为：Kp2=8.215 61，Ki2=0.123 441，Kp3=7.527 7。

以上述最优结果为正态分布中心，标准差取15%，样本容量为20，进行仿真试验，试验结果如图9b 所示。

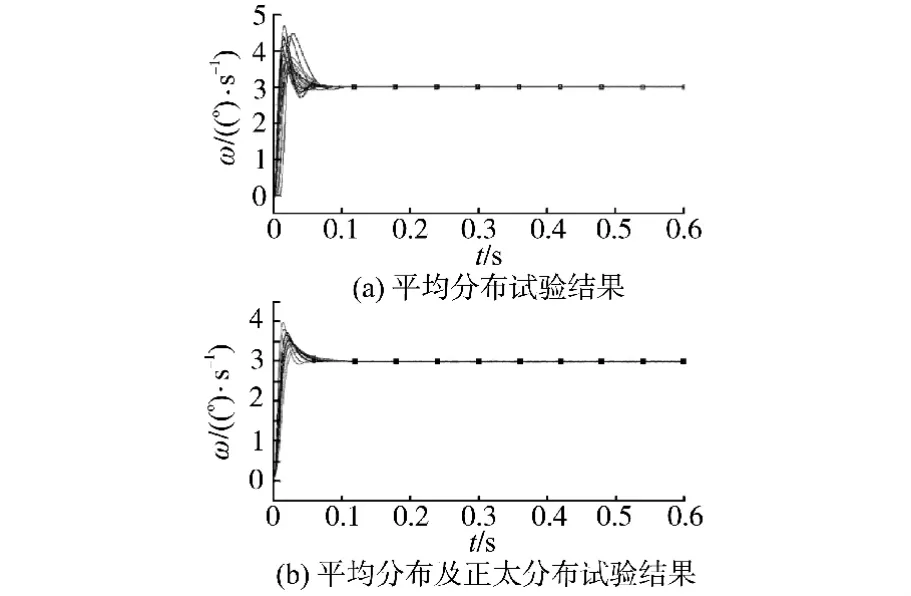
图9 样本容量为20 的平均分布及正态分布试验结果Fig.9 The average distribution and normal distributed test results for a sample size of 20

根据控制目标进行筛选，可得到最合适的控制参数为：Kp2=8.188 19，Ki2=0.077 659，Kp3=7.261 9。

对于每个不同的转速指令，都可以通过这种方法寻找满足控制目标最合适的控制参数。 通过大量仿真试验，可得到不同转速指令下控制参数的变化规律如图10所示。

图10 Kp2，Ki2，Kp3随转速增加变化曲线Fig.10 The variation curves of Kp2，Ki2，Kp3with the speed increase

4 仿真分析

系统模型建立后, 可在MWorks 上进行多种工况仿真，分析系统各方面的性能。 仿真过程中，PMSM 电机参数设置为：定子相绕组电阻Rs=1.275 Ω，dq 轴电感Lmd=Lmq=0.009 75 H，转子转动惯量J=0.05 kg·m2，额定频率f=324 Hz，极对数p=6。

4.1 不同转速指令下的仿真结果曲线

给定转速指令为1 （°）／s，电机转速响应曲线如图11所示。

图11 电机转速响应曲线Fig.11 Motor speed response curve

给定转速指令从-24 （°）／s 阶跃至24 （°）／s，电机转速响应曲线及三相电流曲线如图12所示。

图12 电机转速及定子绕组电压、电流曲线Fig.12 Motor speed and stator winding voltage and current curves

给定转速指令为正弦规律变化，幅值为20（°）／s，频率为10 Hz，电机实际转速与转速指令对比如图13所示。

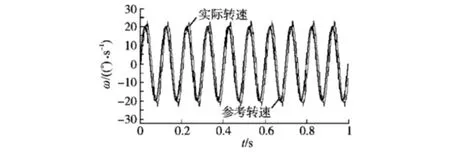
图13 电机实际转速与指令转速对比Fig.13 Comparison of the actual motor speed and instruction speed

从上述仿真结果中可看出，不论是在转速指令阶跃变化，还是按正弦规律变化，电机实际转速都能准确、快速地跟踪转速指令，转速控制精度高，动态响应快。 在较低转速指令1 （°）／s 下，超调量和稳定时间有所增加。

4.2 不同负载条件下的仿真结果曲线

给定转速指令为10 （°）／s，不断加大负载，电机转速曲线如图14所示，电磁力矩曲线如图15所示。

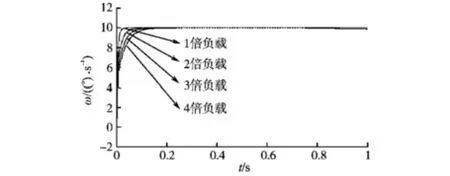
图14 不同负载条件下电机转速响应曲线Fig.14 Response curves of the motor speed under different load conditions

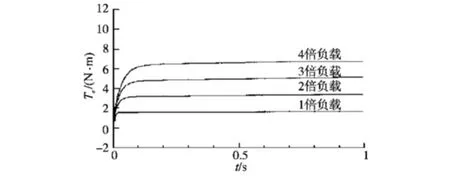
图15 不同负载条件下电机电磁力矩曲线Fig.15 The motor electromagnetic torque curves under different load conditions

进一步降低转速，给定转速指令为1 （°）／s，在不同负载条件下，电机转速响应曲线如图16所示。

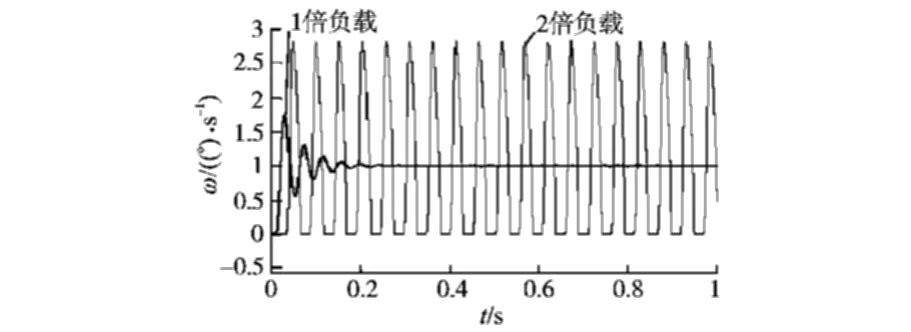
图16 不同负载条件下电机转速曲线(转速指令为1（°）/s）Fig.16 The motor speed curves under different load conditions (speed command is 1 （°）/s）

从仿真结果可以看出，转速指令为10 （°）／s时，负载按原负载成倍数增加，电机转速依然能准确跟踪转速指令，控制系统很稳定。 但是在较低转速1 （°）／s 下，负载大小对控制系统稳定性影响很大，负载增大一倍，电机转速便不能稳定。

5 结论

本文在充分分析超低速永磁同步电机系统特性的基础上，采用Modelica 语言陈述式基于方程的非因果建模方法，在MWorks 上搭建了超低速永磁同步电机系统的完整模型，并用蒙特卡洛随机试验的方法实现了控制系统参数的整定，分析了不同转速指令下控制系统参数的变化规律。仿真结果表明，波形符合理论，系统能平稳运行，具有较好的静、动态特性。 本文研究的方法应用于某型号卫星的姿态控制系统中，效果良好。 在进行系统建模与仿真研究过程中，可以得出如下结论。

1）基于方程的非因果建模方法能避免对实际物理系统的数学方程进行推导，极大地降低了复杂系统的建模难度，能满足超低速永磁同步电机系统的高精度建模与仿真。此外，Modelica 模型更加直观形象，可重用性强，稍加改变便能验证不同的控制算法，为分析和设计永磁同步电机伺服系统提供方便。

2）采用蒙特卡洛随机试验的方法调节控制系统的参数，理论简单，方法实用，对于工程中的控制系统参数整定具有一定的借鉴意义。

基于Modelica 的多领域建模方法，可在同一平台下实现不同领域模型的高置信度集成仿真。 在涉及多个领域的电机驱动系统时，使用该方法建模，能更好地进行系统的整体分析、设计与优化。

[1] Zhang Zhonghui，Shu Jiao.Matlab- based Permanent Magnet SynchronousMotorVectorControlSimulation[C]∥Proceedings of ICCSIT，2010:539-542.

[2] Sui Jun, Wang Jing，Fan Jian，et al.Application and Simulation of SVPWM in Permanent Magnet Synchronous Motor System[J].Ordnance Industry Automatio, 2011,30（3）:55-58.

[3] 陈琼忠，孟光.开关磁阻电机的Modelica 模块化建模方法[J].电机控制学报，2009,36（12）:1-5.

[4] 赵建军，丁建完，周凡利.Modelica 及其多领域统一建模与仿真机理[J].系统仿真学报，2006，18（2）: 570-573.

[5] Fritzon P.Principles of Object-oriented Modeling and Simulation with Modelica 2.1[M].New Jersey: Wiley-IEEE Press,2004.