逆时偏移中用Poynting矢量高效地提取角道集
王保利,高静怀,陈文超,张唤兰
1 西安交通大学电子与信息工程学院,西安 710049
2 中煤科工集团西安研究院,西安 710077
3 西安科技大学地质与环境学院,西安 710054
1 引 言
20世纪80年代就提出的逆时偏移[1-2]在对复杂地下结构进行成像时体现出了较强的优势,因此越来越受到人们的重视[3-10].多路径、多次波、大倾角、回转波、棱镜波以及保幅等关键问题上,逆时偏移几乎都可以较好地解决.但准确的逆时偏移成像比其它成像方法(如单程波偏移、Kirchhoff偏移和beam偏移等)对速度模型的准确度更加敏感.为了给逆时偏移建立一个较准确的速度模型,需要一种迭代的方法来不断地更新速度.而共成像点道集(CIGs)是叠前深度偏移中的很重要的输出道集,它可以提供速度建模所需要的信息,以及反映地下岩性的振幅和相位等信息.正确的速度模型得到的共成像点道集中的同相轴是平的,而不正确的速度得到的是弯曲的,且弯曲的程度与速度校正量是有关系的,通过这种关系就可以不断地更新速度模型[11].
通常,有两种共成像点道集,一种是偏移距域的(common-offset CIGs,简称为COCIGs),一种是角度域的(angle-domain CIGs,简称为 ADCIGs).在地下反射体是水平层状的情况,这两种道集是可互换的.Kirchhoff偏移和beam偏移方法可以很方便快速地输出COCIGs[12].但多路径问题会影响到COCIGs的质量,进而会影响速度分析和AVO分析的精度.而单程波偏移和逆时偏移中的COCIGs是很难提取的.Save和 Formel(2003)[13]利用单程波偏移在二维情况下首先提取了地下局部偏移距域的CIGs,然后再转换为 ADCIGs.Fomel(2004)[14]将这种方法推广到三维情况,并指出三维情况下该方法非常复杂.Save和 Fomel(2006)[15]又提出一种新的方法,该方法需要先生成延时CIGs,然后再转换为 ADCIGs.Xu等 (2010,2011)[16-17]提出一种直接从三维逆时偏移中提取ADCIGs的方法,该方法在频率波数域求取传播方向,进而计算出反射角和方位角信息,最后使用给定的成像条件直接输出ADCIGs.这种方法可以得到质量较好的ADCIGs,但需要保存所有时刻的炮点波场值和接收点波场值,并进行四维的傅里叶变换,计算量和存储量都非常得大,不适合进行逆时偏移速度分析等处理.
Yoon和 Marfurt(2003)[5]用坡印廷矢量来确定传播方向并用此修改成像条件来去除逆时偏移中的低频噪声,取得了较好的效果.本文借助于这种思想,用一阶应力速度方程(与常规标量应力波动方程相比,增加了额外的存储量,但减少了计算坡印廷矢量的耗时)进行波场延拓,并用坡印廷矢量求取成像点处的传播方向,最后使用给定的成像条件输出逆时偏移中的ADCIGs.
2 方法原理
2.1 波场传播
逆时偏移是通过波动方程在时间上对采集到的地震数据进行反向传播来实现的.其偏移过程使用的是双程波波动方程,因此不受倾角限制,且能正确地对回转波、多次波等进行成像.逆时偏移的原理本文不再赘述.
通常,逆时偏移采用的声波波动方程为标量应力波动方程[18-22,10],其形式如下:

其中,υ为介质纵波速度,P为质点应力波场.该波动方程不利于使用坡印廷矢量(原因见下节).因此本文采用一阶应力-速度声波波动方程:

式中:ρ为介质密度,υ为介质纵波速度,v和w 分别为x和z轴上的质点振动速度.本文对公式(2)采用交错网格技术[18]来构建波场传播算子.考虑到逆时偏移的计算量和为避免数值频散问题对逆时偏移结果的影响,在时间方向采用二阶而在空间方向采用高阶差分格式(≥8阶).
2.2 Poynting矢量求取反射角
坡印廷矢量也称为能流密度,1884年由坡印廷提出用来测量单位时间内穿过垂直于此矢量方向的单位表面的电磁场能量.Poynting矢量值等于电场强度与磁场强度的叉积,矢量方向代表电磁波的传播方向.
Yoon和 Marfurt(2003)[5]给出了地震波场中的坡印廷矢量计算式:
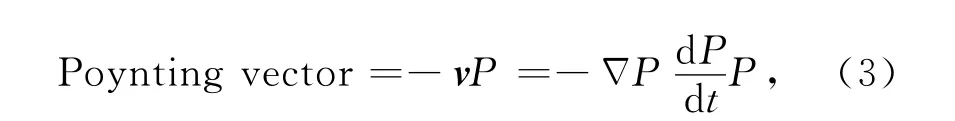
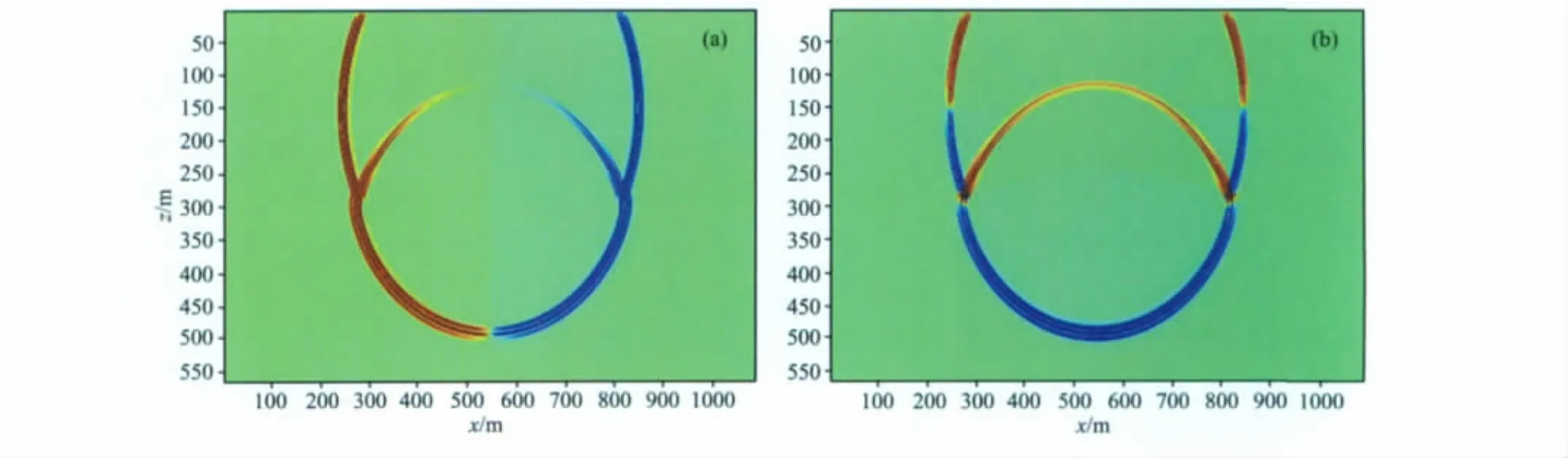
图1 坡印廷矢量快照图(a)水平分量;(b)垂直分量.Fig.1 The snapshots of Poynting vector(a)Horizontal component;(b)Vertical component.
其中,v表示位移速度矢量,v=(v,w),P为应力波场.通过(3)式可知,如果使用(1)式的标量声波波动方程,需计算应力波场值的时间和空间导数,计算比较复杂.而如果采用(2)式的一阶应力速度方程,则应力P和位移速度矢量v都是逆时偏移过程中已有的,不需任何额外计算.图1是均匀介质中的某时刻计算的坡印廷矢量快照图,可以很明显地判断出波的大致传播方向:在水平分量图(a)中蓝色和红色分别代表向右传和向左传,而在垂直分量图(b)中蓝色和红色则分别代表向下传和向上传.
用SS和SR分别表示炮点波场的坡印廷矢量和接收点波场的坡印廷矢量,则根据余弦定理,可以求出两矢量的夹角θ,
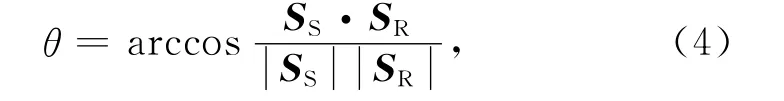
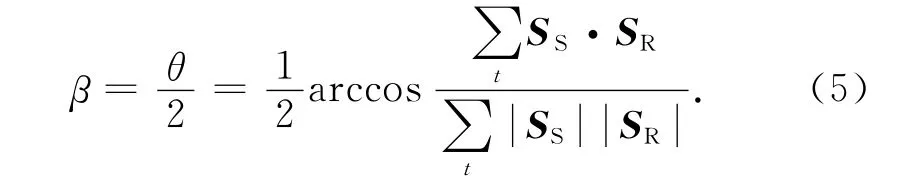
2.3 提取ADCIGs
获得反射角β后,便可以进行ADCIGs的提取.常规的逆时偏移成像条件是对所有角度道集的叠加,因此不能直接用来提取ADCIGs,需要进行修改.考虑到计算得到的反射角通常与我们给定的采样角度(一般是等间隔的)不一致,我们用高斯采样函数将常规的成像条件
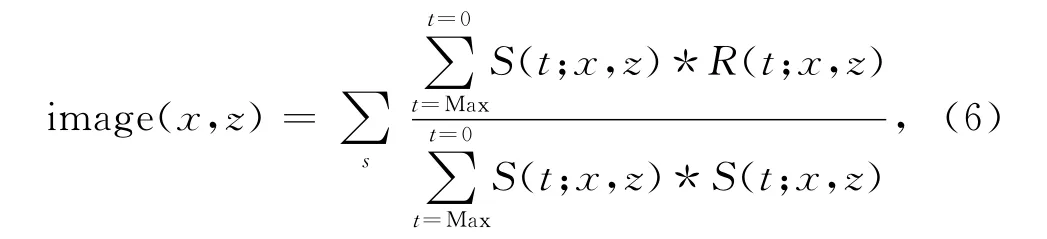
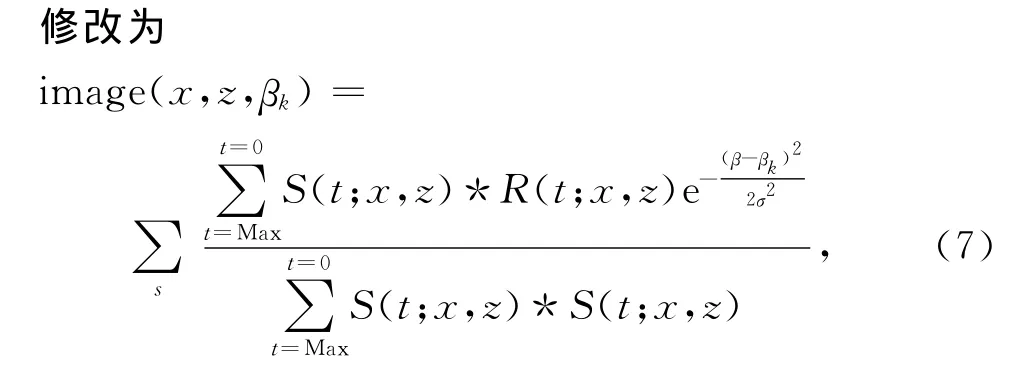
其中S和R分别表示炮点波场和接收点波场(本文中为应力波场值),而β表示当前时刻该成像点处计算得到的反射角,βk表示ADCIGs中的离散角,σ表示高斯函数的方差.根据(7)便能容易地提取出ADCGIs.
需特别说明的是,(5)式中,分母在很小甚至为零情况下,计算得到的角度β误差较大,但此时,其能量贡献也非常小,因此不会影响最终角道集的质量.
具体的计算流程如图2.
3 模型试验
3.1 Marmousi模型的ADCIGs
用本文提出的方法提取出的Marmousi模型的ADCIGs如图3所示.角度从0°~90°,角度间隔为2°,每100个CMP显示一个ADCIG,一共23个ADCIGs.从图上可以看出每个ADCIG上的同相轴都是拉平的,且低频噪声主要分布在大角度的道上.图4为第500个CMP位置处的ADCIG.
3.2 低频噪声
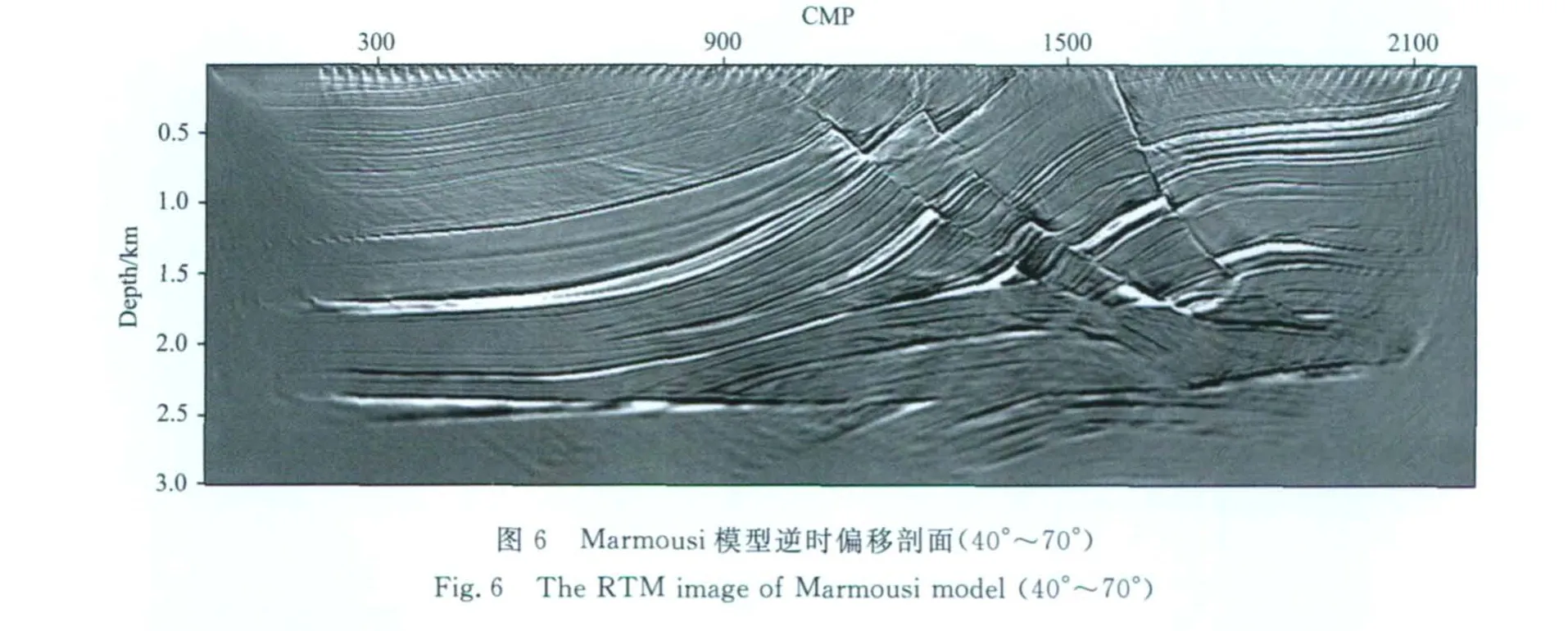
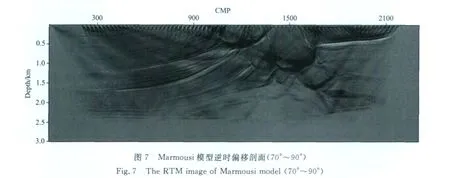
逆时偏移的低频噪声主要是由透射波成像造成的,而入射波和透射波的夹角在模型比较光滑情况下接近于180°(传播路径一微小段范围内),因此可通过在角道集上对大角度的道进行衰减或直接置零来对逆时偏移成像剖面进行去噪.理论上这种去噪方法等同于拉普拉斯滤波[7,11].图5、图6和图7分别为用0°~40°、40°~70°和70°~90°等角道集叠加后的结果,可明显看出在0°~40°内几乎没有任何低频噪声,而在70°~90°的偏移剖面几乎全部是低频噪声.
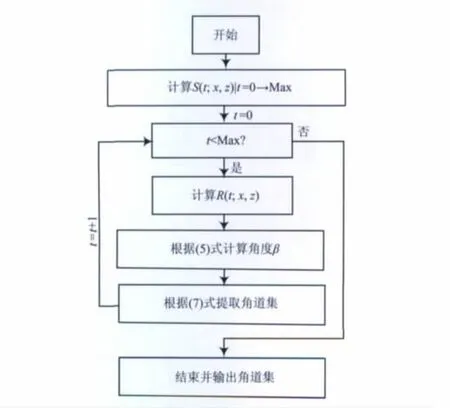
图2 Poynting矢量提取角道集的流程图Fig.2 The flow chart of extracting ADCIGs using Poynting vector


图4 Marmousi模型第500个CMP位置处的ADCIGFig.4 A ADCIG located at 500th CMP of Marmousi model

3.3 AVA
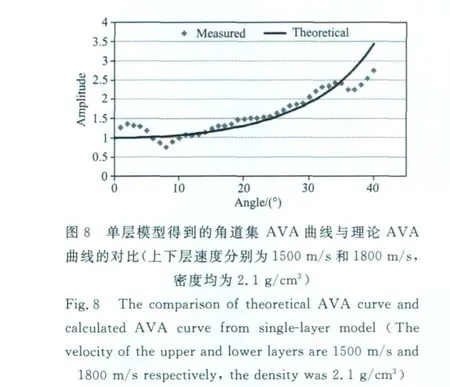
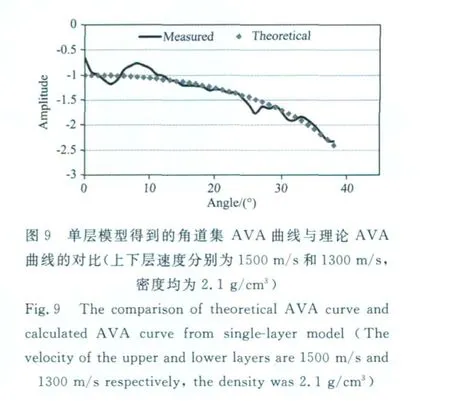
角道集的另一个用途就是用于AVA 分析[23-25],本文使用单层模型分析了角道集上振幅的特征.图8为用振幅随角度递增的模型参数(上下层速度分别为1500m/s和1800m/s,密度均为2.1g/cm3)得到的角道集AVA曲线与理论AVA曲线的对比.图9为用振幅随角度递减的模型参数(上下层速度分别为1500m/s和1300m/s,密度均为2.1g/cm3)得到的角道集AVA曲线与理论AVA曲线的对比.对比可以看出,两种模型得到的角道集的AVA曲线和理论AVA曲线基本一致.
4 实际数据试验
图10为从某地区的一条测线中提取出的部分ADCIGs.可以看出1.3~1.8km段中同相轴基本是平的,而在1.8~2.3km断层同相轴是向下弯曲的,说明偏移过程中所用的速度偏高.通过不断迭代地进行速度调整即可实现逆时偏移速度分析.

图10 实际数据中提取的部分角道集Fig.10 Part of the ADCIGs from field data
5 结 论
本文在逆时偏移过程中采用一阶应力速度波动方程进行波场传播,并用Poynting矢量来确定传播方向并计算反射角,进而通过给定的成像条件进行逆时偏移角道集的提取.整个计算过程中几乎不额外增加计算量和存储量,提取的共角度道集可用于进行速度分析和AVA分析等.该方法可用于三维逆时偏移中角道集等的提取(包括方位角道集),实现简单,易于进行并行加速(如GPU等).
后续工作将在此工作基础上,使用提取的角道集进行逆时偏移速度分析,以得到较好的偏移速度剖面.
(References)
[1]Whitmore N D.Iterative depth migration by backward time propagation.53rdAnnual International Meeting,SEG Expanded Abstracts,1983,2:827-830.
[2]Baysal E,Kosloff D D,Sherwood J W C.Reverse time migration.Geophysics,1983,48(11):1514-1524.
[3]张美根,王妙月.各向异性弹性波有限元叠前逆时偏移.地球物理学报,2001,44(5):711-719.Zhang M G Wang M Y.Prestack finite element reverse-time migration for anisotropic elastic waves.Chinese J.Geophys.(in Chinese),2001,44(5):711-719.
[4]Yoon K,Shin C,Hong S.3Dreverse-time migration using acoustic wave equation.An experience with the SEG/EAGE data set.The Leading Edge,2003,22(1):38-41.
[5]Yoon K,Marfurt Kurt J,Starr W.Challenges in reversetime migration.74thAnnual International Meeting,SEG Expanded Abstracts,2003:1057-1060.
[6]Bednar J B,Bednar C J,Shin C.Two-way versus one-way:A case study style comparison.76thAnnual International Meeting,SEG Expanded Abstracts,2006,25:2343-2347.
[7]Zhang Yu,Xu S,Bleistein N,et al.True-amplitude,angledomain,common-image gathers from one-way wave-equation migrations.Geophysics,2007,72(1):S49-S58.
[8]Zhang Y,James S. Practical issues of reverse time migration:True amplitude gathers,noise removal and harmonic-source encoding.First Break,2009,27(1):53-60.
[9]Liu F Q,Zhang G Q,Morton S A,et al.Reverse time migration using one way wavefield imaging condition.77thAnnual International Meeting,SEG Expanded Abstracts,2007,26(1):2170-2174
[10]Liu F Q,Zhang G Q,Morton S A,et al.An effective imaging condition for reverse-time migration using wavefield decomposition.Geophysics,2011,76(1):S29-S39.
[11]Zhou H B,Gray S H,Young J,et al.Tomographic residual curvature analysis:The process and its components.73rdAnnual International Meeting,SEG Expanded Abstracts,2003,22:666-669.
[12]Xu S,Chauris H,Lambaré G,et al.Common-angle migration:A strategy for imaging complex media.Geophysics,2001,66(6):1877-1894.
[13]Sava P C,Formel S.Angle-domain common-image gathers by wavefield continuation methods.Geophysics,2003,68(3):1065-1074.
[14]Fomel S.Theory of 3-D angle gathers in wave-equation imaging.74thAnnual International Meeting,SEG Expanded Abstracts,2004,1(1):1053-1056.
[15]Sava P,Formel S.Time-shift imaging condition in seismic migration.Geophysics,2006,71(6):S209-S217.
[16]Xu S,Zhang Y,Tang B.3Dcommon image gathers from Reverse time migration.80thAnnual International Meeting,SEG Expanded Abstracts,2010:3257-3260.
[17]Xu S,Zhang Y,Tang B.3Dangle gathers from Reverse time migration.Geophysics,2011,76(2):S77-S92.
[18]李博,刘国峰,刘洪.地震叠前时间偏移的一种图形处理器提速实现方法.地球物理学报,2009,52(1):245-252.Li B,Liu G F,Liu H.A method of using GPU to accelerate seismic pre-stack time migration.Chinese J.Geophys.(in Chinese),2009,52(1):245-252.
[19]李博,刘红伟,刘国峰等.地震叠前逆时偏移算法的CPU/GPU实施对策.地球物理学报,2010,53(12):2938-2943.Li B,Liu H W,Liu G F,et al.Computational strategy of seismic pre-stack reverse time migration on CPU/GPU.Chinese J.Geophys.(in Chinese),2010,53(12):2938-2943.
[20]刘红伟,李博,刘洪等.地震叠前逆时偏移高阶有限差分算法及 GPU实现.地球物理学报,2010,53(7):1725-1733.Liu H W,Li B,Liu H,et al.The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation.Chinese J.Geophys.(in Chinese),2010,53(7):1725-1733.
[21]刘红伟,刘洪,邹振等.地震叠前逆时偏移中的去噪与存储.地球物理学报,2010,53(9):2171-2180.Liu H W,Liu H,Zou Z,et al.The problems of denoise and storage in seismic reverse time migration.Chinese J.Geophys.(in Chinese),2010,53(7):2171-2180.
[22]刘红伟,刘洪,李博等.起伏地表叠前逆时偏移理论及GPU加速技术.地球物理学报,2011,54(7):1883-1892.Liu H W,Liu H,Li B,et al.Pre-stack reverse time migration for rugged topography and GPU acceleration technology.Chinese J.Geophys.(in Chinese),2011,54(7):1883-1892.
[23]杨午阳.模拟退火叠前AVA同步反演方法.地球物理学进展,2010,25(1):219-224.Yang W Y.Pre-stack simultaneous AVA inversion algorithm with simulated annealing.Progress in Geophys.(in Chinese),2010,25(1):219-224.
[24]王保利.弹性阻抗反演及应用研究.地球物理学进展,2005,20(1):89-92.Wang B L.Elastic impedance inversion and its application.Progress in Geophys.(in Chinese),2005,20(1):89-92.
[25]喻岳钰,杨长春,王彦飞等.叠前弹性阻抗反演及其在含气储层预测中的应用.地球物理学进展,2009,24(2):574-580.Yu Y Y,Yang C C,Wang Y F,et al.Application of prestack seismic elastic impedance inversion to gas reservoir.Progress in Geophys.(in Chinese),2009,24(2):574-580.

