基于压缩感知的随钻测井编码传输方法
张 煜,熊 轲,2,裘正定,王升辉
1 北京交通大学信息科学研究所现代信息科学与网络技术北京市重点实验室,北京 100044
2 清华大学电子工程系,北京 100084
1 引 言
随钻测井(M/LWD:Measurement/Logging While Drilling)是一种能在钻头钻进过程中测量、采集钻头附近测井数据,并将采集数据实时传输到地面系统的技术[1].测井数据通常包括地层特性信息和各种钻井工程参数.传统的测井技术为获取测井数据需要中断钻井过程,从井底吊出钻头,然后把测量设备下吊到井底以采集各种测井数据.这种方法操作步骤复杂,耗费时间长,得到的测井数据误差较大,很不利于地面施工人员实时精确控制钻井过程.相比传统测井技术,随钻测井由于在钻头钻进的同时采集测井数据并传送到地面工作站,使得地面施工人员能够实时了解井下地层状况和钻井情况,及时调整和优化钻井操作,从而大大提高钻井效率和成功率.由于上述优点,随钻测井系统已在石油开采、地质勘探[2]、岩层研究[3]等领域得到了广泛应用,随钻测井还可与其他技术如随钻地震[4-5]结合,用于地震监测等领域.国际工业界和学术界指出,随钻测井技术未来依然是国际测井技术发展和研究的重要技术[6].
尽管随钻测井技术已得到了广泛的应用,随着钻井技术的不断进步和井下所需采集与传输数据种类与信息量的不断增加,随钻测井正面临着许多严峻的技术挑战.如何及时可靠的传输测井数据是制约随钻测井技术发展的关键难题.通常钻井现场的施工环境都非常恶劣,要将各种传感器的测井数据从井底实时传输到地面是非常困难的事.为此,人们想了很多提高传输效率的办法,例如借助于电缆、光纤、特种钻杆、声波、电磁波以及钻井液等介质进行测井数据实时传输[7].由于技术和成本原因,目前使用最多的是电磁波和钻井液传输方式,其中电磁波方式由于信号衰减大仅在较浅的井使用,钻井液压力脉冲传输方式使用最为普遍.
在使用钻井液信道传输数据的随钻测井系统中,由于井底到地面的距离很长,而且信道环境异常恶劣,通常钻井液压力脉冲传输方式的传输速率仅为4~16比特/秒[8].加之,钻井液信道的噪声很强,微弱的脉冲信号几乎完全淹没在巨大的环境噪声中,所以钻井液信道的接收信噪比(SNR,signal to noise ratio)通常很低,这导致地面接收系统检测接收到的钻井液脉冲信号时常常伴随着较为严重的信道删除概率.据统计,钻井液信道的删除概率高达5%~10%左右,而且信道删除概率会随着钻井深度的加深继续增长.由于随钻测井钻井液信道属于低速率单向无反馈删除信道,地面系统通常无法向井下设备发送反馈信息,这意味着地面施工人员难以获得从井底实时上传的全部测井数据.
众所周知,要保证信息的正确传输,必须进行传输差错控制.传统的差错控制方法有两种.一种是利用纠错码检错并校正数据,这种方法需要在数据末尾增加额外的纠错比特位,会大大降低随钻测井系统的传输效率,因此不适合测井数据的实时传输.另一种是利用反馈重发机制,将错误数据重新发送,直到被正确接收.由于钻井液信道是一种单向无反馈信道,而且反馈重发会带来大量时间开销,因此反馈重发机制也不适用测井数据的实时传输.综上所述,考虑到数据传输实时性的需求,利用现有技术和方法很难矫正和恢复钻井液信道传输中测井数据的传输错误.现有的随钻测井系统采用了直接丢弃错误数据的方法,这会使得地面站所得的测井数据不完整,可能导致地面施工人员进行错误决策和错误钻井操作,给钻井工作带来了巨大的隐患.因此,如何在保证数据实时性的同时,提高数据传输准确率已成为随钻测井钻井液传输的重要研究问题和难题.
目前国内关于随钻测井技术的研究多集中于测井资料解释和测量仪器研究[9-15],对于钻井液信道传输系统中数据的正确传输关注较少.为此,本文提出了一种基于压缩感知理论(CS:Compressive Sensing)的信道编码传输方法——压缩感知信道编码(CSCC:Compressive Sensing Channel Coding)传输方法.该方法在井下采集端将需要传输的一组测井数据编码为一组压缩感知信道编码码元,然后通过钻井液信道向地面站传输.所有编码码元都具有均等的信息量并且每个码元都全部覆盖整个需要传输的信息域,因此对于地面站的解码端而言,只要接收到一定数量的正确码元就能恢复出全部原始测井数据,从而解决了在不可靠的无反馈删除信道中正确传输测井数据的问题.本文的主要创新工作与贡献有以下几点:
(1)首次将压缩感知理论应用并扩展到随钻测井系统,在保证数据传输实时性的同时,有效地提高了随钻测井传输的正确率.
(2)为增强传输性能满足随钻测井系统数据传输需求,本文针对不同数量测井数据和信道删除概率,提出了压缩感知信道编码的量化方法和编码方法.
(3)在上述工作基础上,利用实际油田随钻测井数据进行了实验验证,实验结果表明本文所提方法大大降低了由于信道传输错误带来的测井数据错误率.
(4)进一步分析比较了现有传输方法和本文所提方法的数据传输实时性性能和数据传输可靠性性能,结果表明本文所提方法在数据传输实时性和可靠性方面都大大优于现有方法.
本文各章节组织如下,第二节介绍了压缩感知理论框架和压缩感知特性.第三节介绍了将压缩感知理论引入测井数据实时传输领域遇到的问题和解决的办法.第四节提出了测井数据压缩感知信道编码的编解码方法.第五节通过真实测井数据实验,分析了在钻井液信道不同删除概率情况下测井数据压缩感知信道编码方法的性能,并与现有方法进行了比较.最后,第六节总结全文并给出结论.
2 压缩感知理论及特性
压缩感知理论是由Candes和Donoho等人在2004年提出的一种新的信息获取理论[16-20].压缩感知打破了传统的奈奎斯特采样定理,指出当信号具有稀疏性或可压缩性时,通过采集少量的信号测量值就可实现信号的准确或近似重构.压缩感知的主要目标是从少量的线性测量值中精确有效地重建信号,其核心在于试图从原理上降低对一个信号进行测量的成本.由于压缩感知具有重要的理论价值和广泛的应用前景,一经提出就得到了国内外研究者们的高度重视,被广泛的应用到通信、地球物理数据分析、计算机生物学、数据压缩、远程传感器网络等各个领域.
压缩感知理论框架的核心过程可表示为一个线性测量过程,描述如下:
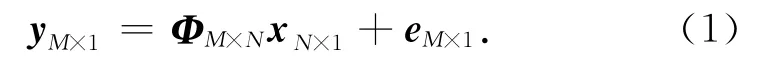
其中,xN×1为N维原始信号向量,且是K稀疏的.K稀疏是指xN×1满足其N个元素中至多只能包含K 个非零元素.yM×1为一个M维向量,通常称之为测量信号,可通过对xN×1采样得到.显然,M<N.eM×1为M 维向量,用于表示测量过程中的误差.ΦM×N是测量矩阵,用于描述采样系统特性.R代表解码端能从测量信号yM×1正确恢复原始信号xN×1所必需的测量值个数,也就是说只有解码端获得的测量值个数M大于R,解码端才能通过重构算法恢复原始信号.对于不同的重构算法,R的值也不同.R取值通常大于K但远小于N,即满足K<R≤M<N,且一般取值为Klog2N或2 Klog2N.这意味着,对于稀疏信号xN×1,只要测量值M≥R,就可通过重构算法从少量的M个测量值yM×1精确 (eM×1=0)或近似(eM×1≠0)恢复出 N维的xN×1.
尽管压缩感知具有上述优越性能,但从理论角度而言,压缩感知的使用必须满足一定应用条件.Candes和Tao[21]给出了压缩感知理论框架中测量矩阵的应用约束条件,即有限等距准则(RIP:restricted isometry property).文献[15]指出若对所有K稀疏的信号xN×1存在常数δ∈ (0,1)满足:
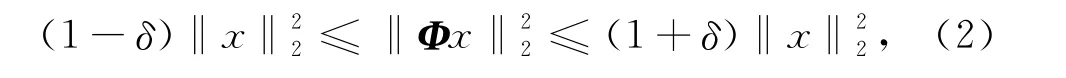
则保证通过重构算法能从(1)式得到的测量信号yM×1恢复出K稀疏的N 维信号xN×1.矩阵Φ满足(2)式,则称Φ满足K 阶有限等距准则.满足K阶有限等距准则的矩阵Φ即可作为(1)式中的测量矩阵.有限等距准则并不是一个非常严格的条件,现有研究已发现许多矩阵都满足有限等距准则,这极大提高了压缩感知技术的实用性和普遍性.常见的满足有限等距准则的矩阵有傅里叶矩阵(Fourier matrix)、非相干矩阵(Incoherent matrix)、二值矩阵(Binary matrix)、高斯矩阵(Gaussian matrix)以及贝努利矩阵(Bernoulli matrix)等等.
文献[22]进一步证明了有限等距准则另一个非常有用的性质,即如果一个矩阵Φ满足K阶有限等距准则那么由Φ的任意>R)个行向量组成的新矩阵Φ′也满足K阶有限等距准则.也就是说,只要新得到的矩阵Φ′的行向量个数超过R,就能用Φ′取代Φ 作为(1)式中的测量矩阵,(1)式变为
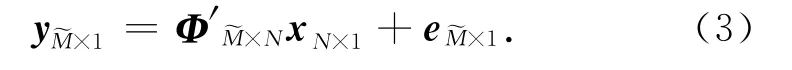
其中,Φ′~M×N是从原测量矩阵ΦM×N的M 个行向量中任选个行向量组成的新矩阵,通过重构算法可以从y~M×1恢复出xN×1.根据有限等距准则的这个性质,我们能利用任意>R)个测量值重构出原始信号xN×1.因为每个测量值带有关于原始信号xN×1同样多的信息量,对于重构算法来说每个测量值具有同样的重要性.
3 基于压缩感知的信道编码(CSCC)方法
利用压缩感知框架能根据任意不少于R个测量值重构出原始信号xN×1的特性,可以将压缩感知理论应用到随钻测井数据实时传输中,即CSCC.地面接收端依据正确接收到的部分测量值yH×1重构出井下传输的全部测井数据xN×1,从而提高实时传输数据的正确率.
3.1 CSCC基本原理
首先回顾在传统随钻测井系统中随钻测井数据实时传输过程:
在钻井开始前,地面施工人员选定本次钻井需要实时了解的若干种测井数据(如岩层密度,岩层自然伽马值,岩层电阻率等),然后设置井下传输设备实时传输选定的测井数据到地面系统.
钻井进行中,井下传输设备每次以帧为单位向地面系统传输数据,一帧包含每种选定的测井数据的一个数值.也就是说,井下传输设备每次传输的一个帧相当于(1)式中的xN×1,每种选定的测井数据数值作为向量xN×1的元素xi.例如,地面施工人员选择实时传输岩层密度,岩层自然伽马值和岩层电阻率三种参数.在钻井进行中,井下传输设备每次传输的向量xN×1维数则为3,并且x1是一个岩层密度数据,x2是一个岩层自然伽马值数据,x3是一个岩层电阻率数据.地面系统接收xN×1并将数据解释为相应测井数据.若传输过程中x2出错,则此次地面系统只能获得x1和x3的数据.
在引入压缩感知信道编码的传输系统中,井下传输设备通过(1)式对将要传输的若干个测井数据组成的向量xN×1进行CSCC编码处理,将xN×1转化为测量值向量即(1)式中的yM×1.根据现场具体情况选择G个测量值向地面传输,以帧为单位向地面传输yG×1,每帧包含G个测量值数据.由于信道存在删除概率,地面接收端接收到一部分正确的测量值yH×1和一部分错误的测量值.只要获取的正确测量值数量达到压缩感知重构算法的要求R,地面接收端就能重构出井下传输的全部测井数据xN×1.从而实现在不可靠信道中正确传输全部测井数据的目的.
根据压缩感知性质,地面系统接收到至少R个正确的测量值yi就能成功重构出原始信号,因此可以得到地面系统成功重构原始信号的概率如下:
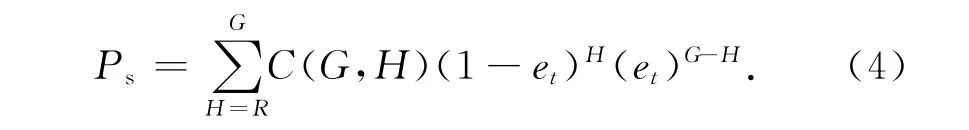
其中,Ps为地面系统成功重构原始信号的概率,et为信道删除概率,C是组合计算函数,G为井下传输设备一帧传输的测量值个数,H为地面系统接收一帧数据后正确接收到的测量值个数.显然H≤G,当H≥R时地面系统能成功重构原始信号.根据(4)式,每帧传输的测量值越多,地面系统成功重构原始信号的概率越大.根据信道删除概率et调节每帧传输的测量值个数G,容易使Ps达到预期的数据传输正确率.因此,利用压缩感知技术,可以提高在单向无反馈低信噪比删除信道中数据的传输正确率.
上面给出了CSCC的基本原理和特性,然而在将压缩感知理论扩展到测井数据实时传输之前,必须要解决几个问题,使CSCC与实时测井数据传输相适应.首先要对实时测井数据进行预处理,将它转变成与压缩感知编码框架相适应的形式.其次,在应用压缩感知编码框架式(1)将测井数据xN×1转变成测量值yM×1时,引入了测量误差即式(1)中eM×1.必须采取措施消除测量误差保证地面系统能精确重构出原始信号.最后,在地面解码端重构信号时,必须解决从原始测量矩阵ΦM×N中获得新测量矩阵Φ′H×N的问题.下面逐一解决这些问题.
3.2 信号预处理
为了提高CSCC编码性能,在利用式(1)得到测量值yM×1之前要对原始测井数据xN×1进行信号预处理,使xN×1便于后续的压缩感知编码处理.信号预处理包括移除奇异值和压缩原始测井数据.
3.2.1 奇异值滤除
由于受到井下恶劣工作环境干扰,随钻测井井下仪器有时会产生大大偏离正常范围的测井数据,这些不准确的原始测井数据称为奇异值.奇异值不仅对地面施工人员进行测井分析没有参考价值,它的存在还会干扰地面施工人员的判断.更为严重的是由于奇异值普遍偏大,它会使压缩感知框架中测量值的量化溢出率大大增加,从而影响编码效果.因此,在编码前必须去除原始测井数据中的奇异值.
本文采用电子测量中常用的3δ准则来剔除奇异值.3δ准则广泛应用于测量误差的处理,主要功能是挑出测量中的粗大误差,可有效地将信号突变区分出来.假设井下仪器获得的某种测井数据g的数据序列为g1,g2,g3,…,¯g为测井数据g的平均值,δ为标准差,如果>3δ,则认为gi为奇异值,这时可将gi剔除使用下一个正常数值gi+1作为测井数据向量xN×1的元素.
图1a为原始岩层自然伽马值测井数据曲线,图1b为剔除奇异值后岩层自然伽马值测井数据曲线.比较图1a和图1b可以看出,测井仪器受到干扰而得到的不准确的测井数据被有效剔除.
3.2.2 测井数据压缩
通过分析压缩感知框架式(1),测量值向量yM×1的元素yi是对原始测井数据xN×1的线性求和,因此yi的值明显大于xi的值.通常必须用比表示xi多一倍的比特数来表示yi,这意味着利用压缩感知框架将原始测井数据向量xN×1转变成测量值向量yM×1来存储或传输,可能要存储或传输更多的比特数.但是实际随钻测井系统有限的传输带宽要求井下设备传输尽可能少的比特数来满足测井数据传输实时性的要求.因此在使用压缩感知框架处理原始测井数据向量之前,必须采取措施降低原始测井数据的比特数从而降低变换后测量值的比特数.
为降低原始测井数据比特数,本文选择Differential Pulse Code Modulation(DPCM)数据压缩技术将原始数据xN×1压缩为~xN×1.DPCM 技术只是数据预处理手段,也可以选择其他的数据压缩技术,并不影响后续处理.我们之前的工作[17]提出了采用DPCM压缩实时测井数据,可在保证不影响地面施工人员测井分析的前提下将原始测井数据压缩为原来的一半.本文利用DPCM将原始数据xN×1压缩为~xN×1后,再使用测量矩阵对~xN×1进行测量得到测量值向量yM×1,此时可用与原始数据xN×1相同甚至更少的比特来表示yM×1,满足测井数据传输实时性的要求.在随钻测井系统中实时测井数据xi通常用8比特或12比特表示.以8比特的原始测井数据xi为例,利用DPCM将它压缩为3比特或4比特的~xi,对~xN×1进行测量得到测量值向量yM×1.根据~xN×1的稀疏性仅用6比特或7比特就可以表示测量值向量yM×1.关于采用DPCM压缩实时测井数据的更多细节见文献[23].
在此声明本文余下部分提到的原始数据xN×1都是指经过预处理的实时测井数据.
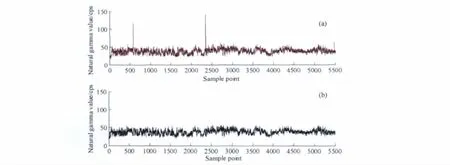
图1 原始测井数据曲线(a)与去除奇异值后(b)的测井曲线对比Fig.1 Curves of the original log data(a)and after removal of logs singular value(b)
3.2.3 测量误差消除
在压缩感知理论框架式(1)中,测量值的误差eM×1会直接影响重构原始信号xN×1的精确性.为保证地面系统重构原始信号的精确性,井下编码端在向地面传输测量值向量yG×1之前必须先消除使用压缩感知框架测量过程中引入的误差eM×1.
首先分析测井数据压缩感知信道编码过程中测量误差eM×1的产生原因.在随钻测井系统中,必须用有限的n比特表示测量值向量yM×1的元素yi.量化yi的过程会带来量化误差和溢出误差.这两部分误差构成了本文式(1)中的eM×1.
下面采用不同措施消除测量误差eM×1的两个成分,量化误差和溢出误差.
量化误差是指量化结果和被量化的yi间的差值,量化级数越多,量化的相对误差会越小,若量化步长与被量化的yi的单位间隔相等则量化误差为零.根据前文所述,随钻测井系统中的原始测井数据都是由若干比特表示的,因此可以把原始测井数据看作整数对待.为消除量化误差,本文选用贝努利矩阵作为压缩感知框架中的测量矩阵ΦM×N.贝努利矩阵是一种矩阵元素随机取值为+1或-1的矩阵,因此通过贝努利矩阵测量原始测井数据得到的测量值yi也是整数形式,只要量化步长为1则量化误差为零.本文采用线性均匀量化策略量化整数测量值yi,量化单位为整数1,因此本文量化策略不会引入量化误差,eM×1只由溢出误差构成.
溢出误差是指当测量值yi超出有限的n比特能表示的量化范围时,测量值与量化结果的误差.n比特线性均匀量化策略的无误差量化范围是[0,2n-1]的整数,超出此范围的测量值都会产生溢出误差.显然测量值的溢出误差越小越有利于地面解码端精确重构出原始信号.
定义:称量化产生溢出误差的测量值数量与量化的测量值总数的比值为测量值溢出率.
利用测量值溢出率可以衡量测量值溢出误差对地面解码端重构信号精确性的影响.显然,测量值溢出率越低,表示eM×1越小,越有利于地面解码端精确重构信号;测量值溢出率越高,表示eM×1越大,越不利于地面解码端精确重构信号.
有三种常用的方式能降低测量值溢出率.最简单的方式是增加量化测量值的比特数,通过扩大量化范围使全部测量值落在可量化范围内来降低溢出率.但是对于随钻测井系统来说,增加量化比特数降低溢出误差的方式效率太低.因为在溢出率很高时,增加量化比特数能有效地降低溢出率.但是随着溢出率降低,增加量化比特数降低溢出率的效率也随之降低,当溢出率较低时增加量化比特数效果相当有限.而且这种做法会大大降低随钻测井系统的传输效率,因为当溢出率较低时大部分的测量值可以用较少的比特数量化,系统必须传输大量的冗余比特,不利于测井数据的实时传输.第二种方式是增加量化间隔来扩大量化范围降低溢出率,但这种方式会引入量化误差,同样会影响测量值的准确性从而导致重构得到的原始信号的误差.最后一种方式是直接抛弃产生溢出误差的测量值而只传输没有溢出误差的测量值,也就是只传输[0,2n-1]范围内的测量值.这样在有限比特位均匀量化条件下,井下传输的测量值都没有因量化操作引入误差,即eG×1=0.
本文采用第三种方式,即直接抛弃产生溢出误差的测量值而只传输G个没有溢出误差的测量值,此时井下发送端压缩感知框架式变为
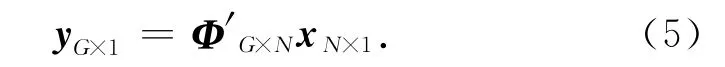
比较(1)式和(5)式,容易分析得出,M 必须远远大于G(根据真实测井数据编码实验效果,本文设置M为G的两倍到三倍),这样才能保证井下编码发送端有足够的备选测量值选出G个没有溢出误差的测量值构成yG×1.
3.2.4 新测量矩阵Φ′H×N的获得
设地面解码接收端通过钻井液信道接收yG×1获得的正确测量值为H维向量yH×1.由于信道的传输错误,yH×1由yG×1的部分元素组成.地面解码接收端必须获得yH×1和Φ′H×N才能重构出信号xN×1,但地面解码接收端只有ΦM×N无法直接获得Φ′H×N.因此地面解码接收端在进行信号重构之前必须从ΦM×N中找出与yH×1对应的行向量组成Φ′H×N.
根据式(1)、式(5)及上面的分析,能得出测量值向量y从井下测量产生,量化传输到地面接收的演变过程:
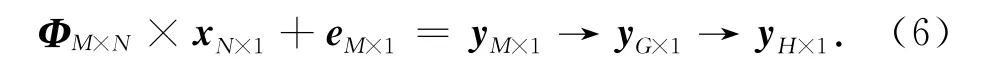
下面具体分析yM×1、yG×1及yH×1与 ΦM×N的关系.yM×1是井下编码发送端使用测量矩阵ΦM×N对原始测井数据xN×1进行测量得到的测量值向量,因此yM×1的元素yi与ΦM×N的行向量Φi一一对应.根据上一节的分析,井下编码发送端从yM×1中选出G个精确量化的测量值组成yG×1并由钻井液信道向地面系统传输.因此yG×1由yM×1的部分元素组成,显然yG×1的元素与ΦM×N的行向量不是一一对应的.也就是说yG×1的第一个元素y1可能不是由ΦM×N的第一个行向量Φ1与xN×1计算得到的,而是yM×1中第一个没有溢出误差的测量值yi.yH×1是地面解码接收端通过钻井液信道接收yG×1获得的正确测量值组成的H维向量,yH×1由yG×1的部分元素组成.因此yH×1的元素与ΦM×N的行向量也不是一一对应的.测量矩阵ΦM×N对地面解码接收端和井下编码发送端来说都是已知的,但地面解码接收端根据ΦM×N和yH×1无法重构出原始信号xN×1,因为yH×1与ΦM×N不匹配.因此地面解码接收端必须从ΦM×N中获得与yH×1匹配的Φ′H×N才能成功的重构出原始信号xN×1.
为使地面解码接收端能够获得与yH×1匹配的Φ′H×N,本文为yM×1的每个元素yi增加一个序列号i.地面解码接收端根据每个测量值yi的序列号i能很方便的找到ΦM×N中与yi对应的行向量Φi,将yH×1的H个元素yi对应的H 个行向量Φi组合起来就得到了Φ′H×N.如果直接用s比特表示序列号i,s必须满足2s-1≥M才能完全表示出M 个测量值的序列号.而且s会随着选取的测井数据种类增加而增大,当选择的实时传输测井数据种类较多时s也会较大,不利于数据的实时传输.例如,当地面施工人员选择8种测井数据实时传输时,即N=R=8.根据M>G>N=R,取G=10,M=20,此时s=5.意味着必须用5比特来表示序列号,而测量值数据本身仅用6比特或7比特来表示,序列号几乎占用了一半的传输带宽,大大降低了测井数据实时传输效率.
为克服直接用s比特表示序列号带来的测井数据实时传输效率大幅降低的问题,本文设计井下仪器采用固定的2或3比特传输测量值序列号的余数,地面系统根据得到的序列号余数恢复出原始的序列号.
下面以2比特表示测量值序列号余数说明本文方法.井下编码发送端用2比特表示测量值序列号i对22的余数0,1,2,3四个数字而不是直接表示序列号i,也就是说要把序列号i转化为序列号i对22的余数i mod 4(x mod y表示x对y取余数).地面解码接收端再将余数i mod 4恢复成测量值序列号i并从ΦM×N中获得Φ′H×N进行原始信号重构.显然序列号编码i mod 4与i不是一一对应的,所以当井下编码发送端采用i mod 4表示i时,地面解码接收端可能无法将i mod 4恢复成测量值序列号i.分析发现,只要测量值溢出和信道删除不造成连续22个测 量 值 丢 弃 (如 连 续 丢 弃 测 量 值 yi-1,yi,yi+1,yi+2),地面解码接收端就能准确的将i mod 4恢复成测量值序列号i.例如,由于测量值溢出和信道删除,地面解码接收端只接收到测量值y1,y2,y6,y8,y9和序列号编码1,2,2,0,1.由于没有发生连续4个测量值丢失,地面解码接收端能根据序列号编码1,2,2,0,1恢复出序列号1,2,6,8,9.而如果地面 解 码 接 收 端 接 收 到 测 量 值 y1,y2,y7,y8,y9和序列号编码1,2,3,0,1,则地面解码接收端根据序列号编码1,2,3,0,1恢复出的序列号为1,2,3,4,5而不是1,2,7,8,9,因为地面解码接收端丢失了4个连续的测量值y3,y4,y5,y6.在这种情况下地面解码接收端无法正确找到与yH×1对应的Φ′H×N,从而无法正确重构出原始信号.为确保正确重构出原始信号,根据测量值溢出率和信道删除概率情况,选择2或3比特来表示测量值序列号.当测量值溢出率和信道删除概率较小时,采用2比特表示测量值序列号,提高数据传输效率.当测量值溢出率和信道删除概率较大时,采用3比特来表示测量值序列号,避免地面解码接收端无法正确恢复原始测量值序列号.
4 实时测井数据压缩感知信道编解码
文献[23]中的实时数据编码方式不能保证通过删除信道地面系统还能正确接收到全部的实时测井数据.因此,本节在上一节分析的基础上,提出一种新的实时信道编码方式来改进文献[23]中的实时数据编码方式,保证在存在一定信道删除概率时地面系统能正确接收到井下设备传输的全部实时测井数据.
在传统的随钻测井系统中,如果地面施工人员选择了N种测井参数实时传输,井下传输设备每次必须传输N维的原始测井数据向量xN×1.本文利用压缩感知框架对测井数据xN×1进行编码,得到M维有误差的测量值向量yM×1,从中选取无误差的测量数据组成向量yG×1.井下传输设备每次通过钻井液信道传输G维的向量yG×1.由于存在信道删除概率,地面系统接收到H(H≤G)个正确传输的测量值yi组成的向量yH×1,只要接收到的正确测量值个数大于R(H≥R),地面系统就能准确的重构出原始测井数据xN×1.
在使用压缩感知框架编码前,需要对经典的压缩感知框架进行一些调整,使它与实时测井数据传输相适应,压缩感知算法对调整后的框架仍然有效.在井下编码发送端压缩感知框架中,测量矩阵ΦM×N是一个M×N(M>N=R>K)的矩阵,与经典压缩感知框架中测量矩阵ΦM×N是一个M×N(K<R≤M<N)的矩阵有所不同.因为实际原始测井数据向量xN×1的元素xi通常不为零,xN×1的稀疏度K通常很接近N,即K≈N.结合式(1)的条件K<R≤M<N,本文中取精确重构原始信号所必需的测量值个数R等于N.根据前面的分析,在测井数据实时传输压缩感知框架中,为克服溢出错误M必须大于G,为克服信道传输错误G必须大于R,故M>N.
下面分别介绍井下编码发送端和地面解码接收端的处理过程.
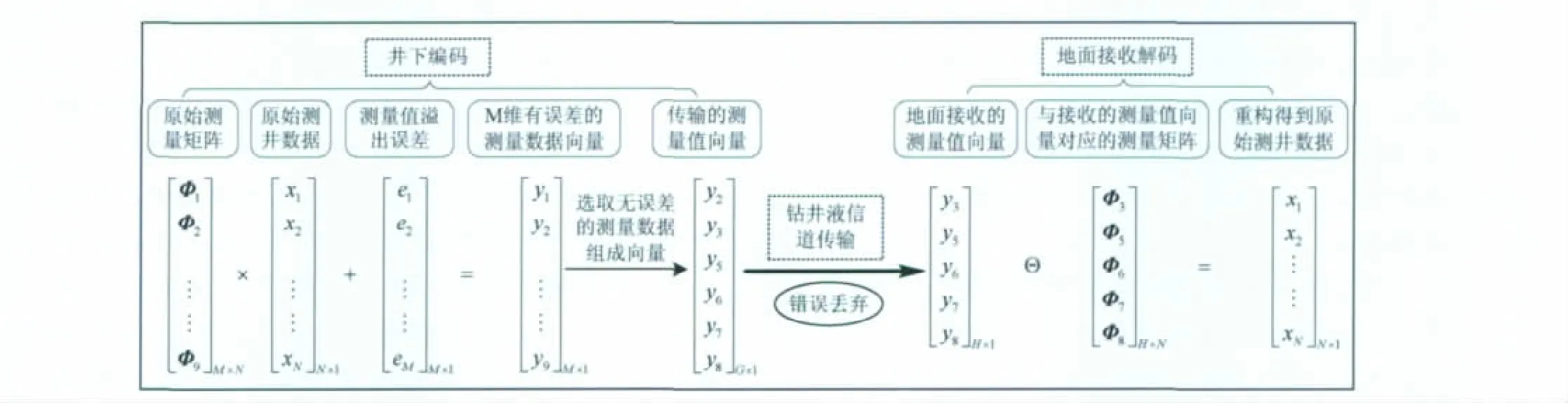
图2 利用CCSC的实时测井数据编码解码过程Fig.2 Real-time encoding and decoding process of logging data using CSCC
井下编码发送端的压缩感知框架为xN×1是N维向量,元素是经过预处理的原始测井数据.ΦM×N是原始测量矩阵,对井下编码发送端与地面解码接收端来说ΦM×N是已知的.eM×1为测量xN×1过程中的误差,本文中指量化yM×1过程中引入的误差.井下传输设备每次向地面传输G维的测量值向量yG×1,yG×1的每个元素都是精确量化的测量值,也就是说yG×1的每个元素都没有在量化过程中引入误差,保证地面解码接收端能精确地重构原始信号.
由于信道删除概率,地面解码接收端只能从井下编码发送端发送的G个测量值中接收到H 个正确的测量值(yG×1→yH×1),显然H ≤G.因此地面解码接收端的压缩感知重构框架为
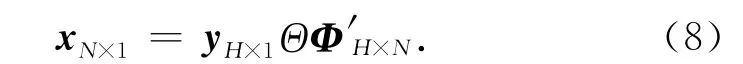
xN×1是N维向量,元素是经过预处理的原始测井数据.Φ′H×N是地面解码接收端压缩感知框架中的测量矩阵,Φ′H×N由ΦM×N中与接收到的H 个正确的测量值对应的行向量组成.yH×1是地面解码接收端接收到的H个正确的测量值组成的H 维向量.如果H≥R,地面解码接收端能利用重构算法(如文献[24]所述迭代重构算法)根据式(8)重构出xN×1,其中Θ代表重构算法的迭代运算过程.如果H<R,地面解码接收端不能重构出xN×1,测井数据本次实时传输失败.
下面以图2为例说明整个编码解码过程.假设施工人员选择了5种实时传输的测井数据(N=5),xN×1由5种测井数据组成.地面解码接收端至少需要接收到5个正确的测量值(R=5)才能正确的重构出xN×1.根据测量值溢出率和信道删除概率情况,选择M=9、G=6用2比特表示测量值序列号.首先井下编码发送端通过测量矩阵ΦM×N对原始测井数据xN×1进行测量,得到的一个9维的测量值向量yM×1.然后丢弃yM×1中存在溢出误差的测量值y1和y4,剩下7个无溢出误差的测量值 (y2,y3,y5,y6,y7,y8,y9).井下编码发送端在剩下的7个无溢出误差的测量值中,按先后顺序选择前6个无溢出误差的测量值 (y2,y3,y5,y6,y7,y8)和对应的序列号编码(2,3,1,2,3,0)组成6维的测量值向量yG×1,并将yG×1通过钻井液信道发送给地面解码接收端.地面解码接收端由于信道删除只接收到5个正确的测量值 (y3,y5,y6,y7,y8)和对应的序列号编码(3,1,2,3,0)组成的5维的测量值向量yH×1,yG×1中的y2在传输过程中出错,被地面解码接收端丢弃.地面解码接收端根据序列号编码(3,1,2,3,0)恢复出原始序列号(3,5,6,7,8).然后根据原始序列号从测量矩阵ΦM×N中找到与yH×1对应的Φ′H×N,利用重构算法正确重构出原始信号xN×1.
(1)井下编码发送端编码步骤如下:
步骤1:在一次编码前设置i=0,j=0;
步骤2:根据式(7)计算出yM×1;
步骤3:依次检查yM×1中元素yi,更新i=i+1,如果yi≤2n-1,表示yi没有发生溢出误差,保留yi的量化值和序列号编码i mod 4作为 的元素,更新j=j+1,如果yi>2n-1,表示yi发生溢出误差,丢弃yi;
步骤4:检查j的值.如果j<G,表示还需要精确测量值yi来构成yG×1,回到步骤3.如果j=G,编码结束,传送yG×1.
(2)地面解码接收端解码步骤如下:
步骤1:地面解码接收端从yG×1接收到的正确测量值组成向量yG×1;
步骤2:检查接收到的正确测量值个数.如果H<R,表示地面解码接收端没有接收到足够的测量值,无法重构出原始信号,解码结束.如果H≥R,进入步骤3;
步骤3:从yH×1的每个元素所带的序列号编码恢复出每个元素对应的原始序列号;
步骤4:根据原始序列号从测量矩阵ΦM×N中找到与yH×1对应的Φ′M×N;
步骤5:利用(8)式重构算法恢复xN×1,解码结束.
5 实验及性能分析
通过第3节的分析可知,测量值的溢出率和信道删除概率与地面解码接收端成功重构信号的概率直接相关,测量值的溢出率和信道删除概率越大则地面解码接收端重构信号失败的概率越大.因此为降低地面解码接收端重构信号失败的概率,只能从降低测量值的溢出率和信道删除概率入手.信道删除概率为信道固有特性在此不做讨论,本文仅从降低测量值溢出率方面入手提高随钻测量系统测井数据实时传输能力.
本文实验所采用数据为大庆石油管理局钻井工程技术研究院提供的大庆油田实际随钻测井实时数据.测井方法包括随钻电磁波电阻率测井、随钻双伽马射线测井、随钻地层密度测井和中子孔隙度测井等,实时测井数据传输手段采用钻井液压力正脉冲传输,测井数据记录格式为哈里伯顿公司测井综合系统EXCELL2000数据库格式[25].具体测井时间及井号如下:2008-11-12_TWT-A1 H,2008-6-30_NB35-2-A,2009-6-7_N209-P295,2009-6-9_TD206-P96,2009-6-18_X123-P80,2009-9-7_X5-3-P142.
5.1 溢出率减小方法性验证
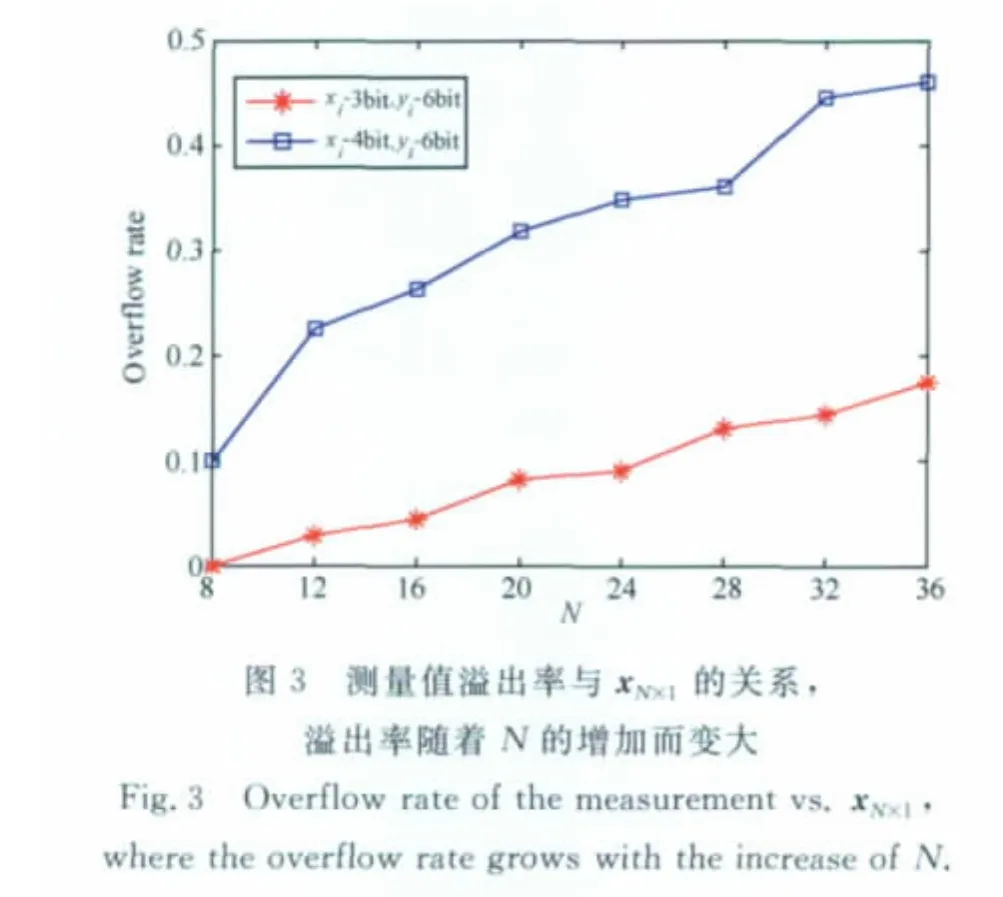
根据第二节的分析,通过信号预处理能以3比特或4比特表示原始测井数据xi,以6比特或7比特表示测量值yi.xi是式(7)中xN×1的元素,yi是式(7)中yM×1的元素.图3显示了测量值yi的溢出率与xN×1的关系,通过图3可以看出测量值yi的溢出率随着N的增加而变大.通过增加yi的比特数可以降低yi的溢出率,但是效率很低.因为增加比特数来降低溢出率的效果会随着N的增加越来越弱,而且增加比特数也会大大降低数据传输效率.因此必须用另外的方法来降低yi的溢出率.
分析式(7)可以看到影响yi的因素只有xN×1与测量矩阵ΦM×N.显然,xN×1中元素xi的值越小则yi的值也越小,yi的溢出率越低.第二节中已阐明,xN×1已经是通过信号预处理操作后的原始数据,数值已经比随钻传感器得出的原始数值减少很多.在确保不影响地面施工人员分析地层情况的前提下,xN×1的数值已没有进一步减少的空间.因此我们只能通过测量矩阵ΦM×N入手降低yi的溢出率.根据压缩感知理论,只要满足有限等距准则的矩阵就可以作为测量矩阵,因此有很大的自由空间来构造合适的测量矩阵ΦM×N降低yi的溢出率.本文通过构造改进的贝努利矩阵作为测量矩阵ΦM×N,大大降低了yi的溢出率.
贝努利矩阵是一种矩阵元素随机取值为+1或-1的矩阵,也就是说贝努利矩阵中行向量包含的+1或-1的个数是随机的.因此贝努利矩阵中某些行向量包含更多的+1而某些行向量包含更多的-1,某些行向量包含差不多数量的+1和-1.当与一个所有元素都为正整数的列向量xN×1相乘时,与前两种行向量相比,显然包含差不多数量+1和-1的行向量得到的乘积为一个较小数值的概率较大.也就是说假如测量矩阵ΦM×N都是由包含差不多数量+1和-1的行向量组成,式(7)中得到的yM×1的元素值都会偏小,即测量值yi的溢出率会降低.根据有限等距准则的性质,只要原始贝努利矩阵满足K阶有限等距准则,那么选择原始贝努利矩阵中包含差不多数量+1和-1的行向量组成的改进的贝努利矩阵也满足K阶有限等距准则,即本文所构造的改进的贝努利矩阵可以作为压缩感知框架中的测量矩阵ΦM×N.
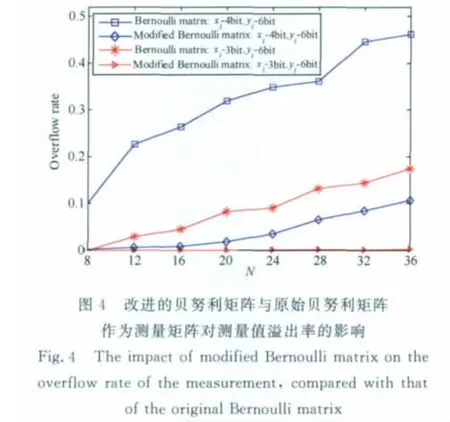
改进的贝努利矩阵构造方法如下.首先随机获得一个原始贝努利矩阵Φ2M×N或Φ3M×N,保证原始贝努利矩阵足够大能够从中选出改进的贝努利矩阵ΦM×N.然后选择原始贝努利矩阵中包含差不多数量+1和-1的行向量组成改进的贝努利矩阵ΦM×N作为测量矩阵.图4显示了使用改进的贝努利矩阵作为测量矩阵后测量值溢出率的下降情况.通过图4可以看出,使用改进的贝努利矩阵作为测量矩阵后测量值溢出率大大降低.
5.2 传输错误率降低方法有效性验证
根据式(4)的分析,当信道删除概率不变时井下发送测量值越多地面解码重构信号失败率越低.图5、图6和图7显示了当信道删除概率分别为0.02,0.06和0.10时地面解码端重构不同维数原始信号xN×1的失败概率与井下每次发送的测量值个数之间的关系.
从图5可看出,在地面施工人员选择12种测井数据实时传输(N=12)的情况下,当信道删除概率为0.02时,井下每次发送14个测量值即可将重构信号失败率降低到接近10-3,为此只需付出多发2个测量值的代价.当信道删除概率为0.06时井下每次发送16个测量值即可将重构信号失败率降低到接近10-3,为此需付出多发4个测量值的代价.而当信道删除概率为0.10时井下每次发送18个测量值可将重构信号失败率降低到接近10-3,为此需付出多发6个测量值的代价.

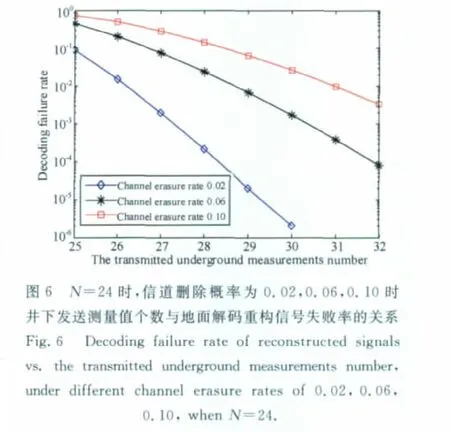
从图6可得出,在地面施工人员选择24种测井数据实时传输(N=24)的情况下,当信道删除概率为0.02时井下每次发送27个测量值即可将重构信号失败率降低到接近10-3,为此需付出多发3个测量值的代价.当信道删除概率为0.06时井下每次发送30个测量值即可将重构信号失败率降低到接近10-3,为此需付出多发6个测量值的代价.当信道删除概率为0.10时井下每次发送32个测量值可将重构信号失败率降低到接近10-3,为此需付出多发8个测量值的代价.
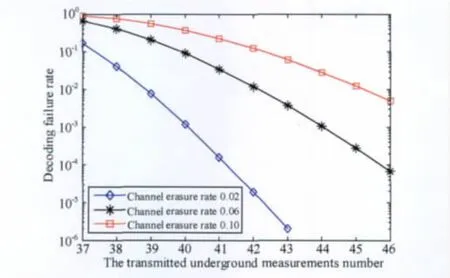
图7 N=36时,信道删除概率为0.02,0.06,0.10时井下发送测量值个数与地面解码重构信号失败率的关系Fig.7 Decoding failure rate of reconstructed signals vs.the transmitted underground measurements number,under different channel erasure rates of 0.02,0.06,0.10,when N=36.
从图7可看出,在地面施工人员选择36种测井数据实时传输(N=36)的情况下,当信道删除概率为0.02时井下每次发送40个测量值即可将重构信号失败率降低到接近10-3,为此需付出多发4个测量值的代价.当信道删除概率为0.06时井下每次发送44个测量值即可将重构信号失败率降低到接近10-3,为此需付出多发8个测量值的代价.当信道删除概率为0.10时井下每次发送46个测量值可将重构信号失败率降低到接近10-3,为此需付出多发10个测量值的代价.
5.3 数据传输实时性验证
通过图5、图6和图7的分析可以看出,信道删除概率越大,保证一次数据可靠传输所需发送的测量值也越多.换句话说,需要发送一定量的冗余数据来对抗信道删除特性,以提高传输可靠性.例如,若重构信号失败率为10-3,当信道删除概率为0.02时大约需要多发送10%的数据,当信道删除概率为0.06时大约需要多发送25%的数据,当信道删除概率为0.10时大约需要多发送40%的数据.而传统的方法不管道删除概率为多少,都需要多发送1倍的数据来提高可靠性.在这一节的实验中我们将验证本文方法利用发送少量冗余数据来换取数据可靠性后仍然还能很好地满足随钻测井的实时性要求.
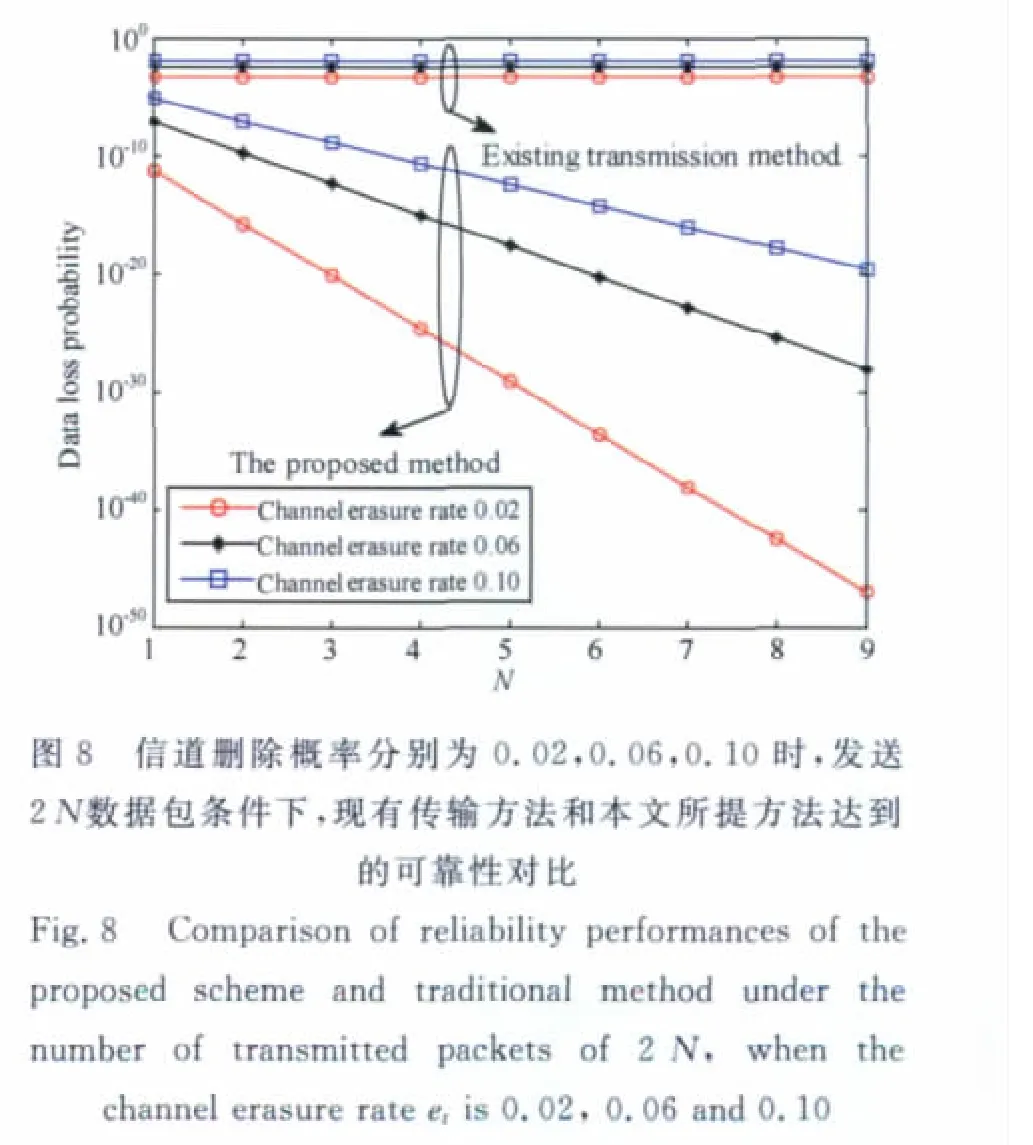
在工程实践中,随钻测井要求保证钻井轨迹上每1m至少1个数据测点.依据目前随钻测井钻进速率一般不超过35m/h计算可知随钻测井数据实时性指标约为2min,即要求井下随钻测井数据在2min内传输到地面系统.由于现有技术不能保证数据可靠传输.为确保钻井轨迹上每1m至少1个数据测点,传统方法采取在规定的2min时间内传送2次测井数据的做法,如此可将数据丢失概率从et降为.这样只要同一种测井数据在2次传输中成功传输一次就能达到数据实时性要求,即钻井轨迹上每1米至少1个数据测点.通过以上分析可以看出,只要CSCC传送一次测井数据的数据量不超过现有传输方法传输的数据量,即不超过原始测井数据数据量的2倍,就不会影响测井数据的实时性.从另一方面讲,在规定的2min内,采用CSCC只需传送一次数据就能达到比现有方法传送2次数据更高的传输可靠性.我们通过分析,比较了在不同信道删除概率条件下CSCC和现有传输方法的传输数据量和传输可靠性.从图8结果可以看出,在相同发送数据量的前提下,即发送数据量为2 N时,采用CSCC可以大大提高测井数据传输的可靠性.在et=0.02,0.06和0.10,分别可实现10-12,10-8,10-6量级以下的数据丢失率,这远远低于传统方法.图8结果同时也表明采用CSCC数据丢失率会随N取值的增大不断降低.
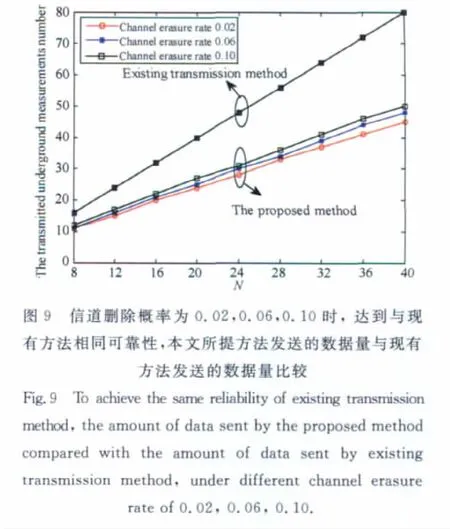
图9给出了在保持与现有方法同等的数据传输可靠性前提下,即数据丢失概率为e2t时,采用CSCC所需发送数据量的情况.可以看出,CSCC所需发送数据量要远远低于传统方法,因此采用CSCC在实现相同可靠传输时,可大大提高传输的实时性.在实际应用中,现场工人还可通过调整CSCC的发送数据量以满足施工现场不同信道删除概率和测井数据传输实时性可靠性要求,灵活性和适应性很强.
6 结 论
本文针对随钻测井中普遍使用的钻井液压力脉冲传输实时测井数据方式无法纠正传输过程中信道删除造成的测井数据错误问题,引入压缩感知理论到钻井液信道编码中,提出一种适用于钻井液信道数据可靠传输的压缩感知信道编码方法.理论分析和实验结果表明,本方法以较小的数据冗余大大降低了由于信道删除错误带来的测井数据错误率,在不影响测井数据传输实时性的前提下大大提高了测井数据传输的可靠性.测井人员能灵活调整本方法实现不同信道删除概率下的测井数据可靠传输.
本文的工作是在无任何反馈信息的假设下进行的,这属于最为保守的情况.在实际测井工作中,地面工作人员可以借助于改变钻井液压力等方法向井下设备传送简单的反馈信息.尽管这些反馈的信息量极其有限,但利用这些反馈信息会进一步提高系统的信息传输效率与性能.因此,本文的下一步研究工作将考虑在引入有限实时反馈情况下对所提基于压缩感知的随钻测井编码传输方法性能的改进和提升.
(References)
[1]苏义脑,窦修荣.随钻测量、随钻测井与录井工具.石油钻采工艺,2005,27(1):74-78.Su Y N,Dou X R.Measurement while drilling,logging while drilling and logging instrument.Oil Drilling &Production Technology (in Chinese),2005,27(1):74-78.
[2]李浩,刘双莲,魏修平.测井地质学在我国的发展历程及其启示.地球物理学进展,2010,25(5):1811-1819,doi:10.3969/j.issn.1004-2903.2010.05.039.Li H,Liu S L,Wei X P.Development history and enlightment of logging geology in China.Progress in Geophys.(in Chinese),2010,25(5):1811-1819,doi:10.3969/j.issn.1004-2903.2010.05.039.
[3]刘双莲,李浩,陆黄生.测井资料在储层预测研究中的应用.地球物理学进展,2010,25(6):2045-2053,doi:10.3969/j.issn.1004-2903.2010.06.021.Liu S L,Li H,Lu H S.The application of log data in the study of reservoir prediction.Progress in Geophys.(in Chinese),2010,25(6):2045-2053,doi:10.3969/j.issn.1004-2903.2010.06.021.
[4]陆斌,葛洪魁,吴何珍等.利用相关域小波变换进行SWD资料预处理.地球物理学报,2009,52(9):2349-2356.Lu B,Ge H K,Wu H Z,et al.SWD data preprocessing using wavelet transform of correlation domain.Chinese J.Geophys.(in Chinese),2009,52(9):2349-2356.
[5]吴何珍,葛洪魁,杨顶辉等.钻柱振动倒谱分析及其钻头源信号提取方法研究.地球物理学报,2010,53(8):1968-1975.Wu H Z,Ge H K,Yang D H,et al.A research of cepstrum analysis of drill string vibration and extracting the bit source signals.Chinese J.Geophys.(in Chinese),2010,53(8):1968-1975.
[6]李潮流,王环,柴细元.地层评价与测井技术新进展——第50届SPWLA测井年会综述.测井技术,2009,33(6):505-510.Li C L,Wang H,Chai X Y.Advances in formation evaluation and well logging technology——An overview of the SPWLA 50th annual logging symposium.Well Logging Technology (in Chinese),2009,33(6):505-510.
[7]刘新平,房军,金有海.随钻测井数据传输技术应用现状及展望.测井技术,2008,32(3):249-253.Liu X P,Fang J,Jin Y H.Application status and prospect of LWD data transmission technology.Well Logging Technology(in Chinese),2008,32(3):249-253.
[8]牛林林.随钻测井的数据传输.国外测井技术,2009,(6):7-9.Niu L L.Logging-While-Drilling data transmission.World Well Logging Technology (in Chinese),2009,(6):7-9.
[9]魏保君.一种新型随钻电阻率测井仪器的响应和刻度.地球物理学报,2007,50(2):632-641.Wei B J.Response and calibration of a new logging-while-drilling resistivity tool.Chinese J.Geophys.(in Chinese),2007,50(2):632-641.
[10]孙向阳,聂在平,赵延文等.用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应.地球物理学报,2008,51(5):1600-1607.Sun X Y,Nie Z P,Zhao Y W,et al.The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method.Chinese J.Geophys.(in Chinese),2008,51(5):1600-1607.
[11]张旭,魏宝君,刘坤等.利用积分方程的加速迭代算法计算随钻电磁波电阻率测量仪器的响应.地球物理学报,2009,52(9):2394-2401.Zhang X,Wei B J,Liu K,et al.Computing electromagnetic wave resistivity MWD tool′s response using accelerated iteration algorithm for integral equations.Chinese J.Geophys.(in Chinese),2009,52(9):2394-2401.
[12]张锋,袁超,王新光.脉冲中子双伽马谱饱和度测井方法及数值模拟研究.地球物理学报,2010,53(10):2527-2533,doi:10.3969/j.issn.0001-5733.2010.10.026.Zhang F,Yuan C,W ang X G.Study on the dual gamma spectrum saturation logging method based on pulsed neutron source and numerical simulation.Chinese J.Geophys.(in Chinese),2010,53(10):2527-2533,doi:10.3969/j.issn.0001-5733.2010.10.026.
[13]洪德成,杨善德.张量感应测井资料处理中若干问题的研究.地球物理学报,2009,52(4):1121-1130,doi:10.3969/j.issn.0001-5733.2009.04.030.Hong D C,Yang S D.A study on some problems of tensor induction well logging data processing.Chinese J.Geophys.(in Chinese),2009,52(4):1121-1130,doi:10.3969/j.issn.0001-5733.2009.04.030.
[14]李浩,刘双莲,魏修平.浅析我国测井解释技术面临的问题与对策.地球物理学进展,2010,25(6):2084-2090,doi:10.3969/j.issn.1004-2903.2010.06.026.Li H,Liu S L,Wei X P.Analysis of the problem and strategys in logging interpretation techniques in our country.Progress in Geophys. (in Chinese),2010,25(6):2084-2090,doi:10.3969/j.issn.1004-2903.2010.06.026.
[15]付建伟.重力测井技术若干进展.地球物理学进展,2010,25(2):596-601,doi:10,3969/j.issn.1004-2903.2010.02.032.Fu J W.Progress of gravity logging technology.Progress in Geophys.(in Chinese),2010,25(2):596-601,doi:10.3969/j.issn.1004-2903.2010.02.032.
[16]Donoho D L.Compressed Sensing.IEEE Trans.on Information Theory,2006,52(4):1289-1306.
[17]Tsaig Y,Donoho D L.Extensions of compressed sensing.Signal Processing,2006,86(3):533-548.
[18]Candes E.Compressive Sampling.∥ Proceedings of the International Congress of Mathematicians.Madrid,Spain,2006,3:1433-1452.
[19]Candes E,Romberg J. Quantitative robust uncertainty principles and optimally sparse decompositions.Foundation of Comput Math,2006,6(2):227-254.
[20]Candes E J,Romberg J, Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information.IEEE Trans.on Information Theory,2006,52(2):489-509.
[21]Candes E J,Tao T.Decoding by linear programming.IEEE Trans.on Information Theory,2005,51(12):4203-4215.
[22]Laska J N,Boufounos P T,Davenport M A,et al.Democracy in action:Quantization,saturation,and compressive sensing.Applied and Computational Harmonic Analysis,2011,31(3):429-443.
[23]张煜,裘正定,熊轲等.基于差分脉码调制的随钻测量数据压缩编码算法.石油勘探与开发,2010,37(6):748-755.Zhang Y,Qiu Z D,Xiong K,et al.An algorithm for MWD data compression based on differential pulse code modulation.Petroleum Exploration and Development (in Chinese),2010,37(6):748-755.
[24]Wei D,Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction.IEEE Transactions on Information Theory,2009,55(5):2230-2249.
[25]常文会,江明.EXCELL2000I测井系统.石油仪器,2008,22(3):21-24.Chang W H,Jiang M.EXECLL2000Iwell logging system.Petroleum Instruments(in Chinese),2008,22(3):21-24.

