价值转形：总量相等则个量相等

冯金华

一、引言

一个完整的和成功的价值转形理论需要同时解决两个关键问题：在利润平均化和价值转化为生产价格之后，一方面，每个部门生产的产品的生产价格通常不再等于相应的价值，平均利润通常不再等于相应的剩余价值，即 “个量”不一定相等；另一方面，整个经济的全部产品的生产价格之和仍然等于价值之和，平均利润之和仍然等于剩余价值之和，即“总量”仍然相等。

关于这两个问题，马克思曾有过多次明示。他说： “一般利润率，从而与各不同生产部门所使用的既定量资本相适应的平均利润一经形成，情况就不同了。现在，一个特殊生产部门实际生产的剩余价值或利润，同商品出售价格中包含的利润相一致，这只是一种偶然的现象。现在，不仅利润率和剩余价值率，而且利润和剩余价值，通常都是实际不同的量。”［1］（P187）但是， “一切不同生产部门的利润的总和，必然等于剩余价值的总和；社会总产品的生产价格的总和，必然等于它的价值的总和”。［2］（P193）

然而，在马克思之后 （甚至也包括马克思本人），所有的价值转形研究都没有能够同时回答这两个问题。实际上，迄今为止，绝大多数人忽略了“个量”问题，只是孤立地研究 “总量”问题，即试图解释在利润平均化和价值转化为生产价格之后，价值总量和生产价格总量以及剩余价值总量和平均利润总量是否可以保持一致。从方法上看，这些关于价值转形的讨论主要可以分为基于偏离系数方法的研究和基于技术系数方法的研究。20世纪60年代以前，研究者大多采取相对简单的偏离系数方法，即利用偏离系数来联系生产价格体系与价值体系，如Bortkiewicz［3］（P199－221）、Winternitz［4］（P276－280）、Meek［5］、Seton［6］（P149－160）等，但所得到的结论却都是否定的，即两个总量相等不能同时成立。60 年代以后，研究者大多采取复杂一些的技术系数方法，即通过技术系数来建立和求解生产价格体系和价值体系。其中，Samuelson［7］（P399－431）等人用技术系数来分别建立生产价格体系和价值体系，并得出两个总量相等不能同时成立的结论；Foley［8］（P37－47）和Dumenil［9］（P427－450）提出“劳动时间的货币表示 （MELT）”，用MELT 来联系两个体系，其结论是：如果讨论的是纯产品而非总产品，则两个总量相等可以同时成立；Kliman 和McGlone［10］（P33－59）提 出 “分期单一体系 （TSS）”，把生产价格和价值放在同一个体系中 （所谓 “单一体系”），且让本期的价值和生产价格取决于上一期的生产价格 （所谓“分期体系”），其结论是：在重新界定价值和剩余价值的概念后，可以同时有两个总量相等。

撇开传统价值转形研究一直未能真正说明两个总量相等这一点不论，其另外一个重要缺陷是没有注意到，在价值转形问题中， “总量”相等和 “个量”不等是相互矛盾的，二者不可能同时成立。换句话说，传统价值转型研究根本没有意识到：如果两个总量相等，则所有的个量 （即每种产品的生产价格和价值）亦必然会相等，反之，如果个量不等，则总量也不会相等。

笔者曾利用技术不变 （即不因价值到生产价格的转形而变化）、技术矩阵行列式不为零的假定和再生产的条件证明，在马克思的价值—生产价格体系中，如果整个社会的生产价格总量等于价值总量且平均利润总量等于剩余价值总量，则每一种产品的生产价格就必然等于相应的价值。［11］这个结论不仅在简单再生产的条件下成立，而且在扩大再生产的条件下也成立。

尽管从马克思主义经济学特别是从马克思再生产理论的角度来看，在价值转形的研究中引入再生产的条件是十分自然和非常合理的［12］，但仍然有人对此提出了不同的意见。例如，丁堡骏［13］和裴宏［14］认为，在讨论价值转形问题时，不应当考虑再生产的条件或价值的实现。这种看法是错误的。理由很简单：如果价值从而剩余价值不能得到实现，则平均利润率 （它在马克思那里等于剩余价值总量与预付资本总量的比率）的概念就失去了意义，从而，以平均利润率为基础的价值转形问题也就失去了意义。

实际上，通过进一步的研究可以发现，在讨论价值转形问题时，即使不去考虑再生产的条件，得到的结论也是一样的，即若总量相等，则个量亦必然相等。此外，上述关于技术矩阵行列式不为零的假定也不够 “基本”，可以从其他一些更加宽松也更加简单的假定推导出来。换句话说，我们可以根据一些更加基本和更加合理的假定，且完全用不着依靠简单再生产或扩大再生产的条件，来证明 “总量相等则个量亦相等”的结论。

本文的基本思路是：首先，根据马克思关于两大部类社会总产品构成的理论构造其价值体系和相应的生产价格体系，并对价值体系和生产价格体系中的经济变量和消耗系数做出合理的假定；其次，利用两个总量相等的假定建立价值体系和生产价格体系之间的联系，使得对价值与生产价格之间关系的分析成为可能；最后，逐一分析由价值体系、生产价格体系和两个总量相等条件构成的价值转形模型的各种可能的情况，并证明在所有这些情况下，每一部类的商品的生产价格都恰好等于相应的价值。

二、模型和假定

马克思关于社会总产品的构成包括实物和价值两个方面：从实物方面看，社会总产品可分为两大部类，即生产生产资料的第一部类和生产消费资料的第二部类；从价值方面看，社会总产品可分为三个部分，即不变资本、可变资本和剩余价值。因此，若用 “1”和 “2”分别表示第一部类和第二部类，用c、v和m分别表示以价值来计量的不变资本、可变资本和剩余价值，用w表示产品价值总量，则有：

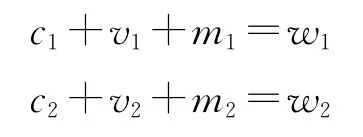
上述社会总产品的两大部类价值构成模型可以进一步具体化。首先，把每一部类的产品价值总量wi（i＝1，2）看成相应的单位产品价值 （用zi表示）和产量 （用qi表示）的乘积，即wi＝ziqi。其次，每一部类的生产都同时需要不变资本和可变资本，或者说，同时需要两大部类的产品作为投入，特别是，在价值上等于可变资本的消费资料部分被用于劳动力的生产，劳动力又被用于产品的生产。因此，若假定第一部类每生产一单位生产资料所消耗的第一和第二部类的产品量分别为a11和a12，它生产q1的生产资料所消耗的第一和第二部类的产品量就分别为a11q1和a12q1，相应的价值消耗量则分别为z1a11q1（＝c1）和z2a12q1（＝v1）；另一方面，若假定第二部类每生产一单位消费资料所消耗的第一和第二部类的产品量分别为a21和a22，它生产q2的消费资料所消耗的第一和第二部类的产品量就分别为a21q2和a22q2，相应的价值消耗量则分别为z1a21q2（＝c2）和z2a22q2（＝v2）。①为简单起见，这里假定，在每一次生产过程中，所有的不变资本和可变资本一样，均被完全消耗掉。于是得到如下明确反映技术关系的价值体系：

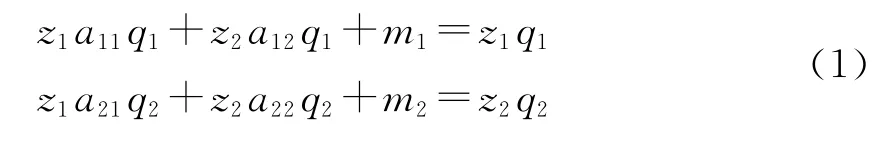
社会总产品的构成不仅可以用价值来表示，而且也可以用生产价格来表示。实际上，在利润平均化之后，它应当和必须用生产价格来表示。在马克思那里， “商品的生产价格，等于商品的成本价格加上依照一般利润率按百分比计算应加到这个成本价格上的利润，或者说，等于商品的成本价格加上平均利润”。［15］（P177）因此，若假定整个社会的平均利润率为r，则社会总产品的两大部类生产价格构成就可表示为：

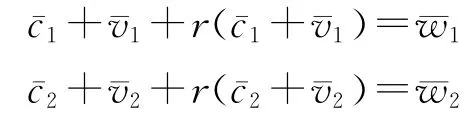
同样，每一部类产品的生产价格总量（i＝1，2）也可以进一步看成为单位生产价格（用pi表示）和产量的乘积，即＝piqi。由于单纯地从价值到生产价格的转化并不会影响经济的消耗系数，故现在第一部类每生产一单位生产资料所消耗的第一和第二部类的产品数量仍然为a11和a12，从而，它生产q1的生产资料所消耗的第一和第二部类的产品数量仍然为a11q1和a12q1，但相应的生产价格消耗量则为p1a11q1（＝）和p2a12q1（＝）；第二部类每生产一单位消费资料所消耗的第一和第二部类的产品数量仍然为a21和a22，从而，它生产q2的消费资料所消耗的第一和第二部类的产品数量仍然为a21q2和a22q2，但相应的生产价格消耗量则为p1a21q2（＝c2）和p2a22q2（＝）。于是又得到如下明确包括技术关系在内的方程组：

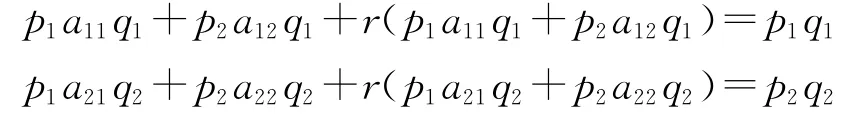
若令两大部类的平均利润分别为：

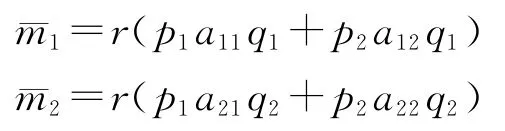
则有：

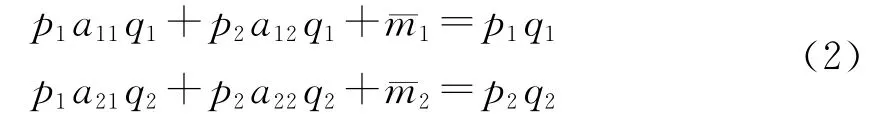
方程组 （2）是相应于价值体系 （1）的生产价格体系。换句话说，通过在价值体系 （1）中用生产价格代替相应的价值以及用平均利润代替相应的剩余价值，即可得到所谓的生产价格体系。有人认为价值体系 （1）和生产价格体系（2）是 “同一个内容”［16］，这是一种错觉。实际上，只有在假定 “两个总量相等”，从而 （如后面将要证明的）每一种商品的生产价格都等于相应的价值的条件下，它们才是相同的。

为了保证价值体系 （1）和生产价格体系（2）在经济上有意义，我们假定所有的经济变量（包括产量q1和q2、价值z1和z2、生产价格p1和p2、剩余价值m1和m2、平均利润m1和m2以及平均利润率r）和消耗系数 （即a11、a12、a21、a22）都大于零。假定所有的经济变量都大于零的合理性是显而易见的。例如，如果某一部类的产出（或价值、生产价格）为零，则这一部类就将不再存在；如果某一部类的剩余价值 （或平均利润）为零，则这一部类的生产就不是马克思所说的典型的资本主义生产。特别是，剩余价值和平均利润大于零意味着，整个经济生产的总产品在补偿原来的生产消耗之后还有剩余。这些剩余可被用于积累（包括追加的生产资料和追加工人的消费资料）或资本所有者的个人消费。实际上，如果不考虑经济上的合理性，仅从抽象的数学意义上讲，关于变量的假定还可以进一步放松。例如，两大部类的剩余价值中只要有一个大于零即可，另外一个则既可以大于零，也可以等于零。

另一方面，假定所有的消耗系数都大于零则保证了前面所说的，无论是生产资料的生产还是消费资料的生产，都同时需要不变资本和可变资本。同样，如果不考虑经济的含义，只从纯粹数学的角度来看，关于消耗系数的假定也可以进一步放松，即放松到只需要 “交叉”消耗系数a12和a21大于零，“自身”消耗系数a11和a22则既可以大于零，也可以等于零。在更加一般的包括n（n＞2）个部门的经济中，甚至可以允许某些交叉消耗系数等于零。

根据上述假定即所有的经济变量和消耗系数均大于零可以证明［17］，由消耗系数构成的如下行列式 （为方便起见，称为价值体系和生产价格体系的技术矩阵行列式，简称为技术矩阵行列式）不等于零，即：

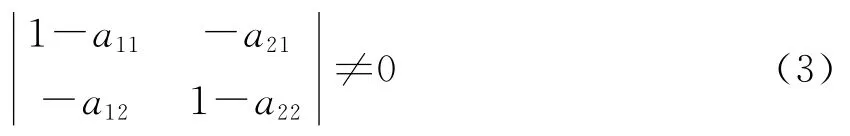
例如，由假定m1＞0、a12＞0和m2＞0、a21＞0，可从价值体系 （1）的第一式和第二式分别得到z1a11＋z2a12＜z1和z1a21＋z2a22＜z2，或 者z2a12／（1－a11）＜z1和z1＜z2（1－a22）／a21。①这里，由经济变量和消耗系数大于零的假定亦可知1－a11＞0 （以及1－a22＞0），从而a11＜1 （以及a22＜1），即所有的自身消耗系数均小于1。最后的两个不等式合在一起意味着z2a12／（1－a11）＜z2（1－a22）／a21，亦即a12／（1－a11）＜（1－a22）／a21，或者1－a11－a22－a12a21＋a11a22＞0。上式不等号的左边显而易见就等于 （3）式中的技术矩阵行列式。②在两大部类的剩余价值m1 和m2 中，即使有一个等于零，但只要另外一个大于零，就仍然可以推导出技术矩阵行列式不等于零的结果。

实际上，技术矩阵行列式不等于零即 （3）式是价值体系 （1）有唯一解的充分必要条件。为说明这一点，我们用q1和q2分别除以 （1）的两个方程可以得到：

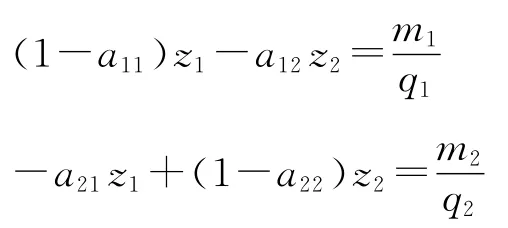
容易看到，这个方程组的系数行列式 （的转置）就是（3）式中所说的技术矩阵行列式。因此，如果它等于零，则方程组要么无解，要么有无穷多组解。前者意味着价值体系 （1）是矛盾的，因为满足它的价值根本就不存在，后者意味着价值体系 （1）是不确定的，因为满足它的价值有无穷多组。无论哪种情况，都不符合马克思劳动价值论的基本原理——商品的价值量由生产商品的社会必要劳动时间决定。需要说明的是，在不等式 （3）成立的条件下，尽管价值体系（1）的解是唯一的，但生产价格体系 （2）的解却不是唯一的，因为平均利润m1和m2是由模型中的其他因素决定的。

最后，假定“两个总量相等”，即在利润平均化和价值转化为生产价格之后，整个社会的生产价格总量等于价值总量、平均利润总量等于剩余价值总量。该假定在两大部类经济中可以表示为：

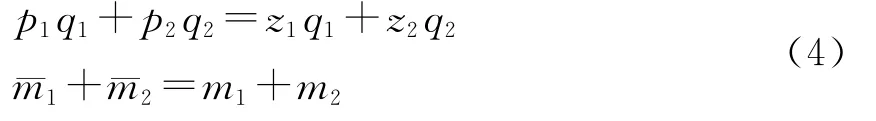
现在要讨论的问题是：在给定价值体系（1）、生产价格体系 （2）以及假定所有的经济变量和消耗系数均大于零从而技术矩阵行列式不等于零即 （3）式成立的条件下，如果两个总量相等，即 （4）式成立，每一种商品的生产价格与相应的价值会具有什么样的关系？

三、总量相等和个量相等

初看起来，分析上述模型似乎很难得到肯定的判断，因为它含有10个变量（即两个产量q1和q2、两个价值z1和z2、两个生产价格p1和p2、两个剩余价值m1和m2、两个平均利润m1和），但却只有6个方程，包括价值体系 （1）的两个方程、生产价格体系（2）的两个方程以及两个总量相等条件（4）中的两个方程。

许多研究价值转形的学者都特别关注转形模型中方程数目与变量数目是否相等的问题。［18］然而，我们的研究却表明，这是一种肤浅的认识。他们没有注意到模型本身的特殊结构，以及由这种特殊结构所可能带来的特殊结果。实际上，根据价值体系 （1）和生产价格体系 （2），完全可以得到一个非常明确的同时也是非常简单的结论，即在假定所有的经济变量和消耗系数均大于零从而技术矩阵行列式不等于零即公式 （3）成立的条件下，如果两个总量相等，即公式 （4）成立，则每一种商品的生产价格都将毫无例外地等于它们的价值，即所有的个量必然相等。

证明上述结论的关键是根据 “两个总量相等”的条件之一即平均利润总量等于剩余价值总量或 （4）中的第二式来建立马克思的价值体系和相应生产价格体系之间的联系。［19］通过这一联系，可以非常清楚地看到生产价格与价值的关系。具体步骤如下：

首先，将价值体系 （1）的两个公式相加和整理得到：

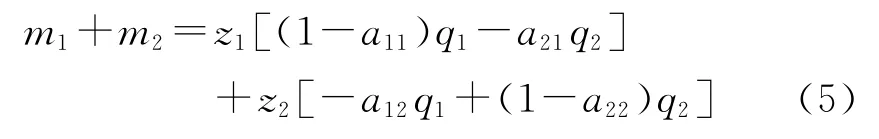
其次，将生产价格体系 （2）的两个公式同样相加和整理得到：

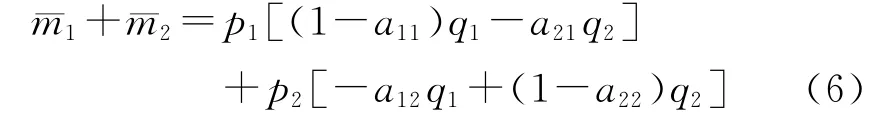
最后，根据平均利润总量等于剩余价值总量的假定，把（5）式和 （6）式综合为：

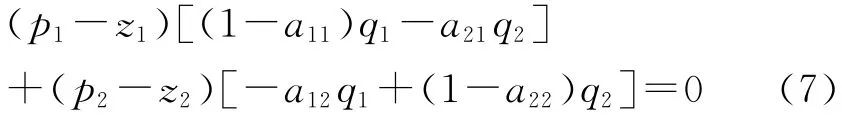
现在可以看到，通过平均利润总量等于剩余价值总量的假定，价值体系 （1）和生产价格体系 （2）被联系在一起，从而使得对价值与生产价格之间关系的分析成为可能。这就是 （7）式的重要意义所在。下面要利用这个公式来证明所有商品的生产价格与价值均相等。

不难看出，在（7）式中，（1－a11）q1－a21q2＝q1－（a11q1＋a21q2）是生产资料的 “增量”，或“剩余”的生产资料，即生产资料的产出与投入之差。其中，q1是第一部类生产的生产资料，a11q1＋a21q2是两大部类用于投入的生产资料。－a12q1＋（1－a22）q2＝q2－（a12q1＋a22q2）是消费资料的 “增量”，或 “剩余”的消费资料，即消费资料的产出与投入之差。①这里需要注意的是，剩余生产资料的价值并不等于第一部类的剩余价值，剩余消费资料的价值也不等于第二部类的剩余价值。它们是两类完全不同的概念。其中，q2是第二部类生产的消费资料，a12q1＋a22q2是两大部类用于投入的消费资料。②如前所述，所谓 “用于投入的消费资料”实际上是指用于劳动力再生产的消费资料。

剩余生产资料和剩余消费资料总共有四种不同的组合：二者都等于零；前者不等于零而后者等于零；前者等于零而后者不等于零；二者都不等于零。在所有这些情况下，根据生产价格总量等于价值总量的假定以及技术矩阵行列式不等于零的推论，p1－z1和p2－z2都必然等于零，从而必然有p1＝z1、p2＝z2。对于上述四种组合分别讨论如下：

1.剩余生产资料和剩余消费资料都等于零

该组合用公式表示即为如下的方程组：

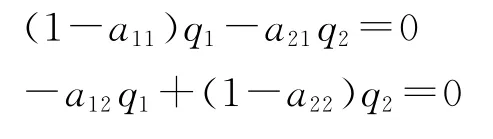
在这种情况下，根据系数行列式不等于零可知，上述方程组只有零解，即两大部类的产出都等于零。这显然是没有意义的。为了避免出现这种没有意义的结果，必须假定每一部类的剩余价值均为零——当每一部类的剩余价值均为零时，即使剩余生产资料和剩余消费资料都等于零，两大部类的产出仍然可以都为正数。于是，在这种情况下，剩余生产资料和剩余消费资料都等于零代表的就是一种产品生产的简单循环：所有产品的数量在生产过程的开始和结束时完全相同。③这就是亚当·斯密所说的 “伊甸园经济”。

在这种简单的、剩余产品和剩余价值均为零的产品生产循环中，价值体系可以简化为：

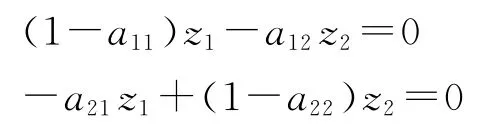
但是，一旦假定每一部类的剩余价值都等于零，则相应的平均利润率就等于零，从而，每一部类的平均利润也等于零。于是，相应的生产价格体系也简化为：

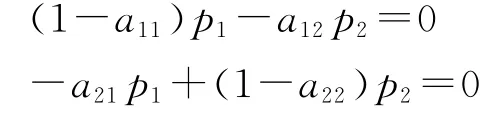
容易看到，简化的价值体系与生产价格体系在结构上是完全一样的，除了代表价值和生产价格的符号不同之外。如果它们的系数行列式不等于零，则有z1＝0、z2＝0 以及p1＝0、p2＝0，即生产资料和消费资料的价值和生产价格都等于零，这对我们的分析来说是没有意义的；如果它们的系数行列式等于零①注意，在假定两大部类的剩余价值均等于零时，技术矩阵行列式有可能等于零。，则其中就有一个方程是多余的。略去多余的方程 （如略去第二个方程）后即可得到：

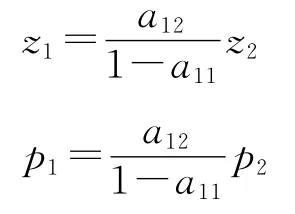
将上述结果代入生产价格总量等于价值总量的条件即可得到p1＝z1、p2＝z2。这意味着，当剩余生产资料和剩余消费资料均为零 （以及剩余价值亦均为零）时，所有商品的生产价格都恰好等于其价值。

2.剩余生产资料不等于零、剩余消费资料等于零

例如，设剩余生产资料为b1＞0。②此时，b1 不能小于零，否则，产量就会为负。于是有：

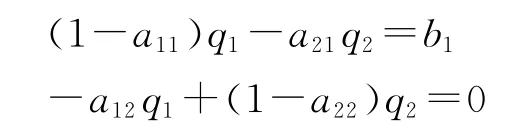
与第一种情况即剩余生产资料和剩余消费资料均为零相同，在上式中，由于系数行列式不等于零，故它的解也是唯一的。所不同的是，由于现在是剩余生产资料大于零，这个唯一的解不再是零解，而是正解，即两大部类的产量均大于零。此外，由于两大部类的产量均大于零，故整个经济的剩余价值总量和平均利润总量都可以大于零，从而，每一部类的剩余价值和平均利润亦可以大于零。

将该方程组中的两个方程代入 （7）式后得到：

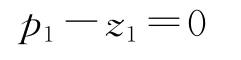
即p1＝z1。再将p1＝z1代入生产价格总量等于价值总量的条件，得到：

本文参考物联网体系架构，在感知层、传输层和应用层三层架构的基础上，针对智能楼宇的行业应用需求及特点，引入接入层和平台层的概念，形成了智能楼宇综合管理系统的五层架构参考模型。通过接入层设备的统一接入解析和平台层数据的统一存储处理，为智能楼宇各信息化系统的互联互通和融合管理提供了一种创新性的解决方案思路。

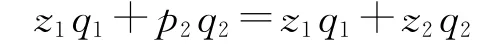
从而有p2＝z2。

3.剩余生产资料等于零、剩余消费资料不等于零

例如，设剩余消费资料为b2＞0。③同样，为保证产量不为负，这里的b2 也不能小于零。于是有：

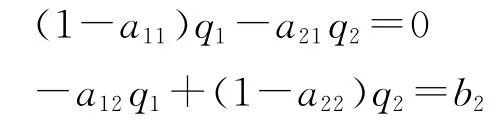
与第二种情况类似，此时，方程组也有唯一的正解，即两大部类的产量均大于零，从而，它们的剩余价值和平均利润亦可以都大于零。

将该方程组的两个方程代入 （7）式后得到：

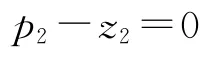
即p2＝z2。再将p2＝z2代入生产价格总量等于价值总量的条件，得到p1＝z1。

4.剩余生产资料和剩余消费资料都不等于零

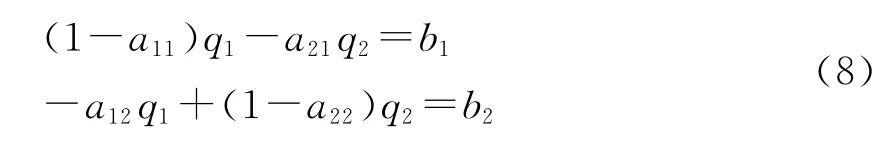
在这种情况下，首先可以证明［20］，在 （7）式中，p1－z1和p2－z2至少有一个要等于零，因为如果不是这样，即它们都不等于零，则用不等于零的p1－z1和p2－z2分别去乘 （8）式的第一式和第二式，并将所得到的第一式加到第二式上，就可得到：

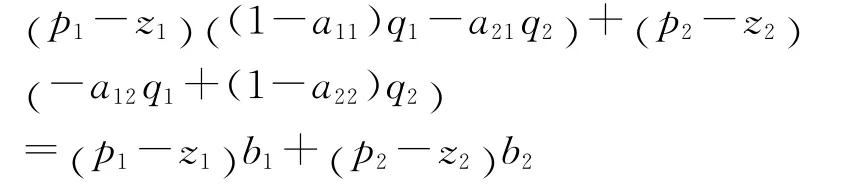
由于任意给定b1和b2，由 （8）式可解得确定的q1和q2，但由 （7）式，无论b1和b2从而q1和q2为何值，在上式中，左边总是等于零，而右边却并非也是如此。例如，当选取不同的（b1，b2）组合时，上式右边不可能都等于零。这与原方程组 （8）有唯一解的结果相矛盾。于是，p1－z1和p2－z2至少有一个要等于零。

其次，容易看到，在 （7）式中，如果p1－z1和p2－z2有一个等于零，则另外一个也必然等于零。例如，设p2－z2＝0。于是， （7）式简化为：

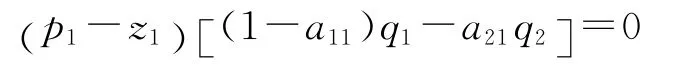
而由于 （1－a11）q1－a21q2≠0，故上式意味着p1－z1＝0。

由此可见，当剩余生产资料和剩余消费资料均不等于零时，必然有p1－z1＝0和p2－z2＝0，从而有p1＝z1和p2＝z2。

以上讨论还可以换一种方式进行。例如，由生产价格总量等于价值总量的条件可得：

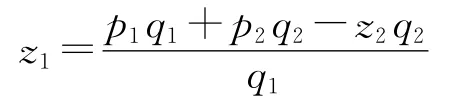
再将上式代入 （7）式后有：

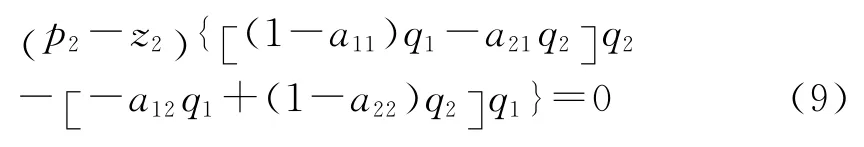
由于在上面的推导过程中，价值体系、生产价格体系以及两个总量相等的条件对任意允许的产出都成立，故所得到的结果即公式 （9）也对任意允许的产出q1和q2都成立。换句话说，公式 （9）实际上是一个 “恒等式”，即无论产出取何值，等式的左边总是等于零。这意味着p2－z2＝0。例如，由于公式 （9）对任意允许的产出都成立，我们可以这样来选择q1和q2，使得：

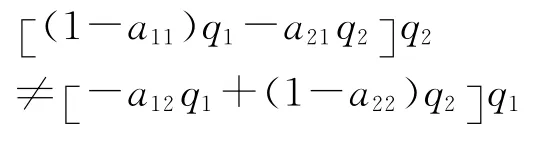
于是有p2－z2＝0，从而必有p2＝z2以及p1＝z1。

为了更加深入地了解在两个总量相等条件下生产价格必然等于价值的经济原因，我们可由上述不等式进一步解得：

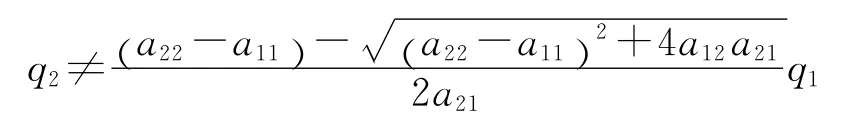
和

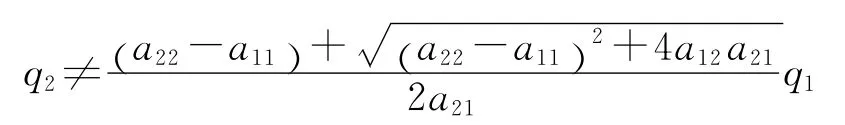
由于第一个不等式总是成立，故关键是看第二个不等式。

另一方面，通过求解生产价格体系可知，在两大部类的生产价格之间，存在着如下的关系［17］：

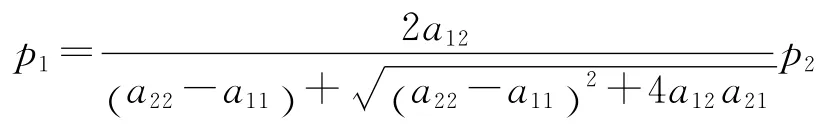
将上式与前面关于q1和q2的不等式综合起来即可得到：

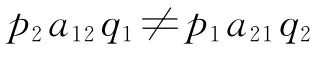
其中，左边的p2a12q1是以生产价格表示的第一部类的可变资本，即v1，右边的p1a21q2是以生产价格表示的第二部类的不变资本，即c2，故上式意味着，以生产价格表示的第一部类的可变资本不能等于第二部类的不变资本，即

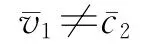
由此可见，在马克思的价值—生产价格体系中，如果以生产价格计量的第一部类的可变资本不等于第二部类的不变资本，则每一部类产品的生产价格就必然等于相应的价值。

那么，在什么样的情况下，以生产价格计量的第一部类的可变资本会不等于第二部类的不变资本呢？

抽象地说，似乎没有什么理由可以断言，在生产价格体系中，第一部类的可变资本和第二部类的不变资本一定相等或一定不等。我们至多只能认为，不等的可能性要远远大于相等的可能性。但是，一旦我们考虑实际的再生产过程，则结论就会变得十分明确：在生产价格体系中，第一部类的可变资本一定不等于第二部类的不变资本，从而，所有产品的生产价格一定等于相应的价值。

首先容易看到，在简单再生产的情况下，以生产价格计量的第一部类的可变资本一定不等于第二部类的不变资本。这是因为，生产价格体系的简单再生产要求，以生产价格计量的第一部类的可变资本加平均利润必须等于第二部类的不变资本，即

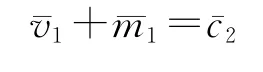
由于根据假定，平均利润不等于零，即m1≠0，故上式意味着v1≠c2。这就证明，在简单再生产的条件下，当以生产价格计量的第一部类的可变资本加平均利润等于第二部类的不变资本时，每一部类产品的生产价格必然等于它们的价值。

其次，来看扩大再生产。生产价格体系的扩大再生产条件是：以生产价格计量的第一部类的原有可变资本、追加可变资本、资本所有者的个人消费三者之和等于第二部类的原有不变资本加上追加不变资本。用公式表示为：

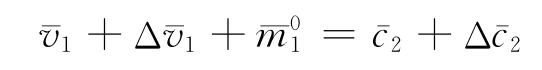
这里，v1、Δv1和m01代表以生产价格计量的第一部类的可变资本、追加可变资本和资本所有者的个人消费，c2和Δc2代表以生产价格计量的第二部类的原有不变资本和追加不变资本。

与简单再生产不同，抽象地看，从扩大再生产的条件本身并不能确定第一部类的 （原有）可变资本和第二部类的 （原有）不变资本是相等还是不等。换句话说，在生产价格体系的扩大再生产情况下，第一部类的 （原有）可变资本v1与第二部类的 （原有）不变资本c2既可能不等，也可能相等。如果不等，则自然就得到与前面相同的结论，即所有产品的生产价格都等于相应的价值；如果相等，则我们就暂时还不能够说，每种产品的生产价格仍然等于其价值。尽管不相等是通常的情况，而相等是非常特殊的，但也不能简单地否定其存在的可能性。

但是，如果我们把再生产看成是一个连续的过程 （假定至少持续两个时期），则可以发现，第一部类的可变资本恰好等于第二部类不变资本的情况不仅是 “非常偶然”的，而且也是 “极其短暂”的，很快就会消失。换句话说，即使一开始时 （例如在第一期），第二部类的不变资本恰好等于第一部类的可变资本，从而，在该时期中，生产价格可能不会等于相应的价值，但在接下来的第二期 （以及以后各个时期）中，第一部类的可变资本就将不会再等于第二部类的不变资本。这是因为，在第一期的扩大再生产结束之后，第一部类的可变资本从v1增加到v1＋Δv1（注意，不是增加到v1＋Δv1＋m01，因为其中的m01部分是被资本所有者消费掉的，并没有形成可变资本），第二部类的不变资本从原来的c2增加到c2＋Δc2，由于v1＋Δv1＜c2＋Δc2，故在第二期中，第一部类的可变资本和第二部类的不变资本就将不再相等，而且，从第二期开始，以后永远也不会再相等。换句话说，即使在开始时，第一部类的可变资本和第二部类的不变资本因为某种巧合 （尽管这种巧合实际上很少发生）而相等，但在再生产的过程中，也会变得不再相等。因此，考虑到再生产过程的持续性，即使一开始时生产价格可能会偶然地不等于价值，但立刻就会变得重新相等起来。

由此可见，在生产价格体系的简单再生产条件下，即当第一部类的可变资本加平均利润等于第二部类的不变资本时，所有产品的生产价格都等于相应的价值；在生产价格体系的扩大再生产条件下，即当第一部类的原有可变资本加追加可变资本再加资本所有者的个人消费恰好等于第二部类的原有不变资本加追加不变资本时，除了极个别的情况，所有产品的生产价格也总是等于相应的价值，而在例外的情况下，尽管生产价格和价值一开始时可能不相等，但经过短暂 （即一个再生产时期）的调整之后，仍然会归于相等。

综上所述，在本文所给的相当宽松和十分自然的假定条件下，如果两个总量相等，即在利润平均化之后，社会总产品的生产价格总量等于价值总量且平均利润总量等于剩余价值总量，则所有的个量也相等，即每一种商品的生产价格都等于相应的价值。尽管在上述推导过程中，每一步都非常简单和平淡无奇，但所得到的结论却相当地出人意料。特别提醒注意的是，这个结论不会因为价值、剩余价值、平均利润等变量以及消耗系数取值的不同而改变。换句话说，无论这些变量和系数如何变化，只要均大于零，生产价格就一定等于相应的价值。

上面的讨论还可以更具体地从再生产的角度来进行 （尽管这不是必需的）。例如，我们把每一部类的剩余价值都分解为三个部分，即新增加的不变资本、新增加的可变资本和资本所有者的个人消费，从而，把价值体系 （1）（生产价格体系（2）也一样）表示为：

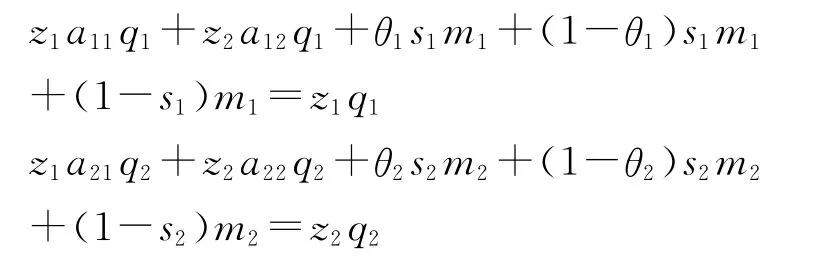
这里，si∈［0，1］代表第i部类的剩余价值中用于积累的比率，θi∈［0，1］代表积累中用于不变资本的比率，从而，θisimi、（1－θi）simi和（1－si）mi分别是新增的不变资本、可变资本和资本所有者的个人消费。

为了保证再生产顺利进行，第一部类的原有可变资本、新增可变资本与资本所有者的个人消费之和必须等于第二部类的原有不变资本与新增不变资本之和，即：

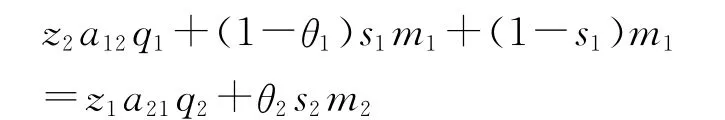
按照上述条件进行两大部类之间的产品交换之后，价值体系变为：

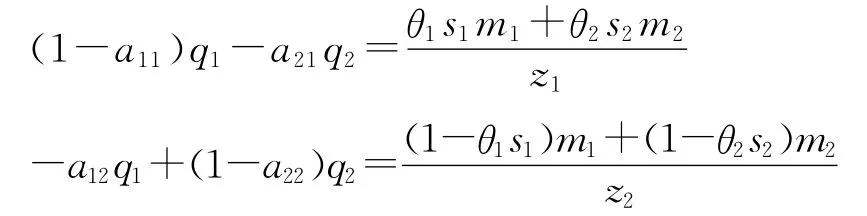
在上面两式中，如果右边均不为零，则得到的就是前面讨论过的第四种情况，即剩余生产资料和剩余消费资料均不为零。这种情况可以看成是最一般形式的扩大再生产。此时，至少有一个部类的剩余价值不为零 （如m1≠0）且剩余价值中至少各有一部分被用于新增不变资本和可变资本 （如s1≠0、θ1≠0）。

如果mi＝0，即两大部类的剩余价值均为零，则得到：

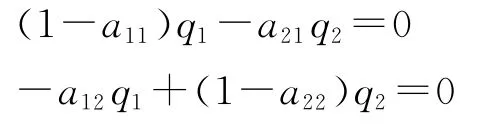
这就是前面讨论过的第一种情况，即剩余生产资料和剩余消费资料均为零。

如果mi≠0，但si＝1且θi＝1 （即两大部类的剩余价值均用于积累且只用于新增的不变资本，而不用于新增的可变资本），则得到：

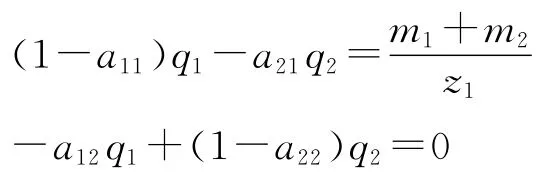
这就是前面讨论过的第二种情况，即剩余生产资料不为零，但剩余消费资料为零。

如果mi≠0但si＝0 （即两大部类的剩余价值均不用于积累①这就是通常所说的 “简单”再生产。），或者si≠0 但θi＝0 （即两大部类的积累均只用于新增的可变资本，而不用于新增的不变资本②这种 “扩大”再生产的条件与简单再生产是完全相同的，即最终都可归结为第一部类的可变资本加剩余价值等于第二部类的不变资本。这里顺便纠正一个可能会有的误解，即把 “第一部类的可变资本加剩余价值等于第二部类的不变资本”只看成是简单再生产的条件。实际上，如我们上面所看到的，它也是一种特殊形式的扩大再生产 （即只有可变资本积累的扩大再生产）的条件。），则得到：

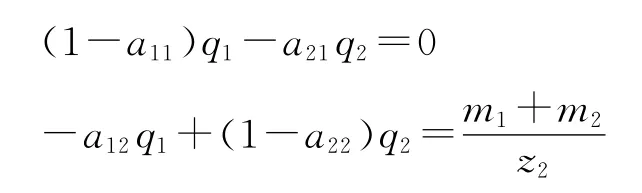
这就是前面讨论过的第三种情况，即剩余生产资料为零，但剩余消费资料不为零。

此外，还可以讨论其他一些特殊情况，如只有某一部类的剩余价值用于积累，另一部类的剩余价值不用于积累，或者，某一部类的积累只用于新增的不变资本，另一部类的积累只用于新增的可变资本等。不过，所有这些都可以看成是第四种情况或者一般形式的扩大再生产的特例，不会给我们的分析带来任何新的不同的结果。

因此，从再生产的角度来看，我们前面的讨论实际上又表明：无论再生产的性质如何，无论它是简单的还是扩大的，或者其他类型的 （如两大部类的积累均用于新增不变资本或新增可变资本），只要两个总量相等，则所有的个量亦必然相等。

四、结论

以上讨论可以概括如下：在假定价值体系和生产价格体系中的经济变量和消耗系数均大于零（从而技术矩阵行列式不等于零）的条件下，只要平均利润总量等于剩余价值总量且生产价格总量等于价值总量，则每一种商品的生产价格就等于相应的价值。

从再生产的角度来看，上述结果 （尽管这些结果实际上与再生产的性质并没有必然的联系）还可以表示为：在所有的再生产情况下，如果平均利润总量等于剩余价值总量且生产价格总量等于价值总量，则每一种商品的生产价格就等于相应的价值。

总之，在假定经济变量和消耗系数均大于零的条件下，如果整个经济的平均利润总量等于剩余价值总量且生产价格总量等于价值总量，则每一部类的单位商品的生产价格就等于其价值；反之，如果每一部类的单位商品的生产价格不等于其价值，则整个经济的生产价格总量也不会等于其价值总量。简言之，如果“总量”相等，则“个量”就一定相等；反之，如果“个量”不等，则“总量”也不会相等。这个结果与再生产的性质（如简单再生产、扩大再生产，或其他类型的再生产）没有必然的联系，与模型中经济变量和消耗系数的取值也没有任何关系，只要它们均大于零即可。①尽管本文分析的是两部类经济，但由讨论的过程可以看到，在更多个部门的经济中，亦可以得到同样的结论。

由此，我们可以在非常一般的条件下引申出如下几点结论：②这些结论也曾在一些比较特殊的条件下得到过。参见冯金华：《价值转形：一个伪问题》，载 《经济评论》，2008 （3）；《不必要的生产价格——再论价值转形是一个伪问题》，载 《经济评论》，2009 （4）；《生产价格会偏离价值吗？——三论价值转形是伪问题、兼评几种偏离系数转形模型》，载 《经济评论》，2010 （3）。第一，价值转形问题是一个伪问题。因为在两个总量相等的条件下，所谓的价值转形，只是每一部门的产品的价值转化为在数量上与自己完全相等的生产价格。从这个意义上说，价值到生产价格的转形不过是一种 “假转形”，或者不如说，价值转形问题实际上是一个“伪问题”。第二，生产价格概念是一个不必要的概念。由于在利润平均化之后，价值并没有真的转化为某个与自己在量上不等的东西，故我们也可以说，生产价格是一个不必要的概念。第三，劳动价值论是一个彻底的科学理论。说生产价格是一个不必要的概念，并不意味着马克思的劳动价值论遭到了颠覆，恰恰相反，这更加显示出劳动价值论是一个非常彻底的理论：由于在利润平均化之后，价值仍然保持着自身的数量不变，而非转化为数量上不同的生产价格，故劳动价值论不是像某些人所说的那样只适合于简单商品经济，它同样也适合于以利润平均化为重要特征的现代市场经济。

［1］［2］［15］ 马克思：《资本论》，第3卷，北京，人民出版社，2004。

［3］［12］ Bortkiewicz，L.v.“On the Correction of Marx's Fundamental Theoretical Construction in the Third Volume of Capital”.In P.M.Sweezy（ed.）.KarlMarxandtheCloseofHisSystem.New York：A.M.Kelley，1949.

［4］ Winternitz，J.“Value and Price：A Solution of the So－Called Transformation Problem”.EconomicJournal，1948，58 （230）.

［5］ Meek，R.StudiesintheLaborTheoryofValue.New York：Monthly Review Press，1956.

［6］ Seton，F.“The‘Transformation Problem’”.ReviewofEconomicStudies，1957，24 （3）.

［7］ Samuelson，P.A.“Understanding the Marxian Notion of Exploitation：A Summary of the So－Called Transformation Problem between Marxian Values and Competitive Prices”.JournalofEconomicLiterature，1971，9 （2）.

［8］ Foley，Duncan K.“The Value of Theory，the Value of Labor Power，and the Marxian Transformation Problem”.ReviewofRadicalPoliticalEconomics，1982，14 （2）.

［9］ Dumenil，G.“Beyond the Transformation Riddle：A Labor Theory of Value”.ScienceandSociety，1983／1984，47 （4）.

［10］ Kliman，A.and T.McGlone.“A Temporal Single－System Interpretation of Marx's Value Theory”.ReviewofPoliticalEconomy，1999，11 （1）.

［11］ 冯金华：《价值转形：一个伪问题》，载 《经济评论》，2008 （3）；《不必要的生产价格——再论价值转形是一个伪问题》，载 《经济评论》，2009 （4）；《生产价格会偏离价值吗？——三论价值转形是伪问题、兼评几种偏离系数转形模型》，载 《经济评论》，2010 （3）。

［13］ 丁堡骏：《一个真实的经济学命题和一个伪证的学术否定——评冯金华 〈价值转形：一个伪问题〉》，载《当代经济研究》，2009 （3）。

［14］［16］ 裴宏：《价值转形是伪命题吗？——与冯金华教授商榷以及一点评论》，载 《经济评论》，2011 （1）。

［17］［19］［20］ 冯金华：《一般均衡理论的价值基础》，载 《经济研究》，2012 （1）。

［18］ 张忠任：《百年难题的破解》，北京，人民出版社，2004。