导流板对Savonius型海流发电叶轮的影响分析

宋保维, 杨 莼, 田文龙



导流板对Savonius型海流发电叶轮的影响分析

宋保维, 杨 莼, 田文龙

(西北工业大学 航海学院, 陕西 西安, 710072)

Savonius型叶轮是应用最广泛的海流发电叶轮之一, 其成本低、自启动性较好, 但是发电效率较低。为了提高Savonius叶轮的发电效率, 提出了在Savonius叶片上增加3块导流板的新型垂直轴式叶轮的设计方案。为了探索导流板对叶轮的发电性能影响, 利用商业计算流体力学(CFD)软件FLUENT分析了叶轮在不同旋转速度下的发电特性, 采用滑移网格技术对叶轮进行了2D非定常数值流体计算, 分析了在工作环境下叶轮的速度场、压力场的基本特点。计算结果表明, 该叶轮在尖速比=0.9时获得最大平均功率系数0.481, 其发电效率大约比Savonius叶轮高10%～20%左右。

垂直轴式叶轮; Savonius叶轮; 导流板; 滑移网格; 计算流体力学

0 引言

Savonius叶轮是应用最广泛的垂直轴式叶轮之一。Kamoji M A等对Savonius叶轮几何参数对叶轮性能及静力矩效率的影响作出分析[1]; Afungchui D等从理论方面对Savonius叶轮的非线性瞬态势流进行了研究, 并对其流体动力进行了预测[2]; Saha U等通过水洞试验对Savonius叶轮的结构参数进行了优化设计[3]; Shigetomi A等研究了2个Savonius叶轮之间的干扰问题[4]; Golecha K等对安置在Savonius叶轮上产生最大功率的导流板的最佳位置问题进行了研究[5]; Mohamed M等对导流板进行了优化设计[6]。

本文提出利用导流板增加Savonius叶轮效率的设计方案, 分别针对两叶片Savonius叶轮和导流板结合的新型叶轮, 研究了叶轮旋转速度对叶轮发电性能的影响, 分析了其在工作环境下的速度场、压力场和流场的基本特性, 为海流发电装置优化设计提供理论参考依据和必要数据。

1 导流板设计

如图1所示, 3块导流板分别设置在Savonius叶片周围, 垂直于叶轮中心, 导流板之间间隔120°。

图1 新型垂直轴式叶轮示意图

2 计算模型

2.1 物理模型简化

由于采用直叶片, 可以忽略叶片沿径向变形的影响, 从而选用展长为500 mm的Savonius叶片和板长为500 mm的导流板进行2D数值仿真分析。在数值计算过程中, 为降低计算量而又不影响计算精度, 去掉对数值计算不必要的结构特征, 仅保留叶片部分。

图2为垂直轴海流发电装置在来流冲击下以角速度匀速转动的情形, 叶片绕中心轴转动。2D简化结构主要参数如表1所示。

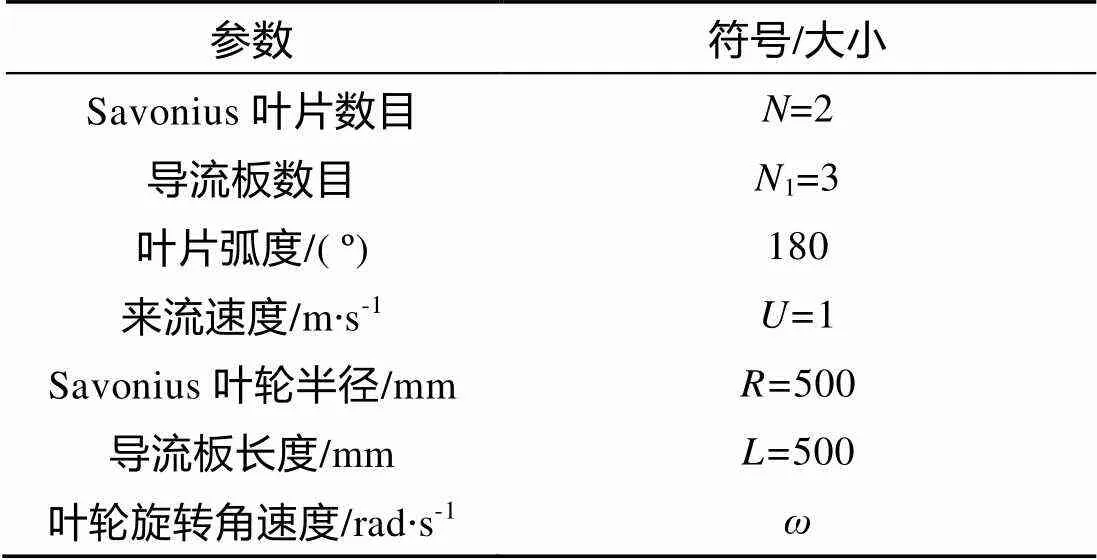
表1 新型垂直轴式叶轮装置简化结构主要参数

图2 2D计算简化结构示意图

2.2 计算域选取及边界条件设置

如图3所示, 计算域由外部静止域(station domain)和内部旋转域(rotating domain)组成, 叶片包裹于旋转域内。为了让来流发展充分并避免由于计算域过小而对计算结果产生误差, 计算域采用半圆与矩形结合的方式, 叶轮装置上游的半圆半径为3倍叶轮直径, 叶轮装置下游长度和宽度均为6倍叶轮直径。

2.3两组患者不良反应发生情况比较 观察组出现失眠1例,心动过速1例,嗜睡2例,不良反应发生率为10.81%;对照组出现低血压2例,心动过速1例,便秘1例,嗜睡1例,体质量增加3例,血糖升高3例,不良反应发生率为29.73%;两组比较差异有统计学意义(X2=4.097,P=0.043<0.05)。

图3 计算域和边界条件设置

Fig. 3 Computation domain and boundary condition

计算区域的边界: 静止域与旋转域的交界设为滑移交界面边界(interface), 半圆入口边界设为速度入口边界(velocity_inlet), 出口边界设为自由流出口(outflow), 上下静止域边界设为滑移壁面边界(wall), 叶片边界均设为滑移壁面, 并在旋转域设定旋转角速度。

2.3 网格生成

本文利用GAMBIT软件完成计算域网格划分工作。由于结构化网格具有占有内存少的优点, 且对边界层计算非常有利, 所以对静止域和旋转域均采用结构化网格, 并在叶片和导流板上进行局部加密, 以提高计算精度。整体网格数量约为30 000。网格划分如图4和图5所示。

图4 静止域网格划分

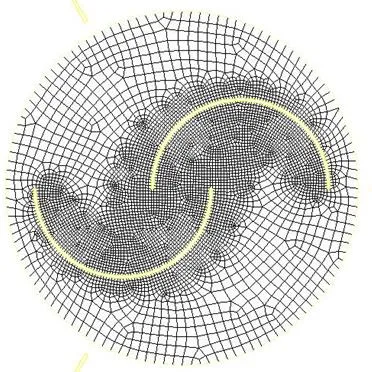
图5 旋转域网格划分

2.4 控制方程及湍流模型

流动问题都必须满足质量守恒定律和动量守恒定律, 按照定律可以提出相关的质量守恒方程与动量方程(-方程)

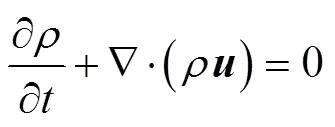
计算基于Standard模型, 与和对应的运输方程为

Standard-模型适用于涉及快速应变、中等涡、局部转换的复杂剪切流动, 在旋转机械的旋转流场计算情况下有较高的可信度和精度。

2.5 求解设置

本文用数值方法直接求解2D不可压粘性流体的RANS方程, 微分方程的离散采用基于单元中心的有限体积法, 非平衡壁面函数的近壁面处理和2D稳态分离解法的隐式解法。在控制方程的离散格式选择上, 压力插值采用便于计算的Standard格式, 压力速度耦合使用计算量较小易于收敛的SIMPLE算法。为了提高计算精度, 减小计算结果的偏差, 动量方程、紊动能方程和耗散率方程均采用2阶迎风格式。

每种工况下计算5个旋转周期, 每个旋转周期设定180个时间步, 即每时间步长内旋转域转动2 º。每个时间步长内迭代100次。流场的连续性、和方向的分量紊动能方程及耗散率的残差收敛标准设为1×10-5。

2.6 数值方法验证

为验证本文数值方法的有效性, 对常规两叶片Savonius风力发电机叶轮进行数值仿真计算, 如图6所示, 计算不同旋转速度时所受平均力矩, 通过对比本文仿真计算结果和试验数据以验证本文数值计算方法的有效性。叶轮详细几何参数及来流速度见文献[7]。

图6 两叶片Savonius叶轮截面图

将计算结果和Hayashi T等所做的风洞试验结果进行了对比[7], 结果如图7所示。分析可知, 本文数值仿真计算结果与试验结果较为吻合, 尤其是当时。仿真结果总体上略高于试验结果, 这可能是因为采用2D数值计算并未考虑壁面影响以及3D叶片叶尖的损失。

图7 仿真结果与风洞试验结果对比

3 计算结果与分析

对叶轮分别进行了2D定常和非定常计算。为消除尺寸影响, 便于分析, 定义如下无量纲系数。

尖速比系数

力矩系数

功率系数

式中:为叶轮旋转速度;为来流速度,=1 m/s;为水流密度,1000kg/mm2;为叶轮半径,500mm;为叶轮特征迎风面积, 定义2, 在2D计算时=1 m。

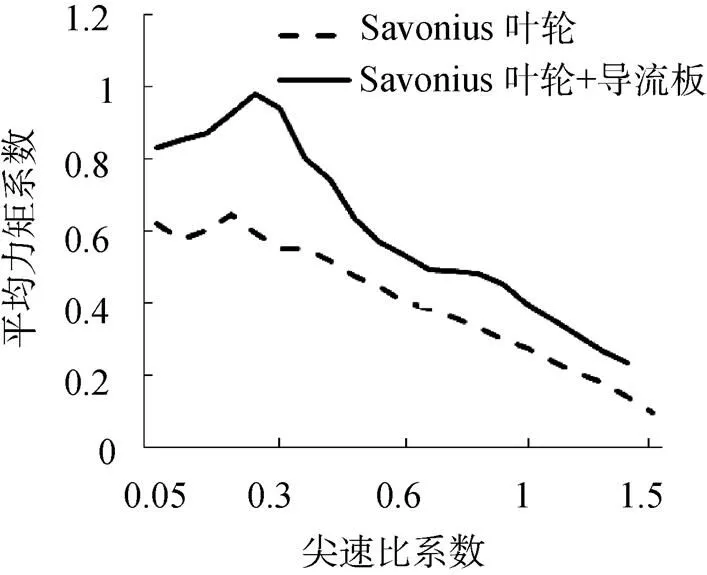
保持来流速度恒定, 对尖速比系数0.05, 0.1, 0.15, …, 1.5的30种情况进行了计算。周期内叶轮平均力矩系数随的变化关系见图8。当=0.3时, 平均力矩系数出现最大值; 随着的增加, 平均力矩系数逐渐下降。与未增加导流板的Savonius叶片对比, 平均力矩系数有了较大提高。

为0.5, 0.7, 0.9和1.1这4种情况下单叶片的力矩系数随旋转位置的变化关系如图9所示。从图中可以看出, 当0.9时,越大, 叶片力矩系数曲线越高; 当0.9时,越大, 叶片力矩系数曲线越小。随着的增加, 力矩系数先增加, 在30°附近出现最大值, 随后力矩系数剧烈下降, 在=140°附近出现最小值。叶片力矩系数在=[90°, 140°]的区间内出现小幅波动。在>140°的范围内, 不同对应的力矩系数曲线差别不大, 呈上升趋势。