高速叶轮的塑性变形特性分析

高 兴, 黄 科, 段 浩



高速叶轮的塑性变形特性分析

高 兴, 黄 科, 段 浩

(中国船舶重工集团公司第705研究所 昆明分部, 云南 昆明, 650118)

为了研究叶轮在高转速工况下所产生的变形特性, 对实际超速试验中采用的叶轮进行了合理的抽象和简化, 利用所建立的物理模型定量分析了叶轮发生塑性应变的范围, 得到了叶轮在给定转速下发生变形的弹性区域和塑性区域, 以及在给定转速下应力和变形的解析解。将所得的应变结果与超速试验的数据进行比较, 误差约为6%, 说明用于该模型的定量计算方法能够有效模拟实际叶轮的变形, 进而给定量分析不同加载转速下的叶轮变形提供了理论依据, 并通过研究叶轮的弹塑性区域, 对叶轮易发生塑性变形的区域进行加强处理, 为叶轮的设计提供参考。

叶轮; 高转速; 变形特性; 超速试验

0 引言

叶轮在转动过程中承受由角速度引起的离心力是叶片和轮盘设计和强度计算中必须着重考虑的问题。此外, 离心力还是影响叶片和轮盘振动的重要因素。国内外学者对叶轮叶片在振动过程中的离心力和变形进行了系统研究[1-3]。朱宝山等从旋转圆盘的理论分析出发, 得到叶轮在弹塑性状态时的应力场、位移场及残余变形场的理论解[4]; Howard D G等研究了离心力和科氏力场中旋转叶片和转轴的结构优化[5]; 张虹等对车用涡轮增压器压气机叶轮进行了强度计算与分析[6]; 陈山等对所设计的几个具有不同几何尺寸的离心压气机叶轮的强度性能进行了计算[7]; 吴荣仁等用弹塑性有限元法分析了超速预过载处理后叶轮的残余位移、应变及应力场, 得出了求解结果[8]; 岂兴明等在单独考虑叶轮离心力的影响下改进了计算的数学模型[9]; Kypuros J A等建立了一个叶轮叶片在转动过程中计算叶顶间隙的简化模型[10]。

本文根据经典力学的相关理论建立了叶轮在离心力作用下的线性及非线性变形模型, 对动力系统叶轮在超转速下的变形进行了定量计算, 并把所得结论与实际超速试验中叶轮的变形量进行了对比, 分析方法和得出的结论可以为研究叶轮在超高转速下的变化规律提供定量分析的理论依据。

1 建立计算模型

在确保叶轮结构性能的前提下, 对叶轮叶片(见图1)作如下基本条件假定与必要的简化。

1) 由于超速旋转试验是在真空条件下进行, 忽略整个系统与外界热交换;

2) 叶轮使用的材料为线性硬化弹塑性材料。

图1 叶轮叶片

2 叶轮在离心力作用下的变形

2.1 完全弹性状态下应力和叶轮变形的理论解

2.1.1 建立单元体受力模型

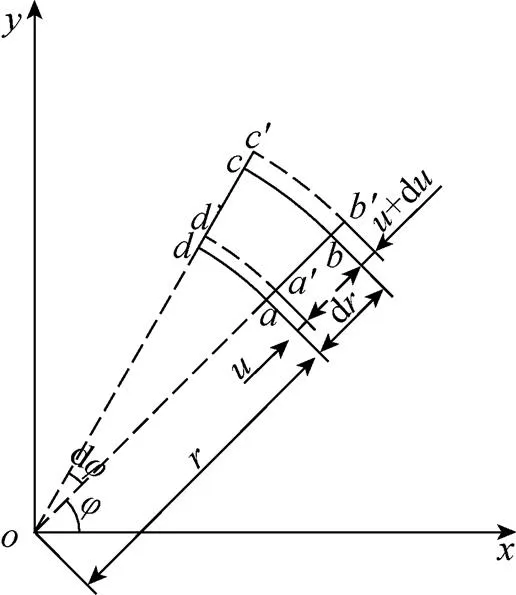
图2 盘面单元体

图3 单元体径向受力图

由图3单元体的受力情况建立径向平衡方程

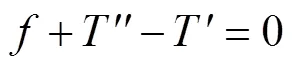
从而可得

(4)

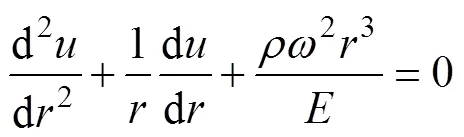
对上式积分, 得到通解为

进而可以求得应力为

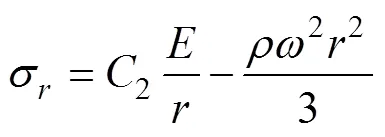
2.1.2 叶片受力分析

在图4中, 由于是直叶片, 在不同高度下的截面积变化可忽略, 故将叶片看作是等截面叶片。

图4 叶片受力分析图

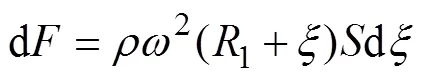
则叶根距为的截面以上段的受力为

在叶片叶根处

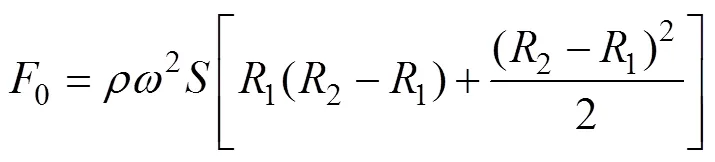
2.1.3 根据边界条件确定位移通解表达式

根据上两式可求得位移表达式

应力为

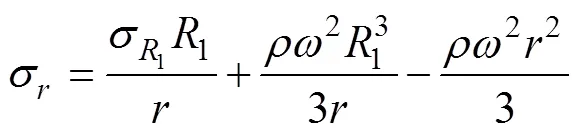
2.2 确定叶轮弹塑性变形区域

图5 叶轮弹性与塑性区

2.3 叶轮变形解析解

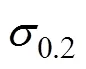
图6 应力应变曲线

因而, 应力应变间的关系简化为

进而重新得到塑性区内单元体径向平衡方程

略去高阶微量, 得到

其通解为

径向应力为

则求得变形量

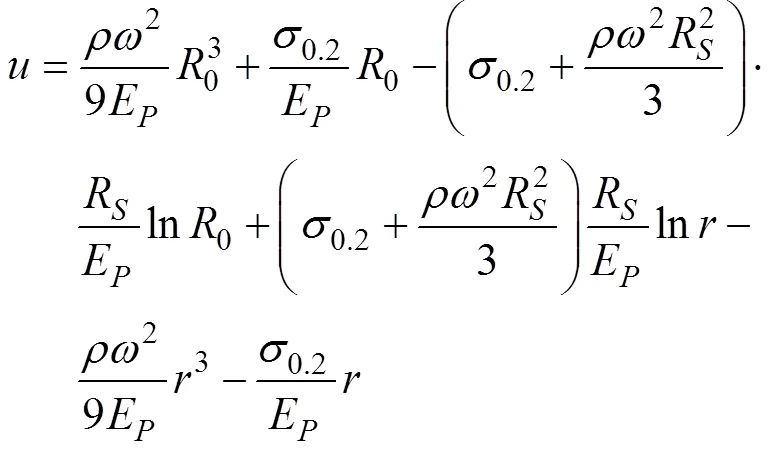
如图7所示, 叶轮盘面的残余变形为

通过上述经典力学对叶轮叶片在特定转速下变形量的分析及计算, 可得到叶轮超速试验结束后叶轮叶片的塑性变形量解析解

3 实例分析

在实际使用中, 叶轮叶片承受离心力和气流力的复合作用, 但气流力对叶片的应力和变形的贡献极其有限。如图8和图9是叶片在某典型工况下, 转速为13 900 r/min时的应力状况。在此工况下, 气流力引起的最大应力为11.0 MPa, 而由离心力和气流力共同作用引起的复合应力为153.2 MPa。由此可见, 此涡轮叶轮中的叶片所受应力主要由离心力导致, 气流力的贡献较小。

图8 叶片只受气流力时应力分布(转速: 0 r/min)

图9 叶片受离心力和气流力时应力分布(转速: 13900 r/min)

试验用叶轮及变形情况如图10和图11所示。在图11中可以清晰地看到, 由于离心力的作用, 叶轮产生了鱼鳞状的塑性变形。

把叶轮在进行50 000 r/min超速试验后的实测变形量2.33 mm和理论计算结果2.48 mm进行比较, 误差约6%。说明用于该模型的定量计算方法能够有效地模拟实际叶轮的变形, 理论分析计算结果和实际变形之间的误差来源, 一部分是由于忽略了环向应力投影在径向上的微小分量, 另一方面则是由于在计算高转速下的变形量时把材料简化为“弹-线”性强化材料所导致。

图10 超速试验中的叶轮

图11 叶轮产生的塑性变形

4 结束语

经过适当简化与假定, 借助于材料力学及弹塑性力学应力应变分析方法, 得到了叶轮盘在给定转速下发生弹性变形和塑性变形区域的解析解, 所得到的结果也为分析涡轮机叶轮在不同区域内强度及应变性能提供了分析方法。

通过所建立的模型, 分别得到了离心力作用下叶轮的变形及卸载后的残余变形量。将该结果与50 000 r/min超速试验的实测结果进行对比后发现, 用该模型来模拟实际叶轮的弹塑性变形是合理的, 误差约6%。

根据理论分析及试验结果表明, 当轮盘发生大范围的塑性变形以后, 叶轮残余变形的大小主要决定于转速的大小及材料的线性强化模量。

[1] Feng J, Benra F K, Dohmen H J. A Study on Impeller-diffuser Interactions in a Radial Pump[C]//Proceeding of the 7thEuropean Conference on Turbomachinery, Fluid Dynamics and Thermodynamics, Athens, Greece, 2007: 773- 782.

[2] 房友龙, 刘永葆, 贺星. 离心力作用下涡轮转子的径向变形[J]. 舰船电子工程, 2011, 31(2): 177-180.Fang You-long, Liu Yong-bao, He Xing. Study of the Radial Elongations of the Turbine Rotor with the Centrifugal Effect[J]. Ship Electronic Engineering, 2011, 31(2): 177-180.

[3] Liang Q W, Wang Z W. Strength and Vibration Analysis of a Francis Turbine[J]. Journal of Tsinghua University(Science and Technoly), 2003, 43(12): 1649-1652.

[4] 朱宝山, 侯炳麟, 张蓉蓉. 超速叶轮的弹塑性分析[J]. 北方交通大学学报, 1998, 22(1): 51-55.Zhu Bao-shan, Hou Bing-lin, Zhang Rong-rong. Elasto- plastic Analysis of Overspeed Impeller[J]. Journal of Northern Jiaotong University, 1998, 22(1): 51-55.

[5] Howard D G, Williams J A. Structural Optimization Incorporating Centrifugal and Coriolis Effects[J]. AIAA Journal, 1991, 26(10): 1743-1750.

[6] 张虹, 马朝臣. 车用涡轮增压器压气机叶轮强度计算与分析[J]. 内燃机工程, 2007, 28(1): 62-66.

[7] 陈山, 杨策, 杨长茂, 等. 几何参数对离心叶轮强度和气动性能影响的研究[J]. 流体机械, 2012, 40(3): 21-26.Chen Shan, Yang Ce, Yang Chang-mao, et al. Investigation of Geometrical Parameters Influence to the Stress and Aerodynamic Performance of Centrifugal Impeller[J]. Fluid Machi- nery, 2012, 40(3): 21-26.

[8] 吴荣仁, 宣海军, 洪伟荣, 等. 涡轮增压器叶轮超速预过载处理技术的研究(1)­——超速预过载叶轮残余变形场分析[J]. 内燃机学报, 2002, 20(3): 53-56.Wu Rong-ren, Xuan Hai-jun, Hong Wei-rong, et al. Research on Pre-Loading Spin Testing of Turbine Supercharger Impeller (1)——Residual Field Analysis of Pre-Over Loading Impeller [J]. Transactions of Csice, 2002, 20(3): 53-56.

[9] 岂兴明, 朴英, 曹志松, 等. 涡轮叶顶间隙数值仿真[J]. 计算机仿真, 2008, 25(6): 42-45.Qi Xing-ming, Piao Ying, Cao Zhi-song, et al. The Numerical Analysis Program of the Tip Clearance of HPT[J]. Computer Simulation, 2008, 25(6): 42-45.

[10] Kypuros J A, Melcher K J. A Study on the Requirements for Fast Active Turbine Tip Clearance Control Systems[C]//Joint Propulsion Conference and Exhibit. Florida: JPCE Press, 2004.

[11] 杨桂通, 树学锋. 塑性力学[M]. 北京: 中国建材工业出版社, 2000.

[12] 朱浩川, 姚谏. 不锈钢材料的应力-应变模型[J]. 空间结构, 2011, 17(1): 62-69.Zhu Hao-chuan, Yao Jian. Stress-strain Model for Stainless Steel[J]. Spatial Structures, 2011, 17(1): 62-69.

Analysis of Plastic Deformation Characteristics for High-speed Impeller

GAO Xing, HUANG Ke, DUAN Hao

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

This paper establishes a physical model of a high-speed impeller for excessive speed test with reasonable abstraction and simplification to quantitatively analyze the plastic deformation range of the impeller. As a result, the analytical solutions of the stress and deformation at given rotary speed as well as the elastic and plastic deformation areas are obtained. Comparison between the stresses fromthe excessive speed tests and from the calculation shows an error of 6%, demonstrating the present method can be used for quantitatively analyzing the deformation of various impellers at different rotary speeds to provide a reference for impeller design.

impeller; high rotary speed; deformation characteristic; excessive speed test

TJ630.32

A

1673-1948(2013)01-0048-06

2012-07-26;

2012-09-04.

高 兴(1986-), 男, 在读硕士, 主要研究方向为水下发射技术.

(责任编辑: 陈 曦)