悬臂薄板结构阻尼特性几种测试方法的比较
李 晖,孙 伟,张永峰,韩清凯
(1.东北大学 机械工程与自动化学院,辽宁 沈阳 110819;2.大连理工大学 机械工程学院,辽宁 大连 116024)
在振动和噪声控制中,阻尼的测试有着重要的工程及学术意义,阻尼参数是振动计算分析时必须输入的关键参数之一,不仅可用于结构动力学的建模、响应预估和优化设计等环节,还可以用来评价和校验阻尼减振效果.随着阻尼减振技术的广泛应用,结构系统的阻尼测试技术显得越发重要.
目前,学者们[1-5]对阻尼测试方法的研究非常活跃.但是,由于机械结构系统阻尼机理的复杂性,例如,系统的阻尼可能要受到材料性质、边界约束条件、环境温度、激励振幅以及结构变形等多种因素的影响,使阻尼的测量具有很大程度的不确定性.到目前为止,学术及工程界尚未建立一种完备而有效的阻尼评价与测试方法.在阻尼测试的实践中,经常出现精度低、可重复性差及测试效率低下的缺陷,因此,关于阻尼测试的研究还应进一步深入.
目前,关于阻尼测试所提出的方法各有不同的优缺点.本文认为对于具体的结构,要在明确阻尼表征参数的基础上,选择一种合适的阻尼测试方法,这样才能有效对机构系统的阻尼性能进行评价.本文首先简单介绍了阻尼识别的几种最常用的方法,然后应用这几种方法,针对悬臂薄板结构,搭建了三种不同激励形式(锤击、振动台、压电陶瓷激振)的测试系统,分别采用半功率带宽法和时域自由振动衰减法,对薄板的阻尼特性进行了辨识.并从可重复性、测试精度等方面,将各种测试结果进行了详细比较,得到了有价值的结论,为后续的响应预估和阻尼优化设计提供了重要的参考数据.
1 阻尼测试的基本原理
1.1 用于描述结构系统阻尼特性的参量
阻尼是反映结构系统振动过程中能量耗散特征的参数,其本质是振动系统能量的转换,即从机械能转换为热能或其他能量形式的过程[6].用于描述结构的阻尼的参量有很多,例如:相位差角φ、对数衰减系数δ、品质因子Q、损耗因子η、阻尼比ζ等,在小阻尼情况下,各个参量之间有如下关系[7]:

在动力学分析及振动性能评价中,通常采用阻尼比ξ或损耗因子η来描述结构系统的阻尼.由于其应用方便,数学概念清晰,因此,本文采用阻尼比来描述被测结构的阻尼.
1.2 频域阻尼测试方法
常见的频域法有半功率带宽法、频率细化法、峰值法、导纳圆法等[8].在工程实际中,半功率带宽法由于其原理简单,操作方便而应用最为广泛.目前比较著名的有比利时LMS公司和丹麦B & K公司的商业化振动测试系统,其阻尼辨识方法均基于半功率带宽法.
半功率带宽法的原理可概括为:获得系统的频域响应的共振峰,然后利用共振频率及共振点附近幅值下降倍的2个频率点来获得系统的阻尼参量,其求解公式可表示为
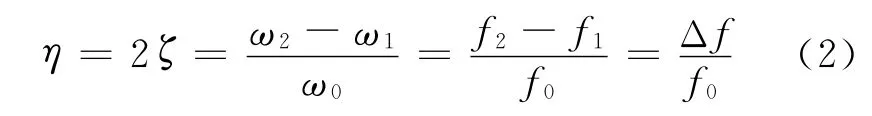
式中:ω0为系统固有角频率,rad·s-1;f0=2πω0,为系统固有频率,Hz;ω1,f1和ω2,f2分别为对应共振峰两侧且幅值为共振峰值倍时的2个角频率和2个频率值.
采用半功率带宽法对结构系统进行阻尼测试的研究十分普遍.例如,美国材料与测试学会[1]标准中就采用半功率带宽法识别涂层材料的阻尼;美国空军大学Ivancic F等[7]利用振动台对钛板进行扫频激励,采用半功率带宽法从响应信号中辨识阻尼.
1.3 时域阻尼测试方法
时域阻尼测试方法有自由振动衰减法、Ibrahim时域法(ITD法)、节约时间法(STD法)、随机减量法等[9].其中自由振动衰减法是时域测量系统阻尼的一种经典方法.该方法首先对系统实施一个脉冲或稳态激励,激励停止后系统做自由振动,通过检测自由振动衰减的速度,来确定系统的阻尼.
以下以单自由度系统为例加以说明,有阻尼单自由度系统的衰减响应可表达为

式中:A为振幅;t为衰减时间;φ为相位差角.其衰减响应曲线见图1,对数衰减系数δ可表示为

式中:A1,A2分别为相邻的两个振动周期内的振幅.
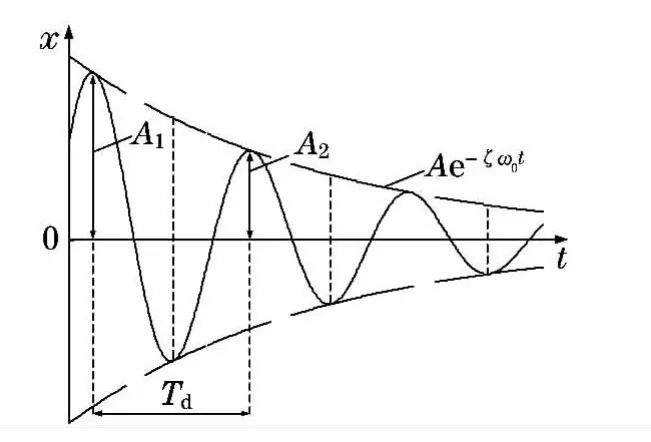
图1 单自由度振动系统时域响应曲线Fig.1 Time response of one-degree-freedom system
自由振动衰减信号的包络线法是自由振动衰减法的进一步扩展.由公式(3)可知单自由度振动位移衰减信号的包络线方程和拟合曲线方程分别为

式中,a,b,c分别为拟合曲线的常系数.
参考式(5),位移衰减信号的阻尼辨识公式可用式(7)表示,加速度和速度信号的识别公式也类似.

一般结构往往是多自由度系统,但按照模态理论解耦后可变成若干单自由度系统.每个单自由度系统描述了结构在某阶固有频率下共振时的运动状态.因此,可用自由振动衰减法辨识结构的各阶模态阻尼比.
学者们应用自由振动衰减法来辨识结构系统的阻尼的例子也不胜枚举,FILIPE M等[10]采用自由振动衰减法测试桥梁结构的阻尼特性,并与脉冲激励结果进行了对比.BOTELHO E等[11]也利用自由振动衰减法测试铝合金、碳纤维等材料的阻尼比.国内的卢晓东等[12]还研究了包括自由振动衰减法在内的三种时间响应阻尼识别方法,认为自由振动衰减法不适用于信噪比较低的情况下的阻尼识别.
虽然在时、频域上测试阻尼的方法多种多样,阻尼辨识原理也比较明确.但面向特定测试对象所搭建的不同测试系统,例如,激励形式、激振频率范围以及响应信号的采集方法等(如传感器位置、重量及接触形式)都会对阻尼的辨识结果有很大程度的影响.因此,本文认为对于一个具体的结构系统,需要根据具体的结构特点来组建测试系统,并采用最佳的阻尼测试方法获得其阻尼特性.
2 悬臂薄板结构阻尼测试的几种方法
本文面向悬臂薄板结构,按激励和阻尼辨识方式的不同,可以分为以下4种阻尼测试方法.
2.1 锤击脉冲激励-频域测试阻尼
采用锤击法测试阻尼所组成的试验系统见图2.其测试流程可概括为:利用模态力锤获得力信号,轻质加速度传感器获得响应信号;用响应信号除以力信号获得频响函数;再通过半功率带宽法由频响函数识别各阶固有频率和对应的阻尼比.图3为锤击法获得的频响函数.

图2 锤击脉冲激励图Fig.2 Photo of damping test

图3 锤击频响函数图Fig.3 FRF measured by hammer
2.2 压电陶瓷宽带随机激励-频域测试阻尼
压电陶瓷是一种可提供10~20kHz频段内激励信号的一种高频激励设备.压电陶瓷激励测试阻尼的实验系统见图4.其测试流程可概括为:用压电陶瓷对薄板进行随机激励并记录激励信号,用轻质加速度传感器记录响应信号;接着对激励和响应信号进行处理获得频响函数;最后同样通过半功率带宽法获得各阶模态阻尼比.图5为压电陶瓷激励获得的频响函数.

图4 压电陶瓷激励图Fig.4 Photo of damping test by piezoelectric ceramic exciter
2.3 振动台扫频激励-频域测试阻尼
振动台扫激励-频域测试阻尼的试验系统见图6.其测试方法可概括为:用振动台以基础激励的方式对悬臂薄板结构进行定幅扫频激励,扫描频段可以选择为某阶固有频率的75%~125%,在此频段内以能够有效消除瞬态振动的扫频速度进行扫频测试(通常小于1Hz·s-1);用轻质加速度传感器进行响应信号的采集,并对时域原始数据进行分时段FFT变换处理,获得每个微小时段的频域响应峰值,再将其投影到同一频谱图上,获得扫频激励的频域响应图;最后,用半功率带宽法识别阻尼.图7为经分时段FFT变换得到的薄板指定点的频域响应.用包含不同阶次固有频率的扫频信号激励试件,则可获得各阶阻尼比.

图5 压电陶瓷激励频响函数图Fig.5 FRF measured by piezoelectric ceramic exciter

图6 振动台激励实验系统Fig.6 Photo of damping test by vibration shaker exciter
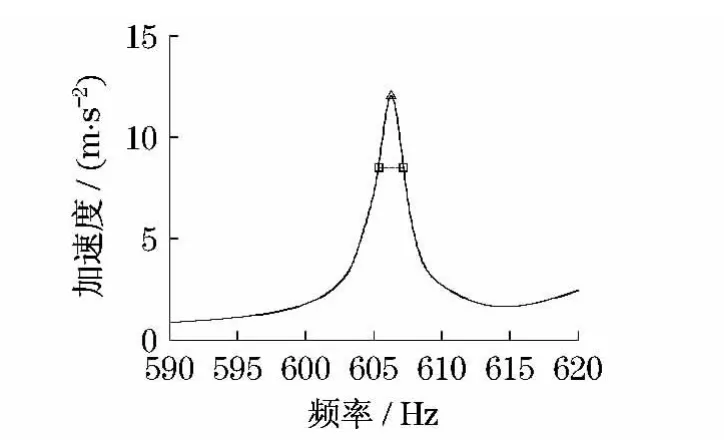
图7 分时段FFT变换得到的第5阶频域响应Fig.7 5th frequency response through FFT of different periods of time
需要说明的是,这里用于识别阻尼的是频域响应,而不是频响函数,按振动学理论,也可由频域响应辨识阻尼.仍以单自由度系统为例加以说明,基础激励下稳态响应的振幅为
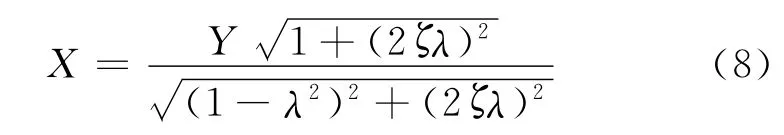
式中:X为结构件的响应幅度;Y为基础激励的幅度;λ为激振频率与固有频率之比,λ=ω/ω0.
[5][7] Rex W. Tillerson, Remarks on “Defining Our Relationship With India for the Next Century”, Center for Strategic and International Studies, Washington DC, October 18, 2017, https://www.state.gov/secretary/remarks/2017/10/274913.htm.
振幅最大值为

在ω0左右取两个频率点ω1,ω2,且所对应的频域响应幅值相等,即X1=X2,X1,X2与振幅最大值Xmax的比值为r(0<r<1),即X1=X2=rXmax,则有
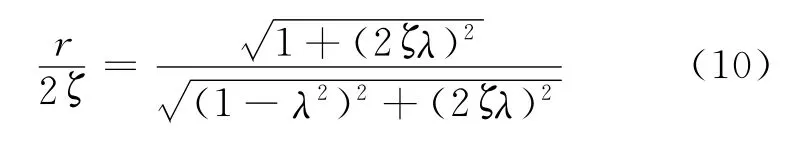
对应的两个频率点可表示为
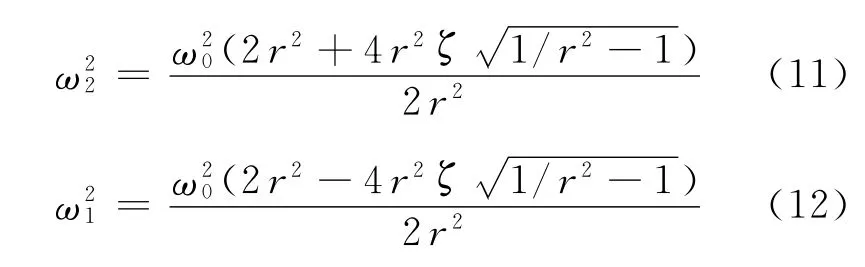
两个解的平方相减得

即
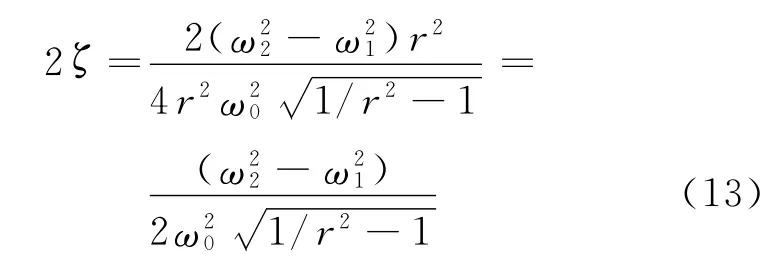


2.4 振动台定频共振激励-时域测试阻尼
振动台基础共振激励测试阻尼的试验系统与图6相同.其测试方法可概括为:在精确获得悬臂薄板各阶固有频率的基础上,用振动台以共振频率定频、定幅激励薄板结构;待达到稳态响应后,持续2s以上,然后停止激励,并用轻质加速度传感器测量稳态响应信号和衰减信号;分别用自由振动衰减法或包络线法获得结构的阻尼比.图8为测试薄板获得的第1阶自由振动衰减信号.用不同阶次的固有频率激励结构,则可获得各阶阻尼比.
3 悬臂薄板结构阻尼测试结果比较
悬臂薄板见图2,材料为TC4钛合金.该薄板的长、宽、厚度分别为152mm,110mm,1mm,薄板处于悬臂状态,夹持区为40mm,采用上述4种方法进行阻尼测试,涉及的仪器见表1.
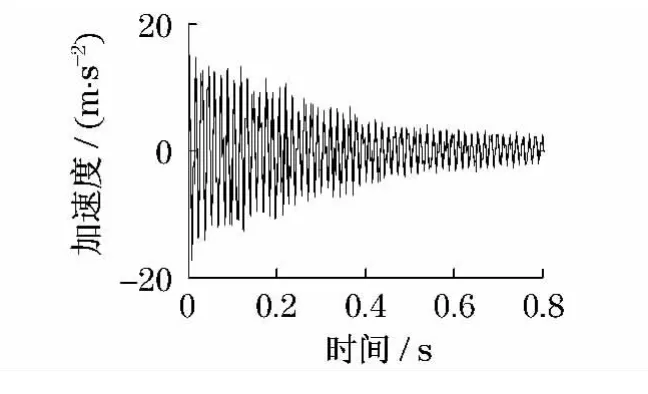
图8 薄板第1阶自由振动衰减信号Fig.8 Time response of 1st free-vibration attenuation

表1 阻尼测试相关仪器参数Tab.1 Equipments and sensors in damping test
3.1 固有频率测试结果
从上述几种阻尼测试方法中均可以获得悬臂薄板结构的固有频率,测得的固有频率见表2.从表2可知,除了压电陶瓷激励外,各方法获得的固有频率基本一致.由于压电陶瓷本身附加质量的影响,此方法获得的固有频率略低于其他结果.
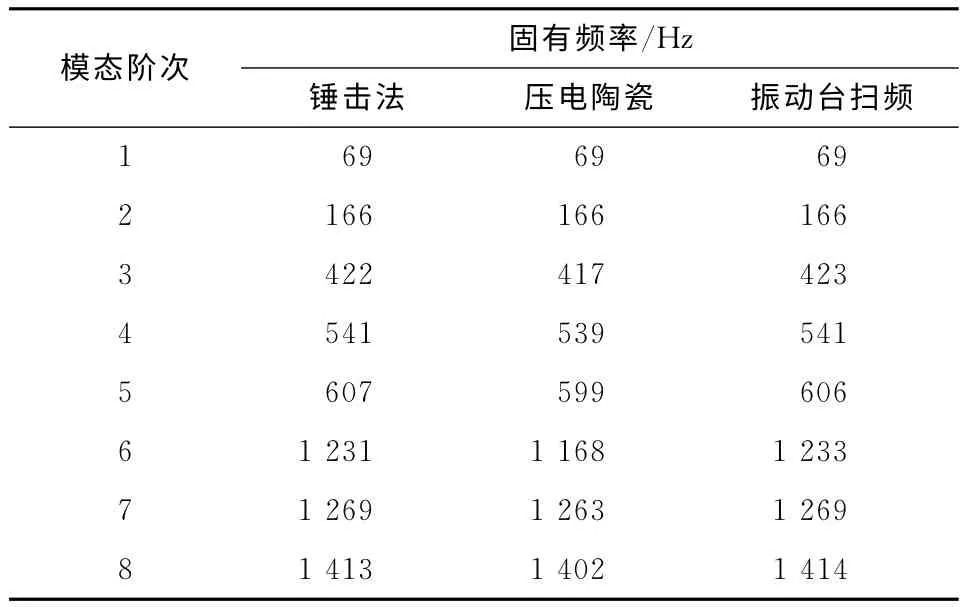
表2 不同激励形式下获得的固有频率Tab.2 Natural frequencies under different excitation form
3.2 阻尼测试结果
为了避免因为传感器位置不同而造成的实验误差,特将各种测试方法的响应测点布置在薄板上相同一点,每阶阻尼比都至少测量3次,然后对各种测试结果进行了深入比较.相应的测试结果见表3至表7.
3.3 结果比较分析
对比各种方法的测试结果可以发现,对于同一薄板结构阻尼测试的结果差异性较大,这正说明了结构系统阻尼机理的复杂性以及阻尼测试的困难性.以下从可重复性、测试精度、测试阻尼的频率范围和测试效率上进行对比说明.
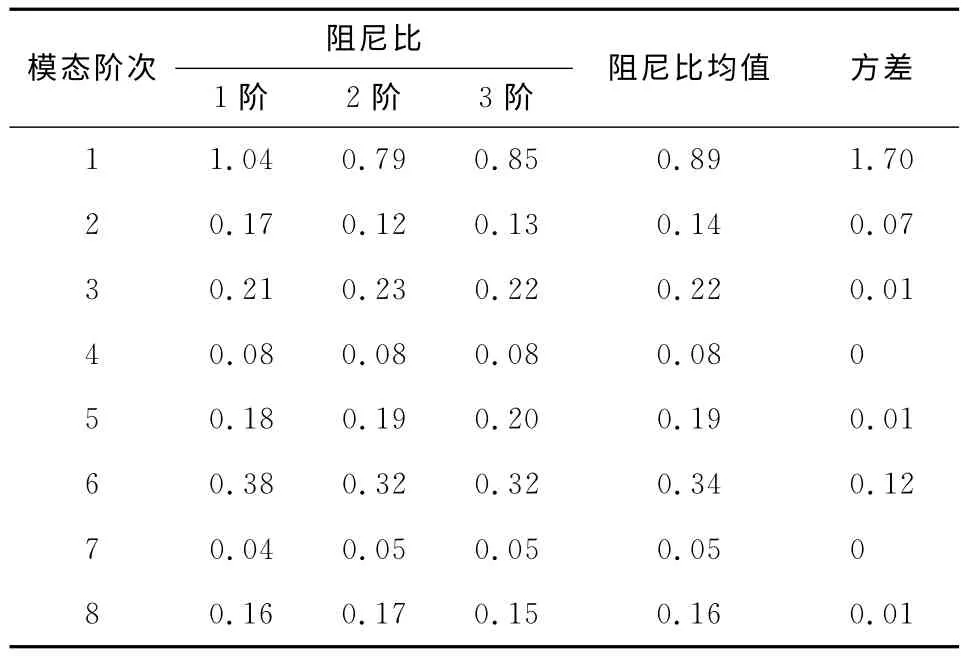
表3 锤击脉冲激励-频域测试阻尼Fig.3 Damping test results by hammer and identified through FRF %

表4 压电陶瓷宽带随机激励-频域测试阻尼Fig.4 Damping test results by piezoelectric ceramic exciter and identified through FRF %
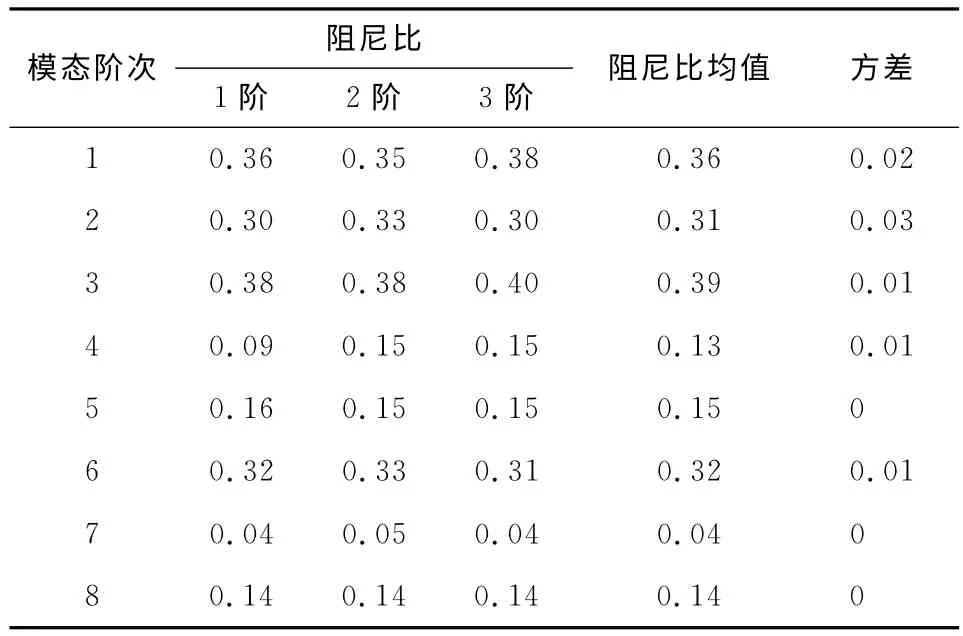
表5 振动台扫频激励-频域测试阻尼Fig.5 Damping test results by vibration shaker exciter and identified through FFT of different periods of time %
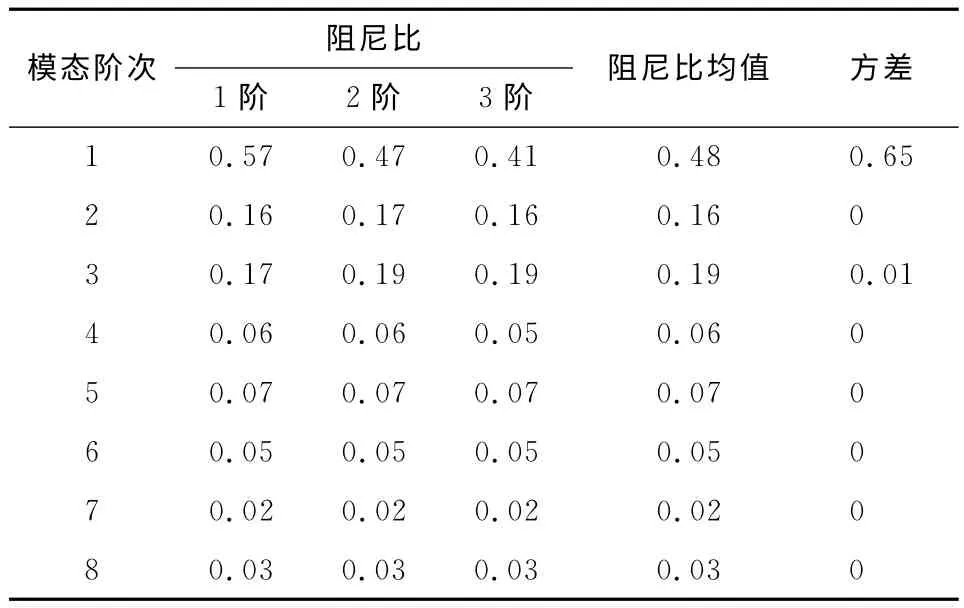
表6 振动台定频共振激励-时域自由振动衰减法测试阻尼Fig.6 Damping test results by vibration shaker exciter and identified through time responses of free-vibration attenuation %

表7 振动台定频共振激励-时域衰减包络线法测试阻尼Fig.7 Damping test results by vibration shaker exciter and identified through envelopes of free-vibration attenuation %
3.3.1 可重复性
按照方差求解式来判定每种测试方法可重复性的优劣,相应的结果同样列在表3至表7中.

式中:S为样本方差;D0为测试样本的平均数;n为样本的数量;Di为每次测试的样本数据.
通过比较各种测试方法的方差值,可以发现锤击法和时域自由振动衰减法对第1阶阻尼识别的可重复性较差,其他阶次以及其他方法可重复性均较好.总体上看,可重复性最好的是振动台扫频激励-频域法测阻尼,对应每个阶次方差均小于0.03%.
3.3.2 测试精度
由图5可知,压电陶瓷低频激励能力有限,该方法获得的频响函数谱图在低阶(200Hz以下)存在较大的干扰成分.因此,其前两阶阻尼测试结果的可重复性较差,由此识别阻尼值存在一定的误差.而振动台激励时域测试阻尼过程中,响应信号容易受到测试环境的干扰.如图8,第1阶自由衰减过程中某些时刻的加速度峰值高于前一时刻,说明信号并非完全的自由衰减.包络线法在第1阶方差值相对较大,也说明此现象.可见,上述方法在相关阶次阻尼比的测量中精度不高.而振动台扫频激励-频域法测试阻尼对应的每个测试过程,均可以得到如图7所示的稳态频域响应信号,由此认为该方法具有很好的测试精度.
3.3.3 测试阻尼的频率范围
压电陶瓷的激振频率可达到20kHz,其本身的结构特性使其在高频段有稳定的频响,因而更加适用于测试高频阻尼.而与振动台激励所相关的频域及时域测试方法,则要受到振动台自身激振能力的限制,通常难以测试高频阻尼.例如,本文所用的振动台,最高仅可以测试2 400Hz频域范围内的阻尼.
3.3.4 测试效率
锤击法测试阻尼最为方便、快捷,硬件成本也最低.压电陶瓷和振动台测试阻尼的硬件成本则相当巨大,测试效率也较低.然而,振动台激励可以准确控制激振力幅和信号类型,易于准确测试和评价某些涂有阻尼减振材料的薄板结构的阻尼特性.
综上,精确评价本文研究的薄板结构的阻尼大小,本文认为宜采用振动台扫频激励方法进行测试.
4 结论
本文针对悬臂薄板结构,搭建了锤击、振动台、压电陶瓷激励三种测试系统.分别采用半功率带宽法和时域自由振动衰减法其阻尼特性进行了测试.经过比较研究发现,通过振动台扫频激励方法获取振动响应,并采用半功率带宽法对分时段傅里叶快速变换(FFT)处理后的频域响应进行阻尼识别的精度最高,该方法更适合精确评价本文所研究的薄板结构的阻尼大小.
[1]ASTM.E756-05standard test method for measuring vibrationdamping properties of materials[S].West Conshohocken:American Society for Testing and Materials,2010.
[2]MASTI R S,SAINSBURY M G.Vibration damping of cylindrical shells partially coated with a constrained viscoelastic treatment having a standoff layer[J].Thinwalled Structures,2005,43(9):1355-1379.
[3]GIBSON R F.Damping characteristics of composite materials and structures[J].Journal of Materials Engineering and Performance,1992,1(1):11-20.
[4]BARBIERI N,NOVAK P R,BARBIERI R.Experimental identification of damping[J].International Journal of Solids and Structures,2004,41(13):3585-3594.
[5]LEE J H,KIM J.Development and validation of a new experimental method to identify damping matrices of a dynamic system[J].Journal of Sound and Vibration,2001,246(3):505-524.
[6]ADHIKARI S,WOODHOUSE J.Identification of damping:part 1,viscous damping[J].Journal of Sound and Vibration,2001,243(1):43-61.
[7]IVANCIC F,PALAZOTTO A.Experimental considerations for determining the damping coefficients of hard coatings[J].Journal of Aerospace Engineering,2005,18(1):8-17.
[8]EWINS D J.Modal testing:theory and practice [M].Letchworth:Research Studies Press,1995.
[9]戴德沛.阻尼技术的工程应用[M].北京:清华大学出版社,1991.DAI Depei.Technical application of damping technology[M].Beijing:Tsinghua University Press,1991.
[10]FILIPE M,ALVARO C,ELSA C,et al.Damping estimation using free decays and ambient vibration tests[J].Mechanical Systems and Signal Processing,2010,24(5):1274-1290.
[11]BOTELHO E,CAMPOS A,DE BARROS E,et al.Damping behavior of continuous fiber/metal composite materials by the free vibration method[J].Composites Part B:Engineering,2006,37(2):255-263.
[12]卢晓东,费庆国,韩晓林.基于时间响应函数的结构阻尼识别方法比较[J].力学与实践,2011,33(2):58-61.LU Xiaodong,FEI Qingguo,HAN Xiaolin.Evaluation and application of damping identification methods based on time response functions[J].Mechanics in Engineering,2011,33(2):58-61.

