两种转子-轴承系统模型的油膜失稳故障仿真
马 辉,李 辉,牛和强,能海强
(东北大学 机械工程与自动化学院,辽宁 沈阳 110819)
随着旋转机械向高转速、大跨度、柔性轻结构方向发展,滑动轴承油膜与转子相互作用所引起的油膜失稳问题日益突出.油膜失稳会使转子系统在同频周期运动的基础上产生较大的低频振动,从而使系统产生非协调进动,使转轴产生较大的交变应力,此外油膜失稳也会造成转子振动加剧,从而可能诱发诸如转定子碰摩等其他故障,因而研究油膜失稳的动力学特征,对于系统的设计以及油膜失稳的故障诊断、防治和消除具有重要的意义.
目前对滑动轴承-转子系统动力学的研究,主要集中在转子系统及非线性油膜力的建模和求解、系统稳定性及非线性动力学特性研究等方面[1-14].有关转子系统的建模方法主要有集中质量法和有限元法,集中质量法考虑自由度较少,计算效率高,一般主要针对简单转子系统;有限元法可以考虑有效几何参数、转子惯量分布效应、内阻尼、剪切效应、弯曲振动和扭转振动的组合效应等,因而具有更高的精度,但是计算效率较低.有关转子系统稳定性的研究,多涉及系统的油膜失稳故障,在实际的转子机组中,为了追求更高的效率,工作转速往往超2阶甚至更高阶临界转速,而对于在超2阶临界转速以上运转的转子系统,根据文献[11]试验结果,有可能会出现2阶油膜振荡,对于高阶油膜振荡的研究目前还很少.
本文主要基于这一实际情况,以某单跨双盘转子系统为研究对象,基于API617标准确定两种危险工况,建立了考虑陀螺影响集中质量模型和有限元模型,滑动轴承采用短轴承非线性油膜力模型,采用Newmark-β数值积分法,基于两种数学模型,分析了不同载荷工况对低阶和高阶油膜失稳的影响规律,对比了两种建模方法的异同点.研究结果可为转子油膜失稳故障机理及故障诊断提供依据.
1 双盘轴承-转子动力学模型
1.1 集中质量模型
图1a为转子结构尺寸示意图,其中左轴承采用自润滑石墨轴承,本文采用弹簧-阻尼来模拟,右轴承为滑动轴承,油膜力采用文献[1]中的短轴承油膜力模型.轴承-转子系统集中质量模型示意图,如1b所示,其运动微分方程具有以下形式:
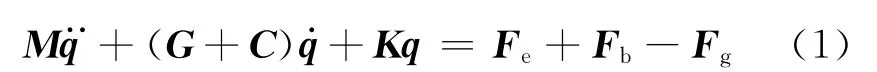
式中:M为质量矩阵;G为陀螺矩阵;C为阻尼矩阵(包括左轴承阻尼);K为刚度矩阵(包括左轴承刚度);q为位移向量;Fe,Fb,Fg分别为轴承不平衡惯性力、轴承油膜力和重力外激励向量.
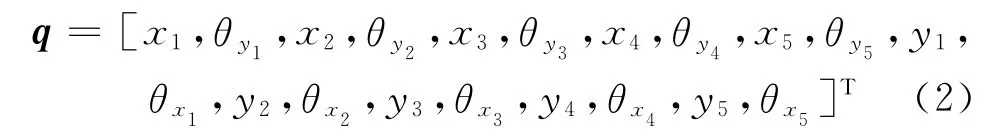
式中:xi,yi,θxi,θyi(i=1,2,…,5)分别为质量点i的x向位移、y向位移、绕x轴转角和绕y轴转角.关于M,G和K的矩阵元素详见文献[15].
为了计算系统振动响应,需要设定系统的阻尼,本文采用比例阻尼形式和轴承阻尼来模拟系统阻尼,其矩阵形式如下:

式中:C1为比例阻尼矩阵;C2为轴承阻尼矩阵.
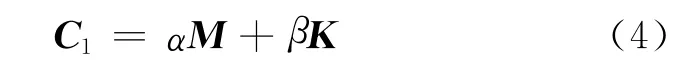
1.2 有限元模型
转子系统采用采用Timoshenko梁来模拟(见图1),根据转子系统结构特征将其分为26个单元,其有限元模型如图1c所示,自润滑石墨轴承和滑动圆轴承分别在节点4和节点26处,转盘位于节点11和节点19处.系统的运动微分方程仍可用式(1)来表示.
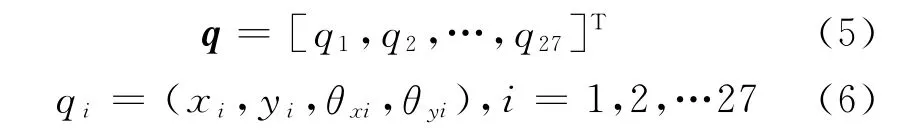
式中:xi,yi和θxi,θyi分别为转子第i个节点沿x向和y向的位移和转角.油膜力仍采用文献[1]中的短轴承油膜力模型,其阻尼形式与集中质量模型相同.关于M,G和K的矩阵参数,详见文献[16].轴承-转子系统的结构尺寸及模型示意图如图1所示.转子简化的集中质量及轴承的有关参数详见表1.图和表中mi,Jpi和Jdi(i=1,2,…,5)分别为集中质量点的质量、极转动惯量和直径转动惯量;η为润滑油黏度;kblx,kbly,cblx和cbly分别为左轴承x向和y向油膜刚度和阻尼,c,D和L分别为滑动轴承间隙、轴承直径和轴承宽度.
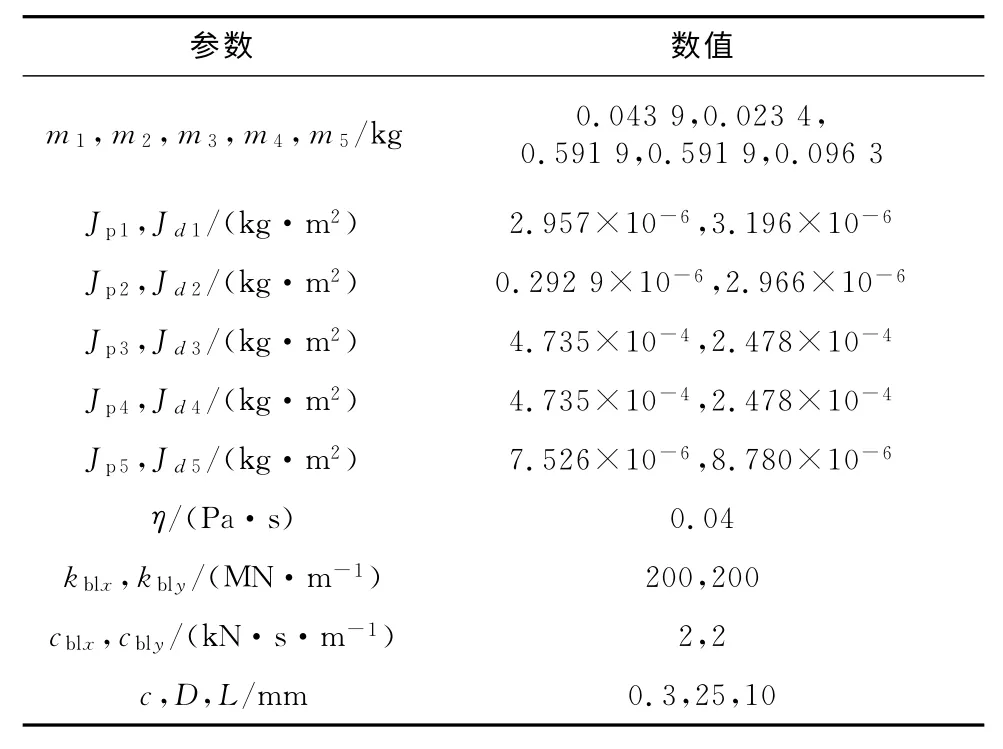
表1 转子及轴承参数Tab.1 Rotor and bearing parameters

图1 轴承-转子系统几何尺寸及模型示意图Fig.1 Geometrical parameters and model schematic diagram of a rotor-bearing system
2 两种数学模型的油膜失稳仿真
根据API617标准,确定两种不同的载荷加载工况,如图1b,c所示.第一种载荷工况为两圆盘激振力同相位,第二种载荷工况为反相位.根据轴承-转子系统结构模型,确定的系统的第1阶和第2阶临界转速分别为1 680r·min-1和6 450r·min-1.

图2 工况1时三维谱图Fig.2 Spectrum cascades of two kinds of mathematical models at condition 1
2.1 载荷工况1下数值仿真
基于集中质量模型,得到质量点5(右轴颈处)在竖直方向(y向)的三维谱图,如图2a所示.当转速为600r·min-1≤n<2 800r·min-1时,转子响应为同步正进动,在三维谱图除了转频fr外还出现了2fr和3fr.当转速为2 800r·min-1≤n≤3 300r·min-1(接近2倍的1阶临界转速)时,系统出现油膜涡动现象,其涡动频率为23.33~27.50Hz.当转速继续增加到3 300r·min-1<n<5 100r·min-1时,由于不平衡力引起的工频成分迅速增大抑制了转子的油膜失稳,油膜涡动现象暂时消失,在此阶段主要存在转频fr,2fr和3fr.当转速为n≥5 100r·min-1时,1阶油膜振荡发生,频率锁定在28.5Hz附近,此时振动能量主要集中于1阶油膜振荡,油膜振荡的幅值迅速增大,工频振动的幅值迅速减小,此转速区间内频率成分主要为转频fr和1阶油膜振荡频率fn1的组合成分.
为了以后便于和试验结果对比,且考虑到右轴承处节点27和节点24较为接近,其振动位移基本一致,所以在有限元方法中只提取了节点24数据进行对比分析,其竖直方向(y向)的三维谱图,如图2b所示.由图可知当转速600r·min-1≤n<2 700r·min-1时,转子响应为同步正进动,频率除了转频fr外还出现了2fr,3fr.当转速为2 700r·min-1≤n≤3 140r·min-1时,系统出现油膜涡动现象,其涡动频率为22.5~25.5Hz.当转速继续增为3 140r·min-1<n<4 200r·min-1时,油膜涡动现象暂时消失,在此阶段主要存在转频fr,2fr和3fr.当转速为n≥4 200r·min-1时,1阶油膜振荡发生,频率锁定在26.54Hz,此时振动能量主要集中于1阶油膜振荡,油膜振荡的幅值迅速增大,工频振动的幅值迅速减小,由于系统的非线性,此转速区间内频率成分主要为转频fr和1阶油膜振荡频率fn1的组合成分.
图3为n=2 800r·min-1时集中质量模型质点5和有限元模型节点24的轴心轨迹和频谱图,由图可知二者轴心轨迹均为内“8”字,从频谱图看,除了有fr,2fr,3fr还出现了1阶油膜振荡频率fn1.图4为转速n=12 000r·min-1时质点5和节点24处的轴心轨迹和频谱图,质点5的轴心轨迹为6个内“8”字,有限元法所得轴心轨迹为9个内“8”字,二者频谱图均表明1阶油膜振荡频率fn1的幅值远高于转频幅值.

图3 在2 800r·min-1时质点5和节点24轴心轨迹和频谱图Fig.3 Rotor orbit and frequency spectrum of mass point 5and node 24at 2 800r·min-1

图412 000r·min-1时轴心轨迹和频谱图Fig.4 Rotor orbit and frequency spectrum of mass point 5and node 24at 12 000r·min-1
2.2 载荷工况1下数值仿真
工况2载荷条件下质点5的三维谱图,如图5a所示.当转速为3 000r/min≤n≤3 900r·min-1时,系统出现了油膜涡动现象,其涡动频率范围为25.00~27.62Hz.当转速继续增加到3 900r·min-1<n<8 700r·min-1时,油膜振荡现象消失,在此阶段主要存在转频fr和2fr.当转速为8 700r·min-1≤n<12 300r·min-1时,1阶油膜振荡发生,频率锁定在27.51Hz,频率成分主要为转频fr和1阶油膜振荡频率fn1的组合成分.当转速为12 300r·min-1≤n≤13 200r·min-1时,第2阶油膜涡动出现,此时fn1幅值开始减小,第2阶油膜涡动频率范围为103.0~105.6Hz.当转速为13 200r· min-1<n<14 100r·min-1时,第1阶和第2阶油膜振荡同时消失.转速继续升高为14 100r·min-1≤n≤16 000r·min-1时,第1,2阶油膜振荡又同时发生,其中第2阶油膜振荡频率锁定在98.1Hz,振动能量在fn1和fn2两个频带上交替变化,主要体现为fn1和fn2的幅值交替升降.
工况2载荷条件下节点24的三维谱图,如图5b所示.当转速为2 700r·min-1≤n≤4 400r·min-1时,系统出现油膜涡动现象,其涡动频率范围为23.63~27.26Hz.当转速继续增加到4 400r·min-1<n<7 000r·min-1时,油膜振荡现象消失,在此阶段主要存在转频fr和2fr.当转速为7 000r·min-1≤n<8 200r·min-1时,第1阶油膜振荡发生,频率锁定在27.3Hz,此时振动能量主要集中于1阶油膜振荡,油膜振荡的幅值迅速增大,转频振动的幅值迅速减小,此转速区间内频率成分主要为转频fr和1阶油膜振荡频率fn1的组合成分.当转速为8 200r·min-1≤n<16 800r·min-1时,第2阶油膜涡动出现,其涡动频率范围为100.2~104.0Hz,但此时的涡动幅值很小.当转速为16 800r·min-1≤n≤19 800r·min-1时,第2阶油膜振荡振幅剧增,其频率锁定在96.7Hz,振动能量在fn1和fn2两个频带上交替变化,主要体现为fn1和fn2的幅值交替升降,此时还出现了连续谱线.
图6为转速n=12 400r·min-1时,质点5和节点24的轴心轨迹和频谱图.由图6可知二者的轴心轨迹均为多个不重合的椭圆,从频谱图看,均出现了前2阶油膜振荡频率fn1和fn2.
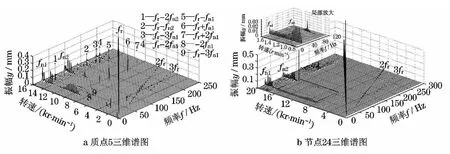
图5 工况2时三维谱图Fig.5 Spectrum cascades of two kinds ofmathematical models at condition 2

图612 400r·min-1时轴心轨迹和频谱图Fig.6 Rotor orbit and frequency spectrum of mass point 5and node 24at 12 400r·min-1
2.3 集中质量和有限元法结果对比
将集中质量法和有限元法求得的两种工况的组合频率特征进行对比,结果如表2所示.
3 结论
本文针对一个单跨双盘转子系统,分别采用集中质量模型和有限元模型,分析了在两种载荷工况下,系统升速过程中出现的油膜失稳故障,得到的主要结论如下:
(1)两种数学模型在两种不同加载工况下,系统的失稳规律类似,均为在工况2时系统失稳转速较高,且均出现了系统第2阶油膜振荡频率.
(2)两种数学模型在工况2时系统涡动频率均较工况1时复杂,主要表现为均出现了转频、第1阶和第2阶油膜振荡频率的组合频率,而工况1只存在转频和第1阶油膜振荡频率的组合;除了复杂的频率结构外,第1阶和第2阶油膜振荡频率均在不同转速下存在能量之间的传递,即二者之间幅值相互影响.
(3)通过对两种数学模型在某些转速下的轴心轨迹和频谱图的比较,发现两种模型所反映的油膜振荡特性基本一致,但不同的模型对失稳转速的影响不同,相比而言有限元模型的失稳转速更低一些(可能与有限元法对系统的质量离散更为合理有关),但有限元模型所需的计算机资源和运算时间较多,如果精度要求不太高,集中质量法不失为较好的选择.

表2 质点5和节点24频率特征对比Tab.2 Frequency feature comparison of mass point 5and node 24
[1]ADILETTA G,GUIDO A R,ROSSI C.Chaotic motions of a rigid rotor in short journal bearings[J].Nonlinear Dynamics,1996,10(3):251-269.
[2]徐小峰,张文.一种非稳态油膜力模型下刚性转子的分岔和混沌特性[J].振动工程学报,2000,13(2):247-252.XU Xiaofeng,ZHANG Wen.Bifurcation and chaos of rigid unbalance rotor in short bearings under an unsteady oil-film force model[J].Journal of Vibration Engineering,2000,13(2):247-252.
[3]DE CASTRO H F,CAVALCA K L,NORDMANN R.Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model[J].Journal of Sound and Vibration,2008,317(1-2):273-293.
[4]李朝峰,戴继双,闻邦椿.膜支撑双盘转子-轴承系统周期运动稳定性与分岔[J].力学学报,2011,43(1):208-216.LI Chaofeng,DAI Jishuang,WEN Bangchun.Stability and bifurcation of the rotor-bearing system with double disks supported by cylindrical bearings[J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(1):208-216.
[5]李朝峰,孙伟,王得刚,等.两类转子-轴承系统模型非线性特性研究[J].中国机械工程,2009,20(2):218-221.LI Chaofeng,SUN Wei,WANG Degang,et al.Study on nonlinear characteristics of two type rotor-bearing systems[J].Chinese Journal of Mechanical Engineering,2009,20(2):218-221.
[6]张楠,吴乃军,刘占生,等.高速转子-轴承系统油膜涡动故障仿真研究[J].机械科学与技术,2011,30(1):48-51.ZHANG Nan,WU Naijun,LIU Zhansheng,et al.Fault mechanism of a rotor-bearing system with rubbing[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(1):48-51.
[7]DING Q,LEUNG A Y T.Numerical and experimental investigations on flexible multi-bearing rotor dynamics[J].Journal of Vibration and Acoustics,2005,127(4):408-415.
[8]杨金福,杨晟博,陈策,等.滑动轴承-转子系统的稳定性研究[J].航空动力学报,2008,23(8):1420-1426.YANG Jinfu,YANG Shengbo,CHEN Ce,et al.Research on sliding bearings and rotor system stability[J].Journal of Aerospace Power,2008,3(8):1420-1426.
[9]SCHWEIZERA B,SIEVERT M.Nonlinear oscillations of automotive turbocharger turbines[J].Journal of Sound and Vibration,2009,321(3-5):955–975.
[10]FAN C C,PAN M C.Active elimination of oil and dry whips in a rotating machine with an electromagnetic actuator[J].International Journal of Mechanical Sciences,2011,53(2):126-134.
[11]MUSZYNSKA A.Rotordynamics[M].New York:CRC Taylor & Francis Group,2005.
[12]EI-SHAFEI A,TAWFICK S H,RAAFAT M S,et al.Some experiments on oil whirl and oil whip[J].Journal of Engineering for Gas Turbines and Power,2007,129(1):144-153.
[13]JING J P,MENG G,SUN Y,et al.On the non-linear dynamic behavior of a rotor-bearing system[J].Journal of Sound and Vibration,2004,274(3-5):1031-1044.
[14]万召,孟光,荆建平,等.燃气轮机转子-轴承系统的油膜涡动分析[J].振动与冲击,2011,30(3):38-41.WAN Zhao,MENG Guang,JING Jianping,et al.Analysis on oil whirl of gas turbine rotor-bearing system [J].Journal of Vibration and Shock,2011,30(3):38-41.
[15]钟一谔,何衍宗,王正,等.转子动力学[M].北京:清华大学出版社,1987.ZHONG Yie,HE Yanzong,WANG Zheng,et al.Rotor dynamics[M].Beijing:Tsing hua University Press,1987.
[16]李朝峰.耦合故障复杂转子-轴承非线性系统的运行稳定性及其实验研究[D].沈阳:东北大学,2009.LI Chaofeng.Study on stability and experiments by complex rotor-bearing system with coupling faults[D].Shenyang:Northeastern University,2009.

