塔式起重机金属结构模态分析及其实验测试修正
王纲居,穆铭豪,孙远韬
(1.上海市建筑科学研究院,上海 200032;2.同济大学 机械与能源工程学院,上海 201804)
塔式起重机(以下简称塔机,见图1)是一种广泛应用于建筑施工的起重设备,主要由塔身、起重臂、塔帽和平衡臂组成,是典型的空间桁架结构.塔机在经常性的启、制动和进行复杂耦合运动时,塔机系统会产生强烈的冲击和振动,如产生大振幅的强迫振动且难以衰减,容易导致金属结构破坏,缩短使用寿命.为了避免塔机金属结构产生共振现象,同时使塔机结构的设计理论和方法更加合理,尽可能地提高结构的可靠性,所以有必要对塔机金属结构的动态特性进行研究,确保塔机在工作过程中满足强度条件和相关的动力性能要求.
本文通过有限元模型进行塔机动力学仿真,确定塔机的振动特性,获得了结构的固有频率和振型,可以对塔机受力特性作全面、详细的了解,分析影响其结构模态的主要因素,预测其结构在各种载荷与边界条件下的动态特性[1].在保证安全使用的前提下,获得较好的经济性.
1 结构模态分析的有限元法
在复杂结构的振动分析中,一般都需要建立结构的离散化力学模型,即把一个无穷多自由度的连续系统,通过离散化的方法,转变成为一个近似的多自由度系统来进行研究[2].塔机金属结构可以简化为由空间梁单元和杆单元组成的多自由度系统,系统的动力学方程为[3]

式中:[M]为系统的质量矩阵;[C]为系统的阻尼矩阵;[K]为系统的刚度矩阵;{x}为广义坐标;{Q}为广义力.
若忽略阻尼的作用,则系统的模态分析求解的是如式(2)所示的典型的广义特征值问题:
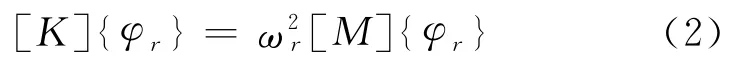
式中:ωr为第r阶模态的固有频率;{φr}为第r阶模态的振型向量.
机械结构的动态特性优劣可以用结构的模态参数(结构振动的各阶频率、阻尼及振型)判断.通过模态分析结果,可直观地显示塔机的动态特性和薄弱环节,为塔机的运行参数提供直接的理论分析依据.
2 有限元模型建立
某QTZ125型塔式起重机总高约57.9m(其中塔帽高7.6m),塔臂长约65.2m,平衡臂长13.4m,如图1a.塔身和起重臂臂杆件数目比较多,布置比较类似,基本都是由许多拓扑形状相同的杆件组成.
塔身、平衡臂弦杆和斜撑杆件均采用箱形截面三维beam189梁单元建模;水平塔臂、塔顶弦杆和斜撑杆件分别采用箱形和圆形截面三维梁单元建模;前后拉杆均采用矩形截面的杆单元建模.塔身、起重臂、塔帽和平衡臂的连接处结构比较复杂,关键部位的连接用变截面梁或假梁实现连接,如图1b、1c,次要部位的连接用节点直接布置在一起.配重箱、司机室等部件简化为质量点采用集中质量单元建模.
为了模拟实际约束情况把竖直塔身底部相应节点6个自由度全部约束.最后,塔机完整模型共有节点14 023个,单元7 352个.模态分析中,结构的固有频率和振型只与结构的质量分布、刚度分布和阻尼特性有关,和外载荷无关.
3 模态分析及结果
由振动理论可知,低阶固有频率对系统的动力响应贡献较大,而高阶固有频率影响较小,所以对塔机系统而言只要提取其低阶固有频率就能很好反映系统动力特性[4].
对塔机进行模态分析,计算了塔架金属结构7Hz以内的频率,1Hz以内的前5阶模态结果如表1所示.取固定工况下塔机的7Hz以内固有频率绘制成曲线,如图2所示.

图1 某型塔式起重机有限元模型Fig.1 Tower crane finite element model

表1 QTZ125塔机金属结构前5阶模态Tab.1 First 5th order modal of QTZ125tower crane
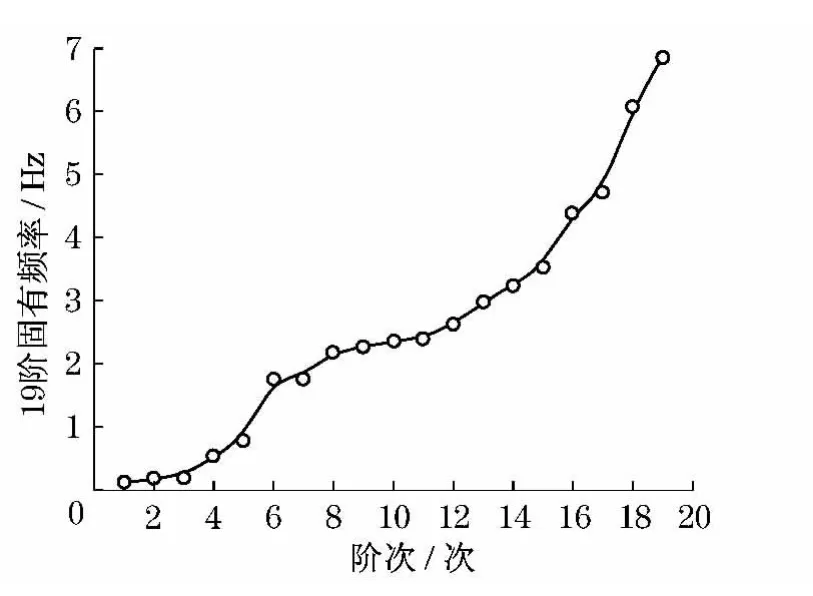
图2 固定工况下塔机7Hz以内固有频率Fig.2 Fixed condition natural frequency in 7Hz
根据固定工况下塔机的7Hz以内固有频率模态分析结果,塔机前5阶振动频率均较低,表明这类塔机整体振动频率偏低,虽然结构强度满足,但动刚度不足,抗变形能力弱,如需要可以通过扶墙适当加强其刚度,塔机1—6阶振型图3—8.
塔机第1、第5阶振型(见图3和图7)均是起重臂在回转平面的弯曲,说明了该型该平面内的刚度偏小,容易激发风载、重物倾斜等侧向载荷作用下侧向振动.
塔机第2—4阶振型(图4—6所示)均是塔身的模态,其中第1,2阶弯曲模态说明塔身的动刚度不足,承受风载等侧向载荷能力偏弱.
塔机第5阶振动频率为0.78Hz,而第6阶振动频率急剧变大为1.76Hz.第6阶振型是塔臂在回转平面内的3阶弯曲(图8).塔臂振型由2阶弯曲升为3阶弯曲,因此振动频率有了大幅提高.

图3 塔机第1阶振型(频率0.11Hz)Fig.3 1st order mode shape

图4 塔机第2阶振型(频率0.19Hz)Fig.4 2nd order mode shape

图5 塔机第3阶振型(频率0.21Hz)Fig.5 3rd order mode shape

图6 塔机第4阶振型(频率0.54Hz)Fig.6 4th order modal shape

图7 塔机第5阶振型(频率0.78Hz)Fig.7 5th order modal shape

图8 塔机第6阶振型(频率1.76Hz)Fig.8 6th order modal shape
4 实验验证
为了验证数值分析的准确性,在现场对该型塔机进行了模态测试.测试方案如图9和图10所示.测试仪器为东华DH5907A无线环境激励实验模态测试分析系统,传感器为磁电式速度传感器DH610,图11为现场测点传感器布置.
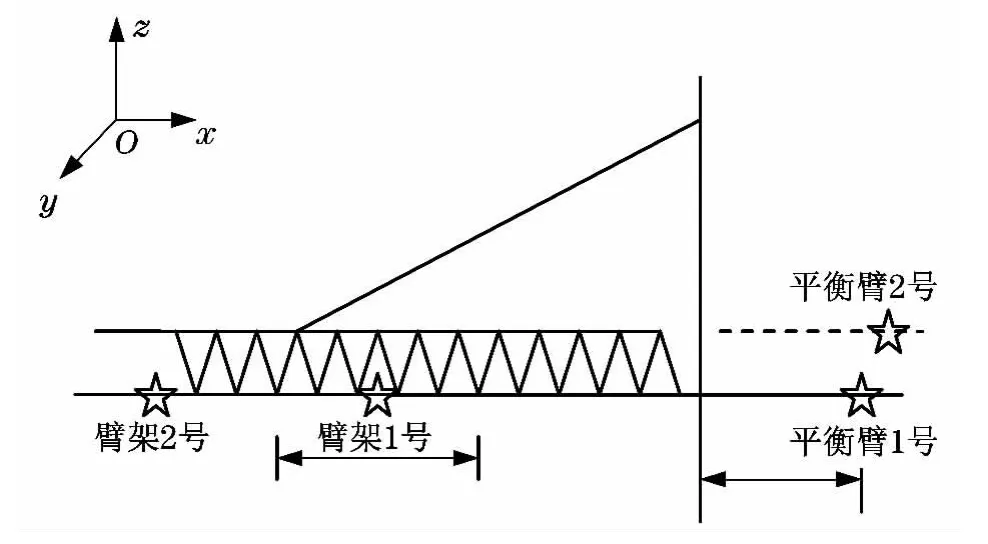
图9 仅测臂架振动传感器布置图Fig.9 Vibration sensor layout only for job
在塔机现场实测中,对风载荷作用下起重臂、平衡臂和塔身的速度响应进行了现场实测,记录了各测点的速度响应时间历程,响应时间历程的采样率100Hz,共进行6次竖向振动速度实验,图12是空载风振测试的竖向最大振动速度响应.
在实测风振响应的基础上,采用时域的随机子空间方法进行了塔机的试验模态参数识别,获得了塔机的低阶固有频率.

图11 现场振动传感器布置图Fig.11 Vibration sensor layout on site
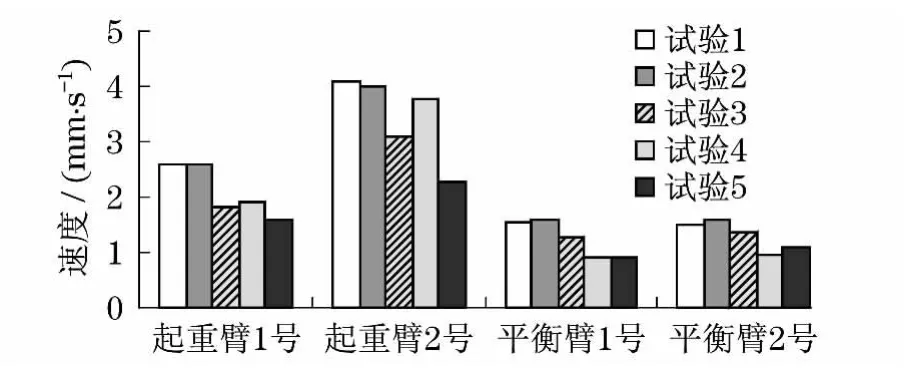
图12 空载风振测试的竖向最大振动速度响应Fig.12 Maximum vertical vibration velocity response of no-live load wind vibration test
与传统方法相比,随机子空间法有以下几点优点:一是该方法所需确定的参数少,只需确定模型的阶次;二是该方法无须迭代,也不涉及迭代的收敛性问题;三是模型缩减可直接从输入到输出数据中获得,无须计算1阶或高阶模型.
目前,随机子空间法有两种,一种是基于输出协方差的随机子空间法,另一种是基于数据的随机子空间法.
基于输出协方差的随机子空间法是将系统输出数据的协方差组合成Toeplitz矩阵,然后对Toeplitz矩阵进行奇异值分解(SVD),进而得到矩阵行列空间的信息——系统的可观性矩阵和可控性矩阵,利用系统可观性矩阵推移不变性质计算出系统的动态参数,进而识别出系统的模态参数.基于输出数据的随机子空间法是将系统的输出数据直接组合成Hankel矩阵,利用正交分解(QR分解)计算将来输出向过去输出上的投影,然后对投影进行奇异值分解,得到可观性矩阵和系统状态的卡尔曼滤波,由于环境激励与系统的状态无关,所以将卡尔曼滤波和输出代入到系统的状态空间方程,求解出结构的模态参数.
两种方法相比,第一种方法理论比较简单,但计算量比较大,第二种理论上比较难理解,但计算步骤清晰,计算量相对第一种较小.由于实验数据的输出向量较少,所以采用第一种方法——基于输出协方差的随机子空间法.

表2 试验机型的前5阶模态Tab.2 5orders modal of test machine
表3是试验机型的低阶固有频率的试验模态分析结果与有限元分析结果的对比,这表明,所建立的有限元模型的整体质量分布和刚度分布是准确的,试验振型的低阶固有振动性态(振型)有限元分析结果与试验结果一致.

表3 低阶固有频率试验值与分析值对比Tab.3 Test value comparison with analysis of value of the low order natural frequency
5 结论
本文对某QTZ125型塔式起重机的金属结构进行了模态分析,得到了结构的7Hz以内固有频率及振型.研究结果表明:该型塔机模态分析模型正确.整机的主要低阶频率偏低,动刚度不足,容易受低频载荷激扰而发生振动,需要引起后续设计及使用注意.
[1]沃德 海伦,斯蒂芬 拉门兹.模态分析理论与试验[M].白化同,郭继忠 译.北京:北京理工大学出版社,2001.WARD H,STEFAN L.Modal analysis theory and testing[M].BAI Huatong,GUO Jizhong translation.Beijing:Beijing Institute of Technology Press,2001.
[2]殷学钢,陈淮,蹇开林.结构振动分析的子结构方法[M].北京:中国铁道出版社,1991.YIN Xuegang,CHEN Huai,SAI Kailin.The substructure method of structure vibration analysis[M].Beijing:China Railway Publishing House,1991.
[3]CLOUGH R,PENZIEN J.Dynamics of structures.[M].New York:McGraw-Hill Education,2003:172-180.
[4]尹强,陈世教,冀满忠,基于ANSYS的塔式起重机结构模态分析[J].重庆建筑大学学报,2005,27(6):97-100.YIN Qiang,CHEN Shijiao,JI Manzhong.Modal analysis of tower crane structure based on ANSYS[J].Journal of Chongqing Architecture University,2005,27(6):97-100.

