基于带权重遗传算法的工程变幅机构优化设计
范 卿,曾 杨
(中联重科股份有限公司,湖南 长沙 410013)
变幅机构是工程机械赖以工作的核心元件,被广泛应用于车载吊、水泥输送泵、挖掘机等工程设备.对变幅机构的设计主要集中在绞点位置、连杆和变幅油缸,其目的是为了尽量减小机械工作过程中变幅油缸受到的压力[1].为此,文献[2]利用EXCEL表格实现了对三节点变幅机构的几何方程求解,当约束条件给定后,能迅速求解出铰点位置;文献[3]以三绞点模型分析了汽车起重机变幅机构的绞点位置优化设计方法,指出优化后的变幅机构能有效降低变幅过程中油路的压力冲击;文献[4]通过试凑法,分析了随车起重机在不同变幅机构下的受力情况,指出如果能进行优化设计,将能有效降低变幅机构的压力.
随着科技的发展,模糊算法[5]、神经网络算法[6]、遗传算法[7]和智能控制[8]等都在变幅结构的优化设计中得到了推广,但这些研究工作多将变幅机构等效为三节点模型,过于理想,同时也没有考虑优化目标的权重,使得结果收敛于局部.本文在分析了中联重科49m混凝土泵车的变幅机构后,采用带权重的遗传算法对其进行优化设计,获得了良好的效果.
1 变幅机构结构
变幅机构的结构如图1所示,由下节臂、上节臂、一号连杆、二号连杆和变幅油缸组成.为方便讨论,假定下节臂固定,即O,A点坐标在变幅过程中保持不变;初始情况下,油缸未动作,两节臂夹角α设定为0,即假定B,E的纵坐标相等.
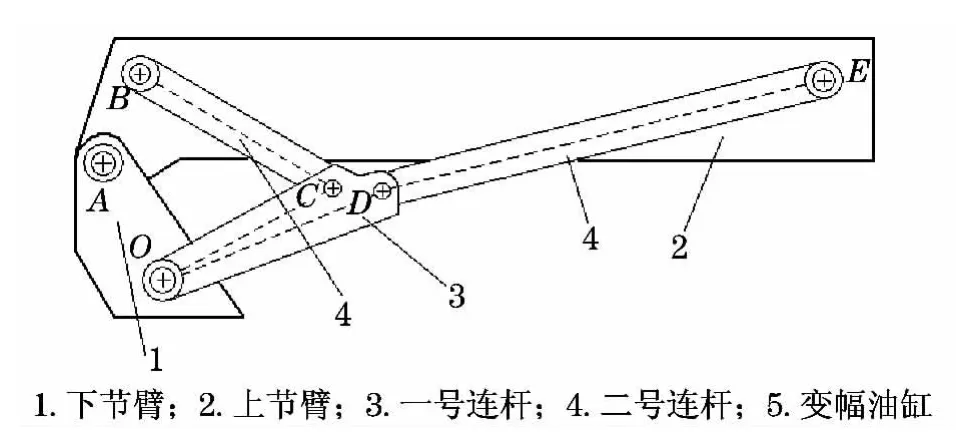
图1 变幅机构结构图Fig.1 Structure diagram of luffing system
其等效原理图如图2所示,设点A,B,C,D,E的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)、(x5,y5),并取油缸未动作时的B,E作为横坐标,则当上节臂在变幅油缸作用下上升α角度时,相当于EBA线段绕A点旋转α角,此时B点坐标变为
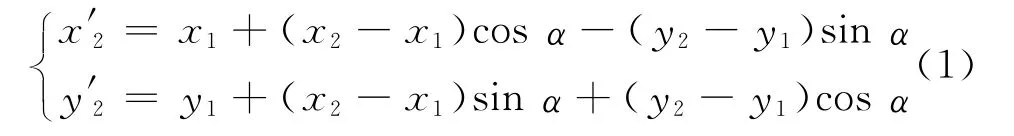
改写为矩阵形式:
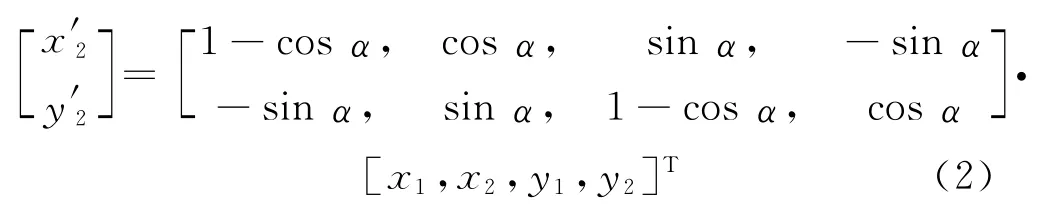
同理可求得其他各点的新坐标值,分别以(x′3,y′3),(x′4,y′4),(x′5,y′5)表示.
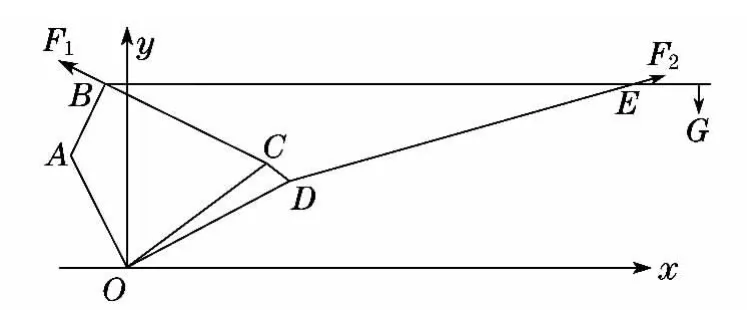
图2 变幅机构等效原理图Fig.2 Equivalent principle diagram of luffing system
依据变幅机构的工作特点知,A点和O点总力矩应分别平衡:
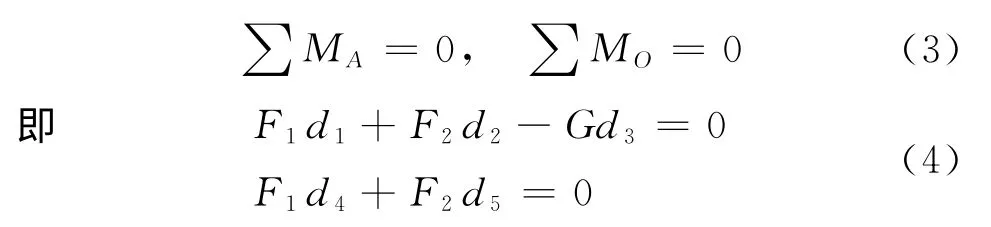
式中:F1,F2分别为二号连杆和油缸受到的压力;G为上节臂等效外部压力;d1—d5分别为相应的力臂,可以通过各点坐标求得.
由上分析可知,变幅油缸的压力F2是一个与O,A,B,C,D,E和α都相关的函数,可以表示为
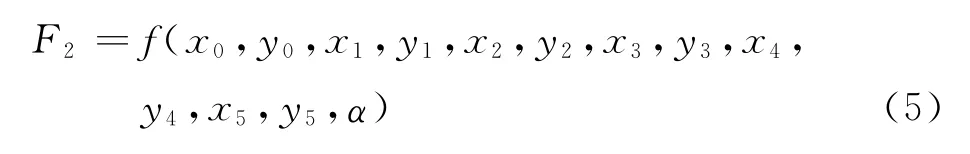
2 结构优化
对变幅结构的优化就是选择合适的坐标值,使得在相同的工况下,变幅油缸的受力最小;同时,当α变化时,油缸压力变化率也最小.为此,取优化目标函数为
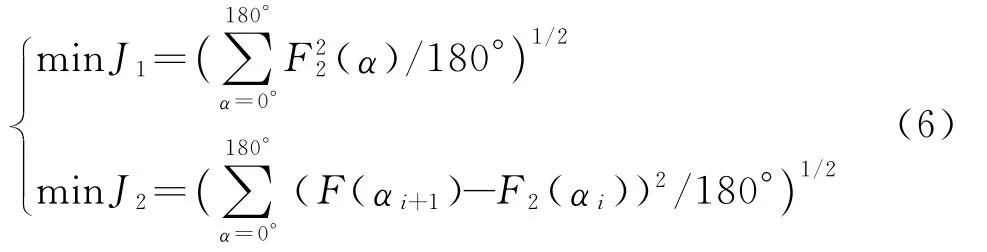
当一号臂没有起臂时,二号臂最大只能起臂90°.由于α是一个连续变化量,式(6)求解将会很复杂,工程中,可以只选择几个离散量进行计算.
综上所述,变幅机构的优化问题是一个典型的多目标优化问题.传统的遗传算法对优化目标直接构造适应度函数,没有考虑各个目标对变幅机构的影响程度是不一样的.为此,本文对适应度函数进行了修改.
以J1为例,设当J1>J1max时,变幅机构完全不能满足要求;当J1<J1min后,进一步减小J1值对变幅机构的影响很小,则可以构造如下适应度函数:
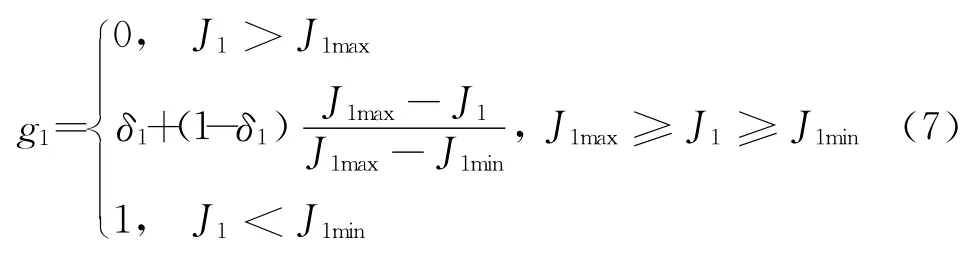
式中:0≤δ1≤1,为目标的重要程度.当J1max≥J1≥J1min时,δ1越大,该染色体被选中的概率越大.类似可以构造第二个目标的适应度函数g2.
在寻优过程中应使种群向g1较大的方向进化的同时,兼顾g2向较大的方向进化,使二者都能取得较好值,避免算法陷入局部最优解,具体寻优过程参加文献[9],这里不再赘述.
3 实例设计及仿真分析
式(5)含13个变量,为了简化计算,结合工程实际,在变幅机构未工作之前,即α=0°时,可以令A,B,G相对于O点的位置固定,C点相对于D点固定,E点纵坐标与B点纵坐标相等,并令O点位于坐标原点.在此基础上,当变幅机构起吊时,即α由0°到90°变化时,F2可表示为
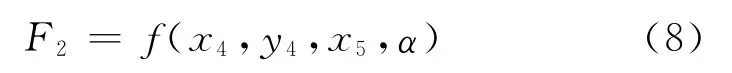
阈值J1max,J1min,J2max,J2min分别取油缸长期允许工作压力的90%,20%,30%,10%,δ1=0.5,δ2=0.2,α取0°,20°,40°,60°,80°共5个离散值进行计算;A,B,G点坐标分别为(-300mm,560 mm)、(-100mm,910mm)、(6 070mm,910mm);外部等效压力G=29 400N;C点坐标为(x4-230 mm,y4+120mm).采用优化算法后的坐标值与经验坐标值如表1所示.
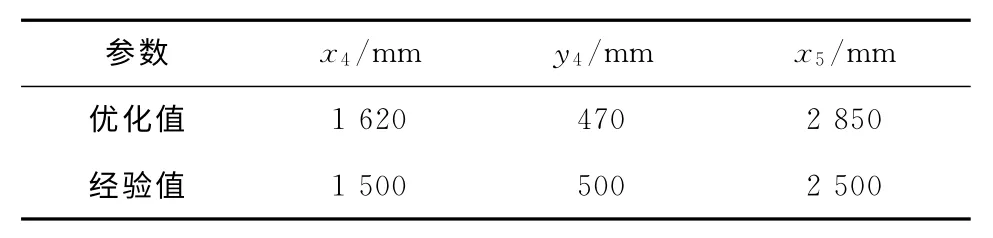
表1 优化坐标值Tab.1 Optimization coordinate value
利用优化参数,在MATLAB中进行了仿真分析,油缸压力曲线如图3所示.从图3中可以看出,相比于经验参数,采用优化参数后,油缸受到的最大压力得到了降低.同时,采用优化参数后,油缸受力曲线更加平坦,表示当α变化时,油缸所受冲击压力要小.

图3 优化前后油缸压力图Fig.3 Pressure diagram of oil cylinder
4 结论
工程变幅机构的优化设计能有效降低变幅油缸受到的压力,从而提高变幅机构的安全性和稳定性.本文在分析了中联重科49m混凝土泵车的变幅机构后,建立了其6节点模型,并采用带权重的遗传算法对变幅机构进行了优化设计,结果表明能有效降低变幅油缸的压力和压力变化率.需要指出的是,在优化设计过程中,假定变幅机构未动作(即未起吊)时A,B,C,G位置相对固定,这是为了简化计算,实质上,也可以将这4个点的坐标值一同进行优化,但势必增加计算量.
[1]陈苏秧,孙万勇.起重机变幅机构的改造[J].煤矿机械,2006,27(10):154-155.CHEN Suyang,SUN Wanyong.Transformation to organization of the hoist changing width[J].Coal Mine Machinery,2006,27(10):154-155.
[2]王华权.三角形变幅机构铰点求解器[J].建设机械技术与管理,2005,18(7):76-78.WANG Huaquan.Resolver of pivoting point for triangular luffer[J].Construction Machinery Technology & Management,2005,18(7):76-78.
[3]郑夕健,张璇,费桦.基于ADAMS的汽车起重机变幅机构优化设计[J].机械与电子,2008(7):3-5.ZHENG Xijian,ZHANG Xuan,FEI Hua.Optimization design of the amplitude variation mechanism of truck crane based on ADAMS[J].Machinery & Electronics,2008(7):3-5.
[4]魏效玲,张宁博,景晓桓.随车起重机变幅机构仿真与优化设计[J].河北建筑科技学院学报,2005,22(4):94-96.WEI Xiaoling,ZHANG Ningbo,JING Xiaohuan.Dynamic simulation and optimum design of luffing mechanism of lorry loading crane[J].Journal of Hebei Institute of Architectural Science & Technology,2005,22(4):94-96.
[5]席平原.塔式起重机变幅机构的模糊优化设计[J].起重运输机械,2005(7):12-14.XI Pingyuan.Fuzzy optimal design of luffing mechanism of tower crane[J].Hoisting and Conveying Machinery,2005(7):12-14.
[6]席平原,陈孟科,黄鹏.基于神经网络的塔机变幅机构遗传算法优化[J].起重运输机械,2007(3):24-25.XI Pingyuan,CHEN Mengke,HUANG Peng.Genetic algorithm optimization of tower crane luffing mechanism based on neural network[J].Hoisting and Conveying Machinery,2007(3):24-25.
[7]王启平,孙季华,谢能刚.基于遗传算法的四连杆变幅机构多目标模糊优化[J].安徽工业大学学报,2004,21(3):204-207.WANG Qiping,SUN Jihua,XIE Nenggang.Multi-objective fuzzy optimum design of four-bar l lufing mechanism of variation based on genetic algorithm[J].Journal of Anhui University of Technology,2004,21(3):204-207.
[8]陈天惠.塔机变幅机构的智能控制[J].建筑机械,2004(11):86-89.CHEN Tianhui.Intelligent control of tower crane luffing mechanism[J].Construction Machinery,2004(11):86-89.
[9]周明,孙树伟.遗传算法原理及应用[M].北京:国防科技图书出版社,1999.ZHOU Ming,SUN Shuwei.The principle and application of genetic algorithm[M].Beijing:National Defense Science and Technology Press,1999.

