动态(矿用)提升秤的校准方法探讨及测量不确定度的评定*
王 瑞
(甘肃省产品质量监督检验西部分中心,张掖 734000)
0 引言
动态(矿用)提升秤(行业中通常称为天轮式称重装置)是一种矿井口以提升形式使用的、对矿车或矿斗质量进行动态称量的衡器,用于政府监控垂直矿井矿产量的新型计量器具,目前尚无国家和地方校准规范,按照计量法律、法规的要求,必须对安装使用的动态(矿用)提升秤进行校准。本文介绍一种校准方法,并对该校准方法的测量不确定度进行了分析。
1 动态(矿用)提升秤的结构和工作原理
动态(矿用)提升秤由一套天轮式专用称重模块、控制柜、防雷部件等构成,安装在垂直升降的矿井口。其工作原理将称重传感器放在天轮的轴承座下方,当矿斗被垂直提升至矿井时,动态称量矿斗的重量,并将称量数据发至政府的监管部门。
2 校准方法
2.1 校准设备
1)校准用计量标准器具必须符合校准要求规定的M1等级砝码。
2)符合企业运输要求、质量稳定的矿斗,其装载物的性质和正常称量物一致或相似,可作为约定量值的标准矿斗。标准矿斗可用经过计量检定合格的衡器称出。
2.2 校准项目和校准方法
2.2.1 校准方法的选择
校准方法分为静态称量校准和动态称量校准。如果动态(矿用)提升秤具有静态功能时,才需要静态称量校准;如果动态(矿用)提升秤不具有静态功能,可以不进行静态称量校准。
2.2.2 静态称量校准
静态称量校准应当按照JJG 555—1996《非自动衡器通用检定规程》要求进行静态称量校准,包括置零准确度、去皮准确度、偏载、称量以及重复性的校准。
2.2.3 动态称量校准
1)参考矿斗及校准载荷的选择
校准使用的参考矿斗应选取代表性的矿斗,应当选择磨损轻,各部件完整的矿斗作为参考矿斗。参考矿斗所代表的校准载荷应覆盖动态(矿用)提升秤的称量范围,即空载至最大秤量,如果实际使用的载荷达不到最大秤量,可以采用常用秤量。
具体选择校准载荷时,选取空载、1/2最大秤量、最大秤量,主要考察动态(矿用)提升秤的整个称量范围的准确性。
2)参考矿斗质量的约定量值
参考矿斗质量的约定量值,通过对矿斗称量可得到,在检定合格的称量衡器上予以确定。称量时应保证矿斗处于静止状态,并全部置于衡器上,对参考矿斗称量3次,取3次称量结果的算术平均值作为矿斗质量的约定量值。
采用标准砝码作为载荷,可以按照上述方法确定参考矿斗质量的约定量值,再与所加的标准砝码质量相加即为参考矿斗质量的约定量值。
3)动态称量误差校准
按照上面确定的矿斗进行动态称量误差校准,对矿斗的每种载荷均进行10次动态称量,且速度每次都匀速相等,记录动态校准时参考矿斗质量,并按照式(1)计算动态(矿用)提升秤称量误差Ei:
(1)
式中:i为承载器容器动态称量的次数,i=1,2,3,…,n,n=10;Mdi为承载器容器第i次动态称量质量示值;Mref为承载器容器的约定真值。
3 动态(矿用)提升秤测量结果不确定度评定
用于M1等级标准砝码校准动态(矿用)提升秤称量结果的不确定度评定,采取直接比较法,用砝码直接加载、卸载的方式,分段称量示值与标准砝码之差即为提升秤的示值误差。
3.1 数学模型
ΔM=M-M0
式中:ΔM为提升秤称量误差;M为提升秤的示值;M0为砝码的质量。
灵敏系数:
c1=∂ΔM/∂M=1c2=∂ΔM/∂M0=-1
3.2 不确定度来源及评定
3.2.1 不确定度来源
标准装置在测量提升秤时的不确定度来源见表1。
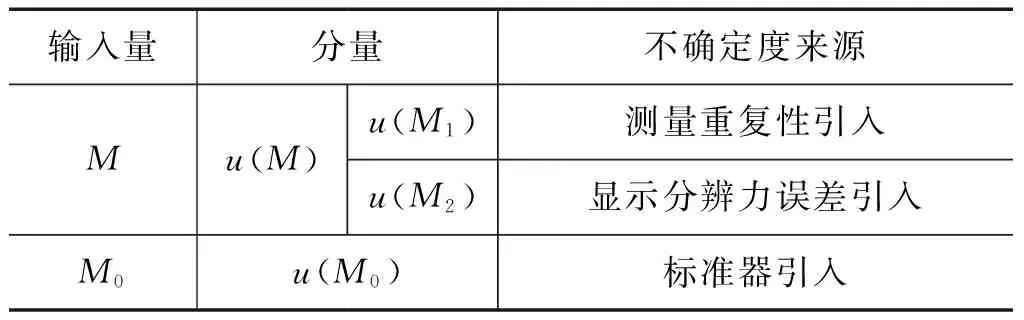
表1标准装置在测量提升秤时的不确定度来源
3.2.2 评定各输入量的标准不确定度
1)计算重复测量引入的不确定度分量u(M1)
选一台具有约定量值的砝码矿斗作为被测对象,速度为≤5km/h,且匀速。在1000kg点重复测量10次,得到10个观测值(被测显示读数和砝码矿斗标准值之间的差值):10,-20,0,10,0,0,-30,0,0,10 kg。10次测量结果的平均值为998kg,最大示值误差为-30kg。得到标准偏差:
以10次测量的平均值作为测量结果,所以:
2)计算显示分辨力引入的不确定度分量u(M2)
数字示值的分度值为d=10kg,显示分辨力为1d,无法采用“闪变点法”,故由被测提升秤数字示值分辨力引入的测量不确定度分量:
3)标准器M0引入的不确定度分量u(M0)
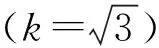
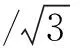
所使用称量衡器在500kg,最大允许误差为|MPE|=0.5kg,其标准不确定度:
3.3 合成标准不确定度uc(y)
1)扩展不确定度
取包含因子:k=2,U=kuc(y)=2×5=10kg,相对扩展不确定度Ur=1%
2)动态称量校准结果
动态(矿用)提升秤最大示值误差为-3.0%,相对扩展不确定度Ur=1%,k=2。
3.4 测量不确定度报告与表示
Ur=1%,k=2
4 结束语
通过对多家企业使用的动态(矿用)提升秤进行校准,经使用单位验证,结果表明:校准方法科学合理、切实可行。
[1] JJG 555—1996非自动秤通用检定规程[S].北京:中国计量出版社,1997
[2] JJF 1001—2011通用计量术语及定义技术规范[S].北京:中国质检出版社,2012
[3] JJF 1059—1999 测量不确定度评定与表示[S].北京:中国计量出版社,1999
[4] 倪育才.实用测量不确定度评定[M].北京:中国计量出版社,2008
[5] 李庆忠,李宇红.计量不确定度评估要点[J].计量技术.2003(1)

