碳纳米管电导率的介质谐振器法测量研究*
赵 飞 沙长涛 王 珂
(工业和信息化部电子工业标准化研究院计量与检测中心,北京 100176)
0 引言
介质柱谐振器是指一根圆柱形介质柱,其两端面被无限大的平行导电板短路而构成的谐振系统。介质谐振器法最初是由B.W.Hakki和P.D.Coleman[1]提出的,因此又叫Hakki-Coleman法,后来,介质谐振器法经过W.E.Courtney[2]的进一步改进后成为最常用的微波介电性能测量方法,现已广泛应用于高介、低损耗材料的微波介电性能的测量。
在需要使用纳米管或纳米线的电子器件中,其工作频率往往处于微波至毫米波频带,因此,针对纳米管的电性能测量就变得非常重要。纳米管的电导率的理论模型目前普遍采用Luttinger模型[3]。近些年来,人们使用了许多方法从理论上和实验角度对碳纳米管的电导率进行了研究[4]。有人试图将单根碳纳米管焊接到沉积在传输线上的微导体上,再通过电路模型来估算出其电导率[3,5]。然而,这些方法都存在明显的问题,即纳米管与传输线之间存在很大的阻抗不匹配,以及焊接处存在未知的接触电阻。本文中所采用的方法不存在上述问题,通过该方法获得的电导率是一个对许多纳米管测量所得到的有效平均值。
本文将首先建立利用介质谐振器法测量碳纳米管电导率的理论模型,然后介绍了校准方法和测量细节,并对其不确定度进行了分析。
1 实验方法
被测碳纳米管样品从Aldrich公司购得。将碳纳米管分散在氯仿中,碳纳米管与氯仿的质量比约为1:100。将混合液超声分散10分钟后再以约7kPa的压力喷涂到介质柱的一个或两个端面上,这里需要注意,喷涂厚度应该大于几个电趋肤深度,趋肤深度δs可以用如下公式计算:
(1)
式中,fr为谐振频率;μ0分别真空磁导率;σ为端面的电导率。从式(1)可以看出,如果假设不同频率下的电导率基本不变,谐振频率(即测试频率)越低,趋肤深度越大,也就是说样品制备时喷涂厚度要厚一些。
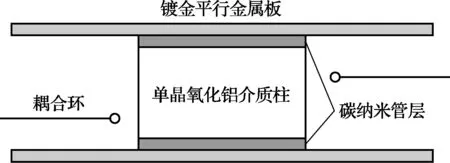
图1 测量时两端面喷涂碳纳米管的介质柱放置在平行金属板之间的示意图
在本文所采用的测量方法中,被测碳纳米管要预先喷涂在具有高品质因数的石英介质圆柱的两个端面上,再将介质圆柱置于两金属平行板之间,构成介质谐振器(如图1),通过测量介质圆柱端面喷涂碳纳米管前后的介质谐振器的谐振频率和品质因数的变化来计算碳纳米管层的表面电阻及电导率。介质柱的介电常数需要通过测量谐振频率而计算得到,并用于计算喷涂碳纳米管的谐振器端面的电导率。该方法可以实现的测量频率范围广,通过选择不同尺寸的介质柱,可以实现微波到毫米波的测量。该方法较之其他传输线法的另一优点是可以将装置的金属损耗影响降至最小。
2 理论模型
本文中介绍的介质谐振器法基于电磁场模型计算电导率,该电磁场模型使用喷涂碳纳米管前后的介质谐振器的谐振频率fr和品质因数Q的变化来计算碳纳米管层的等效电导率。通过穿过谐振器-纳米管界面的电场和磁场的切向分量可以得到关于谐振频率的超越方程[6]:
(2)
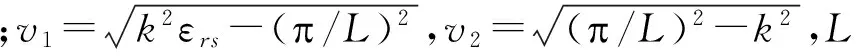
(3)
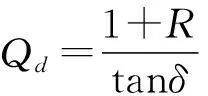
(4)
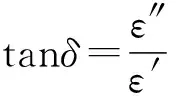
(5)
(6)
根据式(3)~式(6),可以得到表面电阻Rs:
(7)
式中,εr为涂覆碳纳米管后介质圆柱的相对介电常数;l为谐振频率fr对应的微波波长。在得到表面电阻Rs之后,再根据已知的被测碳纳米管为非磁性的这一条件,就可以根据以下公式计算出其电导率:
(8)
3 测量结果与讨论
在进行利用网络分析仪对所需要的S21参数进行测量采集之前,需要对其进行校准,方法是利用一根长度等于两根耦合同轴线长度之和的同轴线与两端口电缆相连,进行通路校准,校准后的S21参数在通过同轴线直通时显示为0.1 dB左右。
为了测量不同频率下的电导率,实验中分别选择了三种不同尺寸的单晶氧化铝圆柱作为构成介质谐振器的介质,其尺寸和TE011谐振频率如表1所示,可见,如果需要进行更高频率的测量值,则需要更小尺寸的介质圆柱,当所准备的介质谐振器尺寸足够小时,其谐振频率甚至可以达到毫米波范围,从而可能实现毫米波频率下的碳纳米管的电导率测量。
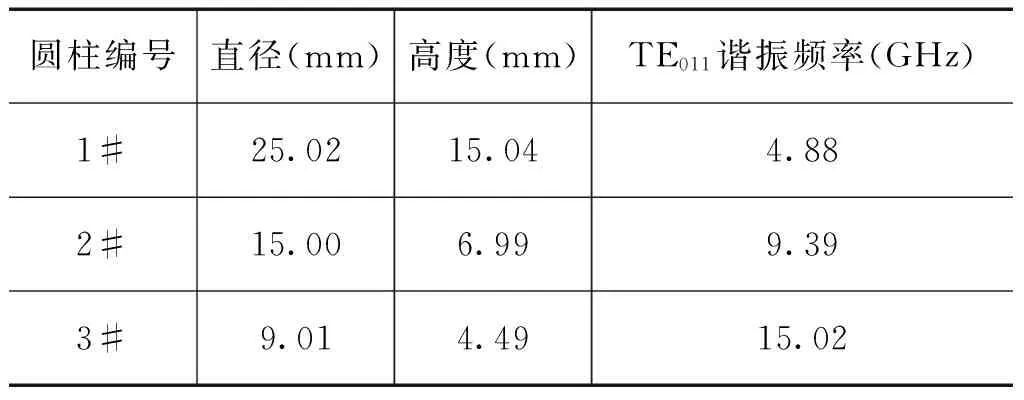
表1不同尺寸的单晶氧化铝圆柱及对应的TE011谐振频率

图2 平行板介质谐振器法测量夹具实物图
本实验中所喷涂的碳纳米管厚度大约为30~50μm。测试时将喷涂碳纳米管前后的单晶氧化铝圆柱先后放置在如图2所示的平行板测试夹具中。一对耦合环激励出TE011谐振模。先后分别测量喷涂碳纳米管前后的介质谐振器的TE011谐振模的品质因数Q和谐振频率fr。最后,可以根据式(7)和式(8)分别计算出碳纳米管的表面电阻和有效电导率。
每种尺寸的介质柱各制备两个样品,分别测量其有效电导率,结果见表2。另外,为了进一步验证本方法的测量效果,对同一个样品在不同时间分别进行多次测量,所得结果见表3。
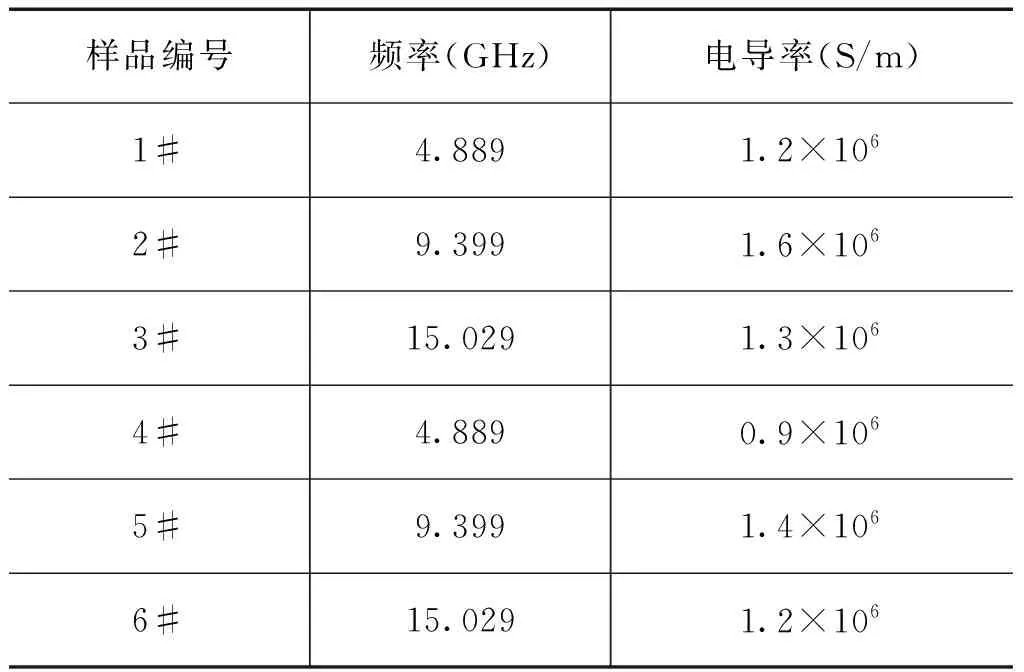
表2喷涂在三种不同尺寸的介质圆柱端面的碳纳米管的有效电导率
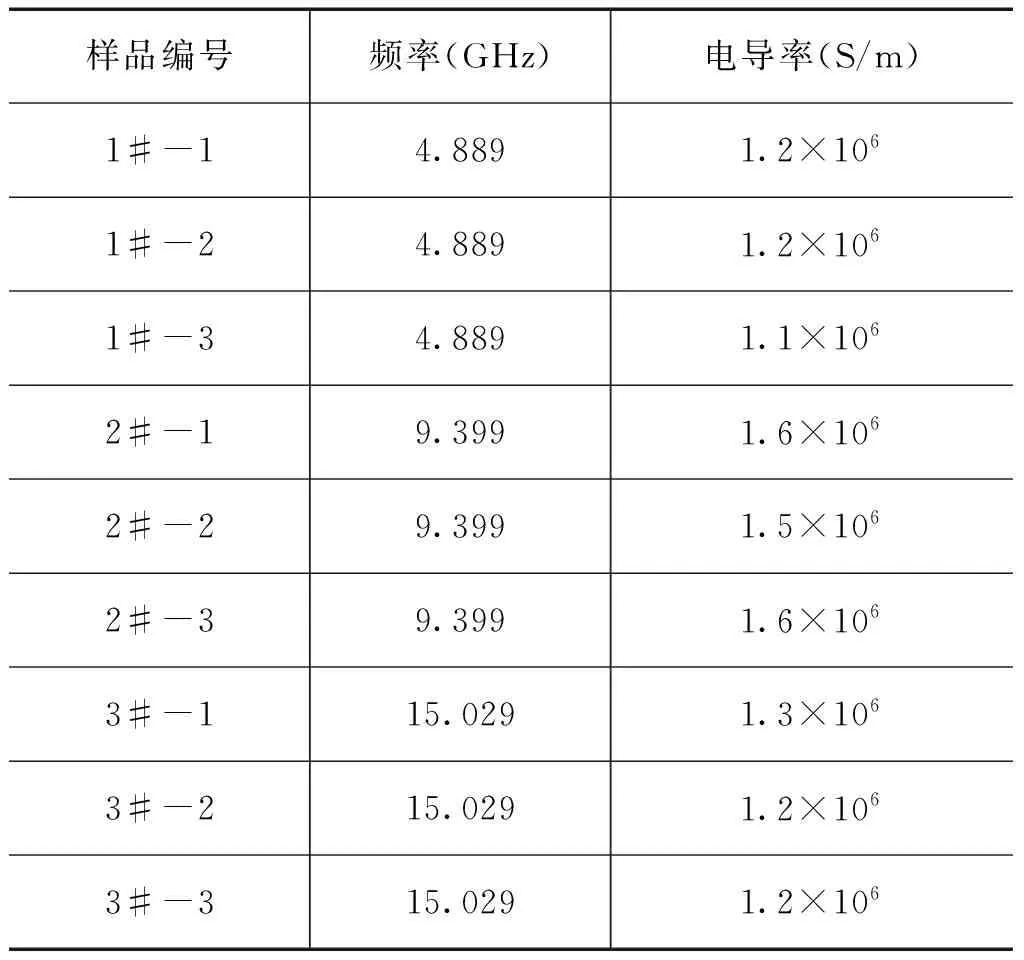
表3同一样品的电导率重复性测量结果
从表2可以看出,对于不同的样品,测得的碳纳米管的电导率数值上相差很大,这主要是因为喷涂沉积过程及沉积的碳纳米管可能存在较大差异等原因造成的。另一方面,从表3中可以看出,对于同一个样品,其测量结果一致性则非常好。
基于前一部分的计算模型分析,可以得出与电导率的测量不确定性有关的因素有:介质圆柱的尺寸、碳纳米管涂层的厚度、Q值和谐振频率fr,其中,最主要的因素是涂层厚度和Q值。通过对本测量装置测量结果不确定度分析,以及对其进行重复性、稳定性实验,归纳出的电导率不确定度约为3×105。
4 结束语
本文介绍了介质谐振器法测量碳纳米管微波电导率的装置组成,阐述了该测量方法的基本原理和计算模型,给出了利用该方法得到的一系列测量结果,并对其不确定度进行了分析。该技术可以降低接触电阻和阻抗不匹配对测量的影响,同时也使夹具与金属之间损耗实现了最小化。利用介质谐振器法可以实现对纳米管和纳米线在微波至毫米波频段的电导率特性的测量。
[1] B.W.Hakki and P.D.Coleman:A dielectric resonator method of measuring inductive in the millimeter range,IRE Transactions on Microwave Theory Technology,MMT-8,P 402-410,1960
[2] W.E.Courtney:Analysis and evaluation of a method of measuring the complex permittivity and permeability of microwave insulators,IEEE Transactions on Microwave Theory and Techniques,18,P 476-485,1970
[3] P.J.Burke:Luttinger liquid theory as a model of the gigahertz electrical properties of carbon nanotubes,IEEE Transactions on Nanotechnology,1,P 129-144,2002
[4] P.Singjai,S.Changsarn and S.Thongtem:Electrical resistivity of bulk multi-walled carbon nanotubes synthesized by an infusion chemical vapor deposition method,Materials Scienece and Engineering A,443,P 42-46,2007
[5] P.Chiu and I.Shih:A study of the size effect on the temperature-dependent resistivity of bismuth nanowires with rectangular cross-sections,Nanotechnology,15,P 1489-1492,2004
[6] Z.Y.Shen,C.Wilker,P.Pang,et al.:High Tcsuperconductor-sapphire microwave resonator with extremely high Q-values up to 90 K,IEEE Transactions on Microwave Theory and Techniques,40,P 2424-2431,1992

