自准直经纬仪测角系统及不确定度分析*

黄仙锦 卜雄洙 杨 波 向 超

(南京理工大学 机械工程学院仪器科学与技术系，南京市 210094)

0 引言

随着现代工业的快速发展，大型设备精密制造和安装对测量工作提出了很高的要求[1-2]。特别是在船舶制造、重型机械制造等部门，常采用镜面法线来提供高精度的方向基准[3]。自准直经纬仪[4]因其测量精度高、操作简单及可靠性好等特点在高精度安装和方向基准建立中得到广泛应用，如利用自准直经纬仪进行艏艉线标校及测量和新装设备的艇体坐标系引建[5]等。但是在一些特殊安装条件下，安装面与水平面存在倾角时，参考反射镜置于安装面上，自准直经纬仪无法直接瞄准参考反射镜，必须通过中间反射镜对角度进行测量。针对以上问题，需建立相应空间理论模型对该角度测量方法的原理进行分析，并进行实验验证。

1 测量原理及系统组成

1.1 测量原理

角度测量原理如图1所示。测量时，调平中间平面反射镜，自准直经纬仪发出十字光线，经中间平面反射镜反射到待测参考反射镜上，调节自准直经纬仪，使十字光线垂直的照射到待测参考反射镜上，光路原路返回，在自准直经纬仪的目镜分划板上形成十字成像，微调使其中心与目镜上刻度线中心重合。此时读取经纬仪上垂直角示值，即图1中的角l′，根据光路可知l1=l′，便可测得待测参考反射镜与水平面的夹角。

图1 角度测量原理图

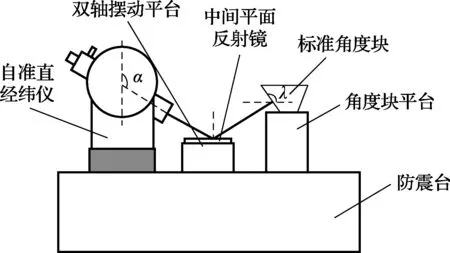
图2 垂直角测量系统组成

1.2 测量系统组成

垂直角测量系统组成如图2所示。测量系统由自准直经纬仪、中间平面反射镜、双轴摆动平台(包括控制器)、标准角度块等组成。所设计标准角度块反射面与水平面夹角为l，该值与图1中所示安装角度l1相对应。中间平面反射镜置于双轴摆动平台上，参考水平由高精度电子水平仪提供，高精度电子水平仪的自校准和双轴摆动平台的自动调平控制由计算机软件实现。

2 角度测量解算方法

2.1 角度解算模型建立

测量光路示意图如图3所示。实际测量中，中间反射镜是不能达到完全水平的，需利用坐标转换的解算原理来分析中间反射镜垂直和水平两个方向转角对待测参考反射镜角度测量的影响。

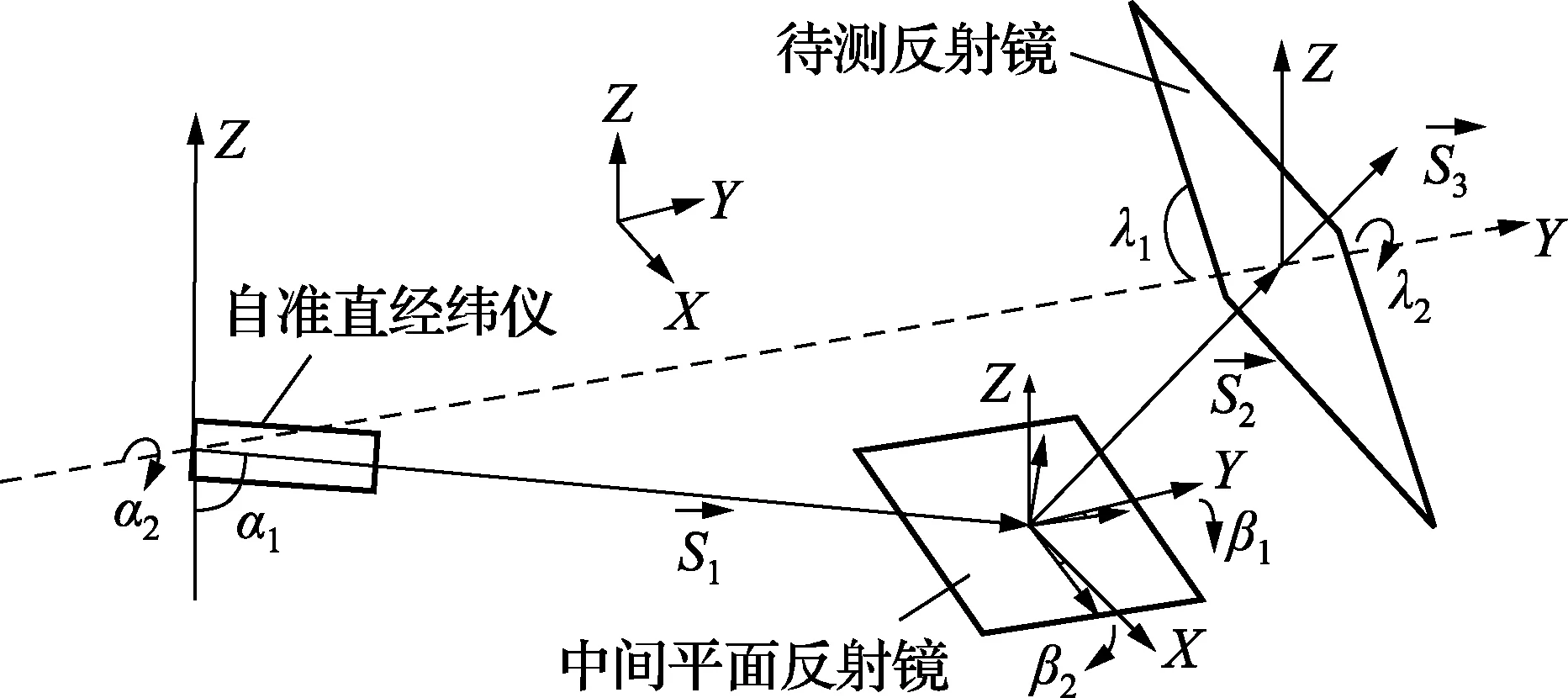
图3 角度解算光路示意图

2.2 角度解算模型求解

当不考虑水平方向的转角时，即a2、β2、l2等于0，有如下结果

当不考虑中间反射镜的转角，即β1=0,β2=0时，有如下结果

当a1、a2、β1、β2都考虑时，有如下结果

sinl1cosl2=2cosa2sina1cos2β1cos2β2

-cosa1cosa2sin2β1cos2β2

-2cosa2sina1cos2β2

+sina2sinβ1sin2β2+cosa2sina1

(1)

cosl1cosl2=2cosa1cosa2cos2β1cos2β2

+cosa2sina1sin2β1cos2β2

-sina2sin2β2cosβ1-cosa1cosa2

(2)

当两个方向都有转角时，在计算过程中会互相产生影响。因β1、β2极限值为3.60″，其值非常小，则可将sinβ1sinβ2≈0、sin2β1≈0、sin2β2≈0，利用上述关系分别对式(1)、(2)进行化简得

sinl1cosl2=cosa2sin(a1-2β1)

(3)

cosl1cosl2=cosa2cos(a1-2β1)-sina2sin2β2

(4)

将式(4)除式(3)得

(5)

在极限情况下a2=32″、β2=3.6″，得tana2sin2β2=5.0×10-9，且式(5)第二项中分母为非零项，故该项对测量结果近似为零，解得角度测量的数学模型为

l1=a1-2β1

(6)

因此，当转角a2、β2值在一定范围内时的角度解算结果与a2、β2、l2等于0的解算结果完全一致。故在一定的安装角范围内，式(6)将作为角度测量的数学模型。

2.3 角度解算验证

实验结果如表1所示，给出了实际测量结果和利用解算公式(1)、(2)解算出的结果。

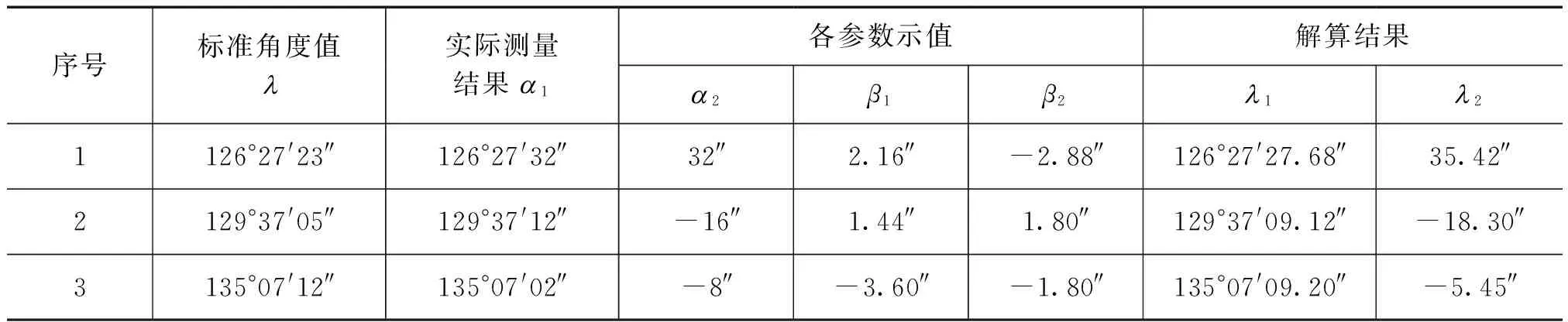
表1实验结果记录

引入角度解算算法后的结果见l1、l2。对比后可知，引入角度解算算法后的结果与角度测量的数学模型式(6)相一致，从而验证了角度解算的正确性，修正了中间反射镜存在安装角度时所带来的测量误差。

3 不确定度评定

3.1 数学模型

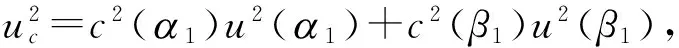
3.2 不确定度分量评定

3.2.1 与自准直经纬仪读数有关的标准不确定度分量u(a1)

1)自准直经纬仪量化误差引入的标准不确定度分量u1

2)自准直经纬仪瞄准引入的标准不确定度分量u2

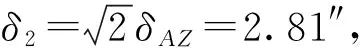
3)中间反射镜平面度误差引入的标准不确定度分量u3

4)测量平均值标准差引入的标准不确定分量u4

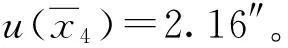
由以上各分量得到与自准直经纬仪有关的标准不确定度分量

3.2.2 高精度电子水平仪引入的标准不确定度分量u(β1)

3.3 合成标准不确定度

3.4 扩展不确定度

取置信水准ρ=0.95，t95(28)=2.048，则测量系统的扩展不确定度U95=2.048uc=5.90″。

4 结论

本文设计的利用光电自准直经纬仪通过中间反射镜测量安装反射镜垂直角的测量系统可以对受结构及安装条件限制下的反射镜垂直角进行测量，所建立的角度测量数学模型可修正中间反射镜存在安装角度误差时的测量结果。通过实验最终得到的结果与理论分析相吻合，该系统扩展不确定度为5.90″，满足设计要求，具有一定的工程应用价值。

[1] 窦艳红，马钟焕，等.一种汽车部件角度参数测量方法的探讨[J].计量学报，2010,31(6A):191-193

[2] 杨振，李广云，等.光学准直测量方法与精度分析[J].红外与激光工程，2011,40(2):282-286

[3] 陈继华，黄剑波，等.一种新的经纬仪自准直方法[J].测绘科学技术学报，2006,23(5):338-344

[4] 周红锋，宫爱玲.小角度测量的光学方法[J].计量技术，2006,(17):17-19

[5] 王悦勇，郭喜庆，等.—种舰艇艏艉线方位基准的静态标校方法与误差分析[J].测试技术学报，2002,16:867-872

[6] 张辉.小角度检查仪复现标准角度的不确定度评定[J].计量技术2003,(11):54-56

[7] 费业泰.误差理论与数据处理[M].北京:机械工业出版社，2000:82-92

[8] 马骊群，王继虎，等.激光跟踪仪测角误差的位移标定法[J].计量学报，2009,30(5A):76-78

[9] 张宁，林家明，等.光学角规偏向角的测量方法及不确定度分析和应用的探讨[J].计量学报，2006,27(3A):85-87

[10] J E Muelaner，Z Wang，et al.Study of the Uncertainty of Angle Measurement for a Rotary-laser Automatic Theodolite[J].Journal of Engineering Manufacture，2009，223(3):217-229

[11] Zhao Lirong，Zhu Wei，et al.The Method of the System Error Modification of Photoelectric Theodolite of T Type[J].International Conference on Optoelectronics and Microelectronics，2012:384-387