基于MATLAB的应力环校准方程线性回归分析*

朱 林 李志峰 何建新 毛勤卫

(常州计量测试技术研究所，常州 213001)

0 引言

硫化物应力腐蚀开裂(SSC)是金属材料在硫化物腐蚀环境中受一定的应力作用产生的开裂形式，由于其导致的破坏往往是没有明显预兆的脆性断裂，因而危害性很大。工程实践中硫化物应力腐蚀开裂试验的常用载荷测量方法是通过测量应力环的变形量来计算载荷，在试验中当应力环的量程范围选择合适时，应力环产生的载荷与变形量有近似线性的关系[1]。

目前，我所检测的该类应力环多为进口产品，送检客户要求提供类似国外的出厂检验报告，这就需要对应力环进行线性回归分析，给出其校准方程。此校准方程即为负载关于百分表变形量的曲线拟合方程。所谓曲线拟合就是拟合测量数据曲线，有时所选择的曲线通过数据点，但在其他点上，曲线接近它们而不必通过它们。

1 应力环的测量数据及最小二乘法的线性回归分析

1.1 应力环的测量数据

按照JJG 144—2007《标准测力仪》要求，用力标准机和百分表对美国Cortest公司生产的34kN应力环进行测量校准，所获数据见表1。

表1应力环测量数据

应力环荷载量与百分表行程具有线性关系，假设测量数据有如下结构形式：

(1)

式中：yt为百分表的变形量；xt为载荷值，β0，…，β3为3次多项式拟合曲线的系数；εi表示其他因素对变形量的影响的总和，一般假设它们是一组相互独立，并服从同一正态分布N(0,σ)的随机变量。

在应力环测量过程中，将负载看作一般变量而不作为随机变量，因而忽略εi的影响。曲线拟合问题主要就是求解出多项式曲线的系数问题[2]。

1.2 最小二乘法线性回归分析

通常大多数试验室采用平均值法作为简便的回归分析方法。该方法因简单、便于理解而深受试验人员青睐，但是又因其精度较低、对试验数据的线性要求很高等缺点使得回归分析结果的准确性大受影响。且国外应力环的出厂检验报告曲线拟合方程为三次多项式方程，因此用平均值法已经无法满足要求，而最小二乘法不仅能满足多项式拟合要求，且回归分析精度高、可信赖，因此是应力环线性回归分析方法的最佳选择。

所谓最小二乘曲线拟合，就是使误差平方和最小的多项式拟合，即寻找一条曲线使在误差平方和最小的准则下与所有数据点最为接近。为提高曲线拟合的精度，与输入输出的多项式的次数有关，根据国外出厂提供的检验报告和我所对该应力环检验校准经验所得，一般取到输入的三次项即可，根据式(1)负载与变形量的校准方程有如下的三项式关系：

yt=β0xt3+β1xt2+β2xt+β3

(2)

如果检定点为n个，根据方程(2)则可列出其误差方程为：

(3)

上述误差方程组(3)用矩阵表示为：

V=Y-PA

(4)

同样，由残差平方和最小这一条件，可得矩阵形式正规方程：

PTV=0

并得矩阵形式的解为：

A=(PTP)-1PTY

(5)

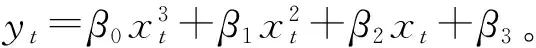
2 用MATLAB实现校准方程的曲线拟合

MATLAB 是一个高级的数值分析处理与计算软件，求解矩阵方程非常方便。运用MATLAB软件处理最小二乘法的曲线拟合问题，既可以直接用最小二乘法的计算原理编程处理，也可以用MATLAB提供的Polyfit函数来计算多项式拟合系数，函数Polyfit的输入量为x、y、n，其中x、y即为需要建立相互关系的两个量的测量值，以数组的形式输入n为多项式的次数，输出的是多项式系数的行向量，而得到的多项式是降幂的。以下介绍用Polyfit函数来解决应力环校准方程的曲线拟合问题。

[命令]

polyfit

[调用格式]

p3=polyfit(x,y,n)

[功能]

对于已知的数据组x，y进行多项式拟合，拟合的多项式的阶数为n，其中p3为3次多项式的系数矩阵。

在MATLAB的命令窗口输入如下的程序代码：

x=[0,5,9,13,17,21,25,30,34];

y=[0.000,0.514,0.910,1.308,1.702,2.103,2.507,3.015,3.429];

p3=polyfit(x,y,3);

p=polyval(p3,x);

hold on;

p3=

5.3723e-006-2.3676e-004 1.0267e-001 1.8190e-003，即得到应力环校准方程为：

(1.02676e-001)xt+1.8190e-003

其拟合曲线图形如图1所示。

在图1中，小圆点表示测量应力环原始数据中载荷值与百分表变形量所对应的点，斜线为拟合后的曲线，从图中可以看出运用MATLAB拟合出负载关于变形量的曲线效果非常好[4-5]，完全满足了客户对于进口应力环检测校准的要求。

图1 拟合曲线图形

3 结语

在MATLAB环境下解决应力环校准方程的曲线拟合问题，不仅满足了客户对应力环校准检验报告的要求，同时也为计量人员对应力环的检验数据的处理提供了一种快捷有效的办法，此方法值得在计量校准工作过程中推广应用。

[1] 黄仲婴，袁鹏斌，陶廷记，等. 硫化物应力腐蚀开裂试验应力环载荷的测量及标定[J].理化检验-物理分册，2010，46(3):183-185

[2] 麻青春，钱武威. 基于最小二乘法的测力环线性回归分析与检验[J].交通标准化，2009，202(15):137-139

[3] 杜水友，章皓，郑永军，等. 最小二乘法拟合压力传感器二次曲线及精度分析[J]. 中国计量学院学报，2005(16):185-187

[4] 吕喜明，李明远. 最小二乘曲线拟合的MATLAB实现[J]. 内蒙古民族大学学报(自然科学版)，2009，24 (2):125-127

[5] 罗永会，要秉文，姚少巍. Matlab稳健回归在建立校准曲线中的应用[J].计量技术，2008(1):54-55