整流器内部流场的数值模拟研究*

王菊芬

(空军油料研究所，北京 100076)

0 引言

通常，流量计的标定都是在充分发展流态下进行的。然而测量环境中各种管线配件产生的流体干扰，如漩涡流、扁平流和非对称流，严重影响流量计的测量精度。由于安装空间受限，往往难以提供足够长的直管段以形成充分发展流，而加装整流器是一个有效的解决办法。

整流器由于造价便宜，安装方便，整流效果显著，在流量测量中得到了广泛的应用。各国学者也进行了较为系统的理论和实验研究[1-9]。随着计算流体动力学的发展，数值计算方法逐渐应用于整流器的研究中[10-13]，以代替部分实验，节省研究成本。目前，国内关于此问题的研究相对较少。

笔者对整流器的数值模拟进行了研究。利用数值计算手段分别研究了Laws整流器和NEL整流器的内部流场，流体干扰源为不在同一平面内的双弯头；并利用文献[3]中的实验结果对数值计算结果的有效性进行验证。

1 数值计算模型

整流器内部流场的基本控制方程组为连续性方程：

(1)

和N-S运动方程：

(2)

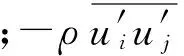
由于雷诺应力的引入，基本控制方程组需结合紊流模型方程构成封闭方程组。整流器的数值模拟中，紊流模型选用标准k-ε双方程模型的有效性已得到证实[13]。文中，模型方程中相关系数取值分别为：Cμ=0.09，C1=1.44，C2=1.92，σk=1.0，σε=1.3。

考虑到固体壁面区域，雷诺数较低，紊流发展不充分，特别是粘性底层，流动几乎是层流，紊流切应力也就不起作用，故在近壁点采用壁面函数法来改善近壁区域的计算结果。

为了提高计算精度，空间方向上采用二阶迎风格式离散所有的控制方程，同时选用SIMPLE算法作为压力-速度耦合算法；时间方向上采用二阶时间步进格式来进行时间离散。

至于计算区域的边界条件，确定如下：进口为圆管紊流充分发展流速分布，凡与流体相接触的所有固体界面上采用无滑移固体壁面条件，出口给定静压。

2 计算结果与分析

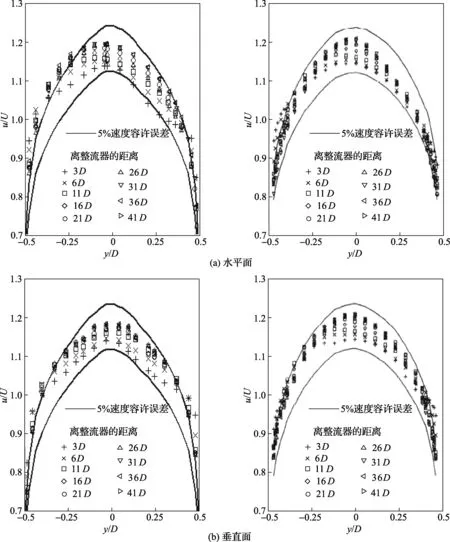
图1 Laws整流器下游轴向流速分布

主要对Laws整流器和NEL 整流器的数值模拟进行了研究，它们的结构参数见表1，表中参数D为管道的直径。计算中涉及到的所有参数值同文献[3]中的实验，即流体干扰由不在同一平面内的双弯头所产生，整流器布置在离第二个弯头4D距离处，计算介质为水，圆管直径D为102.6mm，流量为40L/s。双弯头后直管段的长度为50D。需要解释的是，文献[3]的实验系统中，双弯头前为77D长的直管段，而且离双弯头27D处布置了MHI整流器，以保证进入双弯头前的流体为充分发展流。故在数值模拟中，双弯头前设置了5D长的直管段，同时考虑到文献[3]中提供的5%速度容许差上限的最大值约为1.24倍管截面平均流速，下限的最大值约为1.13倍管截面平均流速，故进口流速设为符合1/8.5律分布的充分发展流。

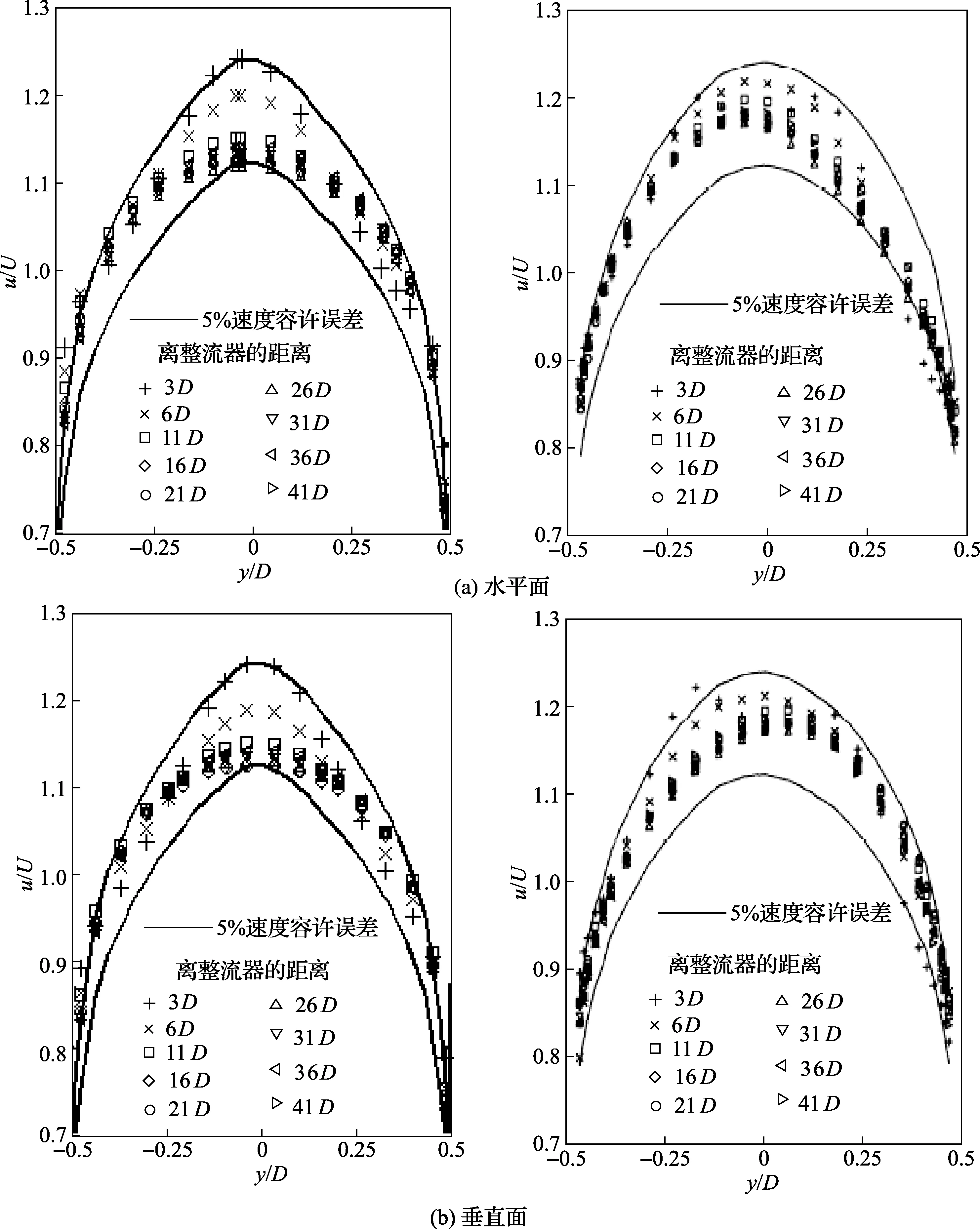
图2 NEL整流器下游轴向流速分布

划分网格时，整流器及其前、后1D管段内采用四面体网格划分，计算区域的其他部分则采用结构网格划分。以Laws整流器为例，整个计算区域内的网格总数为195万。

图1为Laws整流器下游不同管段处轴向流速的计算值和实验值的比较，分别取了水平面和垂直面两个面进行比较，其中左边为计算值，右边为实验值。图中横坐标y/D表示的是所取面上某一点到轴心的距离与管道直径的比值，纵坐标u/U表示的是所取截面上某一点的流速与管截面平均流速的比值。从图1可以看到，计算结果所反映的整流器下游轴向流速的发展规律和实验结果所反映的比较相吻合，而且垂直面上计算值和实验值相当吻合，但是水平面上计算结果得到的轴向流速剖面要略比实验结果得到的轴向流速剖面“扁平”，靠近管壁处，计算值大于实验值，靠近管线中心，计算值小于实验值。

图2为NEL整流器的计算值和实验值的比较。从图中可以看到，计算值和实验值相差并不大，但是计算值并没有刻画出实验值所显示的非对称分布。和前面对Laws 计算结果一样，计算得到的轴向流速剖面要比实验结果显示的轴向流速剖面“扁平”。估计造成上述计算误差的主要原因是网格划分得不够细。从该图中同时可以看到，和实验结果一样，计算结果显示在整流器下游6D后，轴向流速分布满足5%速度容许误差。

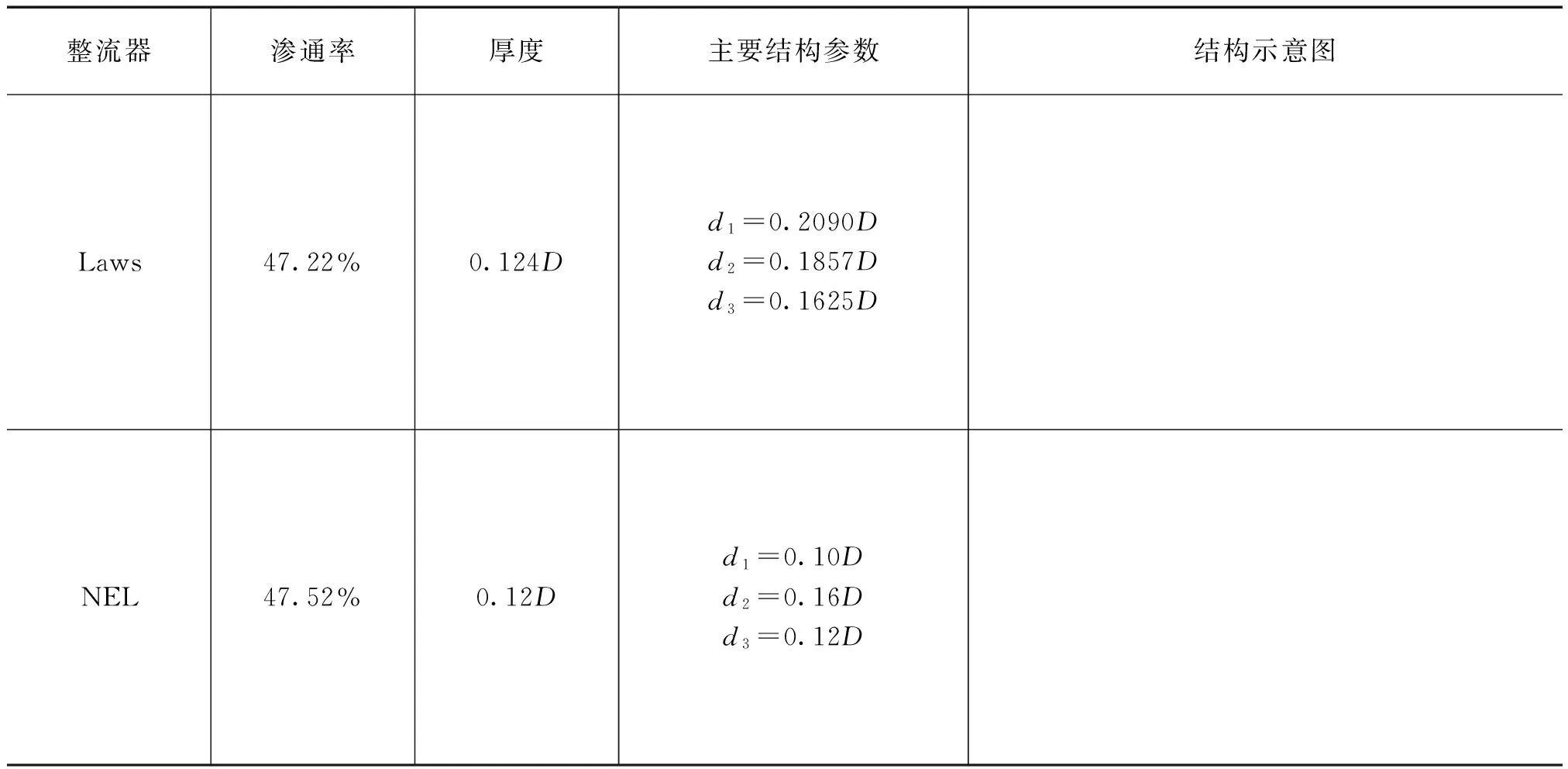
表1被研究整流器的相关参数值

3 结论

本文利用数值计算方法对文献[3]中有关Laws整流器和NEL整流器的实验进行了计算，所得到的计算结果和该文献提供的实验结果基本上相吻合。这说明了数值计算方法可应用于整流器的优化设计，以节省研究成本，加快研究进程。

[1] Ouazzane A K，Benhadj R.Flow conditioners design and their effects in reducing flow metering errors [J].Sensor Review，2002，22(3):223-231

[2] Morrison G L，Hall K R，Holste J C，et al.Flow development downstream of a standard tube bundle and three different porous plate flow conditioners [J].Flow measurement and instrumentation，1997，8(2):61-76

[3] Spearman E P，Sattary J A，Reader-Harris M J.Comparison of velocity and turbulence profiles downstream of perforated plate flow conditioners [J].Flow measurement and instrumentation，1996，7(3/4):181-199

[4] Laws L M，Ouazzane A K.A preliminary study into the effect of length on the performance of the Etoile flow straightener [J].Flow measurement and instrumentation，1995，6(3):225-233

[5] Ouazzane A K，Benhadj R.Flow conditioners design and their effects in reducing flow metering errors [J].Sensor review，2002，22(3):223-231

[6] Laws E M，Harris R.Evaluation of a swirl-vor-tab flow conditioner [J].Flow Measurement and Instrumentation，1993，4(2):101-108

[7] Dijstelbergen H.Optimal Straightening Vanes for Turbine Meters [C].presented and published，Proceedings of the 3rd International Symposium on Fluid Flow Measurement，San Antonio，Texas，March 1995:1-14

[8] Laws E M，Quazzane A K.A further study into the effect of length on the Zanker flow conditioner [J].Flow measurement and instrumentation，1995，6(3):217-224

[9] Lundberg Don.Effects of flow conditioning on liquid measurement [C].Proceedings of the 76th International School of Hydrocarbon Measurement，Oklahoma City，Oklahoma，May 2001:175-181

[10] Frattolillo A，Massarotti N.Flow conditioners efficiency a comparison based numerical approach [J].Flow measurement and instrumentation，2002，13(1):1-11

[11] Buonanno G，Delllsola M，Strutture，et al.Numerical analysis of flow conditioner efficiency [C].Proceedings of FLOMEKO 2000，Salvador，Brazil，2000:1-10

[12] Aichouni M，Laribi B.Computational study of the aerodynamic behavior of the laws vaned plate flow conditioner [C].Proceedings of the FEDSM2000 2000 ASME fluids engineering conference，Boston，USA，2000:275-279

[13] Erdal A.A numerical investigation of different parameters that affect the performance of a flow conditioner [J].Flow measurement and instrumentation，1997，8(2):93-102