大型工件感应加热的有限差分模型分析

王秀莲，曹 宏，周光远，藤金辉

(沈阳理工大学 1.信息科学与工程学院;2.经济管理学院，辽宁 沈阳 110159)

感应加热过程具有加热速度快、环境污染少，易实现自动化生产等特点。感应加热过程的数值分析，为实际加工过程中工艺参数的合理选取和工艺线路的确定提供了理论依据，大大降低了生产成本。

感应加热计算方法有积分方程法、边界元法、有限元法和有限差分法等［1－3］。航空工业部第五设计院干肇智［1］用有限差分方法对感应加热工件温度分布进行模拟，但其有限差分方法求出的电磁场和温度场的迭代矩阵都是非正定的，程序编制的工作量大;杭国平［2］等人采用有限元法计算感应加热温度分布，但其离散方法复杂，计算成本高;张媛媛［3］采用边界元法进行感应加热分析，其基础是积分方程控制误差困难。本研究来源于圆柱体型工件热处理生产实际，在工件热处理过程中，利用有限差分模型，并基于 VS2008软件C++计算程序，计算感应加热过程中温度分布，实时控制感应加热过程，热处理温度达到要求，可及时停止感应加热处理。程序简单有效，计算速度快，易于对加热过程进行控制。

1 模型建立

1.1 感应加热原理

感应加热实质是利用电磁感应在导体内产生的涡流发热加热工件过程。当感应加热的线圈中通过交变电流时，在线圈内部和其周围产生一个交变磁场，感应加热时，工件被交变的磁力线切割。根据电磁场理论，变化着的磁场产生感应电动势，感应电动势在工件表面形成封闭的电流回路，通常把这种电流称为涡流。涡流在工件内部产生热量，使工件得到加热。

1.2 渗透层

由于电磁场的集肤效应，感应加热过程中存在电流透入层，感应电流集中于该层，提供感应加热大部分能量，决定了最终的加热效果，这个深度便是感应加热的“渗透层深度”。涡流的理论渗透层深度 h(m)为［4］

式中:ρ为工件材料的电阻率(Ω·m);μr为工件材料的相对导磁率;μ0为真空磁导率，μ0=4π×10－7H/m;f为电流的频率(Hz)。

1.3 模型建立

大型工件在加热过程中其温度场随时间变化而变化。假设工件沿不同方向的导热系数为常数，采用显式有限差分方法，导出感应加热的有限差分模型。取平行六面体微元做控制体，应用热力学第一定律［5］，可得关于温度T的通用导热方程

式中:T为x、y、z和时间t的函数;λ为导热系数;ρ为密度;c为比热容;q为内热源。将其转换至圆柱体坐标系下，可得圆柱体坐标系下的导热方程

考虑圆柱体加热时的径向对称性，可按二维(z，r)不稳定圆柱体导热模型处理，得导热模型如下:

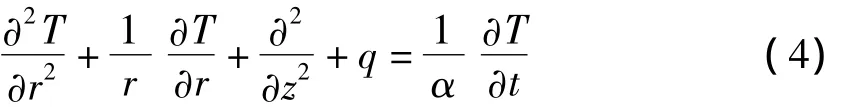
式中α=λ/ρc为热扩散系数。将圆柱体按轴向和径向离散化，划分成不同的离散单元。考虑T在(β，τ)点处的偏导数，使用前向有限差分［4］可得有源非稳态二维圆柱体坐标下导热的显式差分模型:

式中:i=1，2，…，(nz－1)，nz为圆柱体轴向离散化后的分段数;j=1，2，…，(nr－1)，nr为圆柱体径向离散化后的分层数;n表示当前时刻，(n+1)表示下一时刻;Δz、Δr代表离散单元的轴向和径向长度。

2 模型分析

2.1 模型计算的边界处理

在感应加热过程中其边界对流对温度计算的影响远小于边界辐射对温度计算的影响。因此，在模型计算过程中忽略对流对温度计算的影响，通过调整辐射系数的方法进行加权，可减少边界计算约束条件，又能保证计算的准确性;对于边界辐射，则采用斯忒潘－波尔兹曼定律［6］

进行计算，式中的环境温度To采用工件表面温度加权来实时更新，保证计算的准确性。

2.2 渗透层对涡流的影响

研究表明，在感应加热过程中，从工件表面到中心，感应电流的大小按照指数规律下降和变化。距离表面x处的强度为［7］

式中:Io为表面的涡流强度(A/m2);x为距离工件表面的距离(m);h为渗透层深度(m)。分析可知，渗透层深度主要由相对磁导率和频率［8］决定。当频率一定的情况下，相对磁导率成为影响渗透层深度主要因素;当离散点温度高于居里点温度［9］(750℃)时，其相对磁导率发生突变，渗透层深度变大，涡流影响范围变大。程序中使用简化计算，当离散单元的温度高于居里点温度时，即把该离散单元加入到涡流影响的范围内，统计全部有涡流的离散单元，将所有能量均分到每个离散单元中，这样既能保证计算的简单，又能保证计算精度。

2.3 模型计算在加热过程中的作用

在感应加热过程中，模型计算起主要的控制作用。根据已知的初始温度和加热电源的总功率，计算出整个加热过程所需数据，包括跟随温度变化的工件材料电阻率、磁导率、比热和密度等物性参数［10］，为准确计算下一时刻的温度提供了有效保障，直至整个加热过程完毕，得到加热过程的温度分布情况。

3 模型计算结果分析与对比

以尺寸 φ1630mm×2050mm圆柱体工件为例，工频电源额定功率P=4000kw，频率为50Hz;磁场感应效率η=0.8～0.9;圆柱体初始温度为300℃;离散化:轴向每段100mm均分，多余部分分别加在两端;径向(由表层向圆心)按照外6层每层10mm，中间3层每层20mm，其余为一层的离散方法。渗透层深度随温度的变化而变化，在10～50mm之间非线性变化;保证模型计算稳定，取最小时间步长Δt=2s。按工艺要求，以径向距离表面70mm、轴向距离底面 1025mm、温度达到800℃时，程序退出计算。模型计算过程利用VS2008环境下的C++程序完成，得到的计算结果用MATLAB绘图分析。

在离散化中采用轴向均分、径向上在表面和目标层单元格分多层的方法，因为只需控制目标层单元和表面温度，对靠近圆心的温度计算精度要求不高，这样划分既能满足工艺要求，也能简化计算，加快计算速度。

3.1 有限元方法的介绍

以变分原理为基础建立起来的有限元法是将整个区域分割成很多小的子区域，并构造定义在子区域上的简单尝试函数，将整个区域中各个子区域所对应的尝试函数线性组合起来，便形成近似解的表达式，完成计算的方法［2］。

3.2 模型计算速度分析

在满足工艺计算要求的情况下，由前面的分析和离散化可看出，有限差分模型的离散化简单，计算选取的时间步长既能保证模型的计算速度，又能保证模型计算的稳定性;模型计算过程中对边界条件和感应涡流分布的处理方法也简化了计算，提高了模型的计算速度;模型计算过程中将电磁场与温度场分开计算，减少两个场之间的耦合。而有限元方法采用ANSYS软件进行复杂的电磁场和温度场计算，其耦合计算，计算过程复杂，计算速度和计算成本比较高，不能较好地满足工业现场快速完成计算的要求。

3.3 结果分析与对比

利用有限差分程序使用MATLAB模拟出整个圆柱体中每个离散单元的温度分布，如图1所示，纵向表示圆柱体径向方向上的温度分布，横向表示圆柱体轴向方向上的温度。

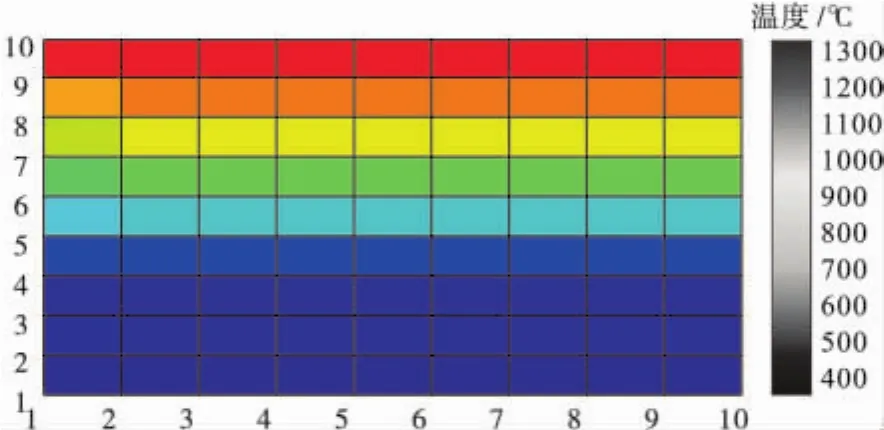
图1 圆柱体整体温度分布图

图2是有限差分圆柱体三个离散单元在感应加热过程中的温度上升情况，图中说明部分表示在圆柱体离散单元中的坐标(x，y)，x表示径向方向，y表示轴向。

图2 温度上升过程图

图3 温度对比图

图3是在相同的离散情况下分别利用有限差分算法、有限元方法和实际测温点测得圆柱体一个离散单元在感应加热过程中温度变化对比图，其中误差一表示实际温度与差分算法的误差，误差二表示实际温度与有限元算法的误差。

4 结论

(1)感应加热过程中圆柱体表面温度上升速度较快且幅度大，而内层单元格温度上升速度较慢且幅度小，越靠近圆柱体圆心这种现象越明显，验证了在感应加热过程中由于集肤效应的存在使感应电流集中于圆柱体表面，内层则靠导热来进行温度传递。

(2)在满足实际工程要求的前提下，采用有限差分模型计算感应加热的温度分布情况比采用有限元方法离散化简单，使用程序易于实现，计算程序简单有效，计算速度快、成本较低。

(3)在感应加热过程中可通过调整电源的功率使圆柱体表面温度最终趋于稳定，不会为达到加热目的使表面温度过高损伤工件属性。

(4)利用模型的数值解有效分析了感应加热过程中温度场的分布特性，为合理选取工艺参数提供依据;为类似感应加热热处理过程计算提供简单有效的计算方法，并为控制感应加热过程提供有益参考。

(5)在相同的前提条件下，采用相同的离散化方法，采用有限差分方法比采用有限元方法计算感应加热温度分布更接近实际温度分布情况，且满足工程精度要求，可指导现场生产实践。

［1］干肇智.感应加热的数值计算［J］.电炉，1985(5):1－12.

［2］杭国平.感应加热问题的有限元分析［D］.上海:上海大学，1991.

［3］张媛媛.基于有限元和边界元方法的轴类感应加热分析及数值模拟［D］.天津:天津大学，2006.

［4］赵长汉，姜士林.感应加热原理与应用［M］.天津:天津科技翻译出版公司，1992.

［5］D.皮茨.L西索姆.全美经典－传热学［M］.葛新石等译.北京:科学出版社，2002:1 －9，69 －78.

［6］陶文铨.数值传热学［M］(第二版).西安:西安交通大学出版社，2001.

［7］金晓昌.感应加热技术中的趋肤效应［J］.武汉化工学院学报，1995，17(4):65 －68.

［8］刘白.双频感应淬火的计算与应用［J］.贵州工业大学学报(自然科学版)，2001，30(4):20 －24.

［9］Fireteanu，Tudorache T.Electromagntic forces in transverse flux induction heating［J］.IEE Transactions on Magneties，2000，36(4):1792 －1795.

［10］Kawase Y，Miyatake T.Thermal analysis of steel blade quenching by induction heating［J］.IEEE Transactions on Magnetics，2000，36(4):1788 －1791.