无超调不限阶数的M型次多容惯性标准传递函数
杨 平,陈式跃
(1.上海电力学院电力与自动化工程学院,上海 200090;2.上海量值测控仪器科技有限公司,上海 200090)
0 引 言
在众多的控制器设计方法中,标准传递函数设计法[1]的简捷性最引人注目。只要已知受控过程模型和确定了期望标准传递函数,那么控制器可通过简单的代数运算来设计。标准传递函数设计法的核心是取控制系统的期望传递函数为选定的标准传递函数。最早提出也是最常用的标准传递函数是ITAE标准传递函数[2]。比ITAE标准传递函数晚8年提出的Butterworth标准传递函数[3]可算是仅次于ITAE标准传递函数的第2种常用标准传递函数。近年来,有关标准传递函数本身的研究也出现了一些新进展。在我国,已有不少研究[4-8]对两种常用标准传递函数提出改进。这些改进研究所改变的主要是标准传递函数的系数数值。所采用的改进方法有:缩短积分时间域、重新优化计算、选用遗传算法来优化等。改进的效果主要体现在超调量的减少。与改进研究不同,文献[9]则提出了一种新标准传递函数,称为多容惯性(multiple capacity process,MCP)标准传递函数。这种新的标准传递函数具有系统无超调和不限系统阶数的特点,并且在工程应用上的通用性更强。不过,文献[9]的阐述还不够完善,只给出了1型的多容惯性标准传递函数。本文的研究是文献[9]工作的继续,将给出任意系统阶数的M型次的多容惯性标准传递函数,并且更深入地分析了多容惯性标准传递函数的动态特性和探讨了其工程应用方法。
1 M型次多容惯性标准传递函数构建方法
根据基本的控制理论[1],控制系统的稳态准确性取决于控制系统的型次。若要使某控制系统在阶跃输入下无稳态误差,则要求该系统的型次至少大于0。若要求系统在斜坡输入下也无稳态误差,则要求系统的型次至少大于1。所以,标准传递函数应该有不同的系统型次之分。常见的ITAE标准传递函数就有1型和2型两种,而且这两种函数的同幂项系数是不同的。文献[9]只给出了1型的多容惯性标准传递函数的构建方法。现给出适用于任意系统型次的多容惯性标准传递函数的通式:
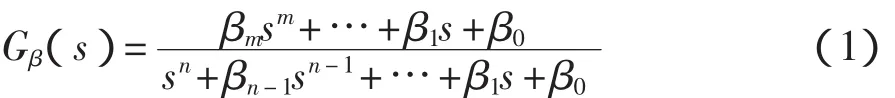
式中:n——多容惯性标准传递函数分母多项式的阶数,也是系统的阶数;
m——多容惯性标准传递函数分子多项式的阶数;
βi——多容惯性标准传递函数多项式的系数。
可以注意到,分母多项式和分子多项式的同幂项系数是相同的,这一点与ITAE标准传递函数是相同的。但是,与ITAE标准传递函数不同的是,多容惯性标准传递函数的多项式系数并不随系统型次的改变而改变。因此,一旦系统阶数和惯性单元时间常数确定,多容惯性标准传递函数的多项式系数就确定了,并与所期望的系统型次无关。
式(1)所描述的多容惯性标准传递函数系统的型次为

也就是说,多容惯性标准传递函数分子多项式的阶数m应由所期望的系统型次来确定,即

多容惯性标准传递函数的多项式系数βi,可用式(4)计算:
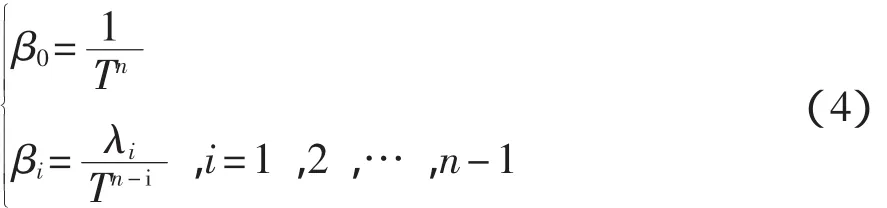
式中:T——惯性单元时间常数;
{λi,i=1,2,…,n-1}——代数二项式系数。
导出多容惯性标准传递函数的多项式系数βi的计算式(式(4))的思路是视系统为多个惯性单元串联而成。设m=0,令
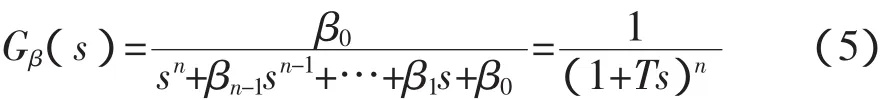
可据代数二项式定理导出
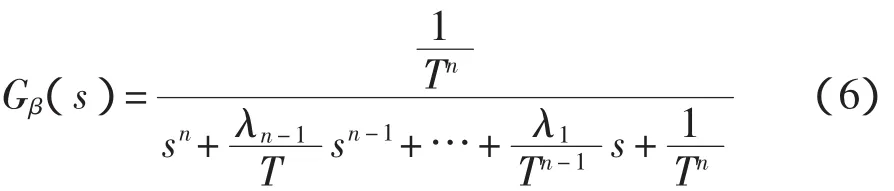
再整理系数并推广至m≠0,即得式(4)。
惯性单元时间常数T的确定公式如式(7)所示。该式为经验公式,依据是一阶惯性环节的过渡过程时间ts为惯性时间T的3倍(按达到终态值的95%计算),即ts=3T;以及n阶惯性环节的过渡过程时间ts可按ts=3nT估计[10]。

根据代数学中的二项式定理,可求得代数二项式系数{λi,i=1,2,…,n-1}如表 1 所示。由系统阶数n可确定表1中的行序。表1所示的三角形数阵为著名的杨辉三角形数阵中不含1的内核部分。每行系数值的推算都遵循一个简单的规则:(1)左右两端的系数值为阶数n;(2)中间的每个系数值为上一行相邻的两个系数值之和。例如,n=4行的系数值6可用n=3行的相邻系数3+3得出,n=5行的系数值10可用n=4行的相邻系数4+6得出,以此类推。表1只给出15阶及以内的各系数值。事实上,依据上述简单的推算规则,很容易推算出任意高的系统阶数数值下的系数值。

表1 多容惯性标准传递函数中的系数λi
2 多容惯性标准传递函数的系统型次论证
上节所述的多容惯性标准传递函数(式(1))的系统型次是否为M可如下论证:
对于系统Gβ(s),设输入为R(s),输出为Y(s),则有误差函数E(s)(见式(8))。代入Y(s)和Gβ(s),则可导出的误差函数的计算式(式(10)),进而导出稳态误差的计算式(式(11))。
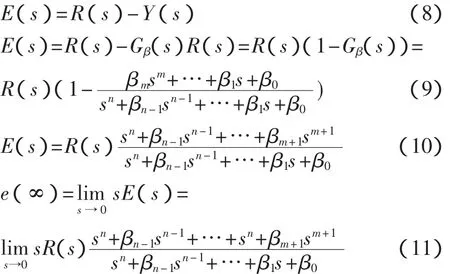
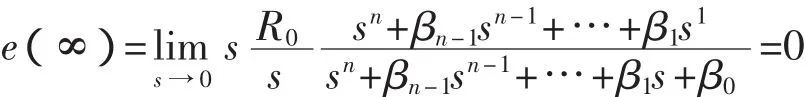
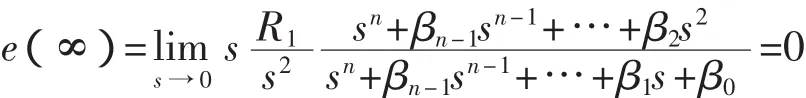
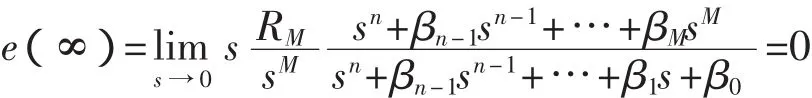
由此可见,由多容惯性标准传递函数定义的系统Gβ(s),只要取m=M-1,则Gβ(s)的系统阶数为M。
3 多容惯性标准传递函数特性分析
3.1 1型系统的阶跃响应
设系统型次M=1,设惯性单元时间T=1,分别取系统阶数为2,4,6,则有1型多容惯性标准传递函数为
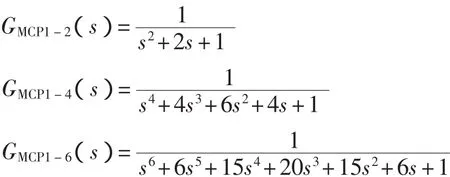
再设惯性单元时间T=0.5,系统阶数n=6,有1型多容惯性标准传递函数为
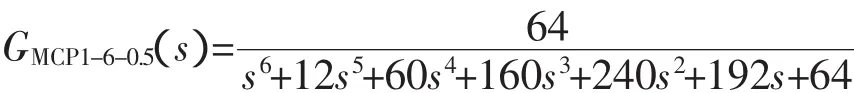
为了比较,取自然振荡频率ωn=1,据文献[1]中表4-5,算得1型6阶的ITAE标准传递函数为
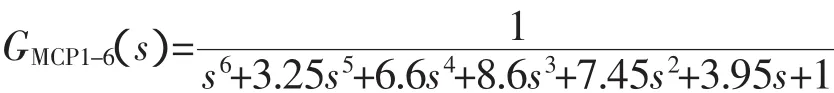
利用Matlab/Simulink动态系统仿真平台,可得上述5种系统的单位阶跃响应和误差响应如图1和图2所示。按达到终态值的95%为线,从误差响应图上可测得5种系统的调整时间值如表2所示。
从图1和图2以及表2可看出:(1)在惯性单元时间T=1条件下,多容惯性标准传递函数所述系统的调整时间ts与系统阶数n成正比关系,基本符合式(7)所述关系;(2)多容惯性标准传递函数所述系统的响应没有超调;(3)在系统阶数n=6条件下,ITAE标准传递函数所述系统的调整时间ts可能比多容惯性标准传递函数所述系统长(T=1时),也可能比多容惯性标准传递函数所述系统短(T=0.5时)。换言之,通过调整T值的大小可获得系统调整时间的期望值。
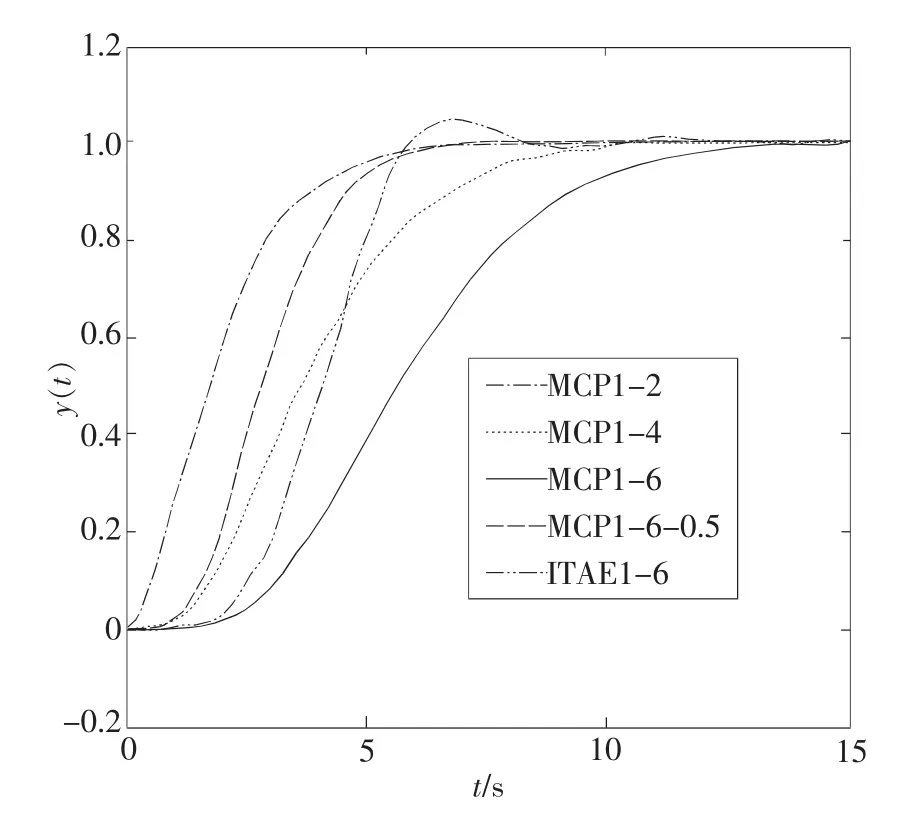
图1 1型标准函数系统的阶跃响应
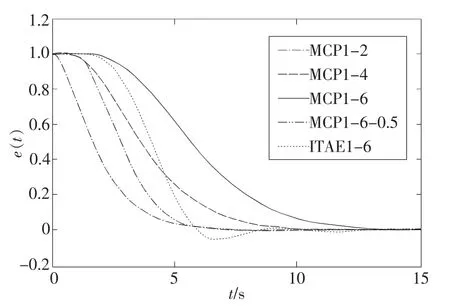
图2 1型标准函数系统的阶跃响应误差

表2 t s的计算和实测
表2不但给出了5种系统的调整时间测得值,还给出了对应的计算值。比较这些数值,可知实测值均小于计算值,而且是阶数越高,差值越大。不过从留有余地的保守性设计角度出发,这种误差还是可以接受的。
3.2 2型系统的斜坡响应
设系统型次M=2,设惯性单元时间T=1,分别取系统阶数为2,4,6,则有2型多容惯性标准传递函数为
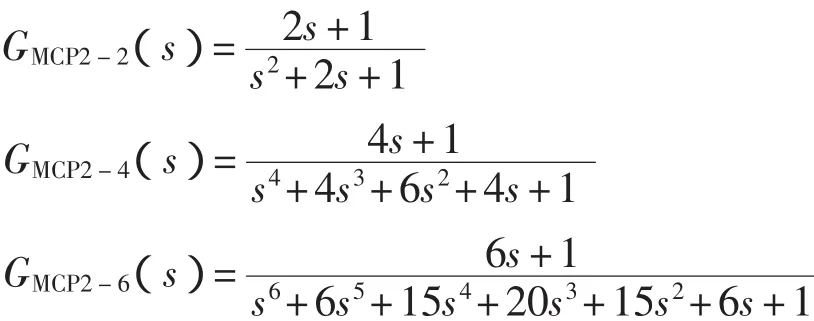
再设惯性单元时间T=0.5,系统阶数n=6,有2型多容惯性标准传递函数为
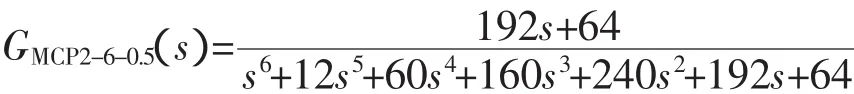
为了比较,取自然振荡频率ωn=1。据文献[2](Graham&Lathrop)中的ITAE标准传递函数数据,算得6阶的2型ITAE标准传递函数为
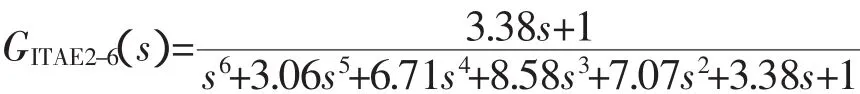
利用Matlab/Simulink动态系统仿真平台,可得上述5种系统的单位斜坡响应和误差响应如图3和图4所示。
从图3和图4同样可看出:多容惯性标准传递函数所述系统的斜坡响应也像阶跃响应一样没有超调;其过渡过程时间与阶跃响应中定义的调整时间相当;在n=6条件下,ITAE标准传递函数所述系统的过渡过程时间比多容惯性标准传递函数所述系统时的要长,比T=0.5时要短。
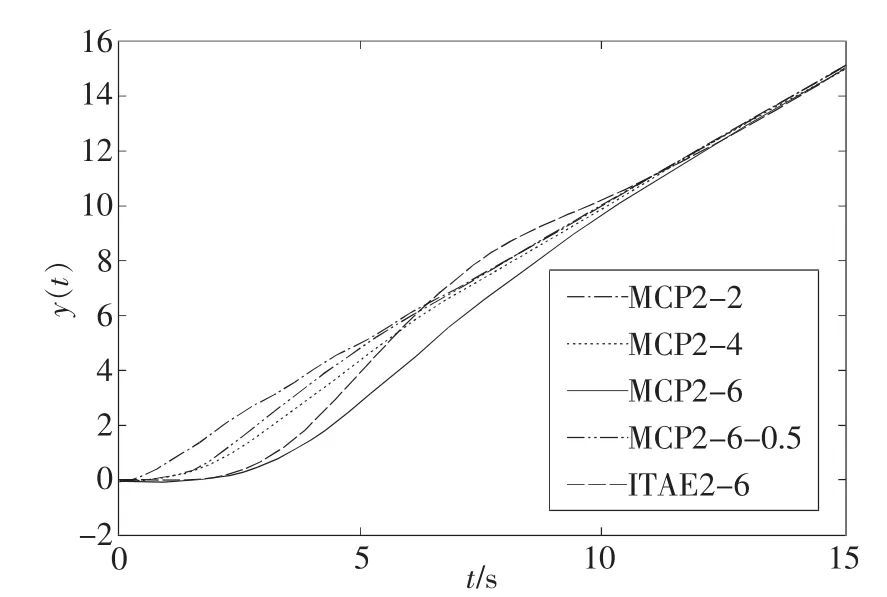
图3 2型标准函数系统的斜坡响应
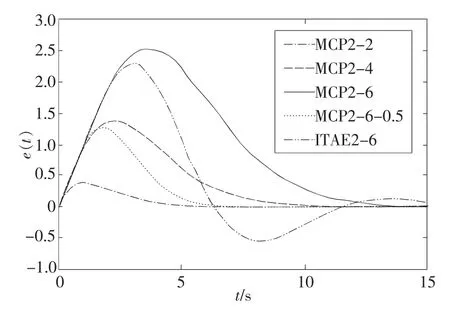
图4 2型标准函数系统的斜坡响应误差
4 多容惯性标准传递函数的应用探讨
在文献[11]中,专门讨论了应用标准传递函数设计控制器的理论方法,考虑了串联校正型、反馈校正型和状态反馈型控制器的设计问题。并且针对1型标准传递函数无零点的特点,分别导出了串联校正型、反馈校正型和状态反馈型控制器的设计约束条件。还针对有零点的被控过程提出了应用直接设计法和补偿法两种解决方案。
在文献[12]中,专门讨论了应用多容惯性标准传递函数设计状态反馈型控制器的问题,也是应用无零点的1型标准传递函数。由于状态反馈型控制器不会增加系统零点,所以更易满足无零点约束条件。此外,在文献[12]中所述的被控过程本身的阶数高达9阶,若采用ITAE标准传递函数,则找不到数据,而用多容惯性标准传递函数,其不限阶数的优势尽现。
M型次的多容惯性标准传递函数的提出,打破了1型多容惯性标准传递函数的应用局限,为应用标准传递函数设计控制器提供了更大的设计空间。例如,针对2型标准传递函数,控制器的设计约束条件将从无零点变为可有一个零点,所设计系统的型次也从1型提高至2型。
以下以管式检定炉的温度控制为例,应用1型多容惯性标准传递函数设计一个串联校正型控制器。
考虑图5所示的典型的串联校正型控制系统。其中,Gc(s)是控制器传递函数,Go(s)是被控过程传递函数,R是系统的设定值输入,Y是系统输出。系统总的传递函数W(s)如式(12)所示。
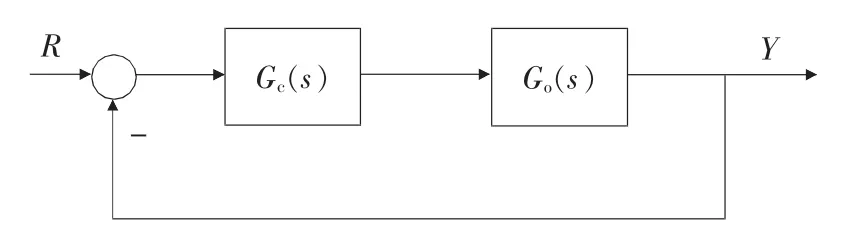
图5 串联校正型控制系统
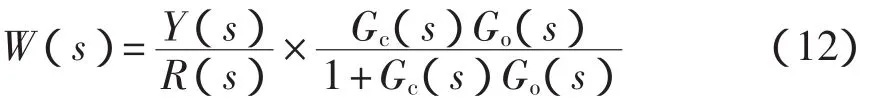
应用直接设计公式式(13)可得控制器Gc(s)。
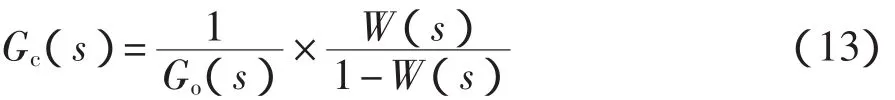
假设已知被控过程管式检定炉的数学模型[13]如式(14)所示,这是一个有零点的被控过程。
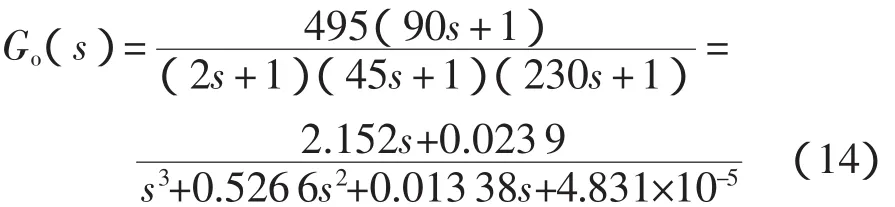
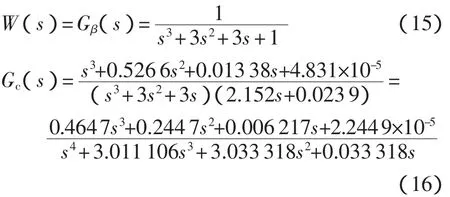
利用Matlab中的simulink平台,可搭建相应的仿真试验系统。将利用直接设计公式设计的多容惯性标准传递函数控制器Gc(s)置入试验系统,并与一个常规的PID控制系统(设PID参数为Kp=0.6,Ti=2.04,Td=4)同时进行阶跃响应试验,可获得如图6所示的阶跃响应曲线。其中,短划线是期望的标准传递函数响应,实线曲线是PID控制响应,点划线是所设计的控制系统响应。显然,所设计的控制系统响应曲线与标准传递函数响应曲线完全重合,其无超调量和调整时间短的特性远比PID控制响应优越。
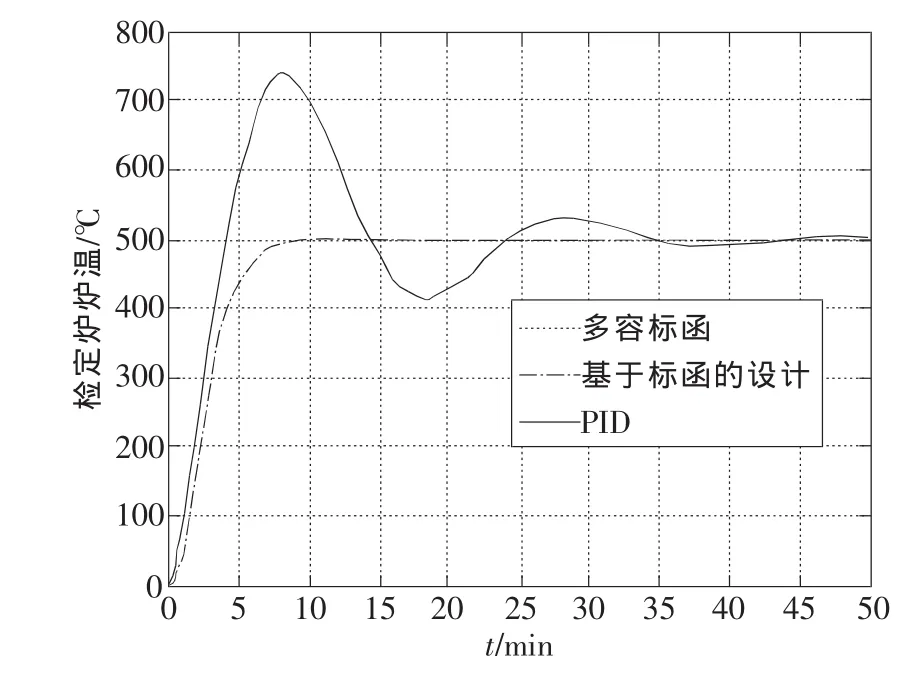
图6 检定炉温度控制响应
5 结束语
与ITAE标准传递函数相比,以上提出的通用的多容惯性标准传递函数具有无超调和不限系统阶数的鲜明特点。通用多容惯性标准传递函数的系统型次为M已得到论证。而且,构建任意数值的系统型次的多容惯性标准传递函数非常容易。多容惯性标准传递函数所表达的系统的阶跃响应和斜坡响应特性分析,充分展示了无超调特性和调整时间与3nT成正比的关系。应用通用的多容惯性标准传递函数进行控制器的设计方法讨论表明,利用控制器直接设计公式和状态反馈极点配置是两种常用的简单和有效的应用方法。
[1]杨平,翁思义,郭平.自动控制原理-理论篇[M].北京:中国电力出版社,2009:147-155.
[2]Graham D,Lathrop R C.The Synthesis of optimum transient response criteria and standard forms[J].A IEE Trans,1953(72):273.
[3]Schultz W C,Rideout C V.Control system performance measures:past,present and future[J].IRE Trans Automatic Control,1961,26(22):.
[4]杨益群,项国波.新的ITAE最佳传递函数标准型[J].信息与控制,1999,26(4):259-265.
[5]李镇铭.环路法及最佳状态反馈系统设计[M].北京:国防工业出版社,1988:120-134.
[6]张志涌,刘瑞桢.对经典ITAE传递函数标准型的研究[J].福州大学学报,1977,25(3):120-121.
[7]李钟慎.位移无静差最优传递函数的研究[J].自动化博览,2007(2):82-84.
[8]洪健,李钟慎.改进的Butterworth最佳传递函数标准型[J].计算技术与自动化,2005,24(2):13-15.
[9]杨平,余洁,孙宇贞.多容惯性标准传递函数的建立与比较[J].上海电力学院学报,2011,27(5):512-514,518.
[10]李旭.过热汽温的动态特性与控制[J].动力工程,2007,27(2):23-28.
[11]杨平.控制器的标准传递函数设计方法[J].化工自动化及仪表,2010,37(11):9-13.
[12]杨平,张玲芳,于会群.锅炉汽温状态反馈控制器的标准传递函数设计方法[J].热力发电,2011,40(1):35-39.
[13]杨平.管式电阻炉的动态特性[J].上海电力学院学报,1986(2):25-30.

