基于独立分量分析的高速微铣削力混合信号噪声分离方法
李一全,孙 岳,董山恒,于占江,于化东,许金凯
(长春理工大学机电工程学院,吉林 长春 130022)
0 引 言
随着航空航天、国防工业、微电子行业、现代医学等领域的发展,对尺寸特征在10μm~5mm的高精度三维微小零件的需求日益迫切,高速微铣削作为高精度三维精密微小零件加工的一种主要方式受到越来越多的关注。而微铣削力信号中包含了丰富的微铣削加工状态信息,因此对微铣削力信号的分析也成为了研究高速微铣削加工的重要方面。但是由于微铣削力较小,受机械噪声、环境噪声等影响明显,通过测力计采集到的观测信号均为小信噪比的铣削力混合信号,仍然按照对常规铣削的大信噪比混合信号分析方法进行分析明显是不适合的,所以从测力计采集到的观测信号中获得微铣削力信号并分离出噪声信号是必要的。而传统的如小波变换等方法大多只能起到抑制高斯噪声的作用,无法实现真正意义上的分离,这对于含有非高斯性成分的高速微铣削力混合信号的分离并不合适[1]。
目前,独立成分分析法(independent component analysis,ICA)广泛应用于发动机故障诊断、爆破信号分离、内燃机振声信号分离、变压器部件振动信号分离等领域[2-4],但将其用于高速微铣削力混合信号分离方面还鲜有研究。K.Zhu,G.S.Hong等[1]将ICA方法引入微铣削力混合信号去噪的研究当中,并且与传统的小波变换作比较,得出了在铣削力信号分离的问题上ICA方法优于小波变换的论断,为ICA应用于微铣削力混合信号分离的后续研究奠定了一定的基础。胥永刚等[5]将ICA引入到机械设备振动信号的分离中,为机械设备的状态监测和故障诊断提供了新方法,邵华等[6]先是利用ICA结合小波变换对70 r/min的常规铣削力信号进行分离处理,再应用FFT对信号进行识别,并且得到了较好效果。但在高速微铣削中,微铣削力受噪声干扰程度及主要噪声来源都与常规铣削有很大不同,需要进一步进行研究。
本文利用基于盲源分离理论的独立成分分析法结合快速傅里叶变换(FFT)对Kistler9256CQ01测力计采集到的微铣削力混合信号进行分离和识别,得到相互独立的微铣削力信号和噪声信号。利用ICA理论同时分离非高斯信号和高斯信号,弥补传统处理方法只抑制高斯信号的不足,验证ICA方法应用于高速微铣削力混合信号分离的可行性。
1 基本理论
1.1 ICA基本模型
ICA的基本模型表达形式为

式中:x——N维观测矢量,x=[x1,x2,x3,…,xN]T;
s——M维独立成分矢量,s=[s1,s2,s3,…,sM]T;
A——未知的N×M的混合矩阵。
ICA算法的原理就是在源信号向量s和混合信号A都未知的情况下,希望得到一个分离矩阵W,能从混合信号中分离出相互独立的源信号,即

ICA解决问题关键的一步是建立能够度量分离结果独立性的判据和相应的分离算法。ICA方法是目前应用比较广泛的盲源分离方法[7-9]。图1为线性盲源分离框图,图2为ICA模型框图。
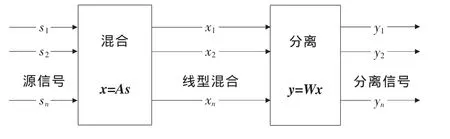
图1 线性盲源分离模型框图
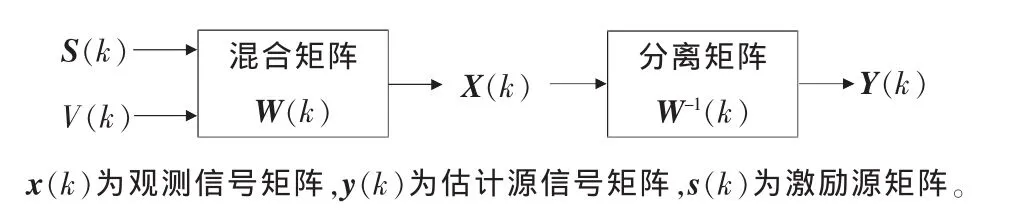
图2 ICA模型框图
1.2 微铣削力信号独立性验证和高斯性分析
应用ICA对铣削力信号进行分离时,必须满足两个条件:一是源信号必须具有独立性;二是源信号中至多只有一个为高斯信号,其余都为非高斯信号。因此,在进行ICA之前有必要对铣削力信号进行独立性验证和高斯性分析。
1.2.1 独立性验证
应用ICA分析之前,必须确保各源是相互独立的。由于铣削力、机械噪声、环境噪声等噪声都有不同的传播路径和时间周期,所以,可以近似认为各激励源之间是相互独立的,满足ICA的独立性要求。
1.2.2 高斯性分析
对于随机变量x,其峭度一般采用四阶累积量定义,即
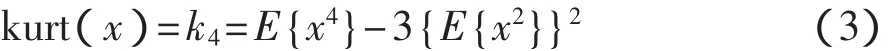
将其归一化得
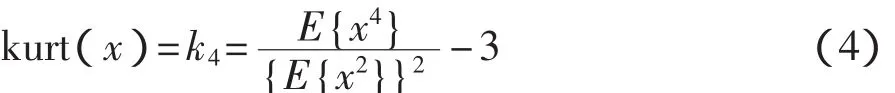
再对x进行标准化,则有E{x2}=1,式(4)可简化表示为

由式(5)及文献[3]中算法可看出,当随机变量为高斯分布时,其峭度值kurt(x)=0;对超高斯分布,其峭度值kurt(x)>0;对亚高斯信号,峭度值kurt(x)<0。与高斯信号相比,超高斯信号的概率密度函数图像峰值大,宽度窄;亚高斯信号的概率密度函数峰值小,宽度大。当信号的非高斯性越强时,峭度绝对值越大,因此可以利用峭度的大小对信号的非高斯性程度进行度量。
将含有3290个采样点的三维观测信号矩阵带入式(5),求得峭度值均大于0,图3为测力计采集的三维观测信号在7种不同工况下的峭度统计,工况如表1所示。从图3中可直观看出所有峭度值均远大于0,充分说明观测信号具有非高斯性。而根据中心极限定理,源信号的非高斯性必大于观测信号的非高斯性,因此判断源信号为非高斯性信号,符合ICA对独立源信号的非高斯性要求。
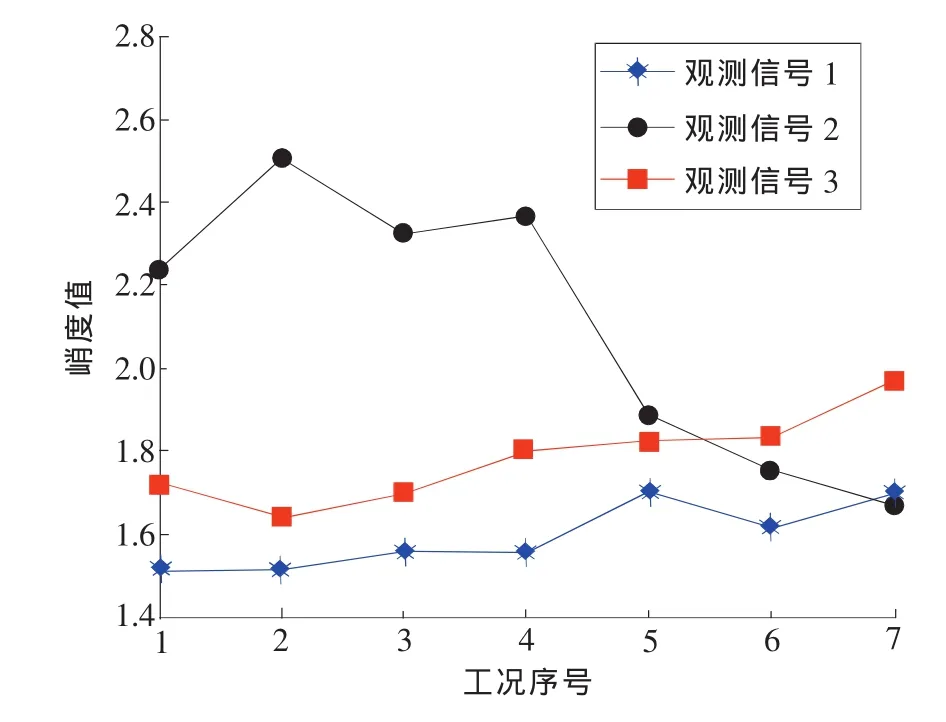
图3 峭度统计图
通过峭度对信号的非高斯性进行的验证表明,微铣削力混合信号具有非高斯性分布,可以采用ICA方法进行分离。

表1 工况详情
2 实验分析
实验采用ICA方法对铣削力混合信号进行分离。使用功率为300W的电主轴作为驱动设备,通过安装在工件下方的Kistler9256CQ01测力计对高速微铣削力进行测量。实验流程如图4所示。实验中,刀具刃圆半径、切削深度都是微米量级,实验条件已在表2中列出。
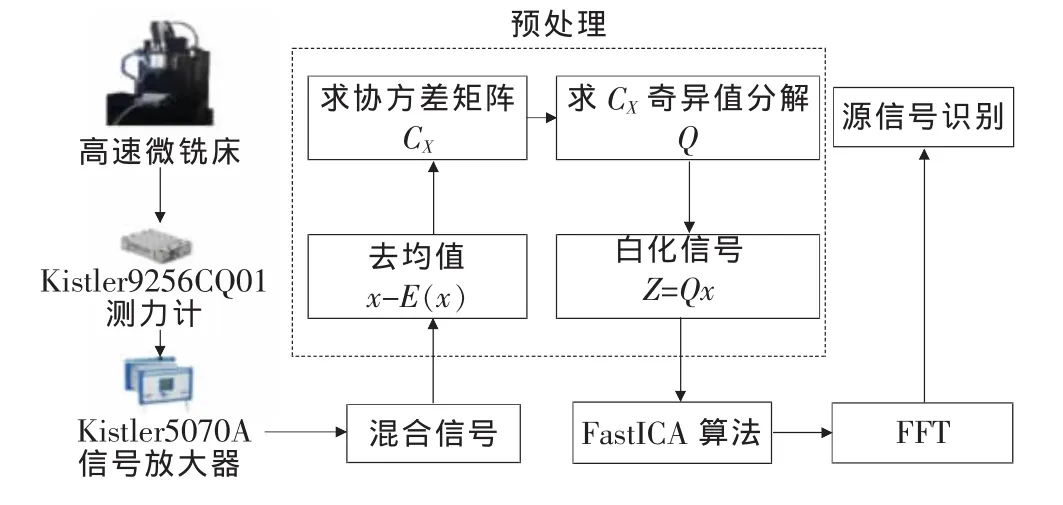
图4 微铣削力混合信号分离流程图
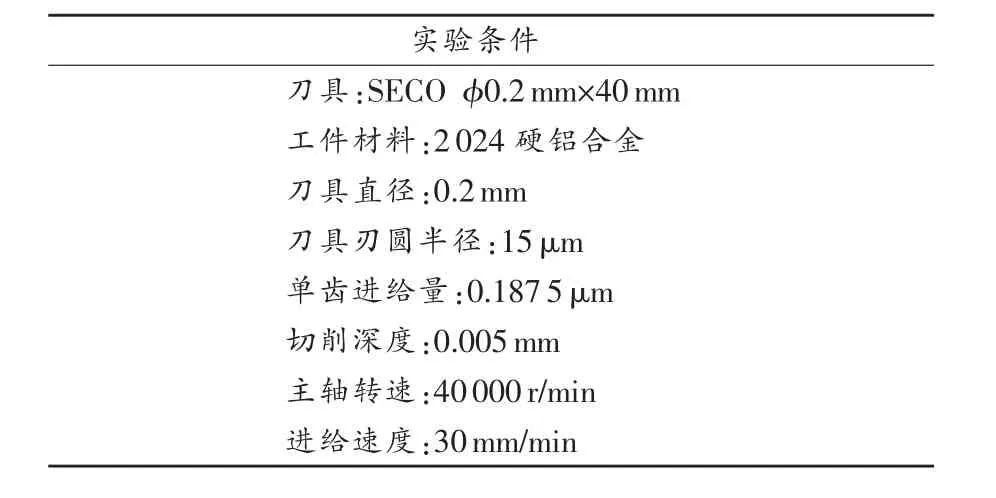
表2 实验条件
2.1 信号分析
由于加工环境较为复杂,有必要对环境噪声进行总体假设。可根据中心极限理论假设环境噪声是一个大样本的高斯噪声。通过之前对文献[1]的研究结合高速微铣削先验知识,可以近似认为所有信号有3个来源:铣削力、环境噪声、机械噪声。
假设在ICA中,3个独立源信号是加权线性混合的。独立信号加权混合的数学模型可简单表示为
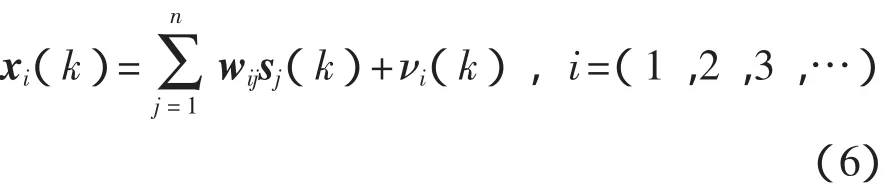
式中:xi(k)——测力计采集的观测信号矩阵;
wij——混合矩阵;
sj(k)——独立的激励源信号矩阵;
νi(k)——噪声信号。
2.2 源信号分离
实验中测力计采集得到的信号及经过FFT得到频域图象如图5所示。可以看出峰值分布较为杂乱,低频成分分布在整个时间段内,噪声混叠现象非常明显,期望得到的各独立源信号被淹没其中。由先验信息可推测,混合信号主要由微铣削力信号、具有非高斯性的机械噪声信号和具有高斯性的环境噪声信号混叠而成。可将相关的噪声也认为是独立的源信号。
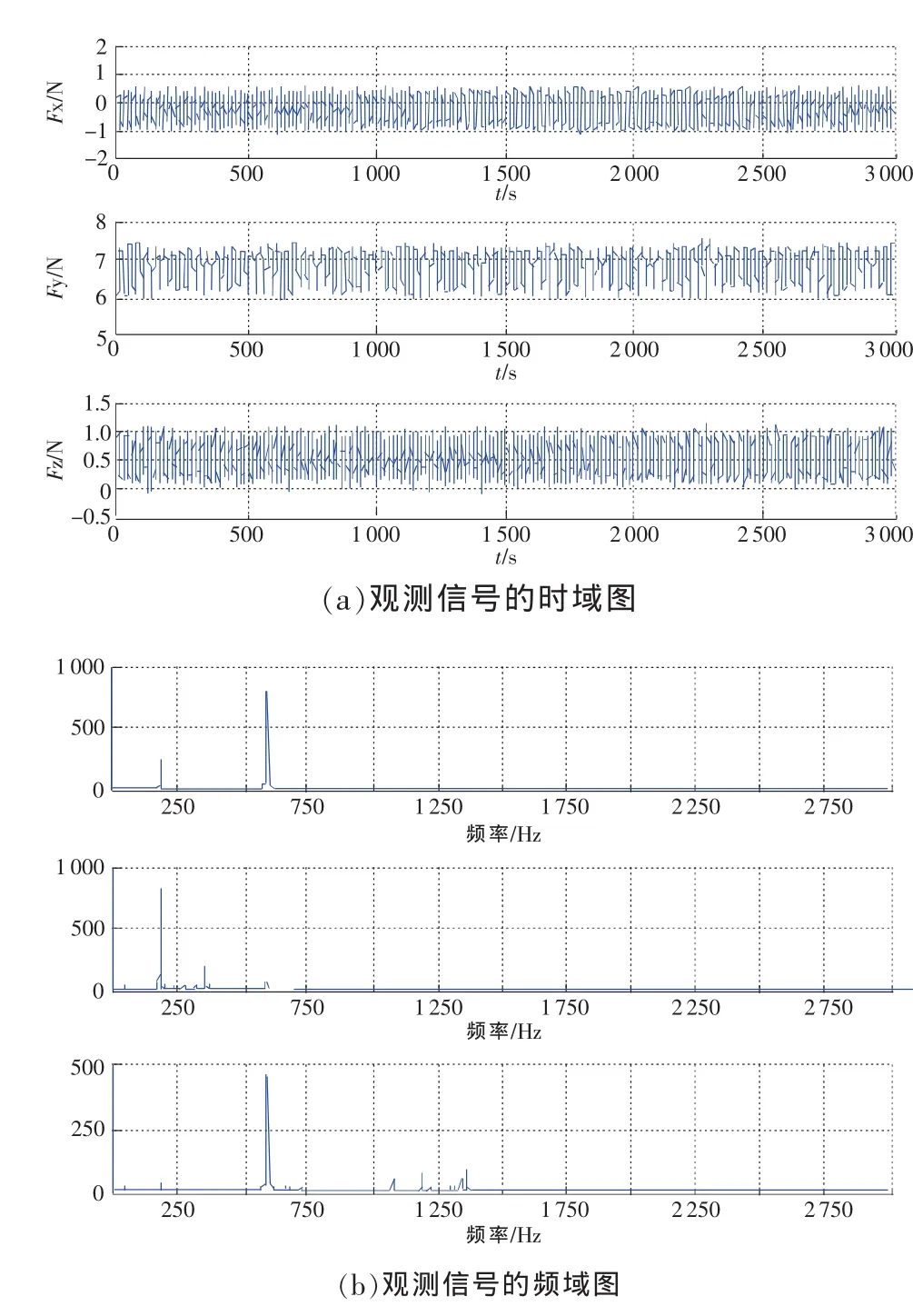
图5 测力计输出的观测信号
应用ICA方法对混合信号进行分离之前,需要对混合信号进行预处理,预处理过程主要包括中心化和预白化。首先用观测信号x减去自身的统计均值E(x),达到观测信号中心化目的。由于ICA整个过程存在式(1)所示关系,因此有

可知,观测信号x中心化后源信号s也将是零均值的。再计算观测信号的协方差矩阵Cx,并对其进行奇异值分解,得到白化矩阵Q,白化信号为

其协方差矩阵为

通过预处理过程得到各分量不相关的新的混合信号,预处理过的信号如图6所示。
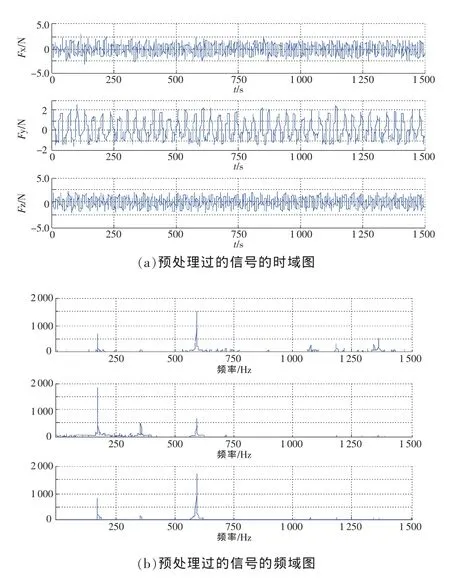
图6 预处理过的信号
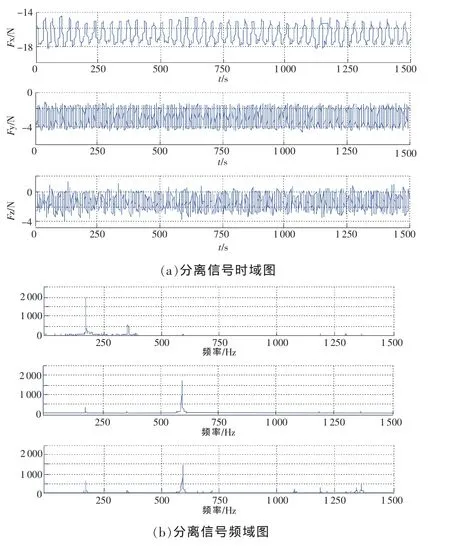
图7 分离信号
利用ICA方法对预处理过的信号进行分离后所得各独立源信号时域和频域如图7所示。可以从图中清晰的看到,经过算法中十几次迭代之后得到的一个主能量在660Hz左右独立源信号,而40000 r/min工况下的电主轴频率约为40000÷60=667Hz,两频率基本吻合,结合实验条件和文献[6]对铣削力混合信号激励源识别的研究,判断此分离后的独立源信号为微铣削力信号。分离结果中的另一个独立源信号的主要能量出现在220Hz和660Hz处,其他能量在1 000~1 500Hz处均有分布,机械噪声中660Hz左右出现的峰值判断来自主轴轴承对中性误差引起的机械振动。由于工件与铣床之间存在微小间隙,在铣削过程中会产生低频振动,由此推测机械噪声中的220Hz处的峰值正是此原因引起。结合以上分析及文献[10]的研究,此独立源信号符合高速微铣削中的机械噪声特点,判断此信号为铣削过程中的机械噪声信号。另一个独立源信号的能量全部分布在0~400Hz段内,且主能量峰出现在220Hz处。根据实际工况条件及高速加工中的环境噪声特点[6,10],结合文献[1]的研究,判断此信号为环境噪声信号。
3 结束语
本文以同时混有高斯性信号和非高斯性信号的高速微铣削力混合信号为研究对象,经过包含中心化和预白化的预处理过程后,得到各分量不相关的新混合信号。利用ICA方法对经过预处理后的新混合信号进行分离并得到独立信号,再通过FFT观察独立信号的频谱,结合先验信息对分离得到的独立信号进行识别。实验结果表明,ICA方法结合FFT能够很好的从高速微铣削力混合信号中分离各独立信号并成功对其进行识别。最终,本研究利用文中方法成功地分离并识别出了高速微铣削力信号、非高斯性的机械噪声和高斯性的环境噪声。
[1]Zhu K,Hong G S,Wong Y S,et al.Cutting force denoising in micro-milling[J].International Journal of Production Research,2008,46(15-16):4391-4408.
[2]易长平,赵明生,崔正荣.基于独立分量分析的爆破振动信号分离仿真试验[J].爆破,2010,27(1):31-36.
[3]徐红梅.内燃机振声信号时频特性分析及源信号盲分离技术研究[D].杭州:浙江大学机械与能源工程学院,2008.
[4]郑婧,何婷婷,郭洁,等.基于独立成分分析和端点检测的变压器有载分接开关振动信号自适应分离[J].电网技术,2010,34(11):208-213.
[5]胥永刚,张发启,何正嘉.独立分量分析及其在故障诊断中的应用[J].振动与冲击,2004,23(2):104-107.
[6]Shao H,Shi X H,Li L.Power signal separation in milling process based on wavelet transform and independent component analysis[J].International Journal of Machine Tools&Manufacture,2011(51):701-710.
[7]Hyvarinen A,Karhunen J,Oja E.Independent component analysis[M].New York:John Wiley&Sons,Inc,2001:130-211.
[8]李舜酩,李香莲.振动信号的现代分析技术与应用[M].北京:国防工业出版社,2008:346-392.
[9]张洁,李世云.基于独立分量分析的荧光造影图象降噪算法[J].中国测试,2012,38(3):5-7.
[10]王太勇,郭红旗,赵国立,等.车削加工噪声的产生及其控制研究[J].噪声与振动控制,1995(6):31-35.

