微小深度尺寸测量系统的误差与测量不确定度分析

齐皇仲，叶怀储，陈 欢，潘 璐，李 建

（浙江省计量科学研究院，浙江 杭州 310013）

0 引 言

项目中自制的测量系统包括电子目镜、光切显微镜、三轴运动平台以及上位机。由于该测量系统定位于工业现场测量，电子目镜和上位机可以实现电脑读数以提高测量速度，光切显微镜提供精准的测量方法，三轴运动平台模拟了工业环境中的取样送样环节，整个测量过程尽可能地还原生产现场，实现全自动测量。现场测量环境相对于实验室较为复杂多变，因此对其误差来源及测量不确定度的分析尤为重要。

1 任务目标

根据测量系统的测量原理及过程找出其中影响测量精度的误差来源，并计算其扩展不确定度。

2 测量原理

测量系统结构如图1所示。被测量的工件放置在载物台上，通过各运动轴的运动自动调整物距成像。如被测工件表面有划痕则会呈现倒三角形影像。在本测量系统中为了验证测量系统的准确度，利用量块人为制造阶梯差得到图2所示影像。通过计算成像后的像素点计算出两条光带之间的距离D，代入公式H=D×K（K为固定值，由标定得出）得到阶梯的高度。

3 数学模型分析

式中：H——测量结果；

H1——仪器读数。

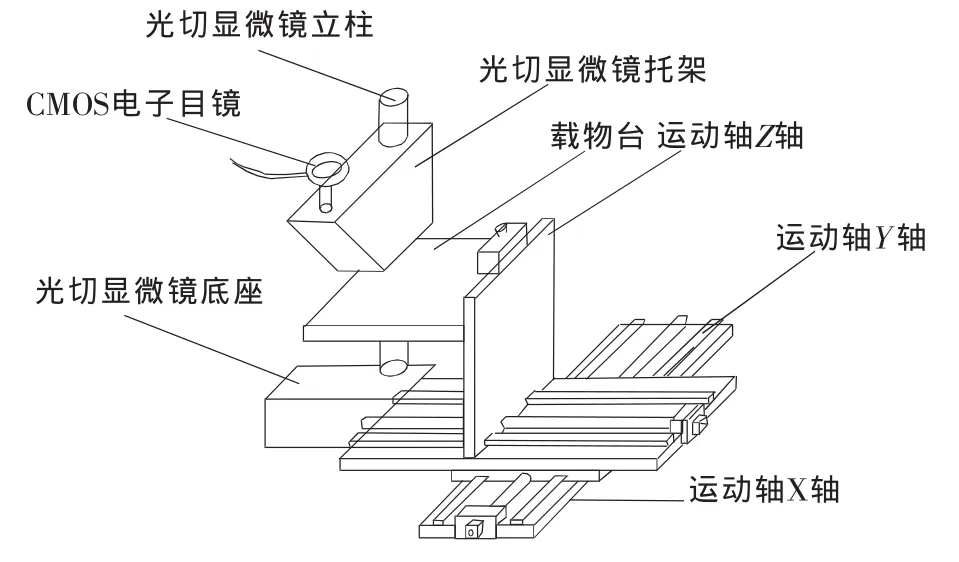
图1 测量系统结构图

图2 利用量块人为制造阶梯差所得影像

4 误差来源与标准不确定度分量分析

4.1 光切显微镜仪器本身误差引入的标准不确定度分量

光切显微镜的机械结构无法达到完美状态，光学镜片的加工也无法保证透镜焦点和镜面曲率的准确，电子目镜成像不可避免的发生扭曲等情况都会影像光切显微镜的示值误差[2]。本测量系统的光切显微镜由普通光切显微镜改造而成，并通过计量机构校准，其示值误差可以参考上海市计量测试技术研究院出具的“微小深度尺寸现场测量系统”检测报告（证书号：2012D33-30-410003）中的检测结果（截取结果部分），如表1所示。

表1 检测结果

仪器示值误差在测量范围内均匀分布[3]，故取均匀分布系数b=0.58，本测量系统7倍镜头测量范围最大为800μm，示值误差为±40μm，14倍镜头测量范围最大为100μm，示值误差为±10μm。由此得到标准不确定度：

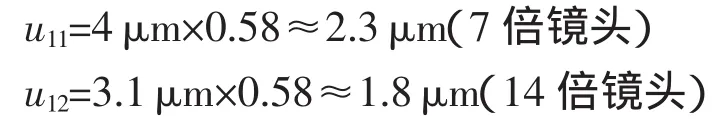
4.2 三轴工作台自动定位引入的标准不确定度分量

本测量系统中的三轴工作台是由伺服电机通过丝杠带动运行，各轴的最小运行间距为0.1μm。在自动定位的过程中仪器无法每次都停留在最佳位置上，对此进行了定位实验。在其他条件不变的情况下采取多次相邻位置测量的方法分析其误差，数据如表2、表3所示。

通过对以上实验数据的观察，可以断定由运动轴定位引起的误差基本呈三角分布[3]，故取均匀分布系数b=0.40。7倍物镜定位实验结果显示临近位置测量结果最大差值为3.48μm，取其半宽度为1.74μm；14倍物镜定位实验结果显示临近位置测量结果最大差值为2.82μm，取其半宽度为1.41μm由此得到标准不确定度：

表2 7倍物镜定位实验结果 单位：μm

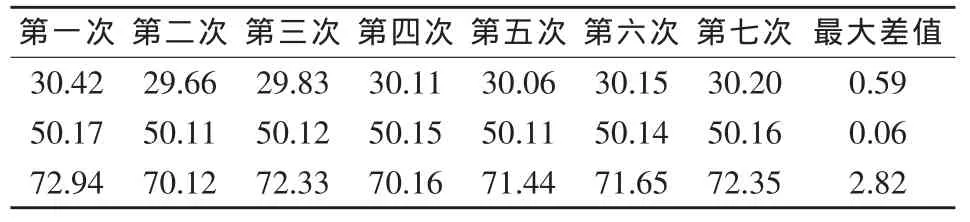
表3 14倍物镜定位实验结果 单位：μm

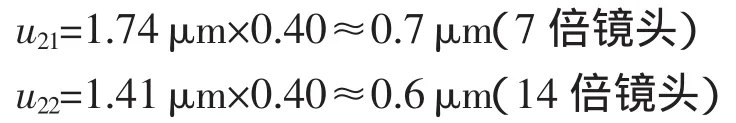
4.3 测量重复性引入的标准不确定度分量

在目前科学理论水平上，无论何种精密仪器都无法完全解析其误差来源，对于这类暂时无法分析但又确实影响测量结果准确性的因素统一归类为随机误差[3]。随机误差带来的标准不确定度通常以重复性实验得到数据，如表4所示，代入贝塞尔公式计算得到。

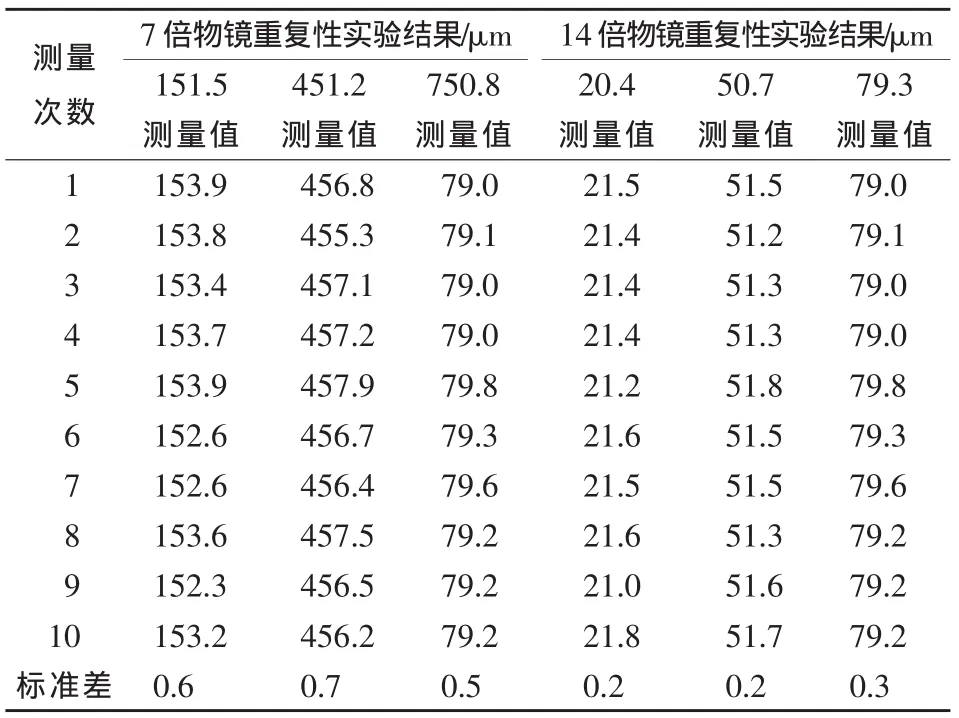
表4 测量10次数据

由此得到标准不确定度：

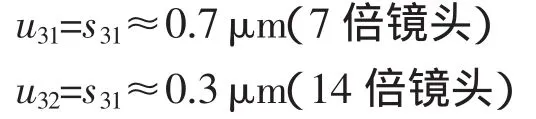
5 各标准不确定度分量相关性分析

由数学模型可知各标准不确定度分量显然不相关。

6 合成标准不确定度

标准不确定度汇总见表5。合成标准不确定度为

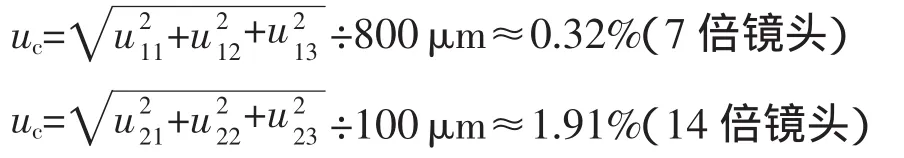
表5 标准不确定度汇总表

7 扩展不确定度

取包含因子k＝2，则扩展不确定度计算结果如下

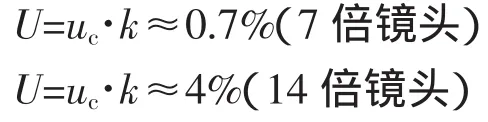
8 结束语

本文对浙江省计量科学研究院开展的“微小深度尺寸现场测量系统的研究”项目中自制的表面深度测量系统在测量微小深度时的误差来源与不确定度进行了分析。通过本次测量不确定度的分析，得到的最终结果符合预期目标，扩展不确定度不大于10%。实验室环境温度为20℃，而将来该测量系统应用到现场测量时温度将偏离20℃，会引入新的系统误差，故本次分析暂未考虑温度变化对测量系统测量精度变化的影响。

[1]施昌彦，宣安东.实用测量不确定度评定及案例[M].北京：中国计量出版社，2003.

[2]JJF 1092—2002光切显微镜校准规范[S].北京：中国计量出版社，2002.

[3]JJF 1059—2012不确定度评定与表示[S].北京：中国质检出版社，2012.

[4]黄柳，余桂英，郑颖君.微小深度尺寸现场测量系统的研究[J].光学技术，2011，37（5）：556-561.