一种新的相位编码信号多普勒补偿算法研究
张宏伟,任新涛,汤宫民,孟 军
(1.军械工程学院雷达教研室,河北 石家庄 050003;2.济南军区72465部队,山东 济南 250022)
0 引 言
伪码调相信号以其低截获概率、高距离和高速度分辨力等优点广泛应用于战场侦察雷达中。然而伪码调相信号的模糊函数成图钉型,对多普勒频率敏感,影响了脉冲压缩后输出的主旁瓣比,因此需要进行多普勒补偿。
在多普勒补偿算法中,应用最多的是多支路补偿算法[1],其使回波信号分别通过各补偿支路,通过比较各支路输出脉压的信噪比来检测目标信息。这种算法对多普勒信息的检测精度低,而且需要多路试探,降低了对目标的捕获效率。基于瞬时自相关的多普勒补偿算法[2],能够很好地消除回波中的多普勒信息,在实际应用中,由于回波延时事先不知道,因此无法确定瞬时的匹配滤波伪码系数。另外,针对正交频分复用信号,可采用零子载波进行非均匀多普勒补偿[3],但这种方法存在信号的发射与处理困难。
本文在研究伪码序列与多普勒容限关系的基础上,提出一种新的多普勒补偿算法。该算法是将回波信号取平方后送到MTD滤波器中,提取回波信号中的多普勒信息,再进行多普勒补偿。
1 伪码序列与多普勒容限的关系
雷达在探测近距离目标时,一般不使用长码,因为长码信号发射的时间比较长,接收时会产生距离盲区;探测远距离目标时,一般不使用短码,因为短码的能量小,自相关主旁瓣比小,会产生距离模糊。对伪码调相准连续波雷达,脉冲压缩等效于对回波信号做非周期自相关接收。巴克码具有很好的非周期自相关性能,但目前找到的巴克码最大位数只有13位[4],不能满足远距离探测雷达的发展需求,下面以常用的M序列码进行分析。
在文献[5]和[6]的基础上,文献[7]中指出,伪码调相信号脉冲压缩输出的主旁瓣比q与多普勒频率fd之间的关系式为
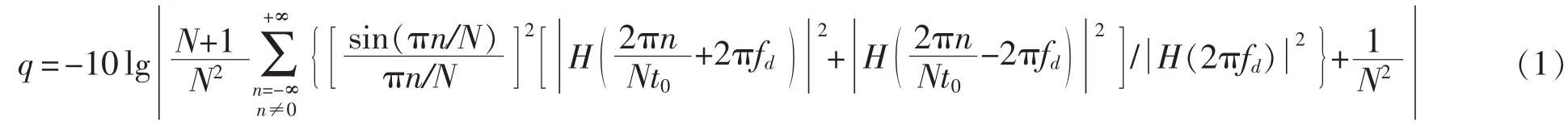
式中:N——调相码的码长;
t0——码元宽度;
H(·)——多普勒滤波器传函。
当H(·)有如图1所示的频域特性时,调相码位数固定,多普勒频率fd增大,脉冲压缩输出的主旁瓣比减小;调相码位数越大,多普勒容限越小,且脉冲压缩输出的主旁瓣比随着多普勒频率的增加下降的越快。
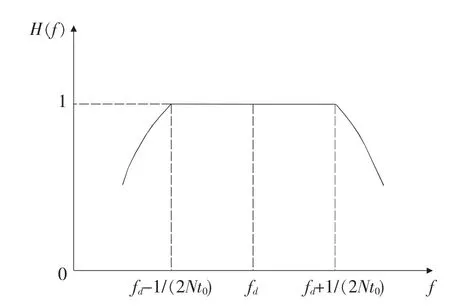
图1 多普勒滤波器的频率特性
若设定伪码调相雷达脉冲压缩后信噪比损失最大可以为3.96dB时,则根据文献[8]记载,在脉冲压缩信噪比损失为3.96dB时,伪码调相雷达所能容忍的最大多普勒频率为
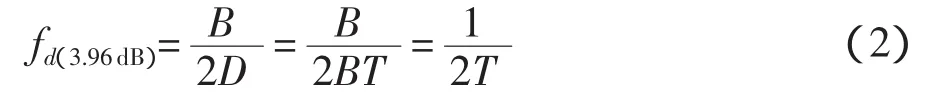
式中:B——发射信号的带宽;
D——发射信号的时宽带宽积;
T=Nτ——发射信号的脉冲宽度;
N——伪码长度;
τ——码元宽度。
例如对发射的1023位M序列码,码元宽度为0.1μs,载频为10GHz,则雷达所能容忍的最大多普勒频率为4887.6Hz,对应的径向速度最大值为263.9km/h,不能满足目前雷达的测速要求,因此必须对回波信号进行多普勒补偿。
2 伪码调相信号多普勒补偿算法研究
伪码调相准连续波雷达回波信号经过数字下变频,将回波信号从中频下变频到视频信号,复数信号表示为
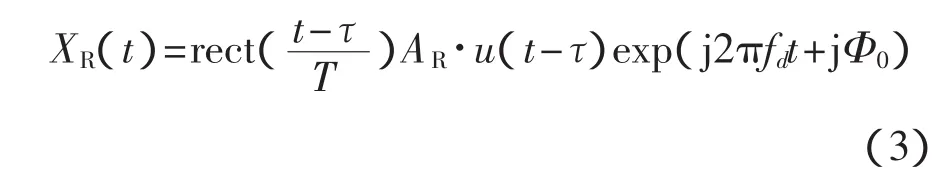
式中:AR——回波信号的幅值;
u(t-τ)——伪码调相信号,取值为±1;
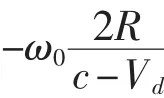
T=Nτ——发射信号的脉冲宽度。
第1步,对回波信号取平方。为获取回波信号中的多普勒频率,对回波信号取平方,滤除回波信号中的伪码调相信号,只留下含多普勒频率的信号。伪码序列u(t)的取值为±1,与自己做乘积得到一组恒为1的常数序列。回波信号取平方即可滤除伪码调相信号,如式(4)所示。
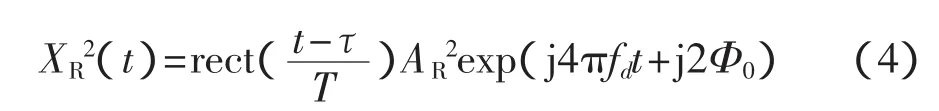
此时回波中多普勒频率的取值增加为原来的两倍。
第2步,将上面处理后的信号通过MTD滤波器组,检测回波中目标的多普勒信息。
若M序列码的长度为127位,码元宽度为0.1μs。当两倍的多普勒频率等于78740.2Hz时,接收到的一个脉冲重复周期内仅含有一个周期的多普勒载频信号,难以准确地检测出回波中的多普勒信息。因此采取多通道MTD滤波器组,对回波中的多普勒频率进行积累检测。设一个脉冲重复周期PRI内的采样点数为n个,对m个脉冲重复周期做MTD处理。可得到如下复数矩阵
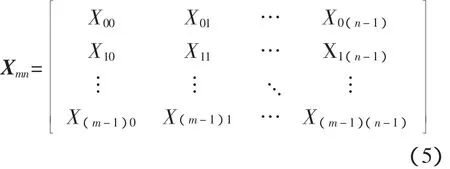
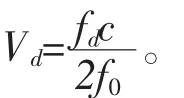
第3步,进行多普勒补偿。有了回波的多普勒频率,则回波的多普勒补偿因子等于 exp(-j2πfdt),将补偿因子与回波信号相乘,可消除多普勒频率fd对伪码信号脉冲压缩输出主旁瓣比的影响。补偿后的信号输出为[9]
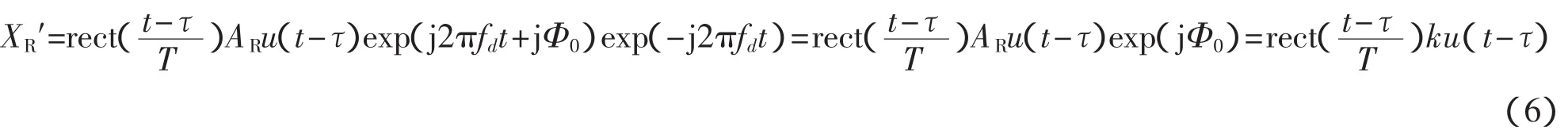
式中:k——常数。
可以看出,补偿后输出信号中不含有多普勒信息。将输出的XR′(t)与发射的伪码反向序列做卷积,即可检测出目标的回波延迟τ,从而可得到目标的距离信息。其算法实现框图如图2所示。
3 仿真分析
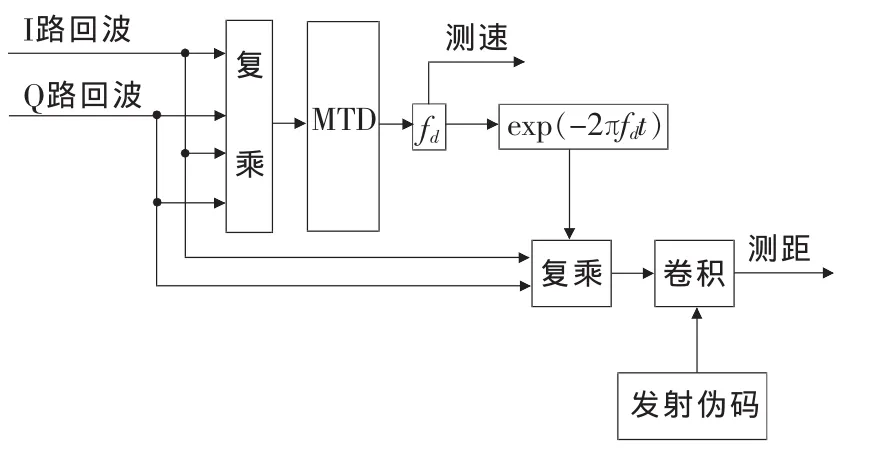
图2 多普勒补偿算法框图
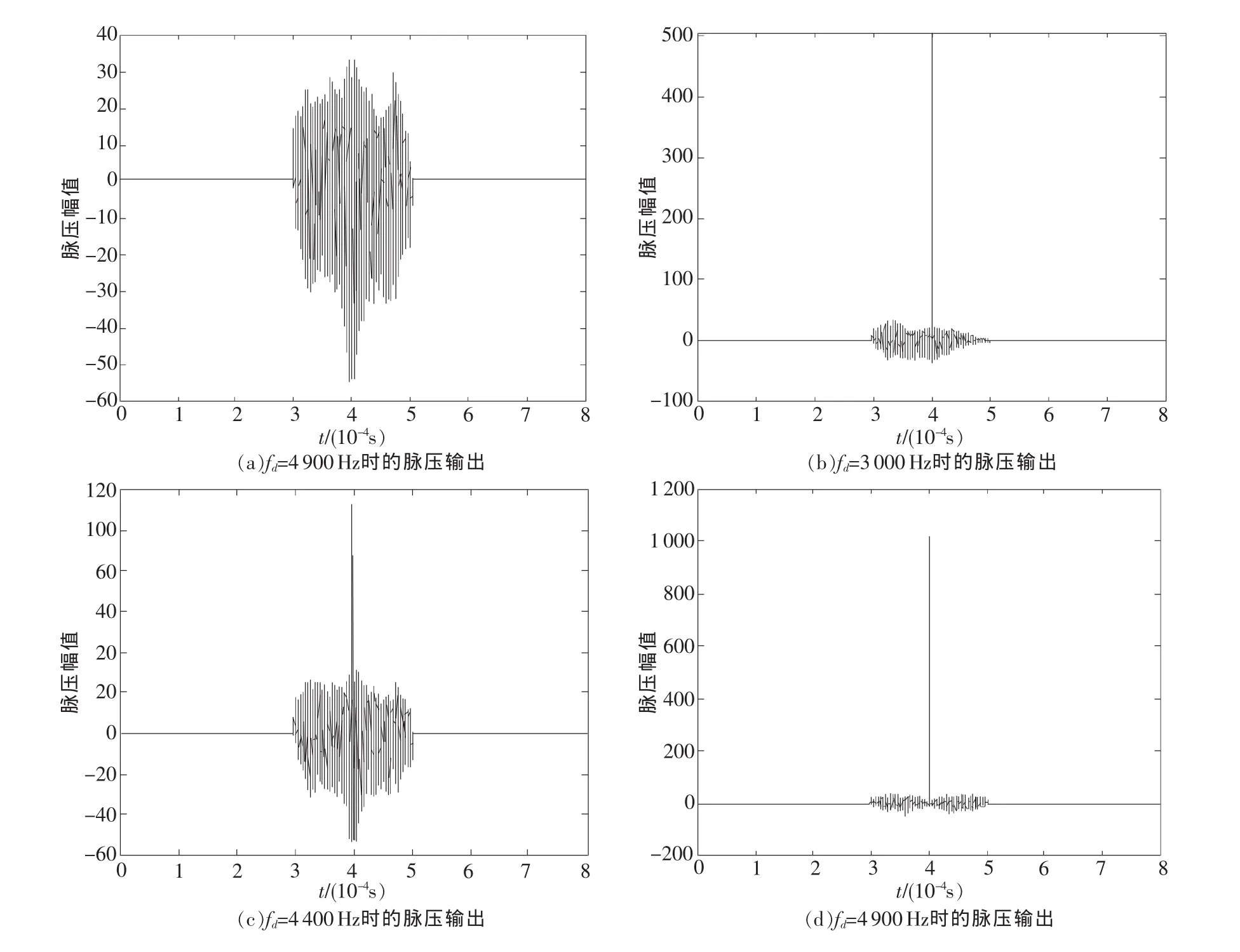
图3 不同多普勒频率下的伪码信号脉压输出
在仿真时,选取的雷达部分参数如下:发射的M序列码位数选取1 023位,码元宽度取0.1μs,载频取10GHz。图3为该雷达在不同多普勒频率下的脉冲压缩输出,及在fd=4900Hz时补偿后的输出结果。可以看出,运动目标的多普勒频率fd越大,脉冲压缩后的主旁瓣比越小。当雷达的多普勒频率大于4 887.5Hz时,脉压后的主瓣被掩埋,从而无法实现对目标的检测。通过多普勒补偿后,能够有效地改善脉冲压缩后输出的主旁瓣比,验证了该算法的可行性。
4 结束语
针对伪码信号在雷达目标检测中存在的多普勒敏感问题,本文提出了一种伪码信号多普勒补偿算法。该算法通过对回波信号取平方,滤除回波中的伪码信息,然后测量其多普勒频率和目标速度,再将求得的多普勒频率转化为补偿因子,与回波信号相乘,抵消回波信号中的多普勒信息,送到脉冲压缩模块中进行测距。该算法通过先测速再测距,能够有效地消除目标多普勒信息对伪码信号脉冲压缩的影响,并能实现伪码调相雷达测速和测距的高分辨性,最后通过仿真达到了预期效果,验证了该方法的可行性。
[1]崔向阳.基于二相编码信号的雷达目标检测及实现[D].西安电子科技大学,2010.
[2]汤礼建,黄建冲,王强.一种基于瞬时自相关的多普勒补偿方法研究[J].空间电子技术,2008(4):89-92.
[3]胡英辉,郑远,耿旭朴,等.相位编码信号的多普勒补偿[J].电子与信息学报,2009,31(11):2596-2599.
[4]李炳新,王志荣,赵晓群.搜索三加权Barker码的穷举算法[J].燕山大学学报,1999,23(4):350-351.
[5]龚济民.伪随机码调相引信[J].兵工学报,1989(4):16-23.
[6]陈金立,顾红,苏卫民.伪码调相连续波雷达的脉压主旁瓣比数学分析[J].兵工学报,2008,29(10):1203-1209.
[7]张庆辉,尹辉.伪码调相引信多普勒容限及其扩展研究[J].弹箭与制导学报,2008,28(5):116-117.
[8]孙晓乐,苏涛.相位编码信号的多普勒频率补偿方法[J].火控雷达技术,2008,37(1):47-51.
[9]Cheng Y P,Bao Z,Zhao P F,et al.Doppler compensation for binary phase-coded waveforms[J].IEEE Transactions on Aerospace and Electronic System,2012,38(3):1068-1072.

