扭转式微小力传感技术研究*

关 涛，刘 铮，郑叶龙，赵美蓉，林玉池

(天津大学精密测试技术及仪器国家重点实验室，天津300072)

近年来，随着航空航天、仪器仪表、生物医药以及微纳制造等各个领域的发展，微小力值(≤10－5N)的计量在各个领域中占据着越来越重要的位置。但是由于受最小标准砝码(1 mg)的制约，目前国内可测量及溯源的，即可计量的最小力值为mN级[1]，大约在10－3N～10－4N。当质量小于 mg级时，质量本身存在很大的不确定度，因此各国并没有建立统一的微小力值的计量方法[2]。

美国、德国、英国、日本、韩国先后构建了微力测量及溯源的体系及装置[3－5]，但由于微小力传感传递机构的灵敏度与稳定性很大程度上决定了微力测量及溯源的成功与否，各国的方案各不相同，且各有利弊，很难同时达到较高的稳定性和灵敏度。

此外，国内近两年也在该领域展开了探索，如弹簧悬挂式、轴承侧卧式静电力发生装置[6－7]，并形成了初步成果，但其测量精度都由于力学传递机构的灵敏度与稳定性缺陷，以及最小标准砝码等限制，难以进一步提高。从国内外对微小力测量与溯源领域的研究来看，微力感应与传递机构是限制微小力测量与溯源精度的主要因素之一，可见微力传递机构是微小力测量与溯源装置成功与否的关键。

以下介绍一种正在探索的基于扭转杠杆原理的微力测量及溯源技术，本文的重点在于对小刚度的微小力传动机构的创新性探索。

1 扭转式微力测量及溯源系统原理及装置

本装置是基于静电力的基本原理来进行的，采用静电力原理复现力值，以静电力平衡杠杆作为微力感应与传递机构，通过SI中的长度量和电学量相结合，进行力值测量与溯源。系统原理示意如图1所示。静电力的产生部分是一个变截面型的圆柱形电容器，该电容器由一组同轴圆柱形电极构成，其中外电极通过组合平移台固定，而内电极可以随杠杆沿竖直方向自由移动，当电压施加于内、外电极时即产生静电力，因此通过控制电容器两极的电压值，以静电力平衡微小力(标准质量)，达到微力测量与溯源的目的。

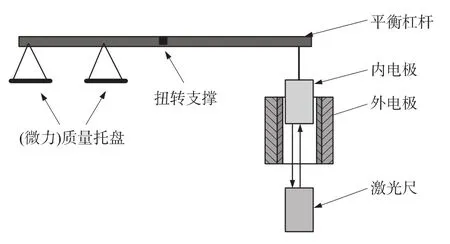
图1 装置原理示意图

如果内外电极同轴，平面内的电容梯度将具有径向对称性，内电极所受合力为竖直方向[8－9]，则静电力与施加控制电压之间的关系由式(1)给出。

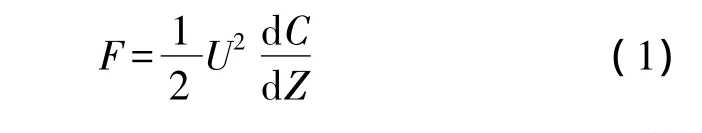
其中，F为静电力(单位为N)，U为内外电极电压差(单位为V)，dC/dZ为电容梯度(单位为 F/m)，即电容随竖直方向位移的变化率。当电容器参数确定后，其电容梯度为定值，因此式(1)中的静电力由电压决定。

电容梯度可由实验获得，在电容器安装调整完成后，利用平移台竖直移动外电级，得到位移量dZ，同时利用电容测量装置测量出电容值的变化量dC，从而得到dC/dZ。

微力测量过程中，通过激光尺测量内电极的位置，确定平衡位置，当施加微力F，杠杆略偏离平衡位置时，通过施加电压U产生静电力，使其平衡微力F，则由平衡时的电压U可以计算得到静电力值，从而获得微力值F。在溯源过程中，通过静电力平衡标准质量产生的重力，可以得出标准质量与电容器电压的关系，达到力溯源到标准质量的目的。

2 力学传递模块分析

微力测量与溯源的最大困难是微小力的传递，力传递系统需要极高的灵敏度以及较快的稳定速度。本装置采用杠杆作为力值传递机构，而杠杆常用的是刀口支撑，如天平等，但是刀口产生的摩擦力矩会带来微小力测量误差。本方案利用弹性材料受力产生微小弹性变形的特性，设计了扭转式支撑，作为杠杆的支点，其具有体积小、无机械摩擦、无间隙、精度高、稳定等性能，适合微位移微小力的传递，Iafolla V等人曾利用此类扭摆测量引力常数G[10]。此外，由于最小砝码(1 mg)仅能提供10－5N的力，为了达到更小的力值传递效果(＜10－5N)，杠杆设计为变臂长结构，但若臂长比过大，则易产生较大的不等臂误差[11]，故选用臂长比为1∶1及2∶1作为初步设计方案。为了在提高灵敏度的同时不影响扭转杠杆的强度，采用重心调节杆来提高杠杆重心，提高其灵敏度。如图2(a)所示，其柔性灵敏部分为中央扭转杆，为提高扭转的均匀性，其有效扭转截面设计为正方形，正方形扭转杆等效力学模型如图2(b)所示。

图2 扭转杆受力模型图

其中L为扭转杆的单边有效长度，a为扭转杆正方形截面的边长;假设支撑座的应变为零，安装时扭转杆没有残余应力，那么在外力矩MT作用下，扭杆扭转的角度可以表示为:

其中G为材料的剪切模量(单位为N/m2)，IT=a4/12为正方形极惯性矩(单位为m4)，在微小位移的情况下，扭转变形可看成是线性的，因此对于横截面为正方形的扭杆，其单边扭转刚度可以表示为:

为了提高扭杆抵抗屈服强度的能力，同时保证具有很好的灵敏度，通常在扭转杆柔性部分和固定端之间加工圆角[12－14]。为了确定固定端对扭转的影响，分别对固定端方式进行Ansys仿真，扭转杆的三种方式的简化模型如图3所示，三种方式的柔性扭转部分尺寸相同，截面为边长1 mm的正方形，长度为20 mm，倒圆角r=1 mm，仅固定端形式不同，并导致倒圆角的个数及状态有所不同，其中(a)为片状固定端，固定端的厚度与柔性部分厚度相同，故仅有两个方向的倒圆角，(b)为方形固定端，厚度大于3 mm，拥有4个方向完整的倒圆角，(c)为薄方形固定端，厚度为2 mm，由于倒圆角r=1 mm，故厚度方向的倒圆角不完整。给3个扭转杆中心加载一个相同的转矩，仿真结果如图4所示。

图3 扭转杆的三种方式示意图

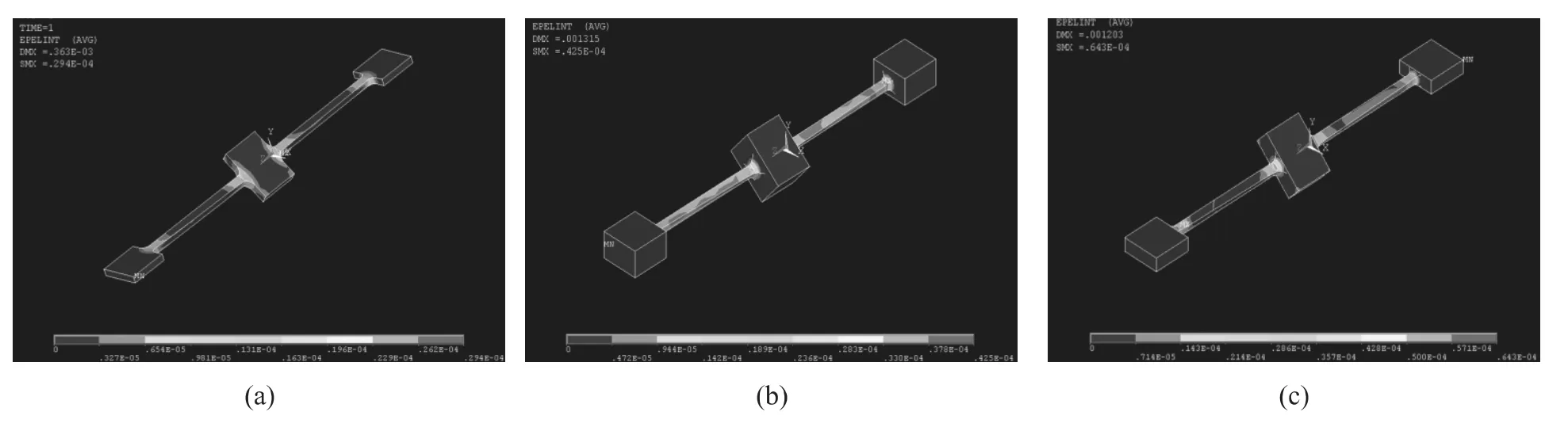
图4 扭转杆的三种方式仿真图

由图4，可以看出，(a)方式的最大位移值D=0.363×10－3mm，最大应力值 S=0．294×10－4N;(b)方式的最大位移量 D=1．315×10－3mm，最大应力值 S=0.425×10－4N;(c)方式的最大位移值 D=1．203×10－3mm，最大应力值 S=0．643×10－4N。可见，后面两种方案有较好的灵敏度，然而，采用不完整的倒圆角会带来局部应力的提升，为了使扭转杆具有较好的强度，并同时具有较好的灵敏度，选用方案(b)作为实验装置。

图5为简化的扭杆示意图，由此可以计算得到扭转杆绕 x 轴[15－17]的扭转刚度为

其中a=0．333，b=0．21均为常系数，L为有效扭转长度，r为倒圆角半径，t、w分别为扭转杆矩形截面的长与宽，由于采用了正方形截面则w=t。

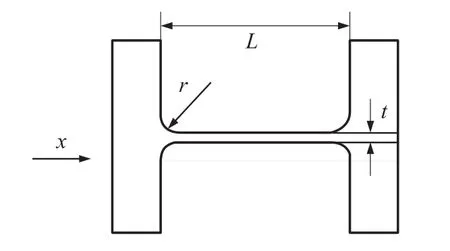
图5 扭杆示意图

扭转杆采用的铍青铜板状材料(QBe2．0)，其具有高硬度、高弹性、无磁性等特点，适于制造精密柔性结构。它的主要物理特性和机械性能有:杨氏模量 E=1．3×1011N/m2，剪切模量 G=5．0×1010N/m2，泊松比 ν=0．33，密度 ρ=8260 kg/m3，热膨胀系数为1．78×10－5/℃，热时效处理前的拉伸强度为 σs=637×106Pa，热时效处理(温度300℃，时间1．5 h)后的拉伸强度为 σs=1176×106Pa。

由式4可知，扭杆的刚度主要决定因素是其柔性部分的截面边长t，其对应关系如图6所示，近似为4次方关系。由以上分析，可以计算出截面边长t为1 mm，单边有效扭转长度L为20 mm，倒圆角半径r=1 mm时，单边扭转杆的扭转刚度的理论值为0．3 N/rad。双边扭转杆模型相当于弹簧并联，两边的扭转变形相同，产生相同的扭力，扭力叠加值平衡外来的扭矩，故此双边扭转杆的理论刚度为0．6 N/rad。所以当加100 mm的杠杆(单边力臂)时，理论灵敏度可达6 N/m。由于激光尺的分辨力约为10 nm，故此微力系统的理论分辨力可达6×10－8N。实验装置如图7所示。

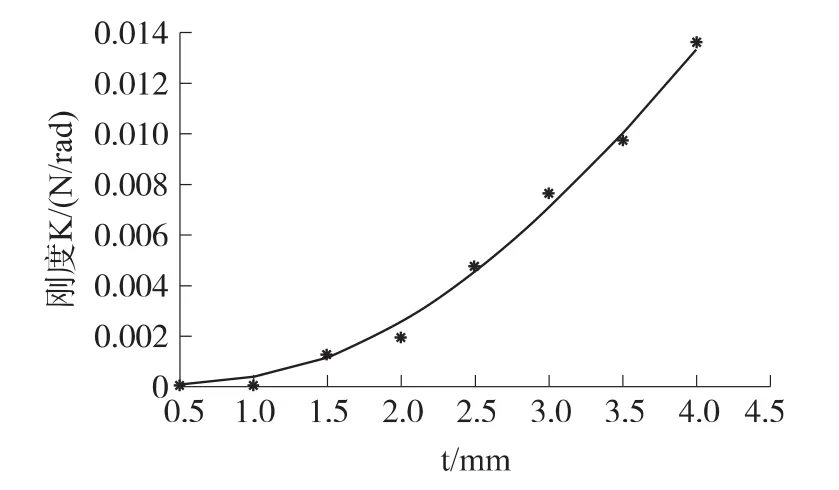
图6 扭杆刚度与截面边长的关系

图7 实验装置实物图

3 实验结果及误差分析:

为了采用现有装置测量扭转杆刚度，采用激光尺测量杠杆受力后的位移值，从而计算出扭转杠杆的实际刚度与灵敏度。实验选用1∶1杠杆，杠杆臂总长200 mm，扭转杆截面边长1 mm，选取不同标称的标准质量(E2级)加载于杠杆托盘，并使用激光尺测量杠杆(内电极)位移值，实验结果如图8所示。

由图8可见，扭转杆截面边长为1 mm时，扭转杠杆的刚度约为10 N/m，且质量与位移之间有较好的线性对应关系，线性度不低于98%，能够满足测量与溯源的要求。以下分析本装置及方法的误差来源及改进方向。

图8 采用截面边长为1 mm扭转杆的刚度测量结果

扭转式静电力测量的误差来源于多个方面，其中误差主要来源于:内外电极偏离同轴、电源电压的精度、标准砝码的精度、各尺寸加工精度、扭杆弯曲变形、杠杆变形、环境振动等。下面主要分析传动机构带来的误差，即扭杆弯曲变形及杠杆变形。

已知扭杆的形变是弯曲和扭转的组合形变，则在加载外力(或质量)时，激光尺测出的位移为弯曲和扭转放大的位移合。当单边扭杆的长度为L时，双边梁产生的最大弯曲挠度为[18]:

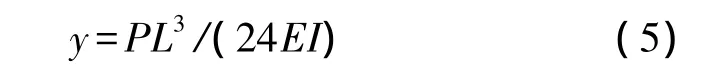
其中，P为扭杆受到的力，L为扭杆长度，E为材料的杨氏模量，I为极惯性矩。激光尺分辨力为10 nm，现在取扭杆截面为边长为1 mm的正方形，长L=20 mm，位移 y=10 nm，此时加载的力值 P=3．2×10－4N，即当测量的力值大于10－4N时，扭杆产生的弯曲变形已经较大的影响其扭转测量效果。但在力值较小的范围时，由公式(2)和式(5)，可得扭转变形和弯曲变形的比值:

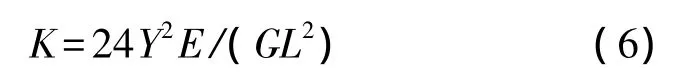
其中，Y为杠杆臂长，L为扭杆长度，E为材料弹性模量，G为材料剪切模量。若扔选用铍青铜为扭转杆材料，则K=62Y2/L2，即相对误差取决与杠杆臂长Y与扭杆长度L的比值，实验中选用L=20 mm，Y=100 mm，则K=1 550，即弯曲误差对测量精度的影响小于1‰。

除此以外，在加载外力时，杠杆臂也会产生一定的弯曲变形，由材料力学，单边梁产生的最大弯曲挠度为:

假设，杠杆截面为边长为10 mm的正方形，长L为100 mm，载荷取10－4N，杠杆材料选择绝缘的非金属塑料，取E=0．1×1011N/m2，可以得出此时的杠杆的弯曲值 y=4×10－9m=4 nm，且由式，4、5，此时扭转杠杆的扭转变形量为1．7×10－5m，扭转杆的弯曲变形量为6．2 nm。可见此时杠杆与扭转杆的变形已经能够被激光尺检测到，其对测量结果的误差影响约为6‰，且随着被测力的减小，其对系统测量结果影响逐步减小。

4 结论

本文介绍了一种正在探索的基于扭转式杠杆原理的新型微力测量及溯源技术，并深入探讨了扭转式微力传感机构的特点，分析了微小力传递机构对整体测量的影响，从材料力学出发，利用有限元分析得出了倒圆角与固定端的形式对扭转杆的应力与灵敏度的有较大影响，结合扭转刚度公式，分析了扭转杠杆的各项参数对其分辨力的影响，同时推倒得出扭杆的扭转弯曲比，及其对系统测量误差的影响。在此基础上，搭建了基于扭转式杠杆的微小力测量平台，并进行了理论验证实验。实验结果表明，扭转式杠杆具有较高的力学分辨力，能够满足微小力(≤10－5N)的测量与溯源，为后续的进一步研究提供了理论和实验的基础依据。

[1]张军，李寒光，李映君，等．压电式轴上六维力传感器的研制[J]．仪器仪表学报，2010，31(1):73－77．

[2]Jabbour Z L，Yaniv S L．The Kilogram and the Measurements of Mass and Force[J]．Res Nat Inst Stand Technol，2001(106):25－46．

[3]Jon R Pratt，John A Kramar．SI Realization of Small Forces Using an Electrostatic Force Balance[R]．ⅩⅧ Imeko World congress Metrology for a Sustainable Development．2006，9:17－22．

[4]Yusaku Fujii．Method of Generating and Measuring Static Small Force Using Down-Slope Component of Gravity[J]．Review of Scientific Instruments，2007，78(6):1－3．

[5]Vladimir Nesterov．Facility and Methods for the Measurement of Micro and Nano Forces in the Range below 10－5N with a Resolution of 10－12N(Development Concept)[J]．Measurement Science and Technology，2007，18:360－366．

[6]王海涛，林玉池，付鲁华，等．微小力值传感系统的实验研究[J]．传感器与微系统，2009(8):8－11．

[7]盛阳，赵美蓉，刘明，等．超微力发生系统及其电容采集模块的设计[J]．传感技术学报，2010，23(10):1505－1509．

[8]祝卫堃．电轴法在静电场中的应用[J]．物理与工程，2007(6):11－12．

[9]刘明，林玉池，郑叶龙，等．利用静电场原理复现微小力值的实验研究[J]．传感技术学报，2012，25(1):33－36．

[10]Iafolla V，Nozzoli S，Fiorenza E．One Axis Gravity Gradiometer for the Measurement of Newton’s Gravitational Constant[J]．Physics Letters A，2003(318):223－233．

[11]王鹏．变臂比杠杆式精密力源技术的研究[D]．吉林:吉林大学，2009，5:14－21．

[12]Feng-Zone Hsiao，Tai-Wu Lin．Analysis of a Novel Flexure Hinge with Three Degrees of Freedom[J]．Rev Sci Instrum，2001(72):1665－1573．

[13]Chang-Soo Han，Soo-Hyun Kim．Three-Axis Lever Actuator with Flexure Hinges for an Optical Disk System[J]．Review of Scientific Instruments，2002(73):3678－3686．

[14]Yakov M．Tseytlin，Notch Flexure Hinges:An Effective Theory[J]．Review of Scientific Instruments，2002(73):3363－3368．

[15]Nicolae Lobontiu，Ephrahim Garcia，Steven Canfield．Torsional Stiffness of Several Variable Rectangular Cross-Section Flexure Hinges for Macro-Scale and MEMS Application[J]．Smart Materials and Structures，2004(13):12－19．

[16]Nicolae Lobontiu，Ephrahim Garcia．Stiffness Characterization of Corner-Filleted Flexure Hinges[J]．Review of Scientific Instruments，2004(75):4896－4905．

[17]Tino Noll．Three Axis Rotational Flexure Joints of High Axial Stiffess[J]．Precision Engineering，2002(26):460－465．

[18]董景新，吴晓春，高钟毓．一种扭摆式加速度计的结构[J]．清华大学学报，2000(40):81－84．