基于FFT-Matching Pursuit的心电身份识别算法研究*

赵治栋，杨 雷，陈甸甸

(1．杭州电子科技大学电子信息学院，杭州310018;2．杭州电子科技大学通信工程学院，杭州310018)

与传统的基于密码或ID卡的认证方式相比，生物识别技术(Biometrics)具有更高的安全度与可靠度，已逐渐成为国际研究的热点，并逐渐在不同的领域发挥着举足轻重的作用。生物识别的优势在于更高的安全性和便利，但在实际应用中也面临许多挑战，其中比较突出的是安全问题[1]。有人成功利用明胶制成的假手指骗过了指纹识别系统[2];利用打印下的虹膜图片或者在隐形眼镜上蚀刻出的虚假虹膜，可以让虹膜识别系统真假难辨[3]。生物特征识别应用过程中所潜藏的安全问题引起了国内外研究者的格外重视，新的生物特征识别技术不断涌现[4－5]。

近年来出借助于人体内蕴的心电信号ECG(E-lectrocardiogram)进行身份识别的方法广受关注。相比传统的生物识别技术，心电识别技术具有独特的优势:首先，心电来自于人的心脏，不易被轻易仿制，与指纹和人脸等比，具备高安全性;其次，任何人都有心电，具备普适性;第三，心电信号因人而异，不同的心脏位置、尺寸、解剖结构和胸腔结构等造成了心电信号的差异;第四，心电信号是一维信号，处理简单，数据量小，节省存储空间;第五，心电信号可以通过手指电极方便的数字化采集;最后，心电信号具有较长期的稳定性。国内外对心电身份识别做了初步的探索研究。从研究方法上分，目前ECG身份识别算法大致分为三种:基于多基点检测的特征提取方法、基于单基点的特征提取方法和非基点检测的特征提取方法。本文重点研究非基点检测的身份识别算法。Biel早期详细研究了利用ECG信号作为身份识别的可行性[6]。Wang从心电信号中提取了解析特征和外观特征相融合的特征，并利用PCA对13个心电信号进行分析，获得100%的个体识别率和98．9%的心跳识别率[7]。Ming Li提出了一个融合时域和复倒谱信息的识别方法，识别率可达98．3%[8]。杨向林等人根据R波位置以固定长度提取单个心跳周期的心电信号，并对其进行小波分解提取小波参数，最后选用相关系数阈值法实现身份识别;基于波形特征、小波特征和融合特征的识别率分别达到82．5%、87．5%和 95%[9]。Platanioatis提出了自相关系数(AC)结合离散余弦变换(DCT)的非基点检测识别方法，采用高斯似然距离获得100%的识别率，采用欧式距离获得92．8%的识别率[10]。

本文研究了基于快速傅里叶FFT(Fast Fourier Transform)的匹配追踪MP(Matching Pursuit)心电身份识别算法。通过心电信号的预处理:消噪和标准化，提高了心电信号消噪比，消除了心率变异;通过分析MP过完备原子库的结构特性和心电信号的特征，提取前三个原子的时频参数和投影值作为特征参数，然后构建支持向量机SVM(Support Vector Machine)进行分类匹配，完成识别;最后通过MIT-BIH心电数据库验证了算法性能，取得了较高的识别率。

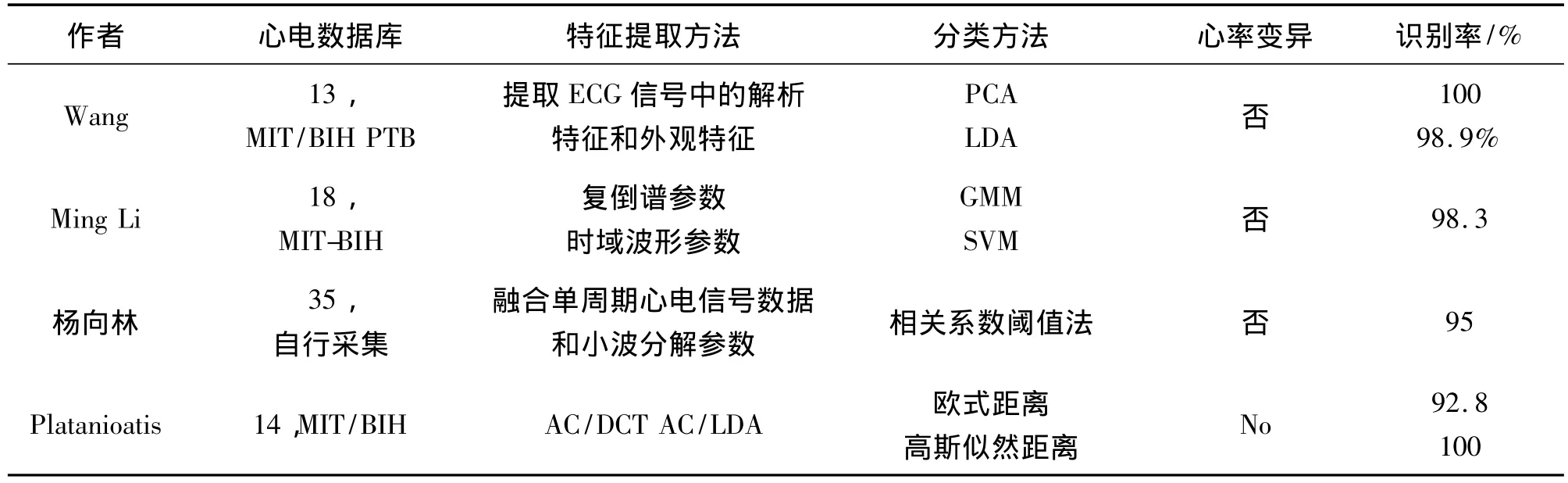
表1 各种典型心电身份识别技术的比较

1 基于FFT-MP的信号稀疏分解

MP算法是常用的信号稀疏分解方法之一，通过不断的迭代来求取待分析信号的稀疏表示，是一种贪婪算法。

用于MP稀疏分解的过完备原子库可表示为D={gγ}γ∈Γ，gγ表示过完备库中的原子，它的长度与待分析信号长度相等，它由时频参数γ确定，库内原子都作了归一化处理，即‖gγ‖=1。假设H表示Hilbert空间，原始的待分析信号f∈H，则MP算法的基本流程如下所述[11]:

初始化:使得R0=f。首先从过完备原子库中找出满足式(1)，最能匹配待分析信号结构特征的原子 gγ0。

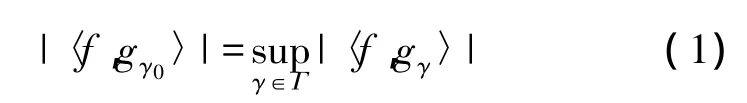
然后将待分析信号分解为如下形式:

式中〈f，gγ0〉gγ0表示待分析信号 f在原子 gγ0上的投影，R1f为待分析信号在原子gγ0上投影后的剩余分量。待分析信号经过一次分解后，得到在最佳原子gγ0上的投影和及其剩余分量R1f两部分。显然，R1f与原子gγ0是正交的。

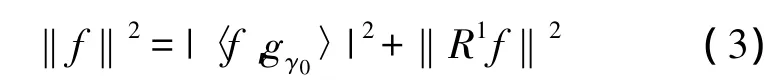
为了使剩余分量的能量‖R1f‖2最小化，必须选择合适的原子 gγ0最大化 |〈f，gγ0〉|2。但是由于计算量等因素的限制，原子的选择受到一定的限制，因此只能选取满足下列条件的最佳逼近原子gγ0。

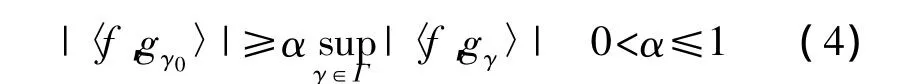
式中α表示最优因子，通常α=1。MP是一个不断迭代的过程，通过重复上面同样的分解过程，将信号剩余分量Rkf在其最佳匹配原子gγk上投影得到下一阶的剩余分量，从而不断地对其进行分解。当‖Rkf‖足够小时，上述分解过程即停止。信号被分解为:

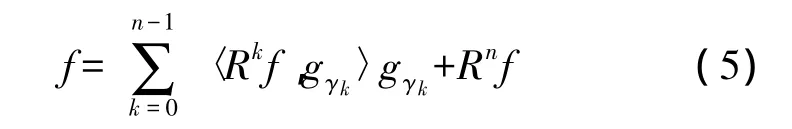
其能量表示形式如下:

式中Rnf表示待分析信号经过n次分解以后得到的剩余分量。已经证明在信号长度有限的条件下，随着n的增大剩余分量的能量‖Rnf‖逐步衰减为零[11]。用较少的原子可以表示原始信号的主要成分，从而待分析信号可以近似地表示为:

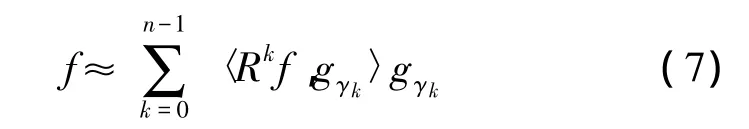
其中n≪N，N表示待分析信号的长度。

根据心电信号的时频结构，本文中选择由Gabor原子来形成过完备原子库。一个Gabor原子可由一个经过调制的高斯窗函数组成[12]:

其中g(t)=e－πt2表示一个高斯窗函数，时频参数γ可表示为 γ=(s，u，v，w)，s为尺度因子，u 为位移因子，v为频率因子，w为相位因子。由过完备原子库的结构特性可知时频参数γ=(s，u，v，w)可决定一个原子。当参数s，v，w相同而只有参数u不同时，原子的形状是相同的，只有中心位置不同。本文预处理后得到的心电模板各段的位置基本保持稳定，因此可省略这些原子从而减小原子库中原子的数目。根据上面的分析，可使参数u的值保持不变，其他参数s，v，w按照原来的方法进行选取，过完备原子库中的原子数目将大大减小，有效提高算法的计算速度。可将N次内积运算转换为一次Rkf和gγ的互相关运算，以提高计算效率。

FFT可快速实现互相关运算，在每次分解过程中找到与心电信号或心电信号剩余分量匹配性最好的原子，大大地提高了MP稀疏分解的运算速度，且不会影响心电信号的稀疏表示。

2 FFT-MP心电特征提取算法

该算法主要包括3个部分:预处理、特征提取和分类。首先对心电信号做消噪和标准化等预处理，然后将得到的心电模板进行FFT-MP分解得到原子的时频参数和投影值，将其作为特征参数输入到SVM分类器中进行训练，最后利用ECG数据进行性能测试。算法的主要流程图如图1所示。

2．1 心电预处理

实际采集到的心电信号会受到外界噪声等因素的干扰，污染了心电信号的波形，严重影响了身份识别的准确度。本文提出了心电信号预处理算法，算法的具体流程如图2所示。

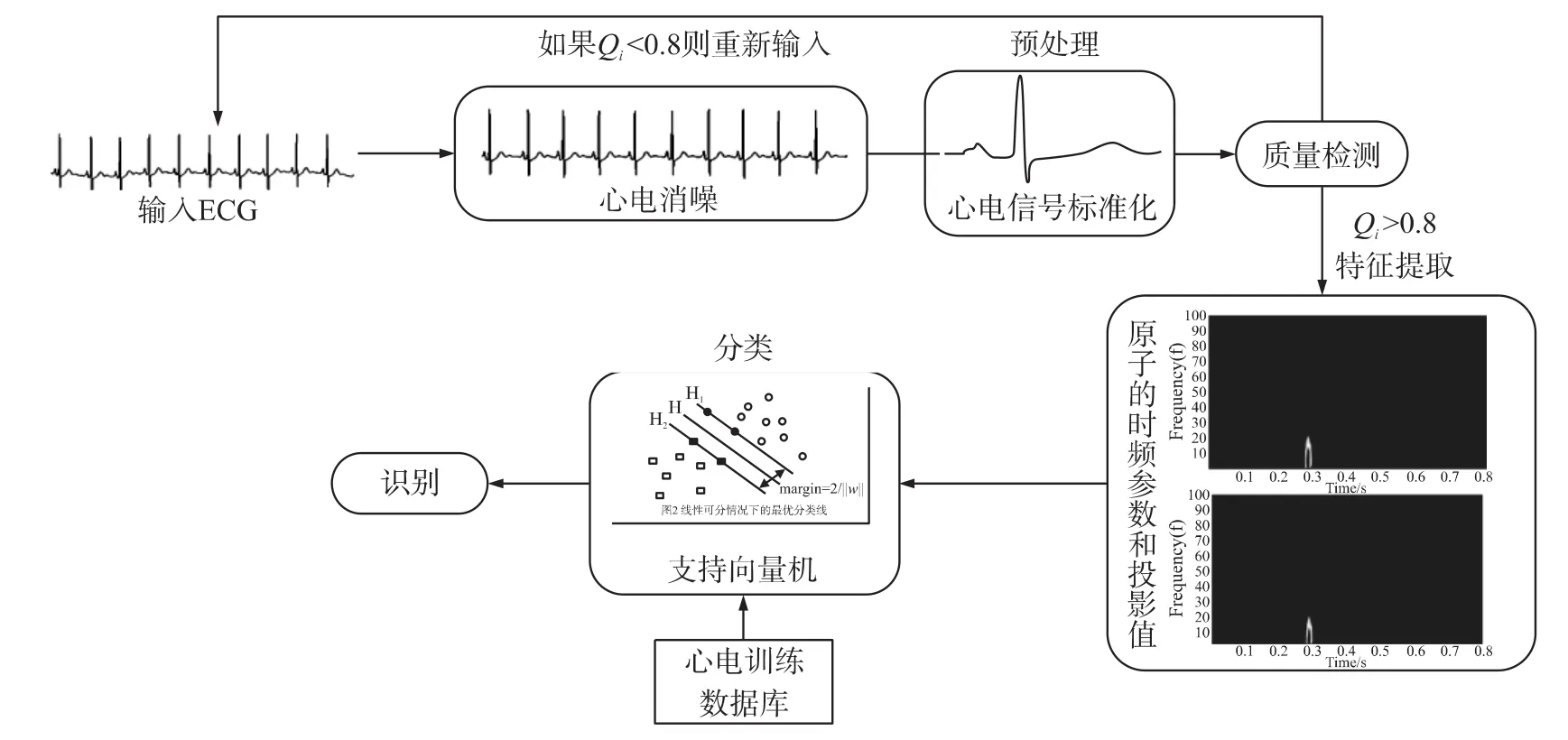
图1 FFT-MP心电特征提取算法流程图

图2 预处理过程的流程图

(1)心电信号消噪:首先采用平滑先验法对心电信号进行处理，消除心电信号中基线漂移等低频噪声，然后采用基于小波阈值的去噪方法消除心电信号滤除中高频噪声。平滑先验法可有效滤除基线漂移和其他低频噪声，可以通过参数λ来调节该滤波器的截止频率[13]。经过平滑处理后的心电信号通过Sym4小波对其进行三层小波分解，然后对分解得到的小波系数采用极大极小阈值和软阈值函数进行去噪处理[14]。经过心电消噪处理前后的心电信号如图3所示。

(2)心电信号标准化:在每次心电信号采集过程中，受测者的心率一般会随着受测者的情绪、压力状态等而改变，心率的改变对心电身份识别造成一定的影响。本文提出了心电信号标准化方法以消除此影响，流程图如图4所示。

为了得到标准化的心电信号，首先从输入的心电信号S中提取出每个心跳周期的心电信号M(i)。本文采用基于双正交样条小波的QRS波检测方法来检测心电信号的R波[15]，R波的位置可以表示为p(i)，i=1，2，3，…，m。

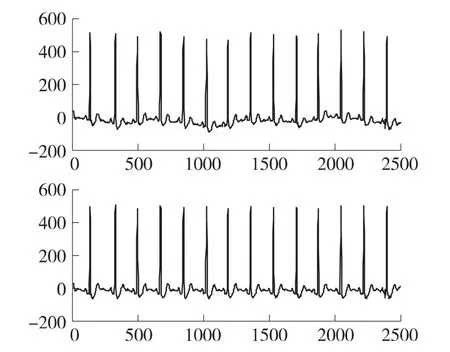
图3 去噪前后心电信号

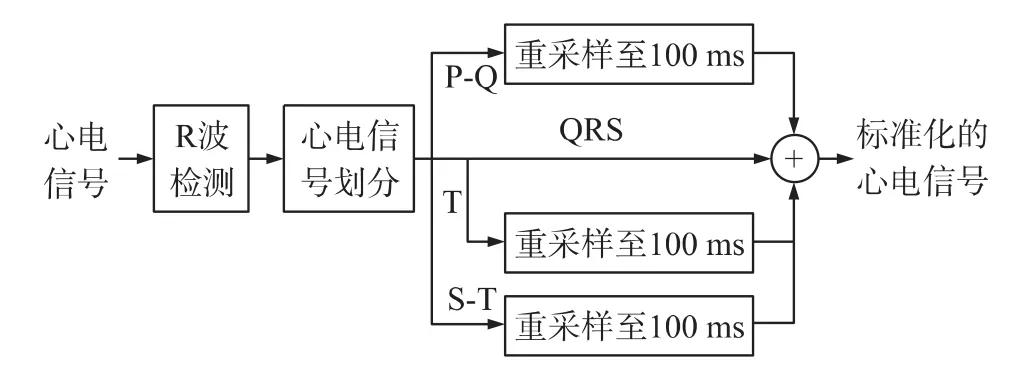
图4 心电信号标准化流程图

在确定心电信号R波的位置后，根据波形的特点，将单个心跳周期的心电信号划分成4个部分:PQ间期、QRS复合波、S－T间期和T波，如图5所示。

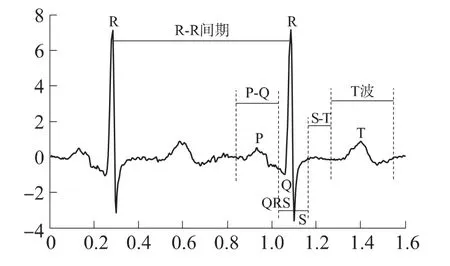
图5 典型的心电信号波形

QRS复合波在心率改变的情况下基本保持稳定，因此取 R 波前(0．06×fs)个采样点，R 波后(0．1×fs)个采样点作为单个心跳周期心电信号的QRS复合波，表达式如下:

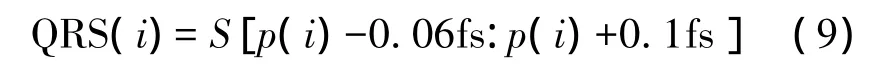
其中fs表示心电信号的采样频率。

P－Q间期波形会随着心率的改变而轻微的发生变化，它的标准化可通过下式获得。

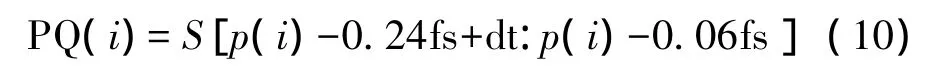
其中dt是一个阈值变量，由心率决定，它可以表示为:

T波波形随着心率的改变变化比较显著[17]，因此把T波分成两段，一段从 S波结束点 s(i)=S[p(i)+0．1fs]开始到 T波开始点称为 S－T间期，另一段从T波开始点到结束点，称之为T波。这两段间期可以表示成:

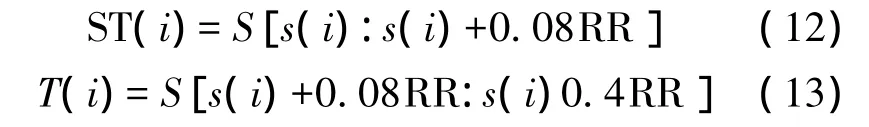
在单个心跳周期的心电信号中P－Q间期，S－T间期和T波会随着心率的改变而改变，根据式(9)、式(10)、式(12)和式(13)可以得到相对应的P－Q间期，S－T间期和T波，然后分别将P－Q间期重采样至216ms，S－T间期重采样至100 ms，T波重采样至320 ms，这些间期都是心率为75 bpm时的长度。在重采样之后，将这四个间期重新组合起来，组成一个完整心跳周期的心电信号波形，时间长度为800 ms。在心电信号采集过程中心电信号的幅度也会受到受测者心理状态、周围环境等因素的影响，因此需要对心电信号的幅度进行相应的归一化处理。

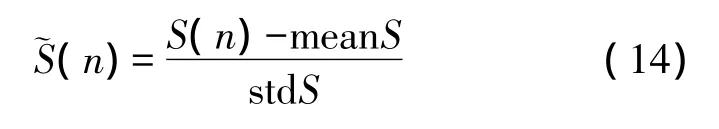
根据式(14)可以得到零均值单位方差的归一化信号。标准化后的心电信号如图6所示，有效的去除了心率变异性的影响。

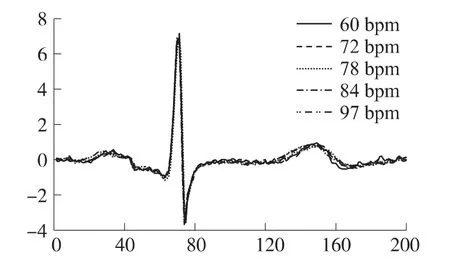
图6 标准化后的心电信号

(3)心电信号质量检测:心电信号在经过消噪和标准化后，需要判断心电信号是否满足识别所需的质量要求。根据心电信号的准周期特性及周期变换的特点[18]，提出了基于周期变换的检测方法来判断心电信号的质量。

将经过心电信号标准化的单个心跳周期的心电信号Si重新拼接起来组成一个合成信号，可以表示成 F=[S1，S2，…，Sn]。因为合成信号可作为一个准周期信号，噪声会造成信号波形的改变从而影响信号的周期性。可通过周期变换将合成信号投影成一系列的周期序列，检查合成信号的周期性。经过周期变换后，根据式(15)来估计质量评价参数Qi，Qi表示合成信号的周期性，即合成信号受到噪声或其他因素影响的程度。

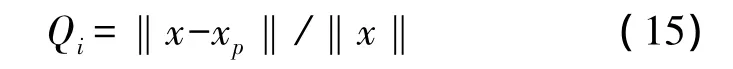
x是原始序列，xp是投影到周期子空间p的周期序列。Qi计算原始序列与投影后的周期序列之间的相对能量，表示原始序列与周期序列之间周期的接近程度。Qi越大表示合成信号受到噪声和心率变化影响较小，反之说明受到干扰较大。经过大量实验，设定阈值为0．8，当合成信号的Qi大于0．8时，则表示心电信号质量满足识别要求;当Qi小于0．8时，则提示重新输入另一段新的心电信号。

2．2 基于FFT-MP的心电特征提取

由于同一个人的心电模板信号有着相似的波形，因此同一个人的心电模板信号经过MP稀疏分解后得到的原子的时频参数有着最大的相似度。原子是由时频参数 γ=(s，u，v，w)决定的，同一个人的时频参数有着最大的相似度，因此稀疏分解得到的时频参数可以作为心电信号的特征参数。

此外，待分析的心电模板信号或剩余分量与最佳原子的匹配度可用其在最佳原子上的投影值大小来表示，投影值越大，表示该原子在原始心电模板信号或其残余分量中所占的比例越大。原子的投影值也可以作为特征参数。同时最先分解得到的原子投影值较大，在选取特征参数时可以仅选取前几个原子的时频参数和其投影值。图7是采用FFT-MP稀疏分解算法得到的心电模板信号的时频分布图，其中图中央是心电模板信号的时频分布，底部是信号的时域分布，右侧是信号的功率谱，从图中可知通过原子重建得到的时频分布图较好反映了原始信号的时频特性。

图8为同一个人不同时间段的心电模板信号稀疏分解后的时频分布图，图9为四个人的心电模板信号稀疏分解后的时频分布图。从图8、图9中可以看到同一个人的原子的时频图有着相似的时频分布，而不同人的原子的时频图各不相同，因此可知原子的时频参数具有较好的区分特征和稳定性。

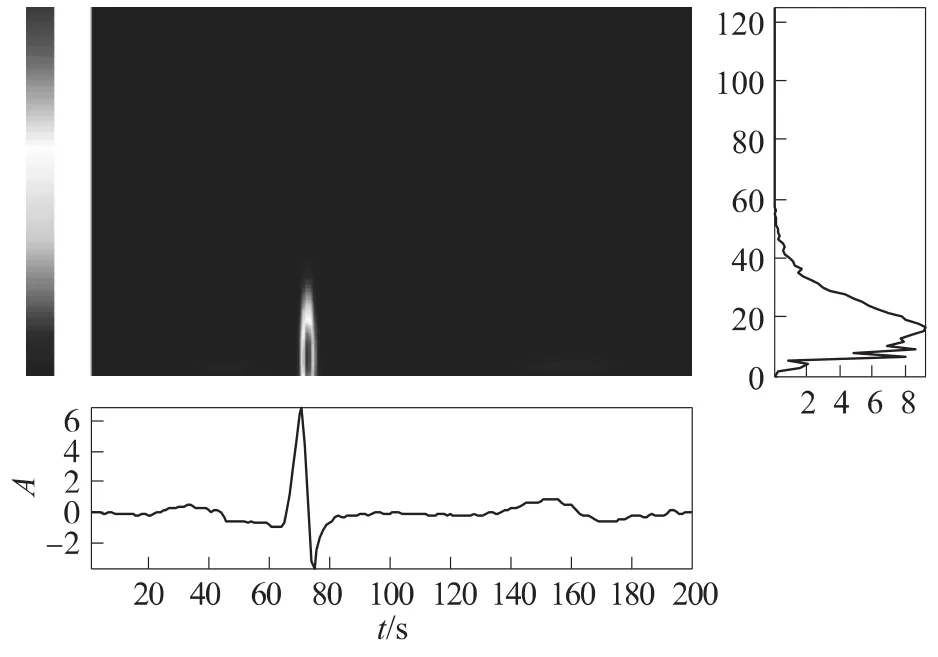
图7 FFT-MP稀疏分解算法得到的心电模板信号的时频分布

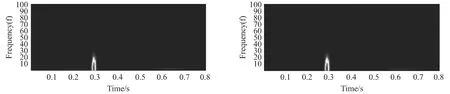
图8 同一个人不同时间段的心电模板信号稀疏分解后的时频分布

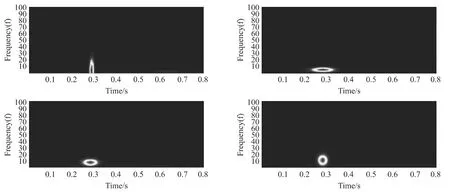
图9 四个人的心电模板信号稀疏分解后的时频分布

2．3 SVM分类器

支持向量机是建立在Vapnik和Chervonenkis(VC)理论和结构风险最小原理的基础上，在线性可分的情况下求最优超平面，最优超平面不仅能将两个类别的样本正确分开，使得经验风险最小，而且两类样本之间的距离最大，非常适用于小样本情况下的分类和识别[19]。支持向量机示意图如图 10所示。

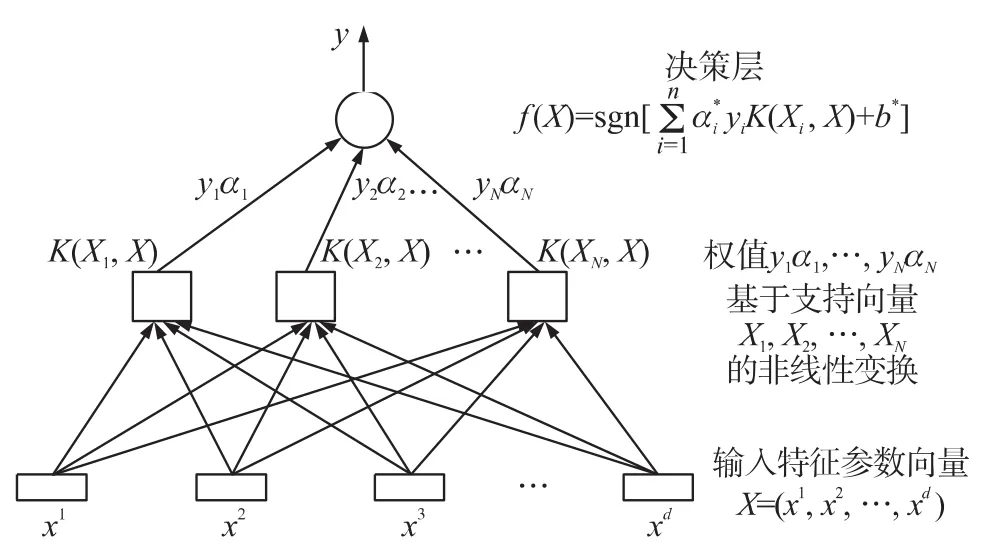
图10 支持向量机示意图

将前n个原子的时频参数和投影值作为心电模板的特征参数输入到SVM分类器中进行身份识别。软件采用LIBSVM。

3 实验结果与讨论

在本节中讨论参数选取对识别率的影响。训练选取20 s的心电数据，测试选取10 s的心电数据，最后的识别效果通过单个心跳周期的心跳识别率和10 s测试数据中提取的前三个心电模板的判别结果通过多数投票准则得到的识别率来进行衡量。

在训练过程中，选取心率范围在50 bpm～80 bpm的20 s心电信号，对其预处理，提取出单个心跳周期的心电模板，进行质量检测，若检测出的Qi不满足阈值条件，则重新输入心电信号，直到Qi满足要求为止。对心电模板进行FFT-MP稀疏分解，将得到的前三个原子中的时频参数以及投影值作为特征参数，即每个心电模板可获得一个1×12的特征矢量。最后将提取出的特征参数保存到模板库中，采用交叉验证法训练模板库，得到SVM的最优参数，构建SVM分类器。

在测试过程中，首先对输入10 s的测试心电信号进行预处理，采用FFT-MP提取特征参数，最后输入到SVM分类器中与训练模板库中的特征进行匹配分类，根据多数投票准则得到判别结果，最后根据心跳识别率和识别率来评价算法性能。

3．1 ECG 数据

选取MIT-BIH的3个心电数据库:ST change数据库，Long Term ST数据库和QT数据库中的心电作为实验数据[20]。ST change和Long-Term ST数据库选取的同一个人心电数据中存在心率变异，如图11所示。

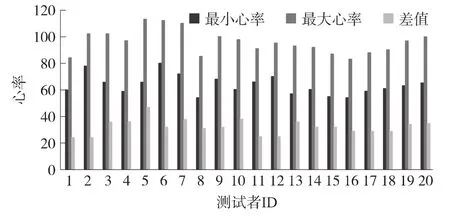
图11 从MIT-BIH ST change和Long-Term ST数据库中选取同一人心电信号的心率变化

3．2 特征提取性能分析

为了探讨算法中原子个数对系统性能的影响，首先对输入的心电模板信号进行FFT-MP稀疏分解得到10个原子的时频参数和其投影值。一般先分解得到的原子的投影值大，取前 n(n=2，3，4，5，6)原子的时频参数γ=(s，u，v，w)和其投影值作为单个心跳周期心电信号的特征参数，实验结果如图12所示。

图12 不同原子个数对系统识别率的影响

从图12中可以观察到取前3个原子的时频参数和投影值可以获得最好的识别效果，心跳识别率和系统识别率最高，随着原子数目的增加，系统识别性能逐渐降低。

一个原子的波形是由其时频参数 γ=(s，u，v，w)决定的，这4个参数对原子的波形的贡献各不相同。原子的投影值反映了该原子在原始信号或者剩余分量所占的比例，对系统识别率也有一定的影响。下面实验讨论了原子不同参数对识别性能的影响，实验中取前3个原子的特征参数，实验结果如图13所示。可以看到相位因子w对系统的影响不大，且表现出较大的随机性，因此选取前三个原子时频参数中的s，u，v以及投影值p作为单个心跳周期心电模板的特征参数。

3．3 SVM分类器性能分析

SVM的核函数主要有线性核函数、Polynomial核函数、RBF核函数和sigmoid核函数。核函数的参数选取选用交叉验证法进行自适应最优选取，实验结果如图14所示。

图13 原子的不同参数选取对系统识别的影响

图14 SVM核函数对系统识别的影响

从图14可以观察到，当选取线性核函数时识别效果最好，因此选取线性核函数作为SVM的核函数，并采用交叉验证法对相关参数进行自适应最优选取。通过实验本算法中参数设定为:选取前三个原子时频参数中的s，u，v以及投影值p作为单个心跳周期的特征参数，SVM核函数选取线性核函数，算法在3个心电数据库中测试性能如表2所示。

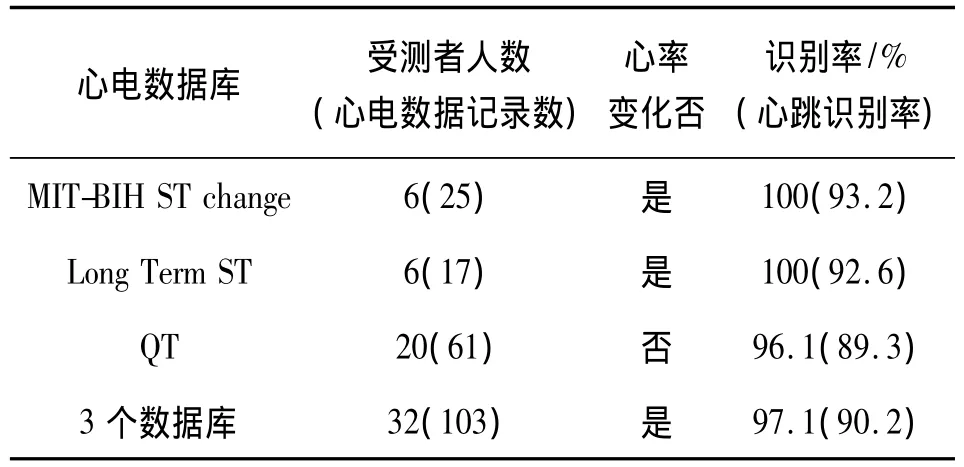
表2 FFT-MP心电特征提取算法在3个数据库中的识别性能

4 结论

心电信号与其他生物特征相比有着更高的安全性，不易伪造，有着较大的发展潜力。本文提出了基于FFT-MP的心电特征提取算法，主要包含预处理、特征提取和分类三部分。预处理消除噪声和心率变异性的影响，并对提取的心电模板进行质量评估;选取单周期的心电信号经过FFT-MP稀疏分解后的前三个原子的时频参数和投影值作为特征参数，构建SVM分类器完成身份识别。采用MIT-BIH心电数据库对该算法进行验证，获得了较好的识别效果。

[1]Xiao Qinghan．Biometrics-Technology，Application，Challenge，and Computational Intelligence Solutions[J]．IEEE Computational Intelligence Magazine，2007，2(2):5－25．

[2]Tsutomu Matsumoto，Hiroyuki Matsumoto，Koji Yamada，et al．Impact of Artificial“Gummy”Fingers on Fingerprint Systems[J]．Proceedings of SPIE，2002，275－289．

[3]Nixon K，Aimale V，Rowe R．Handbook of Biometrics:Spoof Detection Schemes[M]．Springer，2008，403－423．

[4]Kenneth R，MagalhaesD，TenreiroS．CognitiveBiometrics:Challenges for the future[C]//Braga:ICGS3 2010’6，2010:79－86．

[5]Kenneth R，Farzin D，Konstantinos S．Biosignals for User Authentication-Towards Cognitive Biometrics?[C]//Canterbury:2010 International Conference on Emerging Security Technologies，EST 2010，2010:71－76．

[6]Biel L，Pettersson O，Philipson L，et al．ECG Analysis:A New Approach in Human Identification[C]//Venice:IEEE Instrumentation and Measurement Technology Conference，2001:808－812．

[7]Wang Y，Plataniotis K N，Hatzinakos D．Integrating Analytic and Appearance Attributes for Human Identification from ECG Signal[C]//Baltimore:Biometrics Symposiums(BSYM)，2006:1－6．

[8]Li Ming，Narayanan S．Robust ECG Biometrics by Fusing Temporal and Cepstral Information[C]//Istanbul:International Conference on Pattern Recognition ICPR’20，2010:1326－1329．

[9]杨向林，严洪，李延军，等．基于小波分解和数据融合方法的ECG身份识别[J]．航天医学与医学工程，2009，22(4):296－301．

[10]Platanioatis K，Hatzinaos D，Lee J．ECG Biometric Recognition without Fiducial Detection[C]//Baltimore:Biometrics Symposium BCC’06，2006:19－21．

[11]Mallat S，Zhang Z．Matching Pursuit with Time-Frequency Dictionaries[J]．IEEE Trans on Signal Proeessing，1993，41(12):3397－3415．

[12]Arthur P L，Philipos C L．Voiced/Unvoiced Speech Discrimination in Noise Using Gabor Atomic Decomposition[C]//HongKong:Proc of IEEE ICASSP，2003:820－828．

[13]TarvainenM，Ranta-Aho P，Karjalainen P．An Advanced Detrending Method with Application to HRV Analysis[J]．IEEE Trans Biomed Eng，2002，49(2):172－175．

[14]赵治栋，陈裕泉．广义小波收缩消噪阈值选择及应用研究[J]．传感技术学报，2007，20(3):601－605．

[15]纪震，郑秀玉，罗军，等．基于双正交样条小波的QRS波检测[J]．深圳大学学报理工版，2008，25(2):167－172．

[16]王立传，陈裕泉．基于小波变换的QT检测[J]．传感技术学报，2006，19(3):625－628．

[17]叶继伦，郑崇勋，黄燕．心率变化对心电信号各波间期的影响分析[J]．生物医学工程学杂志，1999，16(1):50．

[18]Sethares W A，Staley T W．Periodicity Transforms[J]．IEEE Trans on Sig Proc，1999，47(11):2 953－2 964．

[19]Vapnik V N．Statistical Learning Theory[M]．New York:Wiley，1998．

[20]The MIT-BIH Database．http://physionet．org/physiobank/database．

[21]尹忠科，邵君，Pierre Vandergheynst，等．利用FFT实现基于MP的信号稀疏分解[J]．电子信息学报，2006，28(4):614－618．