基于PSO-SVM的煤岩声发射源定位预测*

单亚锋，孙 朋，徐耀松，付 华，谢 森

(辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105)

随着国民经济的发展，煤炭资源的开采强度和深度与日俱增。但是采空区煤岩体的坍塌以其突发性和巨大的破坏性，对煤矿的安全高效生产造成了极大威胁，因此，对煤岩体进行有效的监测和预测，成为了煤矿安全生产急需解决的问题。

岩石等固体材料在外界作用力下，可能把岩石内部的缺陷激活，从而会造成煤岩体的破坏、损伤，岩石在破坏过程中释放出了应变能，并且这种能量以弹性波的形式快速释放传播，这种现象称为声发射[1]。近年来随着研究的深入，科技的进步，先进的监测方法和手段被应用到煤岩体声发射源定位的监测和预测中，实现了对岩体破裂过程的连续监测，进而来评价岩体的稳定性和危险性，取得了一定的成果[2]。相关的研究表明，声发射与煤岩体破坏过程有很好的相关性，与岩体的内部的损伤有直接关系，声发射事件的累积量是岩体损伤程度的一个重要标志。因此，通过对煤岩的声发射信号的分析和研究，在推断煤岩内部的形态变化的同时，也可反演出即将发生破坏的煤岩体的位置。虽然国内外很多的学者对声发射源的定位做了很多的工作，成新民，胡峰[3]等采用代数网络和混沌参数的碰摩来实现声发射源的定位;康玉梅，刘建坡[4]等采用最小二乘法的算法来定位声发射源;Geiger定位方法[5－6];樊保圣，闫小青[7]等利用 Lamb波频散特性的薄板对声发射源定位方法的研究，还有杨永杰，王德超[8]等利用小波分析对灰岩的声发射进行研究，李怀珍，袁瑞甫[9]利用神经网络的算法和声发射技术结合。但是基于传统的定位算法都具有漏定位，伪定位和定位精度低的缺陷，并且有很大的误差，比如BP算法在网络训练阶段的训练时间较长、很容易进入局部极小和精度不高的弊端。特别是从AE源到传感器检测到的AE信号之间的映射是非线性的，所以传统的算法很难对这些非线性的过程建模，因此，也就很难确定时间差。从而出现了声发射技术在采空区煤岩体灾害预测失灵的现象，大大的降低了声发射预测技术实用化的进程。

支持向量机(SVM)是基于统计学习理论的一种智能学习方法，可以用来解决样本空间的高度非线性的模式识别等问题。本文基于从山西焦煤的官地矿16403工作面获得的声发射事件的数据，采用粒子群优化PSO(Particle Swarm Optimization)的支持向量SVM(Support Vector Machine)理论对声发射事件进行预测，试验结果表明，不仅能够很好的实现声发射源的定位，而且能够很好的解决小样本、高维数和非线性的问题，这对加深煤岩体灾害的发生体制的认识，以及实现更好的、有效的预测提供了新方法，对煤矿的安全高效的运行，减少人员财产的损失提供了理论支持。

1 声发射源定位原理

1．1 声发射数据信号的处理

本文根据山西焦煤的官地矿16403工作面采空区煤岩体的声发射数据信息，采用了PXWAE数字化的声发射检测仪，这套检测仪器包括传感器(频率150 kHz)，前置放大器(增益为40 dB)，主放大器(增益为0 dB)和采集卡，采集到200个采样点原始数据，如图1所示。

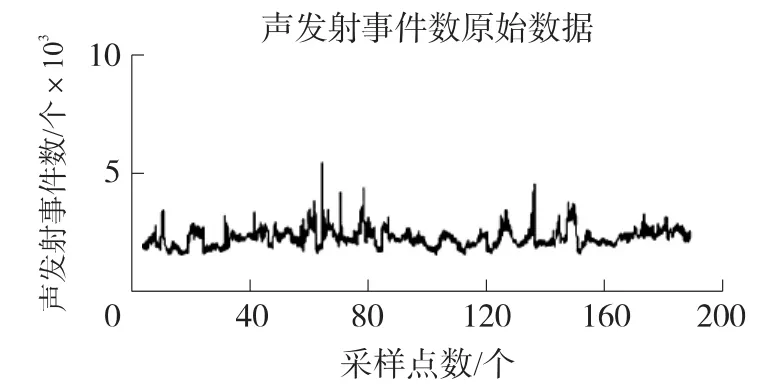
图1 原始声发射信号数据线

准确的提取到煤岩体的声发射信号是预测的首要，但是在实际的煤矿巷道内会存在很多的噪音，如机器的，管道的，支架和工人的声音信号。所以要准确的确定声源的位置，必须对获得的声音信号进行去噪处理。

文中采用了具有较高的分辨率，较好的去相关性和选基灵活性的小波，它不仅能有效的区分信号中的突变成分和噪声，而且可以更好的刻画信号的非平稳特征。为了使获得的数据更能反映煤岩体的状态，以便能更准确的确定其位置，采用软阈值法小波去噪，其公式如(1)。

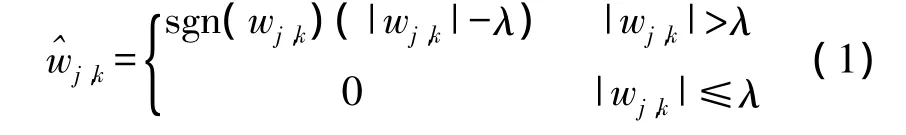
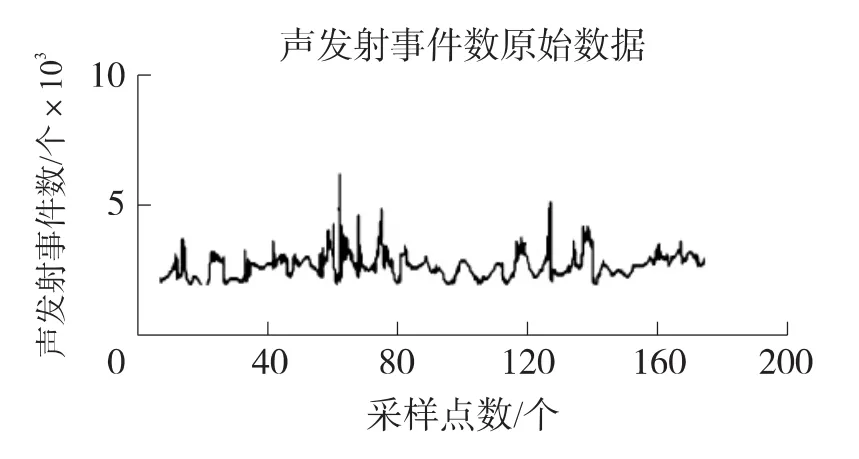
图2 经小波去噪后的仿真图

由图2可以看出，经其去噪后，干扰信号大大减少，具有较好的连续性，可以更方便的处理获得的声发射数据信息。

1．2 相空间重构

1．2．1 最佳延迟时间的确定

采用自相关函数法来计算最佳的时延估计τ，其计算公式为

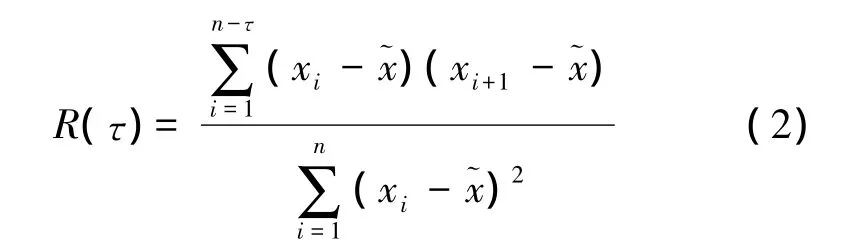
1．2．2 SVM 的预测原理

虽然现在很多的方法可以计算最佳嵌入维数，例如虚假邻域法[11]，预测误差最小法，G－P算法[12]，伪最邻近点法，关联积分法等，文中采用了最小预测误差法，将延时向量写为:

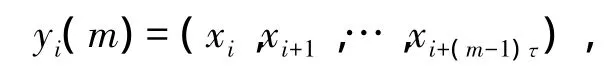
其中，τ为最佳的延迟时间，yi(m+1)=(xi，xi+τ，…，xi+mτ);yn(i，m)(m)是离轨线 yi(m)最近的向量;‖·‖表示欧式距离下的最大值范数，yi(m+1)为嵌入维数等于 m时的第 i个时间延迟向量，且必须满足1≤n(i，m)≤n－mτ。根据均值公式

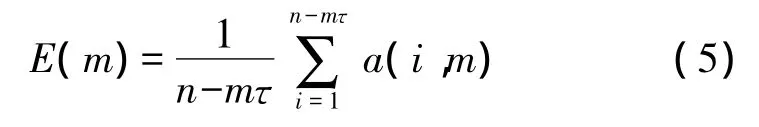
为获得最佳的嵌入维数，利用式(4)

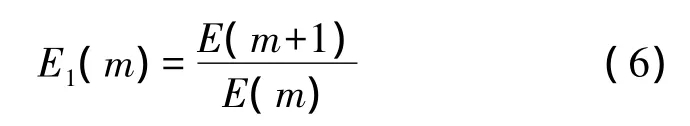
当E1(m)不再变化时，此时的最佳维数为m+1。

将得到的训练样本集映射到高维特征空间，使得非线性问题变成高维的、线性的问题，设SVM的估计函数为f(x)=wTφ(x)+b;支持向量机的回归问题变为:

约束条件为:

1．2．3 PSO的SVM的参数优化

在SVM的声发射源的定位模型中，参数的选择对整个定位精度的影响至关重要，因此，选择最佳的参数是预测的前提之一，所以，对于损失函数ε、惩罚因子C和核函数σ选取进行了粒子群优化，参数的具体优化步骤如下[14]:①初始化各参数，设置粒子数、循环次数、搜索范围、w、c1和 c2等;②根据试算确定(C，σ)的范围，初始化所有粒子，并设置其初始位置pbest(gbest为其中的最优值)和速度;③计算粒子的适应值，确定每个粒子的最优适应值和全局最优适应值，并应用比较替换的方法，确定其最后的取值;④反复的验证迭代，找到最佳的解，测试是否满足结束的条件，若满足则结束，否则重复上式更新粒子的速度和位置;⑤建立预测模型，将满足结果的全局最优粒子所对应的ε、C和σ作为最终的值，并建立相应的PSOSVM预测模型。

2 基于PSO-SVM的声发射源定位预测

2．1 模型预测

SVM的真正价值的应用是用来解决非线性问题的，将实测到的声发射事件数作为事件序列x=[xi]，利用相空间重构获得的嵌入维数m，将m作为支持向量机输入的特征节点来构建训练样本

所以经训练学习后，根据PSO-SVM建立的预测模型为

式中:n为训练样本数，这样经过SVM就把这样一个高维、非线性的问题转化成二维的线性的问题[15]，经过上式的计算，然后把煤岩体和岩石的声发射总数整合，同一位置声发射事件总数最多，说明其点的岩石越不稳定，从而可以做出预测，实现了“1+1=1”的想法。

2．2 PSO-SVM在声发射源的预测应用

声发射源定位就是根据PSO-SVM建立的预测模型来收集煤岩和岩石发出的总声声发射事件数，来判断此时煤岩体的状态，因为即将失稳的区域的煤岩体和岩体都会极度的不稳定，发出的声发射信号会很多，因此，通过设定标定值，将收集到煤岩体声发射信号和岩体的声发射信号分别列出，然后将两者的声发射信号总数分为两种，一是正常;二是超标。当这个数值超过设定的标定值(4 000为临界值)，就用前面最佳延迟时间求出其具体的位置，并通过报警的方式告知在那个区域的工作人员，以便做好相应的防范措施，这就是通过PSO-SVM声发射源定位的“1+1=1”思想，即通过分析同一位置的煤岩体和岩体的声发射信号，反演出即将失稳的岩体的位置。

本文收集了山西焦煤的官地矿16403工作面25个不同位置煤岩体和岩石的声发射信号，取前20个样本作为PSO-SVM的训练样本，后5个样本作为测试样本，首先对样本进行归一化验证，试算确定PSO的参数如下:粒子个数为40;粒子维数为3;循环次数为150;学习因子 c1=1．6，c2=1．8;参数 C 的搜索范围为(0．1，100);参数 σ的搜索范围为(0.01，1000)。经过PSO优化，最终确定SVM的最优参数为 C=6．58，σ2=0．126，ε =0．0256。利用PSO-SVM的预测模型对20组煤岩体和岩石的声发射信号进行分析处理。

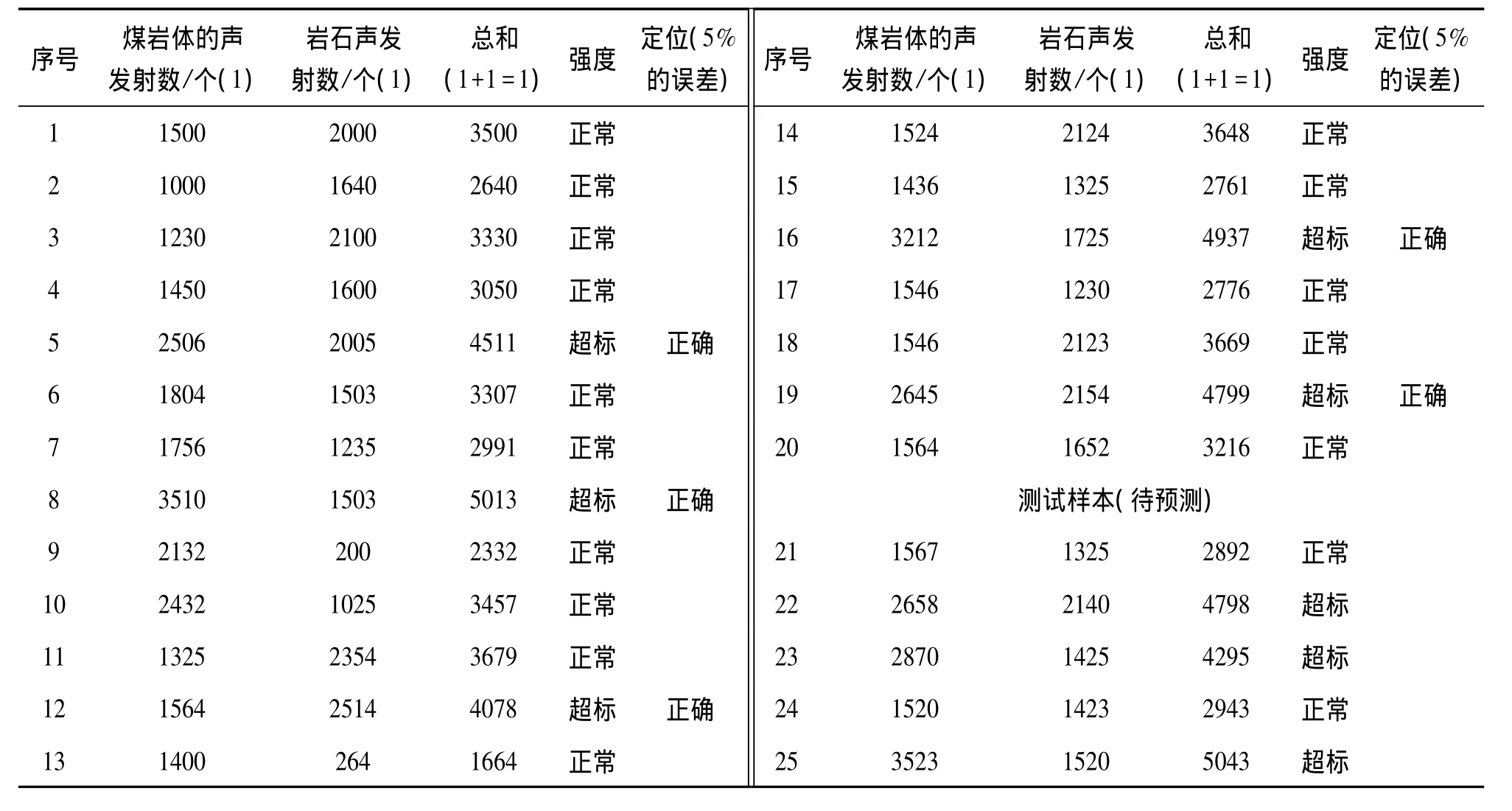
表1 声发射事件的SVM训练样本

利用获得的最优参数来建立支持向量机模型，对5个采样点测试样本进行预测，其仿真结果如下图3所示。

图3 测试样本的SVM仿真结果

从图3可以看出，共有5组测试样本，使用粒子群进行优化的支持向量机预测模型，分别对煤岩体的声发射事件数和岩石的声发射事件数进行了预测，除了一个有较大点的偏差外，其余测试值基本上和实际值吻合，预测的正确率为80%。根据两者声发射的总数，反演超过标准值的声发射数所在的位置，利用前面计算的最佳时延估计τ，推出其位置。

对测试样本中声发射事件数超过标定值的22、23、25号采样点进行了声发射源的反演定位，由上图可知，经过其优化后，定位精度为85．45%，最大定位误差为4．68%。所以通过对其进行研究，将为煤岩的安全监测提供了一个新的方法，从而为煤矿的安全运行、保护人身财产安全提供新的理论依据。

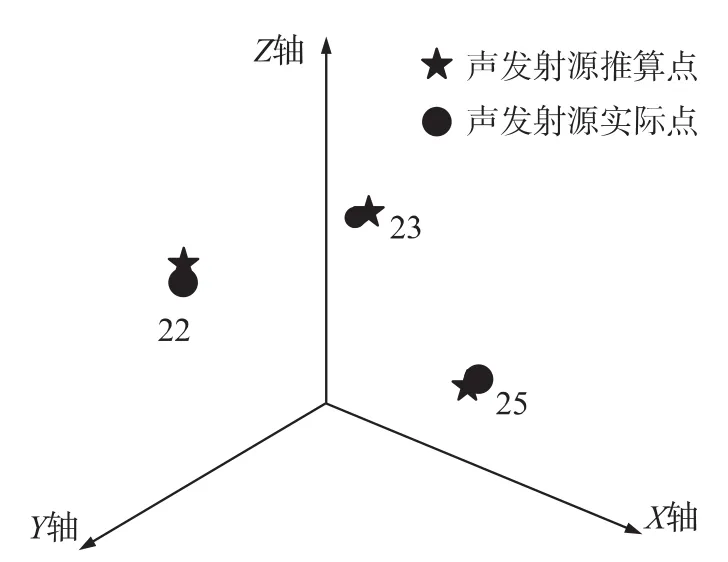
图4 测试样本的定位结果

3 结论

(1)将PSO-SVM理论引入到煤岩声发射源的研究中，提出了声发射源定位的SVM模型，并且很好的解决了声发射源与其影响因子之间的小样本、非线性等数据的问题。

(2)SVM方法能够充分发挥训练样本的分布特点，根据获得的训练样本建立预测模型，不需要太多的经验和使用技巧，具有较高的全局最优性和较强的泛化能力。本文采用PSO对SVM的参数进行了优化，选取了最优参数，通过仿真结果和定位结果表明，经过其优化后，煤岩声发射事件预测精确，从而大大提高了声发射源的定位精度，能够很好的解决高维、非线性问题。

(3)文章通过对收集到的声发射事件数据信息，进行去噪、相空间重构、建立预测模型，实例应用和仿真分析，首次提出了“1+1=1”的定位模式，即通过对同一地点的煤岩体和岩石的声发射信号的分析处理，反演出即将失稳的煤岩体的位置，因为即将失稳的区域煤岩体和岩石都是不稳定的，摆脱了以往单独的分析煤岩体，岩体的模式禁锢，仿真结果表明经过粒子群优化过的支持向量机在煤矿煤岩声发射源定位模型是一种可行、有效和准确的预测理论方法。

[1]Lockner D．The Role of Acoustic Emission in the Study of Rock Fracture[J]．International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1993，30(7):883－899．

[2]李世愚，和雪松，张天中，等．地震学在减轻矿山地质灾害中的应用进展[J]．国际地震动态，2006(4):2－9．

[3]成新民，胡峰，邓艾东，等．基于代数网络和混沌参数的碰摩声发射源定位方法研究[J]．振动工程学报，2011，24(3):287－293．

[4]康玉梅，刘建坡，李海滨，等．一类基于最小二乘法的声发射源组合定位算法[J]．东北大学学报，2010，31(11):1648－1656．

[5]Geiger L．Probability Method for the Determination of Earthquake Epicenters from the Arrival Time Only[J]．Bull StLouis Unic，1912，8:60－71．

[6]Geiger L．Herbsetimmung Bei Erdbeben Aus Den Ankunfzeiten[J]．Gessell Wiss Goett，1910，4:331－349．

[7]樊保圣，闫小青，余丽，等．基于Lamb波频散特性的薄板声发射源定位方法研究[J]．固体力学学报，2011，32:283－287．

[8]杨永杰，王德超，陈绍杰，等．基于离散小波分析的灰岩压缩破坏声发射预测研究[J]．煤炭学报，2010，35(2):213－217．

[9]李怀珍，袁瑞甫．基于神经网络的声发射定位技术及在岩石破裂实验中的应用[J]．矿业工程，2005，3(5):3－5．

[10]Rosenstern M T，Collins J J，Deluca C J．A Practical Method for Calculating Largest Lyapunov Exponents from Small Data Sets[J]．Physical D，1993，65:117－134．

[11]王妍，徐伟，曲继圣．基于时间序列的相空间重构算法及验证(一)[J]．山东大学学报，2005，35(4):109－114．

[12]Grassberger P，Procaccia L．Measuring the Strangeness if Strange Attractors[J]．Physica D，1983，9:189－208．

[13]张朝龙，江巨浪，李彦梅，等．基于云粒子群－最小二乘支持向量机的传感器温度补偿[J]．传感技术学报，2012，25(4):472－477．

[14]王涛，王洋洋，郭长娜，等．QGA-RBF神经网络在矿井瓦斯涌出量预测中的应用[J]．传感技术学报，2012，25(1):119－123．

[15]黄存捍，冯涛，王卫军，等．基于分形和支持向量机矿井涌水量的预测[J]．煤炭学报，2010，35(5):806－810．