浅谈初中数学变式拓展问题

张晓静

当前课堂教学中，部分教师在选取试题作为某课知识点的辅助练习时，常选用近几年的中考试题，而且以试题的数量多少来衡量本节课的容量。当然中考试题典型，有代表性，说服力强，可是如果只是一味的用中考试题来罗列，知识既零散又重复，学生很难抓住重点，学习的知识没有系统性，课堂的效果也不会高效。因此，课上的问题要进行必要的变式，拓展。

例如，在复习全等三角形一节时，我以一道改装的中考题为例，从以下两方面入手，和学生共同分析探讨。

第一方面：巩固知识点，讲授传统知识

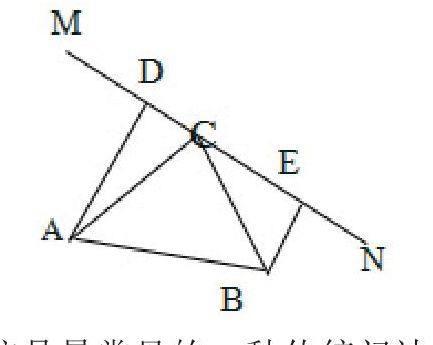
例：如图，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，求证（1）△ADC≌△CEB， （2）：DE=AD+BE。

这是最常见的一种传统问法，有目的性，为达目的而去寻找条件，使问题得以解决，问题（1）并不难解决，学生可独立完成；问题（2）是性质的简单应用，稍作转化，学生交流后也可解决。

第二方面：添加情境，再探此题，在传统题的基础上，添加情境。

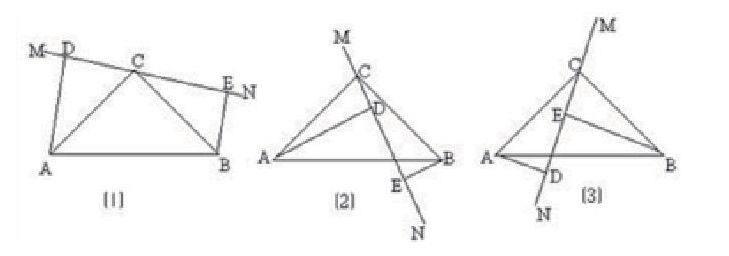
如果认为直线MN在动，上述的问法将变为以下3种。

（1）当直线MN绕点C旋转到如图（1）所示的位置时，请说明△ADC≌△CEB， DE=AD+BE。

问：在解决它时，与前面的问法在解答时有变化吗？

将上述传统问法自然地过渡到情境的问题中。

（2）当直线MN绕点C旋转到图（2）所示的位置时，请说明DE=AD-BE的等量关系成立。

这问比（1）问加深一层，先让学生独立思考，然后讨论交流，如果学生仍觉得有困难，可适当引导。问：在这个图形中，△ADC与△CEB还有全等关系吗？设计这道题的目的是要让学生注意前后知识的联系，加入情境后，还能够挖掘出此题的内涵。

（3）当直线MN绕点C旋转到图（3）的位置时，试问DE、AD、BE之间有何关系？

这问比（2）又加深一层，与开始的传统问法相比，没有了直接目的，只有探索猜测，然而经历了前两问的铺垫，问题的得出就显得很顺畅了。这3个问题环环相扣、循序渐进，探索的目的达到了，难点也突破了。

这样处理，看似只是一道题，可容量无形中加大了，还体现了由静到动的过程。让学生在解决问题的过程中继续进行探索活动，将探究活动向课外拓展、延伸，不但可激发学生的求知欲，而且可以在他们已有知识认知的基础上进一步升华，反过来促进课堂教学，往往还能在师生探讨的过程中，迸发出意想不到的结果，教学相长.因此在教学的过程中可适当的将一些练习进行变式.

教育专家们常说，教学有法，教无定法。无论是哪种教学方法，都应该实现两个教学目标，一是在有效的时间内教学生学会规定的内容，二是通过拓展教学引导学生学会学习，达到理念的升华，能力的拓展。我们教学要以培养学习能力为重点，狠抓学习基本环节，寓学法指导于教学活动之中；拓展教学中让学生掌握函数方程、分类整合、数形结合、化归转化、特殊一般等数学思想和换元法、配方法、待定系数法、分析法、归纳法等数学方法。在传授、启发、探究、交流中，都要以激发学生学习兴趣为目的，使学生产生一种掌握知识的欲望。鼓励学生提出问题和开展探究活动，在获取知识的过程中学会学习、学会思考.