谈建模教学在小学数学教学中的应用
徐荣花
摘 要:数学建模是近年来数学教学中一个热点现象,很多学校都在广泛开展数学建模教学活动。在小学数学教学中开展建模教学,不仅是素质教育的需要,也是《义务教育数学课程标准》提出的要求。
关键词:数学建模;学习过程;数学思想
《义务教育数学课程标准》在前言中指出:数学“有助于人们收集、整理、描述信息,建立数学模型,进而解决问题”,小学数学教学要“从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程”。那么,如何理解小学数学建模并在教学中实践数学建模呢?
一、正确认识数学建模
当前,鉴于数学建模思想在多种领域中的应用价值,越来越多的学者投身于数学建模理论的研究。综合多种说法来理解,所谓数学建模,即是用数学式子(数学模型)来表述实际问题,再通过计算得到的模型结果来解释实际问题的全过程。
小学数学建模是以体验数学活动为目的,帮助学生掌握新知。
由于小学生的知识背景有限,以重复前人的数学活动为主,且作为一种教学策略开展。
二、小学数学建模的策略
1.创设生活化的问题情境
小学数学中的公式、法则和定律等本身就是数学模型。小学生心理不成熟,对纯理论的内容接受能力较低,却对生活充满好奇。针对这一特点,在数学建模中首先要创设出一个生活化的问题情境,引起学生的关注,诱发问题。例如,教材中关于“从一点画一条已知直线的垂线”的内容,对小学生来说,内容稍显生硬,不易激发兴趣。若改成“从某村庄修一条到公路的小路,怎样走最近?”的问题来,则显得生动活泼,极大地调动了学生参与建模手的积极性。
2.启发、指导构建模型
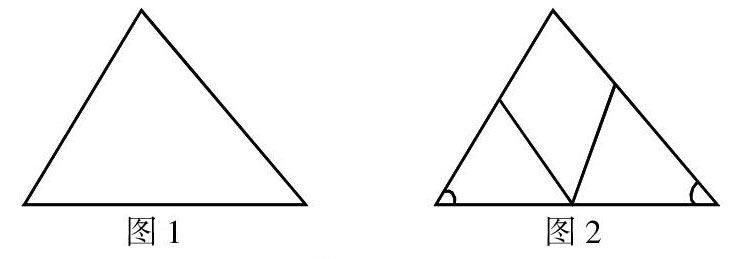
数学建模过程,需要具体化、直观化的问题抽象化,然后用不完全归纳法构建出数学模型。例如学习“三角形内角和”,我发给每个小组一块泡沫板、长直尺、小刀、量角器,让他们使用手中的工具测量出三角形的内角和。那么,首先要先得到一个三角形,各组立刻利用尺子和小刀把泡沫板切成了三角形(如图1)。很多学生提出用量角器测量,然后我提出:“没错,用量角器是个好办法,但那样要量角三次,你有没有办法只量一次就知道三角形内角和是多少?”在思考过后,几个学生提出“要是能把几个角‘加在一起就好了,就能只量一次了。”我立刻鼓励他们动手把三个角“加”起来试试看。经过小组成员的讨论、分析,我看到有的学生开始切割三角形板(如图2),然后把三个角拼接起来准备测量。这时,我听到学生惊喜地说:“老师不用量了,(举起手中的角和直尺)是180°!”
指导小学生构建数学模型,应以启发为主,关注在构建模型过程中学生的思维体验。提出的问题既要有启发性,还要注意难度适中,不能一下子把他们难住,使学生不敢前进。建模是学生分析、抽象、综合、表达能力的综合体现过程,教师要关注在此过程中对学生综合能力的培养。
3.拓展应用模型
当数学模型从具体的问题中被提炼出来以后,原有数学模型的价值已不仅局限于此了,教师应该指导学生在此基础上将模型的应用进行拓展。如学习了“鸡兔同笼”的数学模型后,本着“数学回归生活”的思想,我提出了如下问题:“超市前停放着电动车和三轮车,一共50辆,车轮共110个。停放的电动车和三轮车各多少辆?”
三、小学数学建模的注意事项
1.充分认识到建模主体的儿童性
小学数学建模的主体是小学生,在指导学生建模时,创设的问题情境要充分考虑的学生的“最近发展区”,把握好问题的难度、深度,提出“跳一跳,够得着”的问题来刺激学生思考,调动他们参与学习的积极性。
2.重视学习过程中的体验
可以说,所有的数学概念都能在现实生活找到它的原型,数学就是为了研究世界,解决现实问题而生的。在教学中,我们要多从生活中发掘学生熟悉的数学素材,将生活中常见的数学现象、数学模型呈现在课堂上。
3.循序渐进防止机械强化
数学建模教学最忌“走形式”“走过场”,很多教师舍不得花时间让学生亲历数学建模的“艰苦探索”的过程,过早地将数学模型抽象出来,呈现给学生,然后问一句:“是不是这样啊?”学生再齐声回答:“是。”这样僵硬的学习过程,学生的思维和能力怎能得到发展?数学建模也失去了意义。所以教师在指导学生数学建模时,必须付出极大的耐心,要循序渐进地帮助学生成长。
数学是人们生活、学习和工作的工具,数学思想和方法将伴随人的一生。在学生接触数学的早期,通过指导学生数学建模,向学生渗透数学的思想和方法,必将为孩子的发展奠定扎实的基础。
参考文献:
[1]徐信才.浅谈在小学阶段开展数学建模活动[J].科教导刊, 2009(26).
[2]陈淑娟.浅谈小学数学建模[J].读与写,2011(5).
[3]董美娟.合理定位小学数学建模[J].世纪桥,2012(3).
(作者单位 江苏省张家港市后塍小学)

