相对运动非完整动力学系统的共形不变性与守恒量

王廷志， 韩 月林

(江南大学 理 学院，江苏 无锡214122)

对称性原理是物理学中更高层次的法则，动力学系统的对称性，亦称不变性。用对称性方法研究动力学系统的守恒量，一直是数学物理学科特别是分析力学的一个重要发展方向［1－3］。1997 年，Galiullin A S等在研究Birkhoff系统分析动力学时，提出了Birkhoff方程的共形不变性和共形因子的概念［4］，并讨论了Pfaff作用量在无限小变换下的不变性与共形不变性，Lie对称性与共形不变性之间的关系。近年来，国内学者深入而广泛地研究了动力学系统的Noether对称性，Lie对称性和形式不变性。近期，有了共形不变性在动力学系统中新的应用研究［5－7］。文献［8］研究了变质量 Chetaev 型非完整系统的共形不变性，文献［9］研究了相对运动完整动力学系统的共形不变性与守恒量。本文作者研究相对运动非完整动力学系统的共形不变性与守恒量，推导出相对运动非完整动力学系统的运动微分方程具有共形不变性并且是Lie对称性的充分必要条件，借助规范函数满足的结构方程导出系统相应的守恒量，并给出了应用算例。

1 系统的运动微分方程

设力学系统的位形由n个广义坐标qs(s=1，…，n)来确定，它的运动受有g个理想双面Chetaev型非完整约束

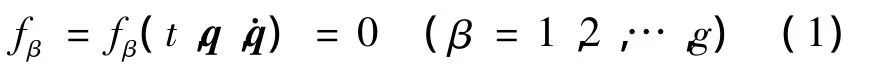
约束方程(1)加在虚位移δqs上的限制为

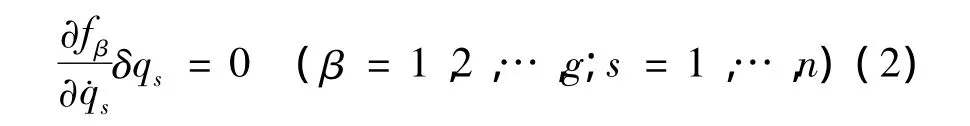
系统的相对运动微分方程可表示为

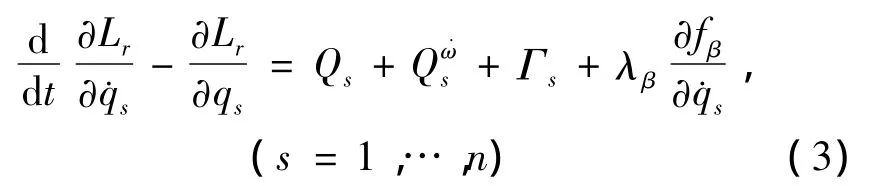
方程中Lr=Lr(t，q，˙q)为系统相对运动的Lagrange函数，Qs=Qs(t，q，˙q)为非势广义力mir′i)·(∂r′i/∂qs)为广义回转惯性力，其中mi为第i个质点的质量，Γs=2˙qkω · (mi(∂r′i/∂qs)×(∂r′i/∂qk))为广义陀螺力，其中ω为载体的角速度，λβ= λβ(t，q，˙q)为 Lagrange 乘子。

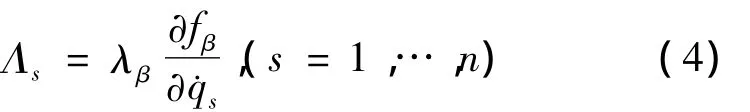
方程(3)可以表示为

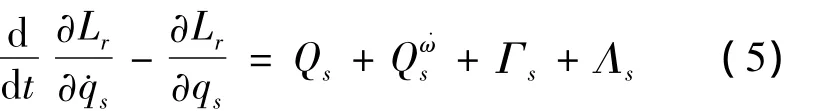
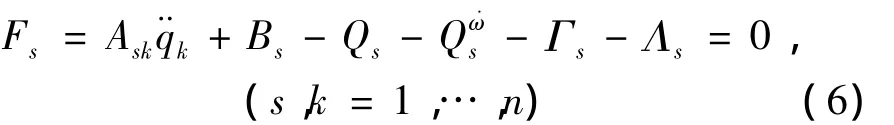
这里

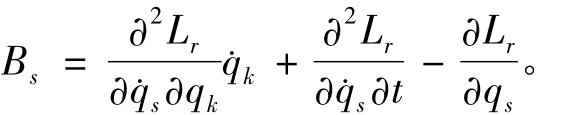
式(6)为相对运动非完整动力学系统(2)(3)相应的完整系统表达式。

根据方程(6)可解出所有的广义加速度

2 系统的共形不变性与共形因子

引入时间和广义坐标的无限小单参数变换群

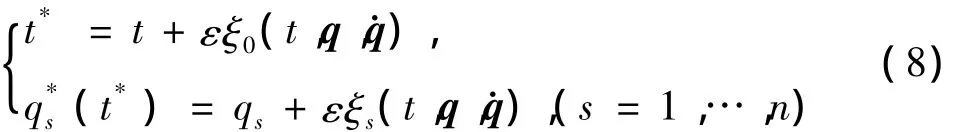
方程(8)中，ε为无限小参数，ξ0，ξs为无限小变换生成元。

定义1［10］二阶微分方程 Fs，在无限小生成元ξ0(t，q)，ξs(t，q)的变换下，若满足则称二阶微分方程为共形不变，是非退化矩阵，

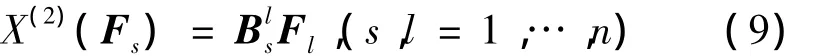
称为共形因子。这里

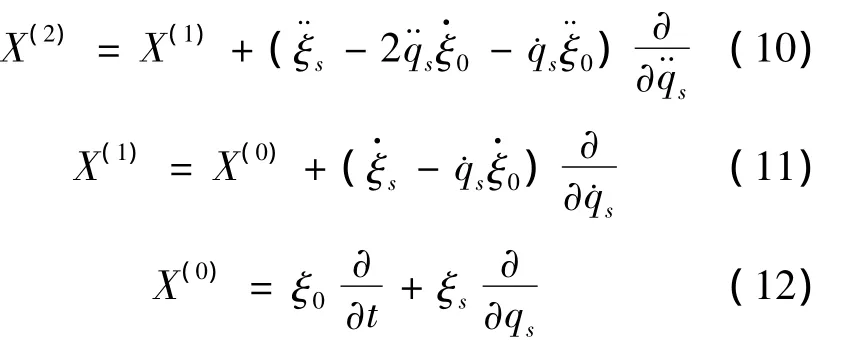
对于相对运动非完整动力学系统(2)(3)相应的完整系统(6)，如果无限小生成元 ξ0(t，q，)，ξs(t，q)满足确定方程

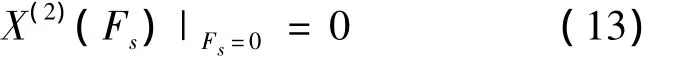
则称这种对称性为系统的Lie对称性。

为求得共形不变性的共形因子，计算差值

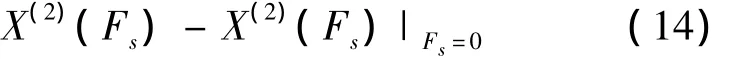
因为

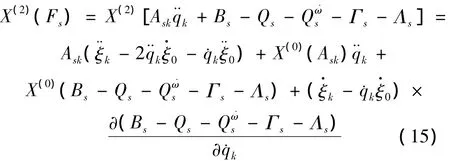
又

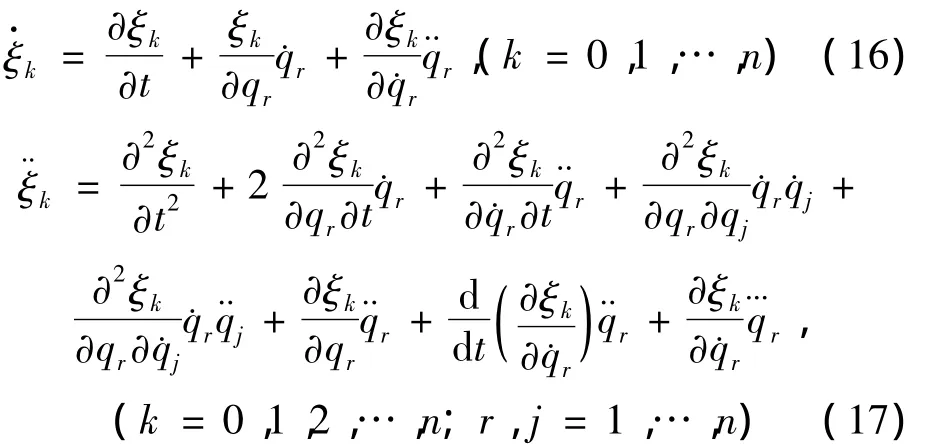
将式(16)(17)代入式(15)，并考虑到Fs=0时=αs(t，q，˙q)，得到

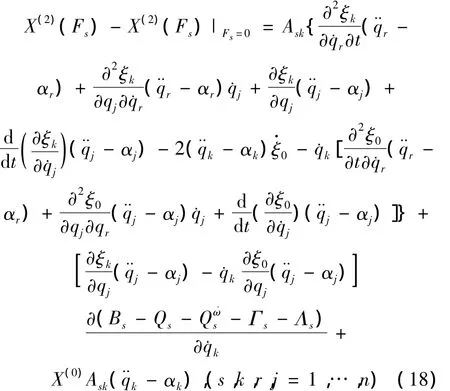
由于

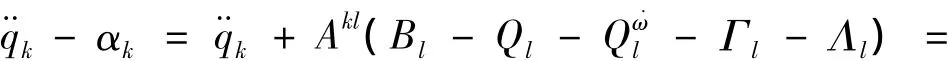
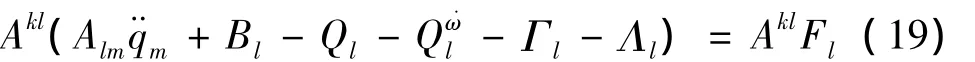
所以

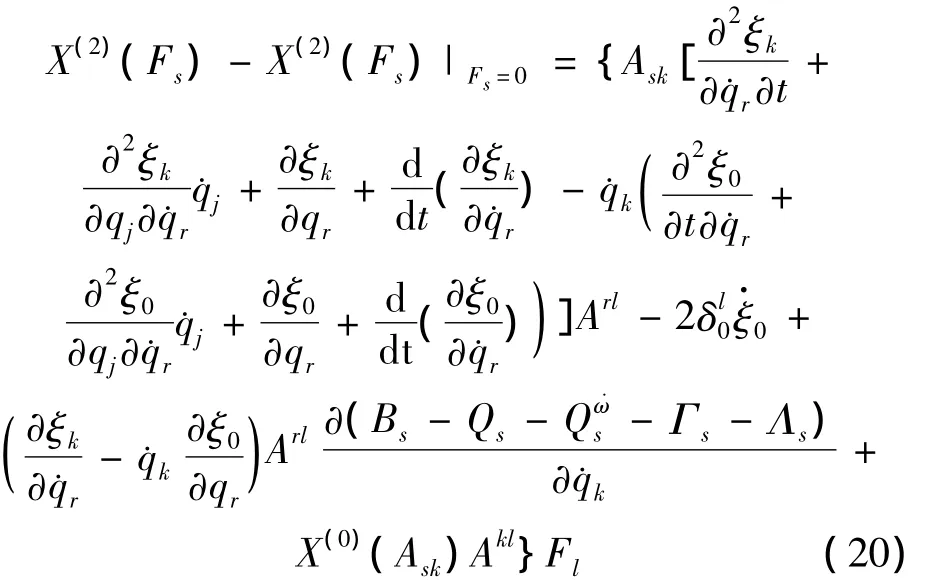
令

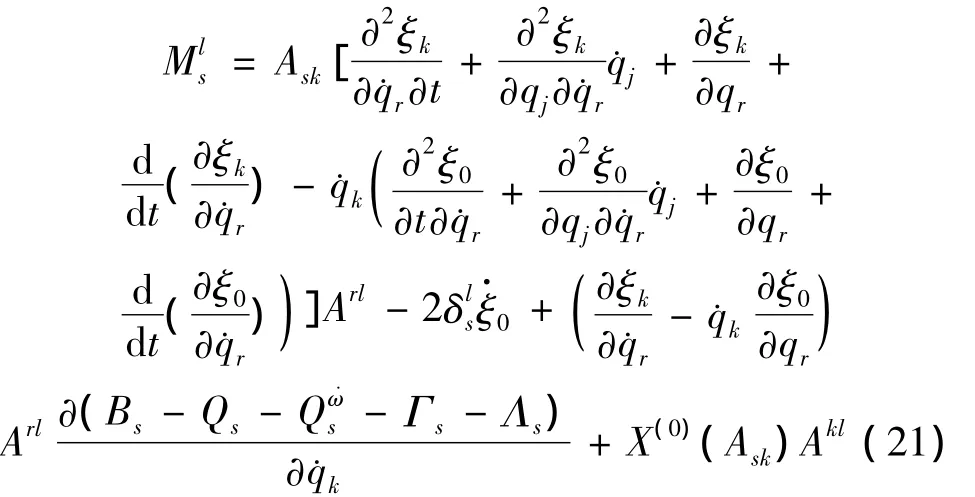
得

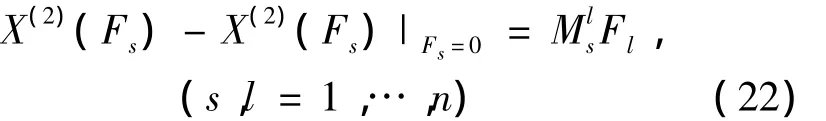
如系统具有共形不变性且是Lie对称性，由式(9)和式(22)可得

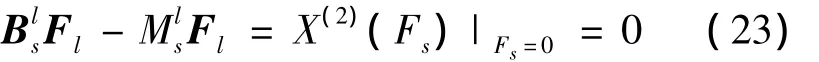
即

命题1 对于相对运动非完整动力学系统，其共形不变性且是Lie对称性的充分必要条件是生成元满足

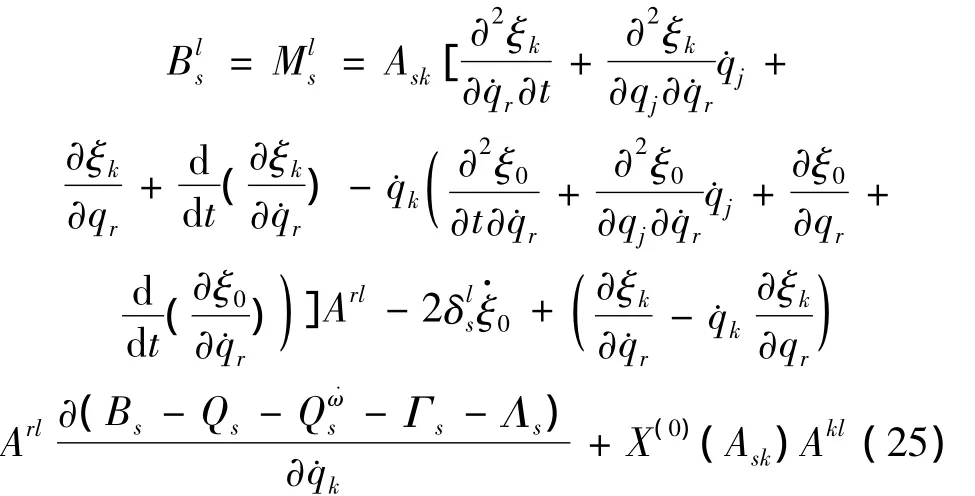
3 共形不变性与守恒量

由相对运动非完整动力学系统的共形不变性，通过Lie对称性可导出相应的守恒量，有如下结论。命题2［11］对于相对运动非完整动力学系统，如果共形不变性的无限小生成元 ξ0(t，q)，ξs(t，q)和规范函数G满足如下Lie对称性的结构方程

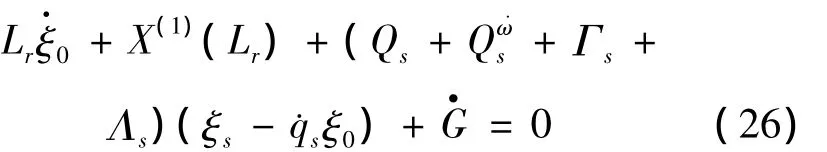
则相应于相对运动非完整动力学系统(2)(3)的完整系统(6)的共形不变性存在守恒量

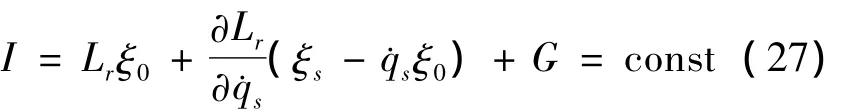
在无限小变换(8)下，非完整约束方程(1)的不变性可表示为限制方程

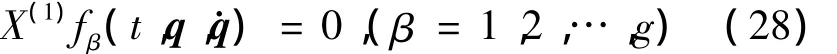
考虑到非完整约束(2)对无限小生成元ξ0(t，q，˙q)，ξs(t，q)的限制，有附加限制方程

定义2 对于相对运动非完整动力学系统，如果无限小生成元 ξ0(t，q)，ξs(t，q)满足确定方程(13)和限制方程(28)，则这种对称性为系统的弱Lie对称性，相应的共形不变性是弱Lie对称性的共形不变性。如果无限小生成元 ξ0(t，q)，ξs(t，q，)满足确定方程(13)、限制方程(28)及附加限制方程(29)，则称这种对称性为系统的强Lie对称性，相应的共形不变性是强Lie对称性的共形不变性。

由命题2可得如下结论:

命题 3 如果 ξ0(t，q)，ξs(t，q)是相对运动非完整动力学系统(2)(3)的弱(强)Lie对称性生成元，且存在规范函数G满足结构方程(26)，则相对运动非完整动力学系统(2)(3)的弱(强)Lie对称性的共形不变性导致守恒量(27)。

4 算例

设一相对运动力学系统为

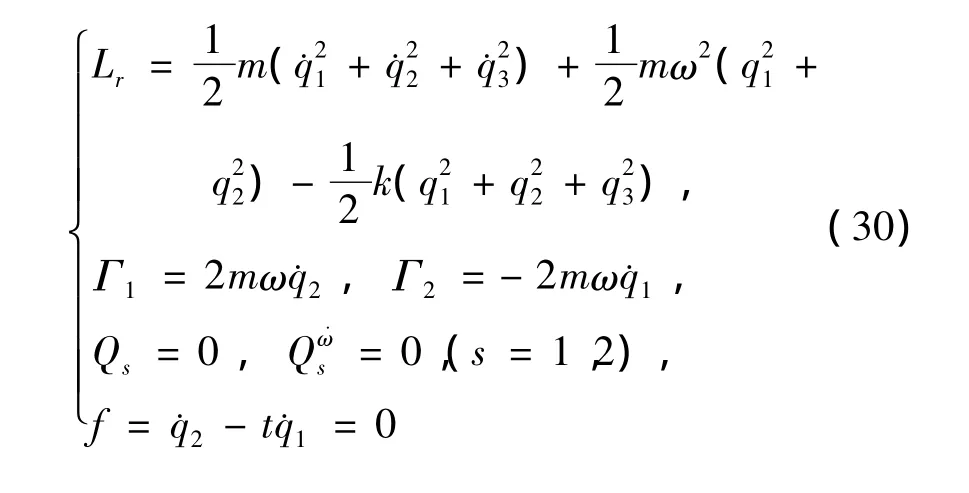
式(30)中k，m，ω为常数，试研究系统的共形不变性与守恒量。

由方程(3)可得

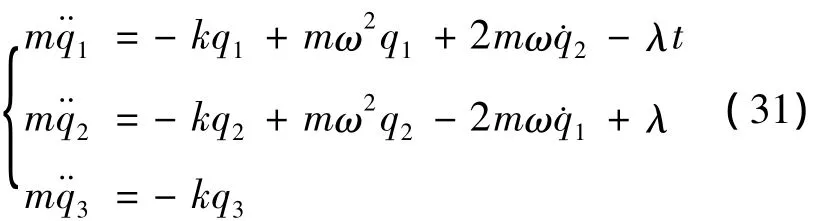
对式(30)最后一式求导，并将式(31)代入可解得

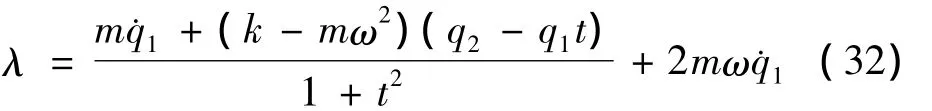
由此得到

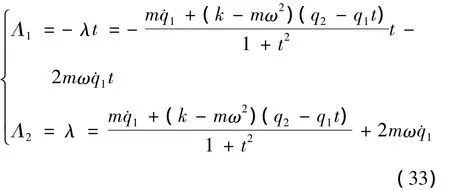
将式(32)代入式(31)，可得系统的微分方程

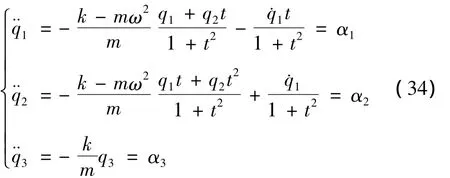
或

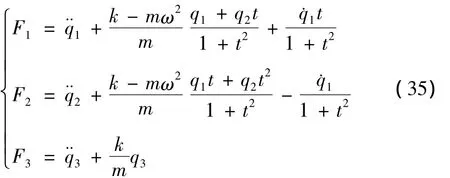
取无限小变换生成元为

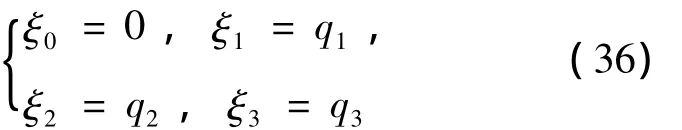
则

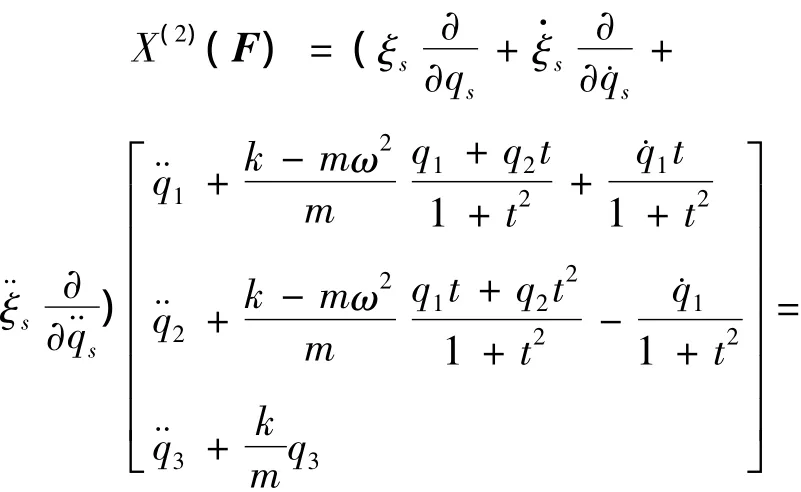
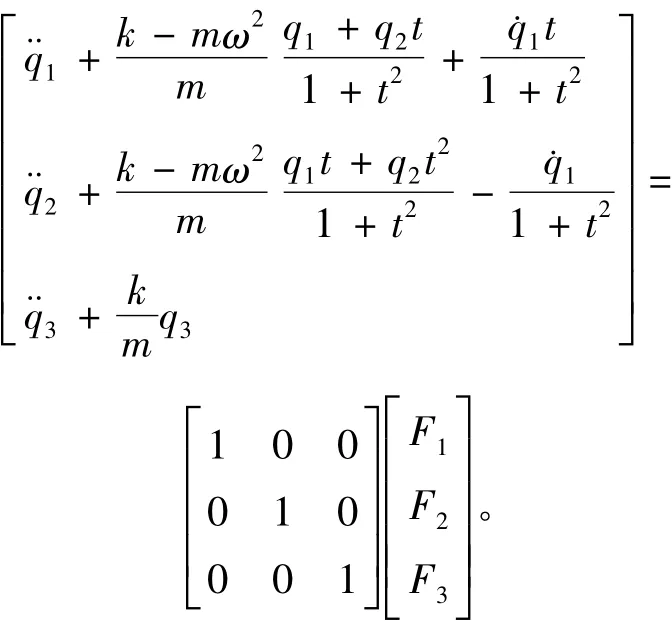
因此，共形因子为

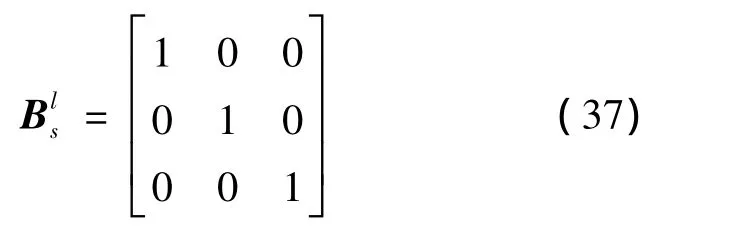
也可从式(25)求出共形因子

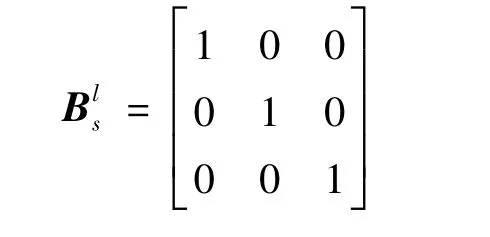
显然与式(37)结果一样，共形不变性确定方程为

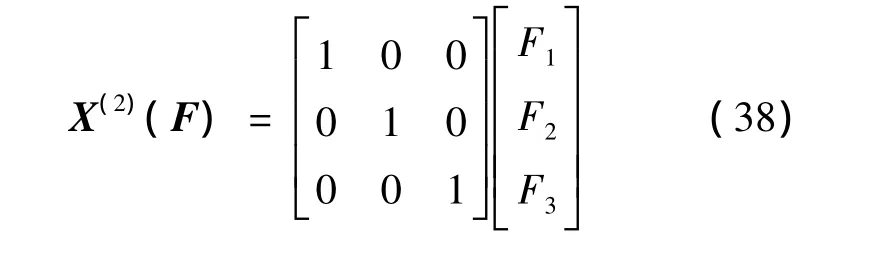
此时，系统既是共形不变性，又是Lie对称性的。显然，相应的对称性是系统的弱Lie对称性，因为生成元满足限制方程(28)，但不满足附加限制方程(29)。

将式(30)、(33)和式(36)代入式(26)可得

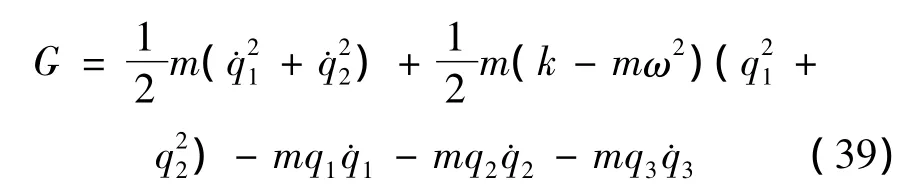
将式(39)代入式(27)，得到守恒量

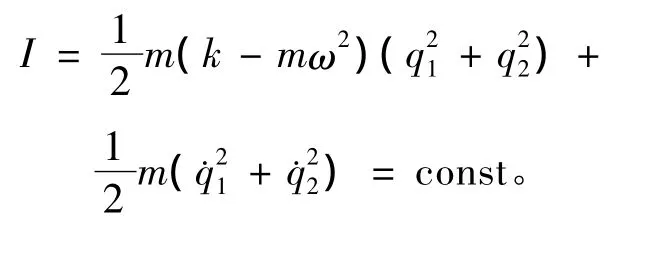
5 结语

对于相对运动非完整动力学系统在无限小变换下的共形不变性，当生成元满足系统的限制方程(28)或限制方程(28)和附加限制方程(29)时，可得到系统弱或强Lie对称性的共形不变性，共形不变性满足一定的条件，可导致相应的守恒量。

［1］梅凤翔，刘瑞，罗勇.高等分析力学［M］.北京:北京理工大学出版社，1991.

［2］NOETHER A E.Invariance variations problem［J］.Nachr Akad Wiss Gttingen，Math Phys，1918 II:235－237.

［3］Lutzky M.Dynamical symmetries and conserved quantities［J］.JPhys A:Math Gen，1979，12(7):973－981.

［4］Galiullin A S，Gafarov G G，Malaishka R P，et al.Analytical dynamics of helmholtz，birkhoff and nambu systems［M］.Moscow:UFN，1997.

［5］张毅，薛纭.完整力学系统的共形不变性与守恒量［J］.力学季刊，2009，30(2):216－221.ZHANG Yi，XUE Yun.Conformal invariance and conserved quantities of holonomicmechanical systems［J］.Chinese Quarterly Of Mechanics，2009，30(2):216－221.(in Chinese)

［6］王肖肖，孙现亭.Chetaev型约束的相对运动力学系统Nielsen方程的Noether对称性与Noether守恒量［J］.物理学报，2012，61(2):064501.WANG Xiao－xiao，SUN Xian－ting.Noether symmetry and Noether conserved quantity of Nielsen equation in a dynamical system of the relativemotion with nonholonomic constraintof Chetaev’s type［J］.Acta Phys Sin，2012，61(2):064501.(in Chinese)

［7］CAIJian－le，SHISheng－shui，FANG Hua－ji.Conformal invariance for the nonholonomic constrained mechanical system of non－Chetaev’s type［J］.Meccanica，2012，47:63－69.

［8］黄卫立，蔡建乐.变质量Chetaev型非完整系统的共形不变性［J］.应用数学和力学，2012，33(11)1294－1303.HUANGWei－li，CAI Jian－le.Conformal invariance for the nonholonomic system of Chetaev’s type with variable mass［J］.Applied Mathematics and Mechanics，2012，33(11)1294－1303.(in Chinese)

［9］CHEN Xiang－wei，ZHAO Yong－hong，LI Yan－min.Conformal invariance and conserved quantities of dynamical system of relativemotion［J］.Chinese Physics B，2009，18(08):3139－06.

［10］蔡建乐，梅风翔.Lagrange系统Lie点变换下的共形不变性与守恒量［J］.物理学报，2008，57(9):5369－5373.CAIJian－le，MEIFeng－xiang.Conform in variance and conserved quantities of Lagrange systems under Lie point transtormation［J］.Acta Physica Sinica，2008，57(9):5369－5373.(in Chinese)

［11］梅风翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.