基于比率依赖的两种群捕食者—食饵系统的随机模型的渐近性质*
史 超,谭 杨,郭子君
(1.华南农业大学应用数学研究所,广东 广州 510642;2.铜仁职业技术学院,贵州 铜仁 554300)
生物种群的状态特征分析是数学生态学的中心工作之一。在数学生态学的研究中,种群的持续生存一直以来都是一个很受关注的重要问题。自从Lotka和Volterra提出标准的两种群Lotka-Volterra系统以来,已经有很多学者对此进行了大量的研究,并得到了很多研究成果。对于这个系统,如果其中的a12>0,a21<0,这就是标准的Lotka-Volterra型捕食者—食饵系统。近年来根据生物学和生理学中研究的数据表明:一个合乎实际且一般的捕食者—食饵系统模型应基于“比率依赖”理论。所谓“比率依赖”是指捕食者种群的平均增长率应与食饵种群密度及捕食者种群密度之比的函数有关。基于比率依赖的捕食者—食饵系统模型越来越受到数学生态学工作者的重视,在文[1]中Arditi和Ginzburg最早研究了基于比率依赖的捕食者-食饵系统模型,在文[2]中研究了基于比率依赖的具时滞的捕食者-食饵系统解的周期性,在文[3]中研究了在有时滞的情况下两种群基于比率依赖的捕食者-食饵系统的全局稳定性和持续生存的条件,而文[4]则研究了在有时滞的情况下多种群基于比率依赖的捕食者-食饵系统的全局稳定性和持续生存的条件。
(1)
一般地,种群系统所处的环境是随机变化的,环境中的许多因素都随时间的改变而随机地变化,种群系统状态也就会受到环境随机噪声的影响。因此我们必须考虑种群系统所处环境的随机性,随机微分方程理论给我们提供了随机环境下两种群捕食者-食饵系统分析的重要理论基础。文献[5]研究了随机Lotka-Volterra模型的性质,文[6]研究了环境噪声下两种群系统的稳定性和有界性,文[7]研究了在有时滞的情况下随机捕食者-食饵系统的全局正解、随机最终有界等性质,文[8]研究了在有时滞的情况下随机多种群系统的全局正解、随机最终有界和渐近稳定等性质。在文[9]中,我们研究了基于比率依赖的两种群捕食者-食饵的随机系统,得到了全局正解和解的有界性。到目前为止,还没有文献涉及到基于比率依赖的随机两种群捕食者-食饵系统解的渐近性质。
在本文中,我们运用随机微分方程的理论来讨论随机环境下基于比率依赖的两种群捕食者-食饵系统解的几个渐近性质。
1 基础知识
(2)
其中a,b,c,d,p,m为正常数,σ=(σij)2×2是随机噪声密度系数矩阵。为讨论随机干扰对种群系统的影响,假设(H1)σ11>0,σ22>0,σ12≥0,σ21≥0。 在文献[9]中,我们证明了关于模型(2)解的存在唯一性的如下定理。

在模型(2)中,若取
a=0.1,b=0.05,c=0.02,m=0.4,d=0.08,p=0.01,σ11=0.01,σ12=0.02,σ21=0.02,σ22=0.01,易验证假设条件(H1)成立,取初值x(0)=(x1(0),x2(0))=(5,5),步长Δt=0.001,x1(t)和x2(t)的轨道模拟图如图1所示。

图1 假设(H1)下模型的全局解的轨道模拟Fig.1 The pathwise of the global solution of (1) under the hypothesis (H1)
定理1和图1都说明了系统(2)中所研究生物种群受到随机环境干扰时,不论这个干扰多么小,模型(2)都不会出现爆炸解。
2 随机最终有界
在本节中,我们将讨论系统(2)的随机最终有界性质。首先我们给出随机最终有界的定义[8]:


随机最终有界说的是种群规模在大概率下低于某个值,不会发生爆发。下面给出它的证明。
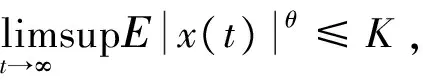
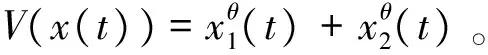
(3)
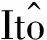
d[etV(x(t))]=etV(x(t))dt+etdV(x(t))=
[et(LV(x(t))+V(x(t)))]dt+
(4)
其中:
(5)
(6)
对每个整数n≥|x(0)|,定义停时ρn=inf{t∈R+:|x(t)|≥n},
于是有
Ε(etV(x(t∧ρn)))=V(x(0))+
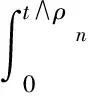
(7)
由式(6)-(7)得
etΕ(V(x(t∧ρn)))≤V(x(0))+ket
(8)
令n→∞得
etΕ(V(x(t)))≤V(x(0))+ket
两边同时除以et,得
ΕV(x(t))≤V(x(0))e-t+k
对任意的xi>0(i=1,2),有
得
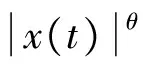
于是有
(9)
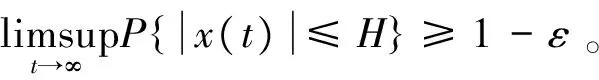
证明在引理3 中令θ=1/2,存在M>0使得
(10)
对任意的ε>0,令H=M2/ε2,则由Chebyshev不等式有
(11)
于是
即

(12)
证毕。
由引理3和定理4可称系统(2)是随机最终有界的。
3 渐近矩估计
由于无法获得解析解,渐近矩估计说明的是解的平均值(相对时间t)的变化特征。
对于模型(2),我们有关于渐近矩估计定理如下。

证明在式(3)中,容易得
(13)
(14)
(15)
由式(13)-(15)得
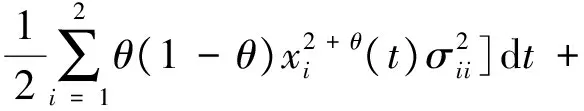
(16)
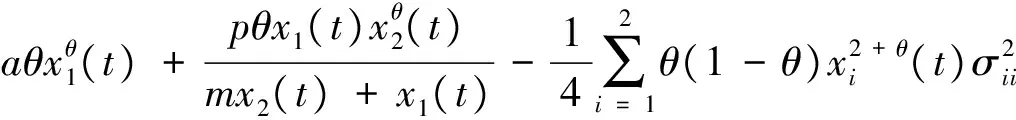

(17)
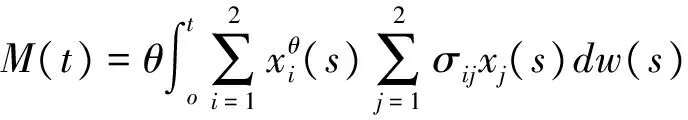
(18)
两边同时除以t得到
(19)
则有
(20)
因此得证。
4 轨道估计
由于无法获得解析解,轨道估计说明的是依概率1下,解(轨道) (相对时间t)的变化特征。对于模型(2),我们有关于轨道估计定理如下。



(21)
(22)

给定任意的ε∈(0,1)和θ>1,对于每一个正数k≥1,根据指数鞅不等式有
由Borel-Cantelli引理可知,存在Ωi⊂Ω满足P(Ωi)=1,(i=1,2)且对任意的ω∈Ωi能找到一个整数ki=ki(ω)(i=1,2)使得,对所有的0≤t≤k和k≥ki(ω)有
则方程(21)-(22)可变为


(23)

(24)
对于任意的ω∈Ωi(i=1,2),当0≤t≤k和k≥ki(ω)(i=1,2)时,式(23)-(24)可以改写成

(25)

(26)

存在正常数K,使
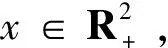
(27)
因此,对于任意给定的ω∈Ω0,如果k-1≤t≤k和k≥k0(ω)
(28)
则
(29)
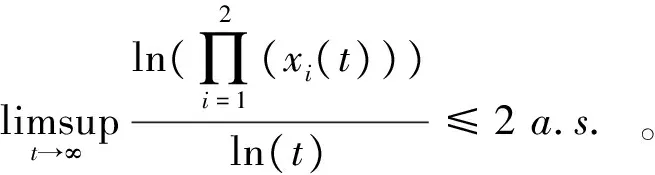
在模型(2)中,取两组值,
第一组值:a=0.08,b=0.03,c=0.02,m=0.02,d=0.03,p=0.01,σ11=0.02,σ12=0.01,σ21=0.03,σ22=0.025;
第二组值:a=0.1,b=0.05,c=0.02,m=0.4,d=0.08,p=0.01,σ11=0.01,σ12=0,σ21=0,σ22=0.01,
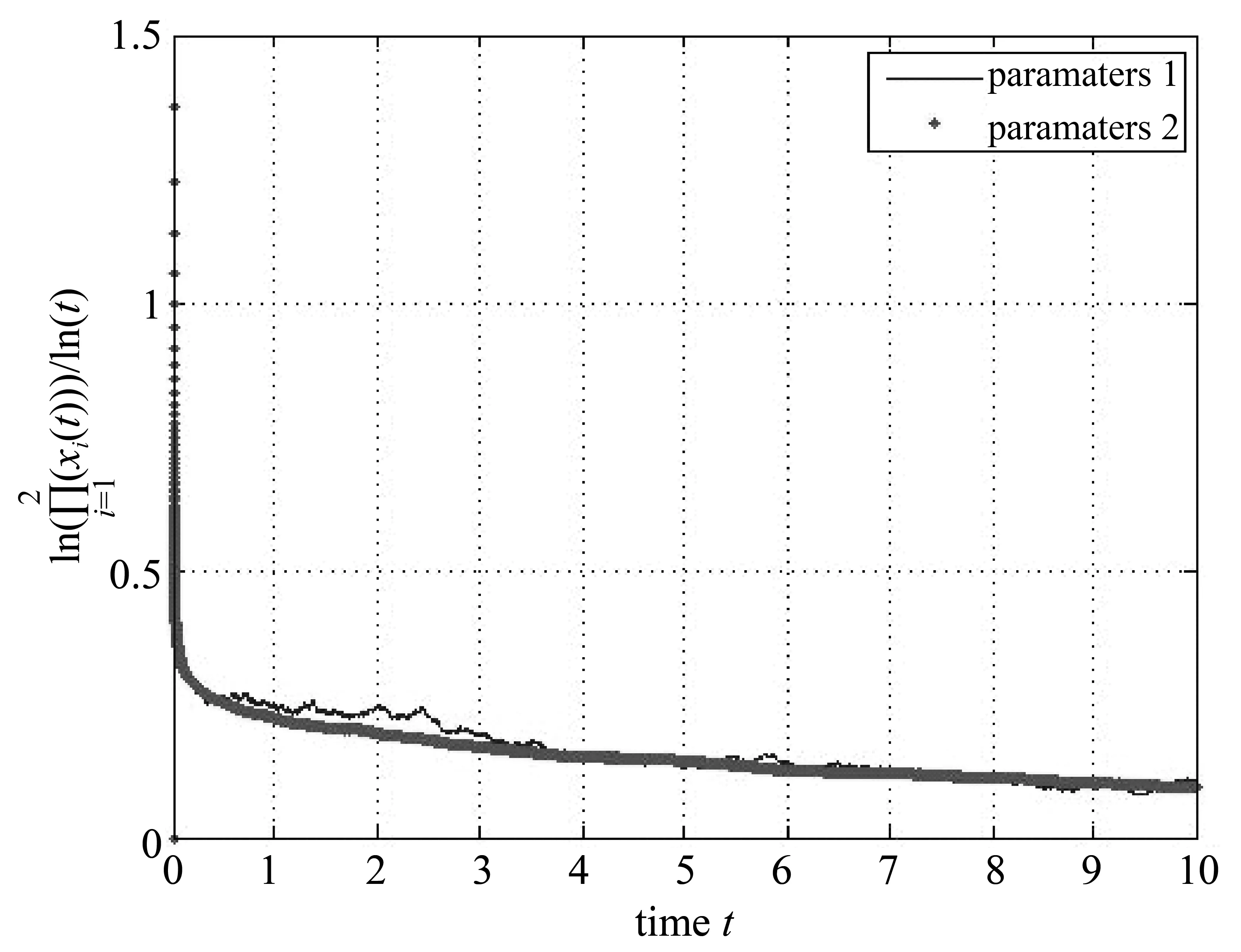
图2 假设(H1)下轨道模拟under the hypothesis (H1)
参考文献:
[1] ARDITI R, GINZBURG L R. Coupling in predator-prey dynamics: ratio-dependence[J]. Journal of Theoretical Biology, 1989, 139:311-326.
[2] FAN M, WANG K. Periodicity in a delayed ratio-dependent predator-prey system [J]. Journal of Mathematical Analysis and Applications, 2001, 262:179-190.
[3] XU R, DAVIDSON F A, CHAPLAIN M A J. Persistence and stability for a two-species ratio-dependent predator-prey system with distributed time delay [J].Journal of Mathematical Analysis and Applications,2002, 269:256-277.
[4] XU R, CHEN L S. Persistence and global stability for n-species ratio-dependent predator-prey system with time delays [J]. Journal of Mathematical Analysis and Applications, 2002, 275:27-43.
[5] MAO X R, SABANIS S, ERIC R. Asymptotic behavior of the stochastic Lotka-Volterra model [J]. Journal of Mathematical Analysis and Applications, 2003, 287:141-156.
[6] MAO X R, GLENN M, ERIC R. Environment Brownian noise suppresses explosions in population dynamics [J]. Stochasitc Processes and Their Application, 2002, 97:95-110.
[7] ARIFAH B, MAO X R. Stochastic delay Lotka-Volterra model [J]. Journal of Mathematical Analysis and Applications, 2004, 292:364-380.
[8] MAO X R, YUAN C G, ZOU J Z. Stochastic differential delay equations of population dynamics [J]. Journal of Mathematical Analysis and Applications, 2005, 304:296-320.
[9] 郭子君. 基于比率依赖的两种群捕食者-食饵系统的随机模型[J].中山大学学报:自然科学版, 2010,49(2):48-53.

