华南地气感热通量交换系数的估算*

彭玉麟，何春燕，2，简茂球

(1. 中山大学环境科学与工程学院大气科学系/季风与环境研究中心，广东 广州 510275；2.东莞市气象局，广东 东莞 523086)

气候变化是当今社会人们关注的热点问题。气候变化与气候系统中各圈层之间的相互作用密切相关，而各圈层之间的相互作用中，陆气相互作用扮演着重要的角色。在陆气相互作用中，主要有感热通量交换和潜热通量交换。如果我们根据由整体法得到的参数化公式(见(1)式)来计算感热通量，必然要先确定感热交换系数Ch的数值大小。该参数数值的确定对大气数值模拟和陆面过程参数化具有重要的应用参考价值。

我国对于陆气通量观测的研究，主要有1988-1992年的“黑河地区地气相互作用野外观测实验研究”(简称HEIFE)，期间的研究成果如胡隐樵等[1]发现干旱地区地表热量平衡以感热为主，潜热可以忽略不计，能量和湍流的参数化必须考虑层结的影响。左洪超等[2]对黑河试验区沙漠和戈壁的总体输送系数进行研究，发现沙漠和戈壁的中性总体输送系数分别为2.2×10-3和1.6×10-3，随风速无明显变化，并且求得总体输送系数与总体Richardson数和粗糙度的拟合关系式。从2000年5月开始，在甘肃和青海两省展开了“西北干旱区陆-气相互作用野外观测试验”(简称NWC-ALIEX)，张强等[3-5]利用NWC-ALIEX资料做了一系列的研究，如用三种方法确定了干旱荒漠戈壁区动量和感热总体输送系数，得出典型干旱荒漠戈壁区动量和感热总体输送系数与总体Richardson数的关系和典型值范围[3]；韦志刚等[6]利用空气动力学法计算分析了敦煌戈壁2000年9月-2001年9月的感热交换系数变化特征，讨论其在不同近地层大气稳定度下的变化及其与风速的关系，得到近似的拟合关系式。除了在西北地区的观测试验，闫俊岳等[7]利用南海海气通量观测试验资料，分析了南海西南季风爆发前后海气通量交换系数的差异。邓雪娇等[8]在广州番禺开展了陆气相互作用的观测研究，获取了代表珠三角地区冲积扇平原草地的陆气相互作用过程基础资料，发现涡动相关法计算的感热通量和潜热通量之和(Qh+Qe)普遍偏小,与可用能量净辐射与土壤热通量之差(Rn-Qg)在多数情况下存在能量不平衡特征，番禺夏、秋季近地层各能量具有与太阳辐射相似的日变化特征，但夏季的潜热大于感热，而秋季则相反。

前人研究表明，对于感热交换系数的研究大多集中于西北干旱区，对华南湿润区的感热交换系数的估算和研究少有涉及。基于该地区水源充沛，地气相互作用强烈，地气通量的变化会引起该地区的气候变化，因此有必要对该地区的地气通量特点进行研究，而感热交换系数的特征在其中起着重要的作用。因此，本文利用2009年东莞市气象台的涡动能量平衡系统的观测资料以及常规观测资料，从不同的角度对感热交换系数进行估算，为数值模拟提供华南区域有关参数。

1 资料和方法

本文所用的资料包括：① 东莞市气象台涡动能量平衡系统观测的2009年逐时地气感热通量资料。观测地点位于广东省东莞市植物园的观测场(113°44′E, 22°58′N,海拔56 m)，周围地势开阔，无任何高大建筑物遮蔽，附近主要的下垫面是常绿乔木、灌木及大片的草地等。观测系统安装于距地4 m高处，由CR3000数据采集器、CSAT3超声风速仪(Campbell，USA) 、LI-7500开路式CO2/H2O气体分析仪(Li-Cor，USA)和一个1G的PC卡组成。系统采集并存储30 min平均的CO2通量(Fc)、潜热通量(LE)与感热通量(SH)和原始高频时间系列数据。本研究所用的SH资料是经过处理的1 h平均数据，在剔除受降水影响出现误差的数据后，共有7 700个样本。② 2009年东莞气象站逐时观测的常规地面气象数据，包括近近地面气温、10 m风速和地表温度。

感热交换系数的估算主要根据计算感热通量的经验公式[9]：

SH=ChCpρV(Ts-Ta)=Ch·NCSH

(1)

NCSH=CpρV(Ts-Ta)

(2)

其中，SH为地表感热通量；Cp是空气的定压比热常数(1 004.67 J/(kg·K))；ρ是近地面空气密度，取东莞市的年平均值1.158 kg/m3；Ch是地气感热交换系数；V是近地面10 m 风速；Ts为地面0 cm 土壤温度；Ta是近地面1.5 m气温。

通过(1)式，利用一元线性回归方法和实际观测的感热通量SH，近地面10 m 风速V，地面0 cm土壤温度Ts和近地面1.5 m气温Ta，便可计算出来的回归系数，即为感热交换系数Ch。

以往对感热交换系数的研究大多会涉及到层结稳定度对其的影响[1-8]。本文一个主要的目的是为了估算出一个合理的感热交换系数，以便根据由整体法得到的参数化公式，利用气象测站的常规观测资料来计算长时间序列的感热通量。由于大多数台站缺少用于判别层结稳定度的观测资料，即便估算了不同层结稳定度下面的感热交换系数，也不可能在估算长时间序列的感热通量中使用，因此本文并没有涉及层结稳定度对感热交换系数的影响。

2 不同方案的感热交换系数的估算

2.1 基于全年资料的感热交换系数的估算

如果要利用尽可能多的数据样本，最简单的做法是用2009年全年的所有资料来估算出一个感热交换系数。结果如图1所示，x轴为公式(1)等号右边除感热交换系数Ch外的各项乘积(NCSH)的值，y轴为实测的感热通量，其一元线性回归方程的系数是Ch。

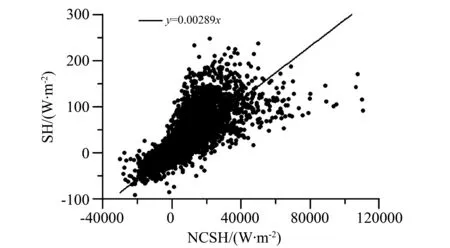
图1 基于2009年全年资料的SH和NCSH的散点图(直线是一元线性回归线)Fig.1 Scatter plots of SH and NCSH based on all the data in 2009

由图1可知，利用全年资料估算出的感热交换系数Ch为0.002 89。尽管这种方法增加了样本数，提高了估算的感热交换系数值的可信度，但是以这种方式得到的感热交换系数忽略了它的逐月差异，因此在实际估算感热通量的时候不能很好地反映它的季节变化。

2.2 不同月份的感热交换系数的估算

针对上一小节的估算结果的不足，下面同样根据公式(1)，用一元回归方法估算逐月的感热交换系数Ch，结果如图2所示。

从图2可看出，感热交换系数Ch的值具有明显的季节变化。4月感热交换系数的值最大，2月的最小；春季的感热交换系数相对较大，而夏、秋两季的感热交换系数则相对较小。按月分别估算感热交换系数后，体现了感热交换系数的逐月变化，在实际应用中能更好地反映感热通量的逐月变化。

图2 感热交换系数Ch的逐月变化Fig.2 The monthly variation in Ch

2.3 不同风速等级的感热交换系数的估算

文献[6-7]研究表明，风速的大小对感热交换系数有一定的影响，文献[10]认为改变公式(1)的风速幂指数，会对感热通量的估算有一定的改善。为此下面将根据不同的风速等级来估算感热交换系数。

根据2009年东莞站的观测资料，风速大部分分布在0～8 m/s，下面的分析把风速分成4个等级，分别是0～2、2～4、4～6和大于6 m/s，然后利用一元回归分析方法估算各等级的感热交换系数。

由图3可以看出，在不同的风速条件下，感热交换系数值是有差别的。风速在0～2 m/s的时候感热交换系数为0.004 88，风速在2～4 m/s时为0.003 45，4～6 m/s时为0.002 25，大于6 m/s时为0.001 54。由此可以看出，风速越大的时候，感热通量交换系数就越小。这与文献[6-7]分别在敦煌戈壁和南海地区研究风速与感热交换系数之间的关系所得结果一致。

对比前两小节的做法，上述分风速对感热交换系数进行估算，引入了风速的影响，如果在这基础上考虑感热交换系数的逐月变化，应该能对感热交换系数进行更为细致的描述。由于资料有限，如果对逐月的数据分风速对感热交换系数进行订正，各风速等级的样本数会偏少(特别是风速大于6 m/s时)，这样会影响到结果的可信度，因此下面我们分季节和分风速等级对感热交换系数进行估算，这样既考虑了感热交换系数的季节变化和风速对其的影响，又增加了样本数，使得估算的结果较合理也可信。

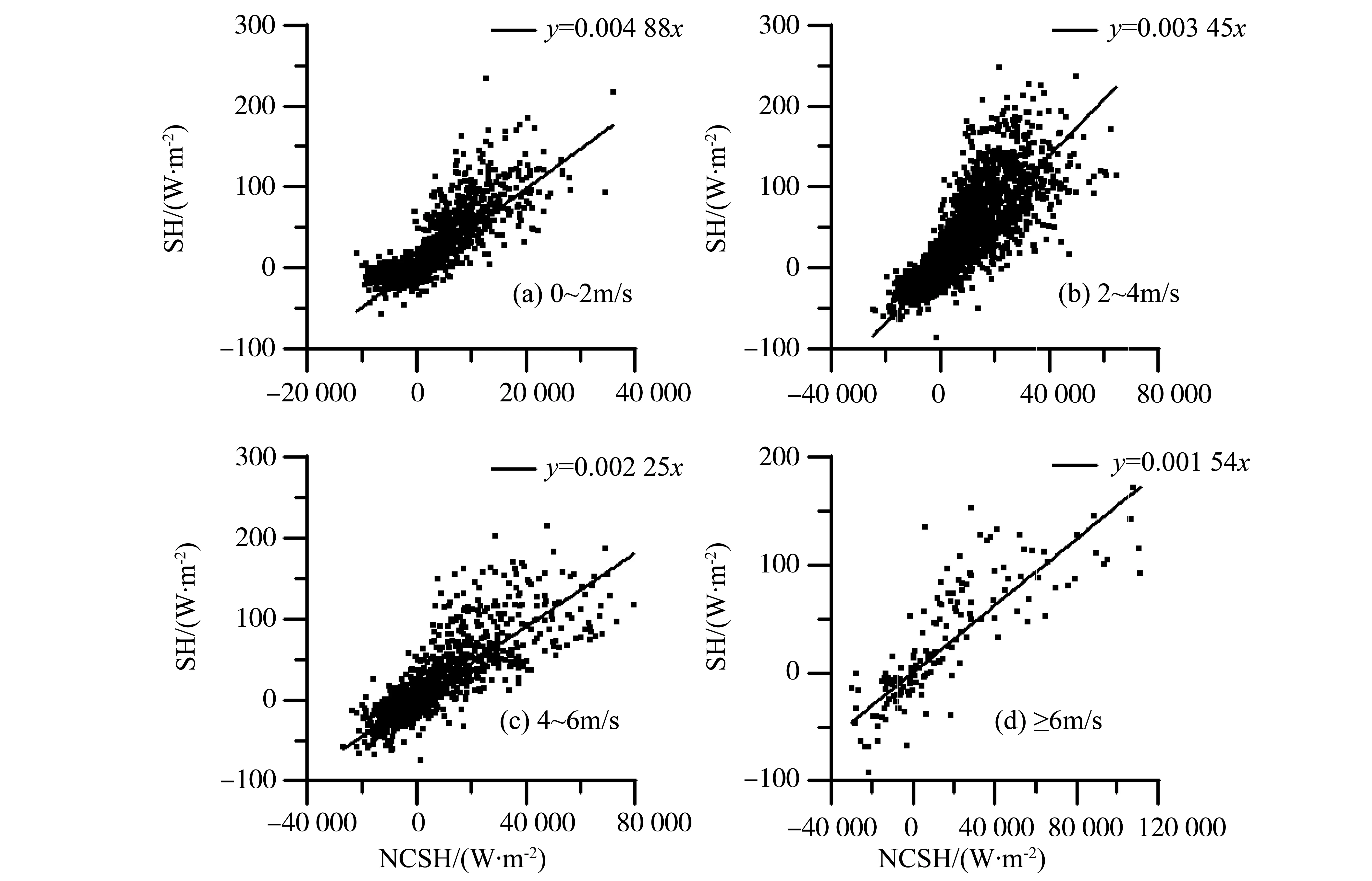
图3 不同风速条件下的SH和NCSH的散点图(直线是一元线性回归线)Fig.3 Scatter plots of SH and NCSH for different ranges of wind speed

2.4 分季节和风速等级的感热交换系数估算

分别对春季(3-5月)，夏季(6-8月)，秋季(9-11月)和冬季(12-2月)的样本按上述的风速分类，利用一元回归分析方法得出各季节各风速段的感热通量交换系数如表1所给。

表1 各季节各风速段的感热交换系数Ch1)Table 1 Ch in each range of wind velocity and season 10-3

1)Ch的年平均值为3.26×10-3,其标准差为1.55×10-3

由表1可知，在各个季节均呈现出随着风速的增大，感热交换系数值逐渐减小的特征。对比全年算出的结果，在春季，各风速段定出来的系数均要比全年的要大；在夏季，低风速段(0～2 m/s)和高风速段(≥6 m/s)的系数要比全年的要大，中间风速段的系数比全年的系数要小；秋季，除了4～6 m/s段的感热交换系数比全年的结果略大以外，其余的感热交换系数均比全年的系数要小；在冬季，除了2～4 m/s段的感热交换系数比全年的系数略大以外，其余的感热交换系数均比全年的结果要小。表1得到的感热交换系数的年平均值为3.26×10-3，比用全年所有资料估算的交换系数值2.89×10-3要大一些(见2.1小节)，其标准差为1.55×10-3。

以上根据了四种不同的方案对感热交换系数值进行了估算，在实际应用的时候，可以根据实际的情况需要，采取相应的感热交换系数值对感热通量进行估算。需指出的是，上述对感热交换系数的各种估算值都通过95%的信度检验(按一元线性回归方程的检验做)。

4 总结与讨论

本文利用了东莞市气象台2009年的涡动能量观测数据和常规观测数据，采取全年、分月、分风速等级和分季节风速等级4种方案估算感热交换系数值，结果表明：

1)感热交换系数具有明显的季节变化。在4月份达到峰值，2月份达到谷值。春季的感热通量交换系数相对较大，而夏、秋两季的感热交换系数则相对较小。

2)风速对感热交换系数值的影响是：风速越大，感热交换系数的值越小。

3)分季节及风速估算出的感热交换系数的平均值为3.26×10-3，其标准差为1.55×10-3。

由于东莞位于华南地区，所以本文估算的感热交换系数可有条件地应用到华南地区。虽然本文只用了一年的数据资料来估算，但是由于用的数据资料是逐时的，有7 700个样本可以说这些样本代表了足够多的不同天气背景(雨天除外)，因此，本文估算的结果是具有较好的代表性和可信度的。尽管如此，据此确定出来的感热交换系数的适用程度还有待更多观测资料的验证。此外，收集不同地区和更长时间跨度的地气通量观测资料，也可以更好地验证估算的感热交换系数在华南地区的适用性。

参考文献：

[1] 胡隐樵, 高由禧. 黑河试验(HEIFE) ——对干旱地区陆面过程的一些新认识[J]. 气象学报,1994,52(3): 285-296.

[2] 左洪超,胡隐樵.黑河试验区沙漠和戈壁的总体输送系数[J].高原气象,1992,11(4): 371-380

[3] 张强,卫国安,黄荣辉. 西北干旱区荒漠戈壁动量和感热总体输送系数[J]. 中国科学:D辑,2001,31(9): 783-792.

[4] ZHANG Q, HUANG R H, TIAN H. A Parameterization scheme of surface turbulent momentum and sensible heat over the gobi underlying surface [J]. Adv Atmos Sci, 2003, 20(1): 111-118.

[5] 张强,卫国安.荒漠戈壁大气总体曳力系数和输送系数观测研究[J]. 高原气象, 2004, 23(3): 305-312.

[6] 韦志刚，黄荣辉，陈文. 敦煌戈壁不同近地层大气稳定度下的感热交换系数[J]. 高原气象，2006，25(5)：834-839.

[7] 闫俊岳,唐志毅,姚华栋，等. 南海西南季风爆发前后海-气通量交换系数研究[J]. 气象学报，2006，64(3)：335-344.

[8] 邓雪娇,毕雪岩,吴兑,等. 广州番禺地区草地陆气相互作用观测研究[J]. 应用气象学报,2006,17 (1) :59-66.

[9] 周连童,黄荣辉.中国西北干旱、半干旱区感热的年代际变化特征及其与中国夏季降水的关系[J]. 大气科学, 2008, 32 (6) : 1276-1288.

[10] 何春燕. 2009年东莞地气通量观测研究[D]. 广州：中山大学，2010:29-31.